Introdução aos números complexos

Se eu precisasse descrever a distância entre duas cidades, poderia fornecer uma resposta consistindo em um único número em milhas, quilômetros ou alguma outra unidade de medida linear.

No entanto, se eu fosse descrever como viajar de uma cidade para outra, teria que fornecer mais informações do que apenas a distância entre essas duas cidades; Eu também teria que fornecer informações sobre a direção para viajar também.

O tipo de informação que expressa uma única dimensão, como distância linear, é chamado de escalar quantidade em matemática. Os números escalares são o tipo de número que você usou na maioria de todas as suas aplicações matemáticas até agora.

A tensão produzida por uma bateria, por exemplo, é uma grandeza escalar. O mesmo ocorre com a resistência de um pedaço de fio (ohms) ou a corrente que passa por ele (amperes).

No entanto, quando começamos a analisar circuitos AC, encontramos essa quantidade de tensão, corrente e até mesmo resistência (chamada de impedância em AC) não são as quantidades unidimensionais familiares que estamos acostumados a medir em circuitos DC.

Em vez disso, essas quantidades, por serem dinâmicas (alternando em direção e amplitude), possuem outras dimensões que devem ser levadas em consideração. Freqüência e mudança de fase são duas dessas dimensões que entram em jogo.

Mesmo com circuitos CA relativamente simples, onde lidamos apenas com uma única frequência, ainda temos a dimensão da mudança de fase para enfrentar, além da amplitude.

Para analisar com sucesso os circuitos AC, precisamos trabalhar com objetos matemáticos e técnicas capazes de representar essas grandezas multidimensionais.

É aqui que precisamos abandonar os números escalares por algo mais adequado: números complexos . Assim como o exemplo de dar direções de uma cidade para outra, as grandezas CA em um circuito de frequência única têm amplitude (analogia:distância) e mudança de fase (analogia:direção).

Um número complexo é uma quantidade matemática única capaz de expressar essas duas dimensões de amplitude e mudança de fase ao mesmo tempo.

Representação gráfica de números complexos

Os números complexos são mais fáceis de entender quando são representados graficamente. Se eu desenhar uma linha com um certo comprimento (magnitude) e ângulo (direção), tenho uma representação gráfica de um número complexo que é comumente conhecido na física como um vetor :(Figura abaixo)







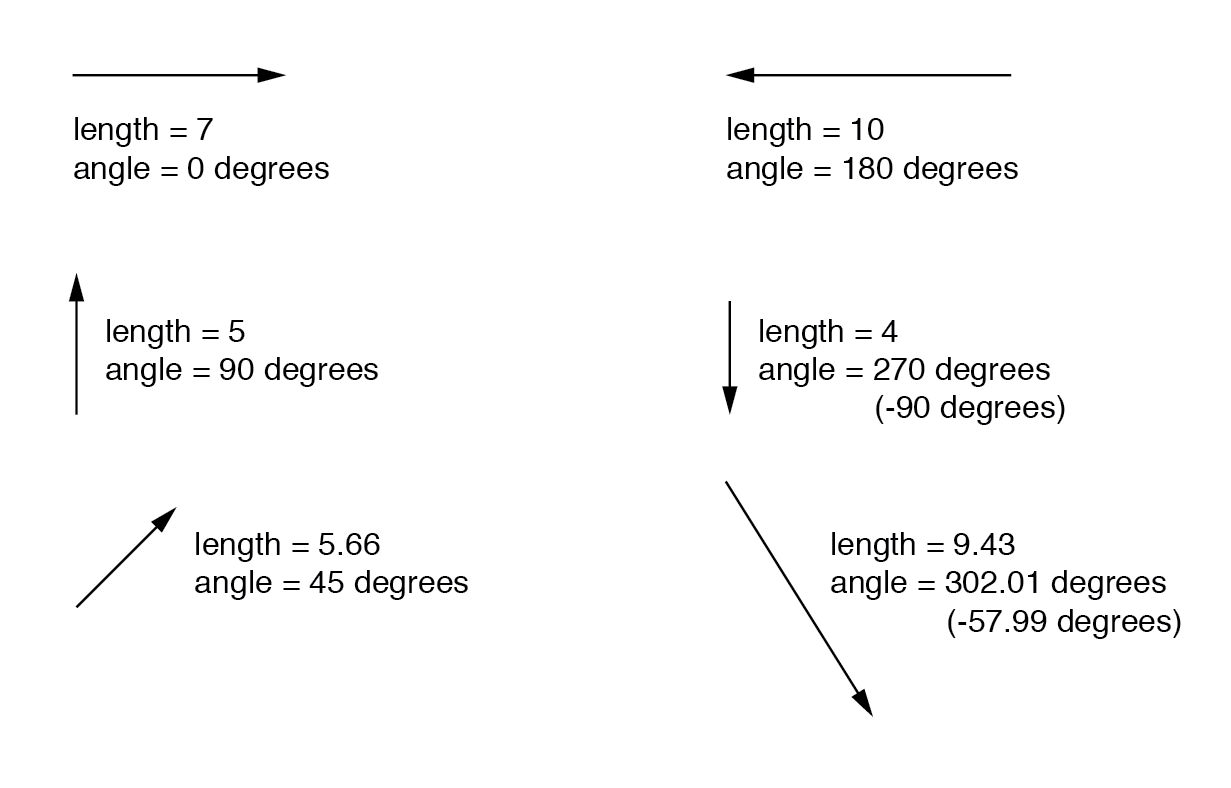
Como distâncias e direções em um mapa, deve haver algum referencial comum para que as figuras angulares tenham algum significado. Neste caso, diretamente correto é considerado 0 ^o , e os ângulos são contados em uma direção positiva indo no sentido anti-horário:(Figura abaixo)







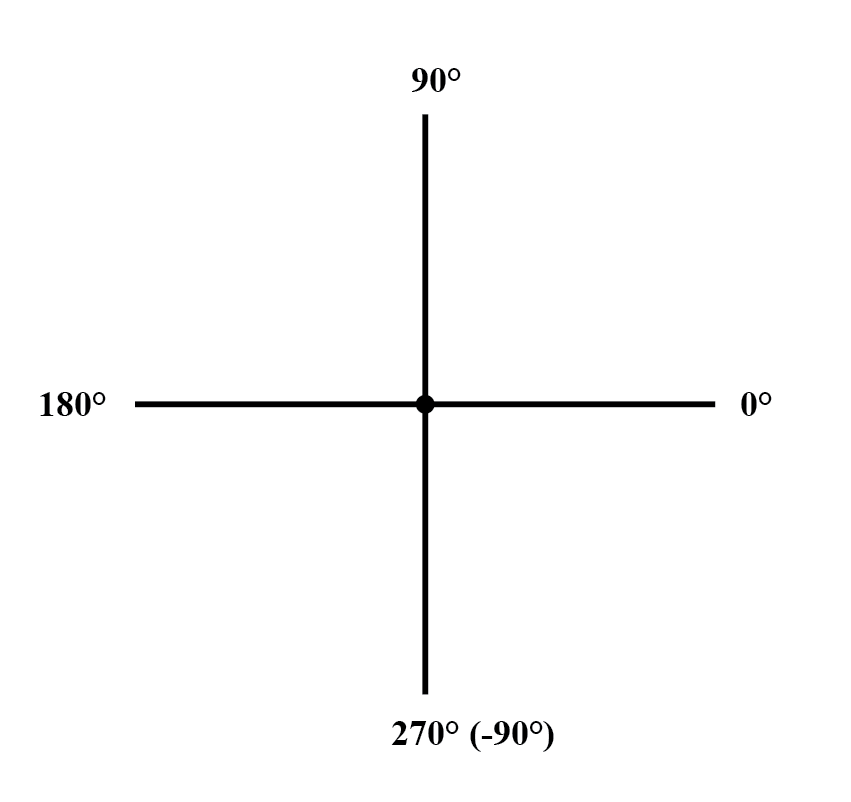
A ideia de representar um número na forma gráfica não é nova. Todos nós aprendemos isso na escola primária com a “linha numérica:” (Figura abaixo)







Aprendemos até como a adição e a subtração funcionam ao ver como os comprimentos (magnitudes) se acumulam para dar uma resposta final:(Figura abaixo)







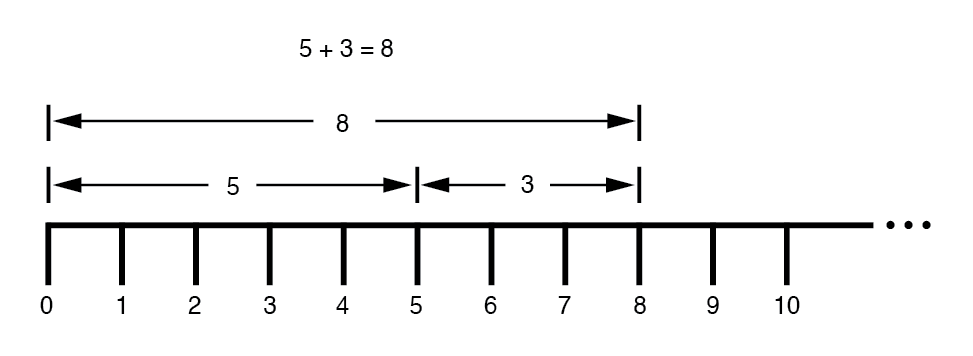
Mais tarde, aprendemos que havia maneiras de designar os valores entre os números inteiros marcados na linha. Estas eram quantidades fracionárias ou decimais:(Figura abaixo)







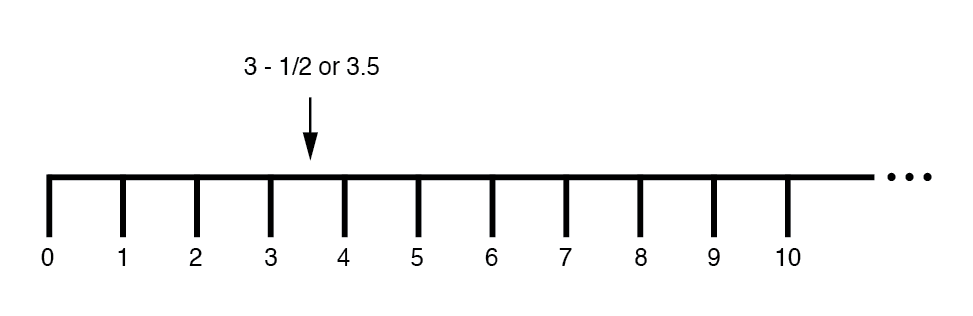
Esses campos de números (inteiro, inteiro, racional, irracional, real, etc.) aprendidos na escola primária compartilham uma característica comum:eles são todos unidimensionais . A retidão da reta numérica ilustra isso graficamente.

Você pode mover para cima ou para baixo na linha numérica, mas todo “movimento” ao longo dessa linha é restrito a um único eixo (horizontal).

Os números escalares unidimensionais são perfeitamente adequados para contar contas, representar peso ou medir a tensão da bateria DC, mas não conseguem representar algo mais complexo como a distância e direção entre duas cidades, ou a amplitude e fase de uma forma de onda AC.

Para representar esses tipos de quantidades, precisamos de representações multidimensionais. Em outras palavras, precisamos de uma reta numérica que pode apontar em diferentes direções, e isso é exatamente o que um vetor é.



REVER:

• Um escalar número é o tipo de objeto matemático que as pessoas estão acostumadas a usar na vida cotidiana:uma quantidade unidimensional como temperatura, comprimento, peso etc.
• Um número complexo é uma quantidade matemática que representa duas dimensões de magnitude e direção.
• Um vetor é uma representação gráfica de um número complexo. Parece uma seta, com um ponto de partida, uma ponta, um comprimento definido e uma direção definida. Às vezes, a palavra fasor é usado em aplicações elétricas onde o ângulo do vetor representa a mudança de fase entre as formas de onda.

PLANILHA RELACIONADA:

• Planilha da fase AC