Circuitos resistor-capacitor série

Na última seção, aprendemos o que aconteceria em circuitos CA simples apenas com resistor e apenas com capacitor. Agora vamos combinar os dois componentes em série e investigar os efeitos.

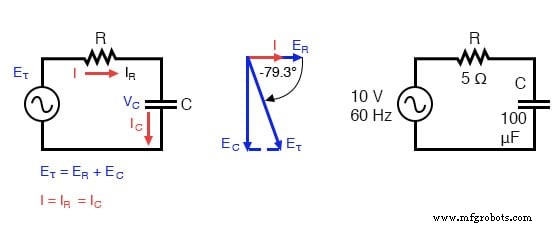
Circuito do capacitor em série:a tensão atrasa a corrente de 0 ° a 90 °.

Cálculo da impedância

O resistor oferecerá 5 Ω de resistência à corrente CA independentemente da frequência, enquanto o capacitor oferecerá 26,5258 Ω de reatância à corrente CA a 60 Hz.

Como a resistência do resistor é um número real (5 Ω ∠ 0 °, ou 5 + j0 Ω), e a reatância do capacitor é um número imaginário (26,5258 Ω ∠ -90 ° ou 0 - j26,5258 Ω), o efeito combinado dos dois componentes será uma oposição à corrente igual à soma complexa dos dois números.

O termo para esta oposição complexa à corrente é impedância , seu símbolo é Z, e também é expresso na unidade de ohms, assim como resistência e reatância. No exemplo acima, a impedância total do circuito é:







A impedância está relacionada à tensão e corrente, assim como você pode esperar, de uma maneira semelhante à resistência na Lei de Ohm:







Na verdade, esta é uma forma muito mais abrangente da Lei de Ohm do que o que foi ensinado na eletrônica DC (E =IR), assim como a impedância é uma expressão muito mais abrangente de oposição ao fluxo de elétrons do que a simples resistência. Qualquer resistência e qualquer reatância, separadamente ou em combinação (série / paralelo), pode e deve ser representada como uma única impedância.

Cálculo Atual

Para calcular a corrente no circuito acima, primeiro precisamos fornecer uma referência de ângulo de fase para a fonte de tensão, que geralmente é considerada zero. (Os ângulos de fase de impedância resistiva e capacitiva são sempre 0 ° e -90 °, respectivamente, independentemente dos ângulos de fase fornecidos para tensão ou corrente.)











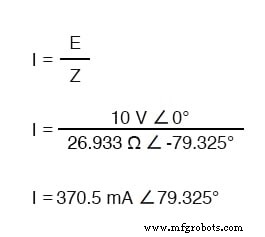
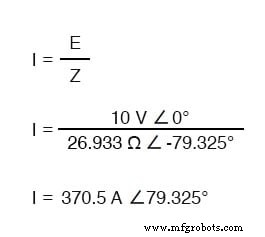
Como acontece com o circuito puramente capacitivo, a onda de corrente está liderando a onda de tensão (da fonte), embora desta vez a diferença seja 79,325 ° em vez de 90 ° completos.

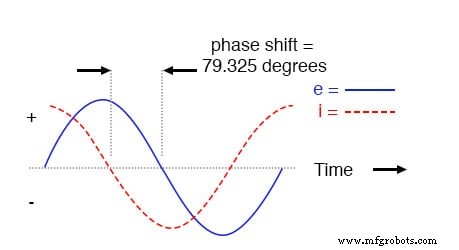
A tensão atrasa a corrente (tensão dos fios da corrente) em um circuito em série R-C.

Método da tabela

Como aprendemos no capítulo sobre indutância CA, o método de “tabela” para organizar as grandezas do circuito é uma ferramenta muito útil para análise CA assim como é para análise CC. Vamos colocar os números conhecidos para este circuito em série em uma tabela e continuar a análise usando esta ferramenta:







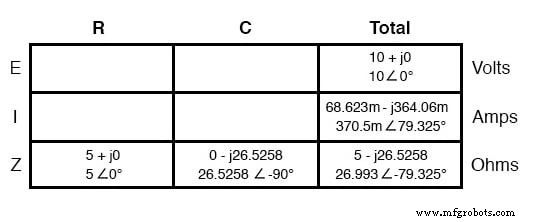
A corrente em um circuito em série é compartilhada igualmente por todos os componentes, de modo que os valores colocados na coluna "Total" para a corrente também podem ser distribuídos para todas as outras colunas:

Continuando com nossa análise, podemos aplicar a Lei de Ohm (E =IR) verticalmente para determinar a tensão através do resistor e capacitor:







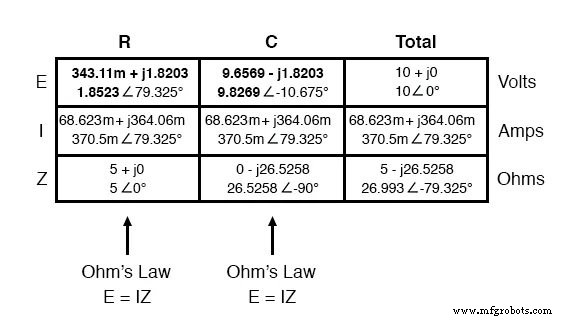
Observe como a tensão através do resistor tem exatamente o mesmo ângulo de fase que a corrente através dele, nos dizendo que E e I estão em fase (apenas para o resistor). A tensão através do capacitor tem um ângulo de fase de -10,675 °, exatamente 90 ° menos do que o ângulo de fase da corrente do circuito. Isso nos diz que a tensão e a corrente do capacitor ainda estão 90 ° defasadas uma com a outra.

Cálculos usando SPICE

Vamos verificar nossos cálculos com SPICE:

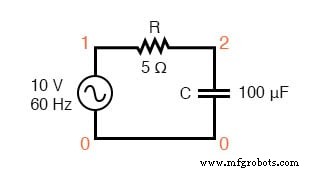
Circuito de especiarias:R-C.


circuito

 ac r-c v1 1 0 ac 10 sin r1 1 2 5 c1 2 0 100u .ac lin 1 60 60 .print ac v (1,2) v (2,0) i (v1) .print ac vp (1,2) vp (2,0) ip (v1) .fim freq v (1,2) v (2) i (v1) 6,000E + 01 1,852E + 00 9,827E + 00 3,705E-01 freq vp (1,2) vp (2) ip (v1) 6,000E + 01 7,933E + 01 -1,067E + 01 -1,007E + 02 

Mais uma vez, o SPICE imprime de forma confusa o ângulo de fase atual em um valor igual ao ângulo de fase real mais 180 ° (ou menos 180 °).

No entanto, é simples corrigir esse número e verificar se nosso trabalho está correto. Nesse caso, a saída de -100,7 ° do SPICE para o ângulo de fase atual equivale a 79,3 ° positivo, o que corresponde à nossa figura calculada anteriormente de 79,325 °.

Novamente, deve ser enfatizado que os números calculados correspondentes às medições de tensão e corrente da vida real são aqueles em polar forma, não forma retangular!

Por exemplo, se fossemos realmente construir este circuito resistor-capacitor em série e medir a tensão através do resistor, nosso voltímetro indicaria 1,8523 volts, não 343,11 milivolts (retangular real) ou 1,8203 volts (retangular imaginário).

Instrumentos reais conectados a circuitos reais fornecem indicações correspondentes ao comprimento do vetor (magnitude) das figuras calculadas. Embora a forma retangular da notação numérica complexa seja útil para realizar adição e subtração, é uma forma mais abstrata de notação do que a polar, que por si só tem correspondência direta com medidas verdadeiras.

A impedância (Z) de um circuito em série R-C pode ser calculada, dada a resistência (R) e a reatância capacitiva (X _C ) Uma vez que E =IR, E =IX _C e E =IZ, resistência, reatância e impedância são proporcionais à tensão, respectivamente. Assim, o diagrama fasorial de tensão pode ser substituído por um diagrama de impedância semelhante.

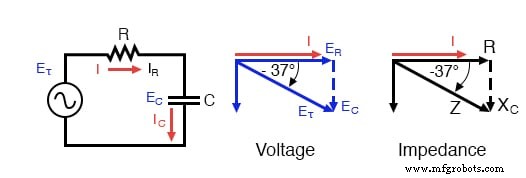
Série:diagrama fasorial da impedância do circuito R-C.



Exemplo: Dado:Um resistor de 40 Ω em série com um capacitor de 88,42 microfarad. Encontre a impedância em 60 hertz.

 XC =1 / (2πfC) XC =1 / (2π · 60 · 88,42 × 10-6) XC =30 Ω Z =R - jXC Z =40 - j30 | Z | =sqrt (402 + (-30) 2) =50 Ω ∠Z =arco tangente (-30/40) =-36,87 ° Z =40 - j30 =50∠-36,87 ° 

REVER:

• Impedância é a medida total de oposição à corrente elétrica e é a soma complexa (vetorial) da resistência ("real") e reatância ("imaginária").
• As impedâncias (Z) são gerenciadas da mesma forma que as resistências (R) na análise de circuitos em série:as impedâncias em série são adicionadas para formar a impedância total. Apenas certifique-se de realizar todos os cálculos de forma complexa (não escalar)! Z _Total1 + Z ₂ +. . . Z _n
• Observe que as impedâncias sempre são adicionadas em série, independentemente do tipo de componentes que as compõem. Ou seja, impedância resistiva, impedância indutiva e impedância capacitiva devem ser tratadas da mesma forma matematicamente.
• Uma impedância puramente resistiva sempre terá um ângulo de fase de exatamente 0 ° (Z _R =R Ω ∠ 0 °).
• Uma impedância puramente capacitiva sempre terá um ângulo de fase de exatamente -90 ° (Z _C =X _C Ω ∠ -90 °).
• Lei de Ohm para circuitos AC:E =IZ; I =E / Z; Z =E / I
• Quando resistores e capacitores são misturados em circuitos, a impedância total terá um ângulo de fase em algum lugar entre 0 ° - e -90 °.

PLANILHAS RELACIONADAS:

• Planilha de circuitos CA série e paralela