Sinais de onda quadrada

Foi descoberto que qualquer a forma de onda repetitiva não senoidal pode ser equiparada a uma combinação de tensão DC, ondas senoidais e / ou ondas cosseno (ondas senoidais com uma mudança de fase de 90 graus) em várias amplitudes e frequências.

Isso é verdade, não importa o quão estranha ou complicada a forma de onda em questão possa ser. Desde que se repita regularmente ao longo do tempo, é redutível a esta série de ondas sinusoidais.

Em particular, foi descoberto que as ondas quadradas são matematicamente equivalentes à soma de uma onda senoidal na mesma frequência, mais uma série infinita de ondas senoidais de frequência múltipla ímpar em amplitude decrescente:







A princípio, essa verdade sobre as formas de onda pode parecer estranha demais para acreditar. No entanto, se uma onda quadrada é na verdade uma série infinita de harmônicos de onda senoidal somados, é lógico que deveríamos ser capazes de provar isso somando vários harmônicos de onda senoidal para produzir uma grande aproximação de uma onda quadrada.

Este raciocínio não é apenas sólido, mas facilmente demonstrado com SPICE.

O circuito que vamos simular nada mais é do que várias fontes de tensão CA de onda senoidal com amplitudes e frequências adequadas conectadas em série. Usaremos SPICE para plotar as formas de onda de tensão em adições sucessivas de fontes de tensão, como esta:

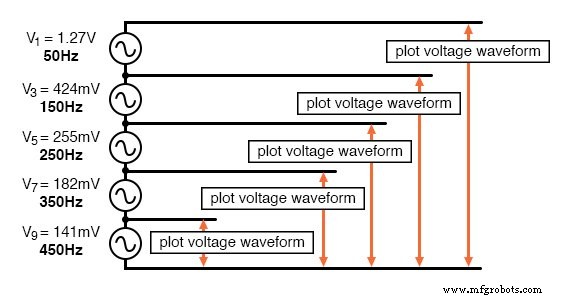
Uma onda quadrada é aproximada pela soma dos harmônicos.



Nesta simulação SPICE específica, eu somei a 1ª, 3ª, 5ª, 7ª e 9ª fontes de tensão harmônica em série para um total de cinco fontes de tensão CA. A frequência fundamental é 50 Hz e cada harmônico é, obviamente, um múltiplo inteiro dessa frequência.

Os valores de amplitude (voltagem) não são números aleatórios; em vez disso, eles foram obtidos por meio das equações mostradas na série de frequência (a fração 4 / π multiplicada por 1, 1/3, 1/5, 1/7, etc. para cada um dos harmônicos ímpares crescentes).

 construindo uma onda quadrada v1 1 0 sin (0 1.27324 50 0 0) 1º harmônico (50 Hz) v3 2 1 sin (0 424,413m 150 0 0) 3º harmônico v5 3 2 sin (0 254.648m 250 0 0) 5º harmônico v7 4 3 sin (0 181.891m 350 0 0) 7º harmônico v9 5 4 sin (0 141,471m 450 0 0) 9º harmônico r1 5 0 10k .tran 1m 20m .plot tran v (1,0) Plotagem do 1º harmônico .plot tran v (2,0) Plotando 1º + 3º harmônicos .plot tran v (3,0) Plotagem 1º + 3º + 5º harmônicos . traçar tran v (4,0) Traçar 1o + 3o + 5o + 7o harmônicos .plot tran v (5,0) Plot 1st +. . . + 9º harmônico .fim 

Vou narrar a análise passo a passo a partir daqui, explicando o que estamos vendo. Neste primeiro gráfico, vemos a onda senoidal de frequência fundamental de 50 Hz sozinha. Não é nada além de uma forma senoidal pura, sem conteúdo harmônico adicional. Este é o tipo de forma de onda produzida por uma fonte de alimentação CA ideal:

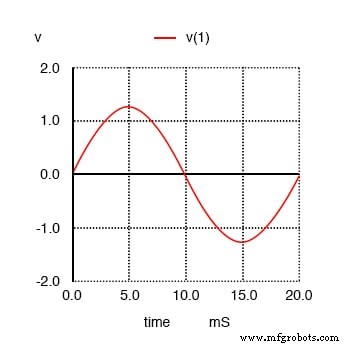
Onda senoidal pura de 50 Hz.



A seguir, vemos o que acontece quando essa forma de onda simples e limpa é combinada com o terceiro harmônico (três vezes 50 Hz ou 150 Hz). De repente, não parece mais uma onda senoidal limpa:

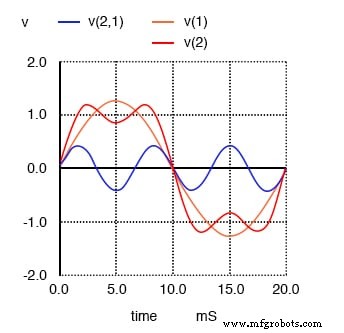
A soma da 1ª (50 Hz) e da 3ª (150 Hz) harmônicas se aproxima de uma onda quadrada de 50 Hz.



Os tempos de subida e descida entre os ciclos positivos e negativos são muito mais íngremes agora, e as cristas da onda estão mais perto de se tornarem planas como uma onda quadrada. Observe o que acontece à medida que adicionamos a próxima frequência harmônica ímpar:

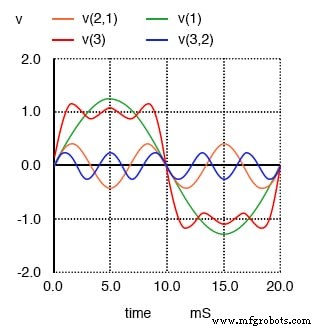
Soma do 1º, 3º e 5º harmônicos aproxima a onda quadrada.



A mudança mais notável aqui é como as cristas da onda se achataram ainda mais. Existem mais depressões e cristas em cada extremidade da onda, mas essas depressões e cristas são menores em amplitude do que eram antes. Observe novamente enquanto adicionamos a próxima forma de onda harmônica ímpar à mistura:

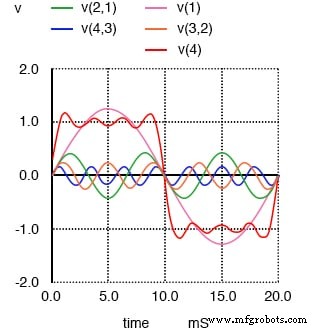
Soma da 1ª, 3ª, 5ª e 7ª harmônicas aproxima a onda quadrada.



Aqui podemos ver a onda ficando mais achatada a cada pico. Finalmente, adicionando o 9º harmônico, a quinta fonte de tensão de onda senoidal em nosso circuito, obtemos este resultado:

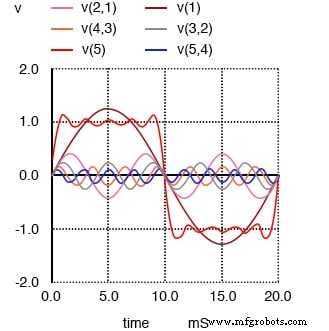
Soma da 1ª, 3ª, 5ª, 7ª e 9ª harmônicas aproxima a onda quadrada.



O resultado final da adição das primeiras cinco formas de onda harmônicas ímpares (todas nas amplitudes adequadas, é claro) é uma grande aproximação de uma onda quadrada. O objetivo ao fazer isso é ilustrar como podemos construir uma onda quadrada a partir de várias ondas senoidais em frequências diferentes, para provar que uma onda quadrada pura é na verdade equivalente a uma série de ondas senoidais.

Quando uma tensão CA de onda quadrada é aplicada a um circuito com componentes reativos (capacitores e indutores), esses componentes reagem como se estivessem sendo expostos a várias tensões de onda senoidal de diferentes frequências, o que de fato estão.

O fato de que ondas repetitivas não senoidais são equivalentes a uma série definida de voltagem DC aditiva, ondas senoidais e / ou ondas cossenosas é uma consequência de como as ondas funcionam:uma propriedade fundamental de todos os fenômenos relacionados a ondas, elétricos ou outros.

O processo matemático de redução de uma onda não senoidal nessas frequências constituintes é chamado de análise de Fourier , cujos detalhes estão bem além do escopo deste texto. No entanto, algoritmos de computador foram criados para realizar essa análise em altas velocidades em formas de onda reais, e sua aplicação em qualidade de energia CA e análise de sinal é amplamente difundida.

SPICE tem a capacidade de amostrar uma forma de onda e reduzi-la em seus harmônicos de onda senoidais constituintes por meio de uma Transformada de Fourier algoritmo, gerando a análise de frequência como uma tabela de números. Vamos tentar isso em uma onda quadrada, que já sabemos que é composta de ondas senoidais harmônicas ímpares:

 lista de análise de onda quadrada v1 1 0 pulso (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .tran 1m 40m . traçar tran v (1,0) .quatro 50 v (1,0) .fim 

O pulso opção na linha netlist que descreve a fonte de tensão v1 instrui o SPICE a simular uma forma de onda de "pulso" quadrada, neste caso uma que é simétrica (tempo igual para cada meio-ciclo) e tem uma amplitude de pico de 1 volt. Primeiro, vamos representar graficamente a onda quadrada a ser analisada:

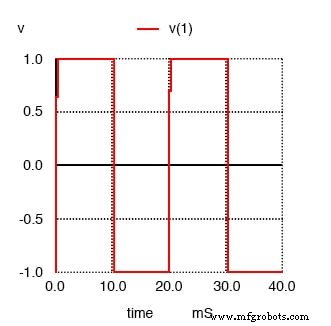
Squarewave para análise SPICE de Fourier



A seguir, imprimiremos a análise de Fourier gerada pelo SPICE para esta onda quadrada:

 componentes de Fourier da resposta transitória v (1) componente dc =-2,439E-02 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 5.000E + 01 1.274E + 00 1.000000 -2.195 0,000 2 1,000E + 02 4,892E-02 0,038415 -94,390 -92,195 3 1.500E + 02 4.253E-01 0.333987 -6.585 -4.390 4 2.000E + 02 4.936E-02 0.038757 -98.780 -96.585 5 2.500E + 02 2.562E-01 0,201179 -10,976 -8,780 6 3.000E + 02 5.010E-02 0.039337 -103.171 -100.976 7 3.500E + 02 1.841E-01 0.144549 -15.366 -13.171 8 4.000E + 02 5.116E-02 0.040175 -107.561 -105.366 9 4.500E + 02 1.443E-01 0.113316 -19.756 -17.561 distorção harmônica total =43,805747 por cento 

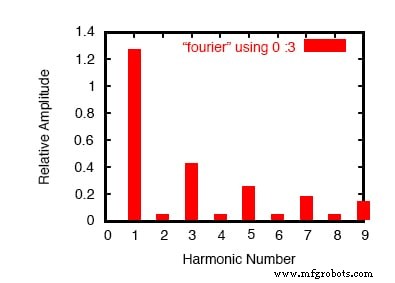
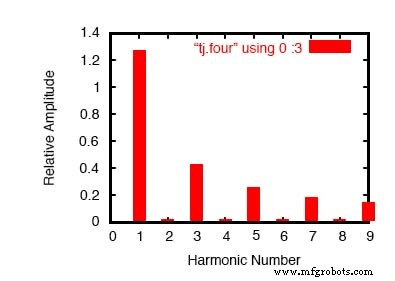
Gráfico dos resultados da análise de Fourier.



Aqui, (Figura acima) SPICE quebrou a forma de onda em um espectro de frequências senoidais até o nono harmônico, mais uma pequena tensão DC rotulada como componente DC .

Tive que informar o SPICE da frequência fundamental (para uma onda quadrada com um período de 20 milissegundos, essa frequência é 50 Hz), para que ele soubesse classificar os harmônicos. Observe como os números são pequenos para todos os harmônicos pares (2o, 4o, 6o, 8o) e como as amplitudes dos harmônicos ímpares diminuem (o 1o é o maior, o 9o é o menor).

Esta mesma técnica de “Transformação de Fourier” é frequentemente usada em instrumentação de potência computadorizada, amostrando a (s) forma (s) de onda CA e determinando o conteúdo harmônico das mesmas. Um algoritmo de computador comum (sequência de etapas do programa para realizar uma tarefa) para isso é a Transformada Rápida de Fourier ou FFT função.

Você não precisa se preocupar exatamente como essas rotinas de computador funcionam, mas estar ciente de sua existência e aplicação.

Essa mesma técnica matemática usada no SPICE para analisar o conteúdo harmônico das ondas pode ser aplicada à análise técnica da música:dividir qualquer som particular em suas frequências de onda senoidal constituintes.

Na verdade, você já deve ter visto um dispositivo projetado para fazer exatamente isso, sem saber o que era! Um equalizador gráfico é um equipamento estéreo de alta fidelidade que controla (e às vezes exibe) a natureza do conteúdo harmônico da música.

Equipado com vários botões ou alavancas deslizantes, o equalizador é capaz de atenuar seletivamente (reduzir) a amplitude de certas frequências presentes na música, para "personalizar" o som para o benefício do ouvinte. Normalmente, haverá um “gráfico de barras” exibido ao lado de cada alavanca de controle, exibindo a amplitude de cada frequência específica.

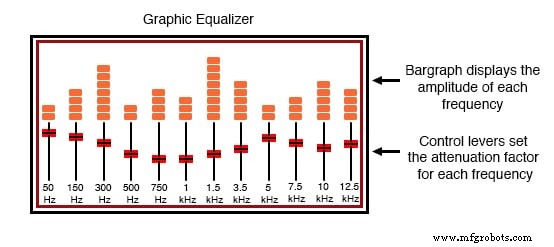
Equalizador gráfico de áudio Hi-Fi.



Um dispositivo construído estritamente para exibir - não controlar - as amplitudes de cada faixa de frequência para um sinal de frequência mista é normalmente chamado de analisador de espectro .

O projeto de analisadores de espectro pode ser tão simples quanto um conjunto de circuitos de "filtro" (consulte o próximo capítulo para detalhes) projetado para separar as diferentes frequências umas das outras, ou tão complexo quanto um computador digital de propósito especial executando um algoritmo FFT para dividir matematicamente o sinal em seus componentes harmônicos.

Os analisadores de espectro são freqüentemente projetados para analisar sinais de frequência extremamente alta, como aqueles produzidos por transmissores de rádio e hardware de rede de computador. Nessa forma, costumam ter a aparência de um osciloscópio:

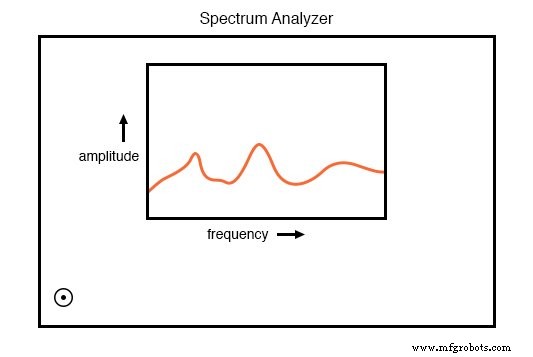
O analisador de espectro mostra a amplitude como uma função da frequência.



Como um osciloscópio, o analisador de espectro usa um CRT (ou um monitor de computador que imita um CRT) para exibir um gráfico do sinal.

Ao contrário de um osciloscópio, este gráfico é a amplitude da frequência em vez de amplitude ao longo do tempo . Em essência, um analisador de frequência dá ao operador um gráfico de Bode do sinal:algo que um engenheiro pode chamar de domínio de frequência em vez de um domínio do tempo análise.

O termo “domínio” é matemático:uma palavra sofisticada para descrever o eixo horizontal de um gráfico. Assim, o gráfico de amplitude (vertical) de um osciloscópio ao longo do tempo (horizontal) é uma análise de "domínio de tempo", enquanto o gráfico de amplitude (vertical) sobre frequência (horizontal) de um analisador de espectro é uma análise de "domínio de frequência".

Quando usamos o SPICE para representar graficamente a amplitude do sinal (seja de tensão ou de corrente) em uma faixa de frequências, estamos realizando o domínio da frequência análise.

Observe como a análise de Fourier da última simulação do SPICE não é "perfeita". Idealmente, as amplitudes de todos os harmônicos pares devem ser absolutamente zero, e o mesmo deve acontecer com o componente CC. Novamente, isso não é tanto uma peculiaridade do SPICE, mas uma propriedade das formas de onda em geral.

Uma forma de onda de duração infinita (número infinito de ciclos) pode ser analisada com precisão absoluta, mas quanto menos ciclos disponíveis para o computador para análise, menos precisa a análise. É apenas quando temos uma equação que descreve uma forma de onda em sua totalidade que a análise de Fourier pode reduzi-la a uma série definida de formas de onda senoidais.

Quanto menos vezes o ciclo de uma onda, menos certa será sua frequência. Levando este conceito ao seu extremo lógico, um pulso curto - uma forma de onda que nem mesmo completa um ciclo - na verdade não tem frequência , mas sim atua como uma gama infinita de frequências. Este princípio é comum a todos fenômenos baseados em ondas, não apenas tensões e correntes AC.

Basta dizer que o número de ciclos e a certeza do (s) componente (s) de frequência de uma forma de onda estão diretamente relacionados.

Poderíamos melhorar a precisão de nossa análise aqui, deixando a onda oscilar continuamente por muitos ciclos, e o resultado seria uma análise de espectro mais consistente com o ideal. Na análise a seguir, omiti o gráfico da forma de onda por uma questão de brevidade - é apenas uma onda quadrada muito longa:

 onda quadrada v1 1 0 pulso (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .option limpts =1001 .tran 1m 1 . traçar tran v (1,0) .quatro 50 v (1,0) .fim componentes de Fourier da resposta transitória v (1) componente dc =9.999E-03 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 5.000E + 01 1.273E + 00 1.000000 -1.800 0,000 2 1.000E + 02 1.999E-02 0.015704 86.382 88.182 3 1.500E + 02 4.238E-01 0.332897 -5.400 -3.600 4 2.000E + 02 1.997E-02 0.015688 82.764 84.564 5 2.500E + 02 2.536E-01 0,199215 -9.000 -7.200 6 3.000E + 02 1.994E-02 0.015663 79.146 80.946 7 3,500E + 02 1,804E-01 0,141737 -12,600 -10,800 8 4.000E + 02 1.989E-02 0.015627 75.529 77.329 9 4.500E + 02 1.396E-01 0.109662 -16.199 -14.399 

Análise de Fourier aprimorada.



Observe como esta análise (Figura acima) mostra menos de uma tensão de componente CC e amplitudes mais baixas para cada uma das ondas senoidais de frequência harmônica pares, tudo porque deixamos o computador amostrar mais ciclos da onda. Mais uma vez, a imprecisão da primeira análise não é tanto uma falha no SPICE, mas uma propriedade fundamental das ondas e da análise do sinal.



REVER:

• Ondas quadradas são equivalentes a uma onda senoidal na mesma frequência (fundamental) adicionada a uma série infinita de harmônicos de ondas senoidais múltiplas ímpares em amplitudes decrescentes.
• Existem algoritmos de computador que são capazes de amostrar formas de onda e determinar seus componentes sinusoidais constituintes. A Transformada de Fourier algoritmo (particularmente a Transformada Rápida de Fourier ou FFT ) é comumente usado em programas de simulação de circuitos de computador, como o SPICE, e em equipamentos de medição eletrônica para determinar a qualidade da energia.

PLANILHAS RELACIONADAS:

• Planilha de sinais de onda quadrada