Outras formas de onda

Por mais estranho que possa parecer, qualquer a forma de onda repetitiva e não senoidal é, na verdade, equivalente a uma série de formas de onda senoidais de diferentes amplitudes e frequências somadas. Ondas quadradas são um caso muito comum e bem conhecido, mas não o único.

Dispositivos de controle eletrônico de potência, como transistores e retificadores controlados de silício ( SCRs ) frequentemente produzem formas de onda de tensão e corrente que são essencialmente versões fragmentadas da onda senoidal AC “limpa” (pura) da fonte de alimentação.

Esses dispositivos têm a capacidade de mudar repentinamente sua resistência com a aplicação de uma tensão ou corrente de sinal de controle, “ligando” ou “desligando” quase instantaneamente, produzindo formas de onda de corrente que apresentam pouca semelhança com a forma de onda de tensão da fonte que alimenta o circuito.

Essas formas de onda de corrente, então, produzem mudanças na forma de onda de voltagem para outros componentes do circuito, devido às quedas de voltagem criadas pela corrente não senoidal através das impedâncias do circuito.

Componentes não lineares

Os componentes do circuito que distorcem a forma de onda senoidal normal da tensão ou corrente CA são chamados de não lineares . Os componentes não lineares, como os SCRs, têm uso popular na eletrônica de potência devido à sua capacidade de regular grandes quantidades de energia elétrica sem dissipar muito calor.

Embora isso seja uma vantagem do ponto de vista da eficiência energética, as distorções da forma de onda que eles introduzem podem causar problemas.

Essas formas de onda não senoidais, independentemente de sua forma real, são equivalentes a uma série de formas de onda senoidais de frequências mais altas (harmônicas).

Se não forem levadas em consideração pelo projetista do circuito, essas formas de onda harmônicas criadas por componentes de comutação eletrônicos podem causar um comportamento errático do circuito.

Está se tornando cada vez mais comum na indústria de energia elétrica observar o superaquecimento de transformadores e motores devido a distorções na forma de onda senoidal da tensão da linha de alimentação CA decorrente de cargas de “comutação”, como computadores e lâmpadas de alta eficiência.

Este não é um exercício teórico:é muito real e potencialmente muito problemático.

Nesta seção, investigarei algumas das formas de onda mais comuns e mostrarei seus componentes harmônicos por meio da análise de Fourier usando SPICE.

Uma forma muito comum pela qual os harmônicos são gerados em um sistema de energia CA é quando a CA é convertida ou “retificada” em CC. Isso geralmente é feito com componentes chamados diodos , que só permitem a passagem da corrente em uma direção.

Retificação de meia onda

O tipo mais simples de retificação AC / DC é meia onda , onde um único diodo bloqueia metade da corrente CA (ao longo do tempo) de passar pela carga. (Figura abaixo)

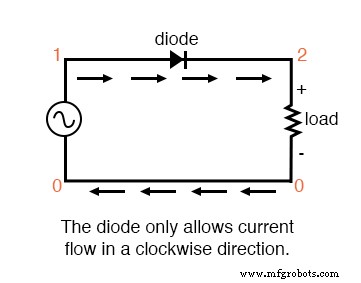
Retificador de meia onda

 retificador de meia onda v1 1 0 sin (0 15 60 0 0) rload 2 0 10k d1 1 2 mod1 .model mod1 d .tran .5m 17m . traçar tran v (1,0) v (2,0) .quatro 60 v (1,0) v (2,0) .fim 

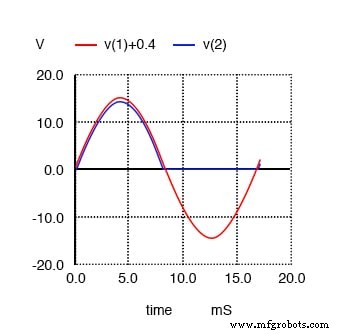
Formas de onda do retificador de meia onda. V (1) +0,4 muda a entrada da onda senoidal V (1) para maior clareza. Isso não faz parte da simulação.



Primeiro, veremos como o SPICE analisa a forma de onda da fonte, uma tensão de onda senoidal pura:(Figura abaixo)

 componentes de Fourier da resposta transitória v (1) componente dc =8.016E-04 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6,000E + 01 1,482E + 01 1,000000 -0,005 0,000 2 1.200E + 02 2.492E-03 0.000168 -104.347 -104.342 3 1.800E + 02 6.465E-04 0.000044 -86.663 -86.658 4 2,400E + 02 1,132E-03 0,000076 -61,324 -61,319 5 3.000E + 02 1.185E-03 0,000080 -70.091 -70.086 6 3,600E + 02 1,092E-03 0,000074 -63,607 -63,602 7 4,200E + 02 1,220E-03 0,000082 -56,288 -56,283 8 4,800E + 02 1,354E-03 0,000091 -54,669 -54,664 9 5,400E + 02 1,467E-03 0,000099 -52,660 -52,655 

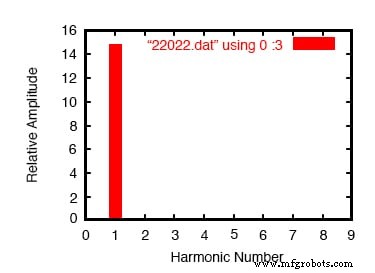
Análise de Fourier da entrada da onda senoidal



Observe os componentes CC e harmônicos extremamente pequenos dessa forma de onda senoidal na tabela acima, embora sejam pequenos demais para serem exibidos no gráfico de harmônicos acima.

Idealmente, não haveria nada além da exibição da frequência fundamental (sendo uma onda senoidal perfeita), mas nossos números de análise de Fourier não são perfeitos porque o SPICE não tem o luxo de amostrar uma forma de onda de duração infinita. A seguir, vamos comparar isso com a análise de Fourier da tensão "retificada" de meia onda através do resistor de carga:(Figura abaixo)

 componentes de Fourier da resposta transitória v (2) componente dc =4,456E + 00 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6,000E + 01 7,000E + 00 1,000000 -0,195 0,000 2 1.200E + 02 3.016E + 00 0.430849 -89.765 -89.570 3 1.800E + 02 1.206E-01 0.017223 -168.005 -167.810 4 2,400E + 02 5,149E-01 0,073556 -87,295 -87,100 5 3.000E + 02 6.382E-02 0.009117 -152.790 -152.595 6 3,600E + 02 1,727E-01 0,024676 -79,362 -79,167 7 4,200E + 02 4,492E-02 0,006417 -132,420 -132,224 8 4,800E + 02 7,493E-02 0,010703 -61,479 -61,284 9 5,400E + 02 4,051E-02 0,005787 -115,085 -114,889 

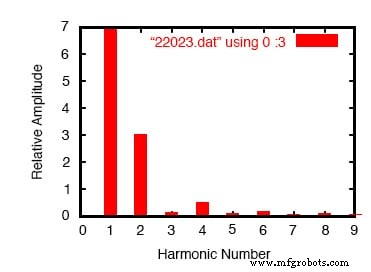
Saída de meia onda da análise de Fourier



Observe os harmônicos pares múltiplos relativamente grandes nesta análise. Cortando metade de nossa onda AC, introduzimos o equivalente a várias formas de onda senoidais de alta frequência (na verdade, cosseno) em nosso circuito a partir da onda senoidal pura original.

Observe também o grande componente DC:4,456 volts. Como nossa forma de onda de tensão CA foi “retificada” (permitida apenas em uma direção através da carga, em vez de para frente e para trás), ela se comporta muito mais como CC.

Retificação de onda completa

Outro método de conversão AC / DC é chamado de onda completa (Figura abaixo), que, como você deve ter adivinhado, utiliza o ciclo completo de energia CA da fonte, invertendo a polaridade da metade do ciclo CA para que os elétrons fluam através da carga na mesma direção o tempo todo.

Não vou aborrecê-lo com detalhes de como exatamente isso é feito, mas podemos examinar a forma de onda (Figura abaixo) e sua análise harmônica por meio do SPICE:

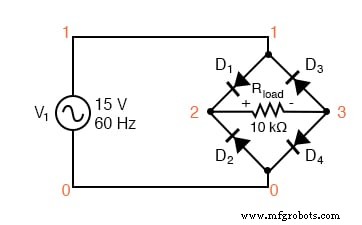
Circuito retificador de onda completa

 retificador de ponte de onda completa v1 1 0 sin (0 15 60 0 0) rload 2 3 10k d1 1 2 mod1 d2 0 2 mod1 d3 3 1 mod1 d4 3 0 mod1 .model mod1 d .tran .5m 17m . traçar tran v (1,0) v (2,3) .quatro 60 v (2,3) .fim 

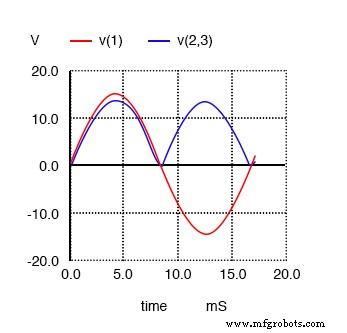
Formas de onda para retificador de onda completa

 Fourier componentes da resposta transitória v (2,3) componente dc =8,273E + 00 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6.000E + 01 7.000E-02 1.000000 -93.519 0,000 2 1.200E + 02 5.997E + 00 85.669415 -90.230 3.289 3 1.800E + 02 7.241E-02 1.034465 -93.787 -0.267 4 2,400E + 02 1,013E + 00 14,465161 -92,492 1,027 5 3.000E + 02 7.364E-02 1.052023 -95.026 -1.507 6 3,600E + 02 3,337E-01 4,767350 -100,271 -6,752 7 4.200E + 02 7.496E-02 1.070827 -94.023 -0.504 8 4.800E + 02 1.404E-01 2.006043 -118.839 -25.319 9 5.400E + 02 7.457E-02 1.065240 -90.907 2.612 

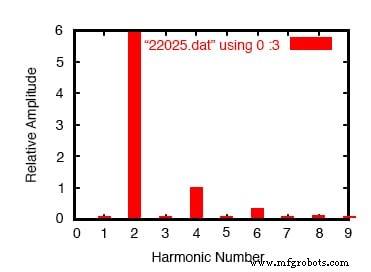
Análise de Fourier da saída do retificador de onda completa



Que diferença! De acordo com a transformada de Fourier do SPICE, temos um segundo componente harmônico para esta forma de onda que é mais de 85 vezes a amplitude da frequência da fonte CA original!

O componente DC desta onda aparece como sendo 8,273 volts (quase o dobro do que era para o circuito retificador de meia onda) enquanto o segundo harmônico tem quase 6 volts de amplitude. Observe todos os outros harmônicos mais adiante na tabela.

Os harmônicos ímpares são, na verdade, mais fortes em algumas das frequências mais altas do que nas mais baixas, o que é interessante.

Como você pode ver, o que pode começar como uma onda senoidal CA simples e limpa, pode terminar como uma confusão complexa de harmônicos depois de passar por apenas alguns componentes eletrônicos.

Embora a matemática complexa por trás de toda essa transformação de Fourier não seja necessária para o estudante iniciante em circuitos elétricos entender, é de extrema importância compreender os princípios em ação e compreender os efeitos práticos que os sinais harmônicos podem ter nos circuitos.

Os efeitos práticos das frequências harmônicas em circuitos serão explorados na última seção deste capítulo, mas antes de fazermos isso, daremos uma olhada mais de perto nas formas de onda e seus respectivos harmônicos.



REVER:

• Qualquer forma de onda, desde que seja repetitiva, pode ser reduzida a uma série de formas de onda sinusoidais somadas. Diferentes formas de onda consistem em diferentes combinações de harmônicos de onda senoidal.
• A retificação de CA para CC é uma fonte muito comum de harmônicos em sistemas de energia industrial.