Reavaliação das distribuições vitalícias de luminescência em nanocristais de silício

Resumo

A dinâmica da luminescência em conjuntos de nanocristais é complicada por uma variedade de processos, incluindo a dependência do tamanho das taxas radiativas e não radiativas em amostras alargadas não homogêneas e interações interpartículas. Isso resulta em um decaimento não exponencial, que para o caso específico dos nanocristais de silício (SiNCs) foi amplamente modelado com uma função Kohlrausch ou "exponencial esticado" (SE). Primeiramente derivamos a função de decaimento da população para um decaimento de luminescência após exp [- ( t / τ) ^β ] Em seguida, comparamos as distribuições e os tempos médios calculados assumindo que o declínio da luminescência ou o declínio da população segue esta função e mostramos que os resultados são significativamente diferentes para β muito abaixo de 1. Em seguida, aplicamos esses dois tipos de funções SE, bem como outros modelos, aos dados de decaimento de luminescência de duas amostras de SiNC cultivadas termicamente com tamanhos médios diferentes. Os tempos de vida médios são fortemente dependentes da configuração experimental e do modelo de ajuste escolhido, nenhum dos quais parece descrever adequadamente a dinâmica de decaimento do conjunto. As técnicas de espectroscopia resolvida em frequência (FRS) são então aplicadas a SiNCs a fim de extrair a distribuição do tempo de vida diretamente. A distribuição da taxa tem meia largura de ~ 0,5 décadas e principalmente se assemelha a uma função lognormal enviesada de alguma alta frequência. A combinação dos métodos TRS e FRS parece mais adequada para descobrir a dinâmica de luminescência de materiais NC com um amplo espectro de emissão.

Introdução

Nanopartículas coloidais podem ser usadas em uma variedade de aplicações, incluindo catálise, tratamentos médicos e aplicações optoeletrônicas [1,2,3,4]. Nanopartículas semicondutoras são de interesse particular para aplicações de emissão de luz, fotovoltaica e fotocatalítica [5, 6]. Nanocristais de silício (SiNCs) são um foco de atenção atual devido às propriedades de emissão ajustáveis ​​[7], bem como à abundância e biocompatibilidade do silício [8]. Para desenvolver tecnologias baseadas em nanopartículas, é necessário um conhecimento profundo das propriedades optoeletrônicas relevantes, e a espectroscopia resolvida no tempo é frequentemente uma ferramenta valiosa para esse propósito.

Os tempos de vida de luminescência de SiNCs são geralmente modelados com uma função exponencial esticada (SE) tendo a forma básica exp [- ( λt ) ^β ], onde o parâmetro de dispersão β assume valores entre 0 e 1, λ é um parâmetro de taxa e t é hora. Esta função é frequentemente descrita como “mais lenta do que exponencial” e implica uma distribuição assimétrica das taxas de decaimento em direção a tempos de vida mais longos. Assim que o β e λ parâmetros foram encontrados pelo ajuste de uma curva de decaimento de luminescência, a distribuição da taxa de decaimento correspondente pode ser aproximadamente reconstruída [9].

A origem da decadência da luminescência SE no silício e em outros pontos quânticos semicondutores tem sido fortemente debatida nas últimas duas décadas, e o debate continuou recentemente [10]. Várias explicações foram propostas para o aparecimento do SE na dinâmica de decaimento, incluindo tunelamento de portadora e aprisionamento em conjuntos de nanocristais estreitamente espaçados [11], a distribuição de tamanho ampliada de forma não homogênea [12], acoplamento elétron-fônon dependente do tamanho [10] , e uma distribuição de alturas de barreira para recombinação não radiativa [13], sendo esta última semelhante a uma sugestão anterior para silício poroso [14]. Claramente, o conhecimento da distribuição de taxa é necessário para uma compreensão do mecanismo de luminescência em SiNCs, bem como em nanocristais semicondutores de forma mais geral.

Em grande parte da literatura anterior sobre SiNCs, o decaimento exponencial estendido foi assumido a priori, geralmente sem análise de outras distribuições possíveis. O SE tende a se ajustar bem visualmente (ou seja, a linha de melhor ajuste parece corresponder bem aos dados "a olho"). Além disso, na grande maioria dos trabalhos anteriores, por exemplo, [15], há uma falta de clareza sobre se a decadência da população ou a decadência da luminescência está realmente sendo modelada. Estes estão relacionados por uma derivada e deve-se usar a expressão correta para entender as escalas de tempo de decaimento na amostra [16]. Além disso, a função de responsividade do detector pode ter um efeito significativo na curva de decaimento de luminescência medida em SiNCs, devido ao amplo espectro de emissão do conjunto. Apesar disso, a responsividade raramente ou nunca foi levada em consideração, dificultando a comparação dos resultados de diferentes investigações. Finalmente, nenhum estudo anterior tentou usar espectroscopia resolvida em frequência (FRS) na análise de nanocristais de silício. Em princípio, o FRS permite que a distribuição do tempo de vida seja extraída sem assumir um modelo a priori.

O objetivo deste artigo é estabelecer uma abordagem para medir, modelar e interpretar a dinâmica de luminescência de nanocristais de silício. Espera-se que isso possa ajudar a compreender melhor a vasta diversidade de resultados muitas vezes contraditórios na literatura, levar a um melhor acordo, ou pelo menos mais consistência, entre as diferentes medições, e a compreender melhor os mecanismos de luminescência.

Teoria Básica

Comparamos três modelos:o exponencial estendido, que é amplamente usado para nanocristais de Si, a distribuição de decaimento lognormal, que foi aplicada pela primeira vez a SiNCs recentemente [17], e o decaimento bimolecular. Para qualquer modelo, a função de densidade de probabilidade de emissão, representada pela integral da função de intensidade g ( t ), no momento t ′ está relacionado à fração de excitações restantes em t ′ de acordo com [16].
$$ {\ int} _0 ^ tg \ left ({t} ^ {\ hbox {'}} \ right) dt =1- \ frac {c_t} {c_0}, $$ (1)
onde c _t e c ₀ é o número de NCs excitados no tempo t e inicialmente. A função de densidade de probabilidade descreve a fração de fótons emitidos entre o tempo 0 e t em relação ao número total de fótons emitidos. Se a redução da população segue uma equação de taxa de primeira ordem (ou seja, recombinação "monomolecular"), temos dc _t / dt = - λc _t , onde λ =1 / τ ₀ , levando ao usual c _t / c ₀ =Exp [- λt ] e g ( t ) = λ⋅ exp [- λt ] depois de obter a derivada de tempo de ambos os lados da Eq. 1. A derivada é necessária porque a intensidade da luminescência medida na janela dt ′ é proporcional à mudança na fração excitada nesse intervalo.

Se considerarmos as taxas radiativa e não radiativa, então substituímos a taxa de decaimento total λ com λ _R + λ _NR para que g ( t ) =( λ _R + λ _NR ) exp [- ( λ _{R +} λ _NR t ] = λ _R exp [- ( λ _{Ri +} λ _NR ) t ] + λ _NR exp [- ( λ _{R +} λ _NR ) t ] em que apenas o primeiro termo é mensurável, produzindo uma intensidade medida para espectroscopia resolvida no tempo (TRS) dada por
$$ g (t) ={\ lambda} _R \ exp \ left [- \ left ({\ lambda} _R + {\ lambda} _ {NR} \ right) t \ right]. $$ (2)
A função de decaimento usada para ajustar os dados, I _t = A · exp (- λt ) + Dc, escalas com um prefator arbitrário adicional, A , que depende da eficiência de detecção e do número de nanopartículas excitadas e levará à escala adequada. Um deslocamento CC é geralmente adicionado à função de decaimento como outro parâmetro de ajuste.

No caso do decaimento exponencial alongado, a fração de emissores excitados decai de acordo com
$$ \ frac {c_t} {c_0} =\ exp \ left [- {\ left ({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right]. $$ (3)
onde λ _SE é a taxa de decaimento exponencial alongada (igual a 1 / τ _SE ) . Inserindo isso na Eq. 1 e tomando a derivada de ambos os lados, como antes, produz uma função de probabilidade de emissão dada por
$$ g (t) ={\ beta \ lambda} _ {SE} ^ {\ beta} {t} ^ {\ beta -1} \ exp \ left [- {\ left ({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right]. $$ (4)
Uma forma de estimar a distribuição de frequências H ( λ ) que leva à Eq. 3 foi mostrado usando uma transformada de Laplace inversa [9], produzindo uma distribuição que se amplia com a diminuição de β e é inclinado para frequências altas.

Infelizmente, na Eq. 4, não é possível separar o prefator em partes radiativas e não radiativas. Isso significa que a Eq. 4 está corretamente normalizado apenas para λ _NR = 0 [16], e a distribuição do tempo de vida obtida a partir de uma curva de decaimento PL só é entendida desta forma. Além disso, há um termo dependente do tempo no prefator; portanto, o declínio da população tem uma dependência do tempo diferente em comparação com o declínio da luminescência [16, 18]. Para obter valores de τ _SE e β para a decadência da população da qual os tempos de vida médios apropriados podem ser extraídos, deve-se usar a Eq. 4 para modelar a decadência observada, onde substituímos g ( t ) pela função de decaimento medida I _t :
$$ {I} _t =A {\ beta \ lambda} _ {SE} ^ {\ beta} {t} ^ {\ beta -1} \ exp \ left [- {\ left ({\ lambda} _ {SE } t \ right)} ^ {\ beta} \ right] + \ mathrm {dc}. $$ (5)
Na Eq. 5, um parâmetro de escala (que também pode absorver o β e λ termos no prefator) e um deslocamento dc foram inseridos como parâmetros de ajuste. A vida média é dada por
$$ \ left \ langle {\ tau} _ {SE} \ right \ rangle =\ frac {\ tau_ {SE}} {\ beta} \ Gamma \ left [\ frac {1} {\ beta} \ right], $$ (6)
onde Γ representa a função Gamma, e o tempo médio de decaimento é
$$ \ left \ langle t \ right \ rangle ={\ tau} _ {SE} \ frac {\ Gamma \ left (2 / \ beta \ right)} {\ Gamma \ left (1 / \ beta \ right)} . $$ (7)
Em muitos trabalhos anteriores, era comum usar o exp exponencial estendido "padrão" [- ( λ _SE t ) ^β ] para modelar a decadência da luminescência em vez da decadência da população. Assim, temos uma função de intensidade normalizada dada por
$$ g (t) =\ frac {\ lambda_ {SE} \ beta} {\ Gamma \ left (1 / \ beta \ right)} \ exp \ left [- {\ left ({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right]. $$ (8)
A Equação 8 é normalizada para que a integração entre t =0 e ∞ é igual a 1. O modelo de ajuste correspondente é simplesmente
$$ {I} _t =A \ exp \ left [- {\ left ({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right] + \ mathrm {dc}. $$ (9)
A Equação 9 é amplamente aplicada e frequentemente se ajusta aos dados de luminescência do SiNC muito bem, apesar do fato de que (como a Eq. 4) a Eq. 8 é estritamente normalizado para uma eficiência quântica absoluta (AQY) de 100%. Um ponto frequentemente esquecido é o fato de que não se pode extrair τ _SE (=1 / λ _SE ) e β do decaimento da luminescência modelado pela Eq. 9 e use-os para calcular os tempos médios com as Eqs. 6 e 7. Essencialmente, as Eqs. 4 e 8 são modelos de decaimento de intensidade diferentes e deve-se esperar funções de decaimento de população, tempos médios e distribuições de taxas de decaimento diferentes.

Para encontrar a decadência da população, isso levaria a uma função de intensidade dada pela Eq. 9, aplicamos o mesmo processo que fizemos para obter a Eq. 4 à Eq. 5, mas ao contrário, isto é:
$$ \ frac {c_t} {c_0} =1- \ frac {\ lambda_ {SE} \ beta} {\ Gamma \ left (1 / \ beta \ right)} {\ int} _0 ^ t \ exp \ left [ - {\ left ({\ lambda} _ {SE} t \ right)} ^ {\ beta} \ right] \ cdot \ mathrm {dt}. $$ (10)
Após várias etapas, a solução da Eq. 10 é
$$ \ frac {c_t} {c_0} =\ frac {1} {\ Gamma \ left (1 / \ beta \ right)} \ Gamma \ left [1 / \ beta, {\ left ({\ lambda} _ { SE} t \ right)} ^ {\ beta} \ right]. $$ (11)
A Equação 11 é a redução da população obtida a partir da redução da intensidade dada pela Eq. 8. Encontrar a vida útil média da maneira usual leva a
$$ \ left \ langle {\ tau} _ {SE} \ right \ rangle ={\ tau} _ {SE} \ frac {\ Gamma \ left (2 / \ beta \ right)} {\ Gamma \ left (1 / \ beta \ right)} $$ (12)
e um tempo médio de decadência de
$$ \ left \ langle t \ right \ rangle ={\ tau} _ {SE} \ frac {\ Gamma \ left (3 / B \ right)} {2 \ Gamma \ left (2 / \ beta \ right)} . $$ (13)
Finalmente, a distribuição de frequência é ( 1 / λ ) · H ( λ ), onde, como antes, H ( λ ) é a distribuição calculada na ref. [9] para uma decadência populacional dada pela Eq. 3. Esses resultados estão resumidos na Tabela 1.

As diferenças entre as duas fórmulas SE são significativas (Fig. 1). Na literatura, freqüentemente se descobre que a diminuição da intensidade é modelada por A · exp [- ( t / τ _SE ) ^β ] + Dc (ou seja, Eq. 9) e, em seguida, os tempos médios são calculados usando Eqs. 6 e 7. Isso parece ser matematicamente incorreto, uma vez que as Eqs. 6 e 7 são derivados de uma queda de intensidade dada pela Eq. 4, não Eq. 8. Por exemplo, tomando τ _SE =100 μs e β =0,7, como mostrado na Fig. 1, para uma queda de intensidade dada por exp [- ( t / τ _SE ) ^β ], encontramos uma constante de tempo média de 199 μs (Eq. 12), em comparação com 127 μs usando a Eq. 6. Diferenças semelhantes são encontradas para os tempos médios de decaimento (Eqs. 7 e 13). Além disso, existe uma abordagem conhecida como método de Higashi-Kastner para estimar uma vida útil característica [19], que tem sido aplicada a SiNCs como uma alternativa à aplicação do modelo de decaimento SE [20, 21]. Neste modelo, o tempo de atraso característico, t _d , é simplesmente considerado como o pico dos dados de decaimento plotados como I _t · t vs. t . Foi sugerido que isso fosse equivalente a ( 1 / β ) ^{1 / β} · τ _SE obtido da Eq. 9 [20].

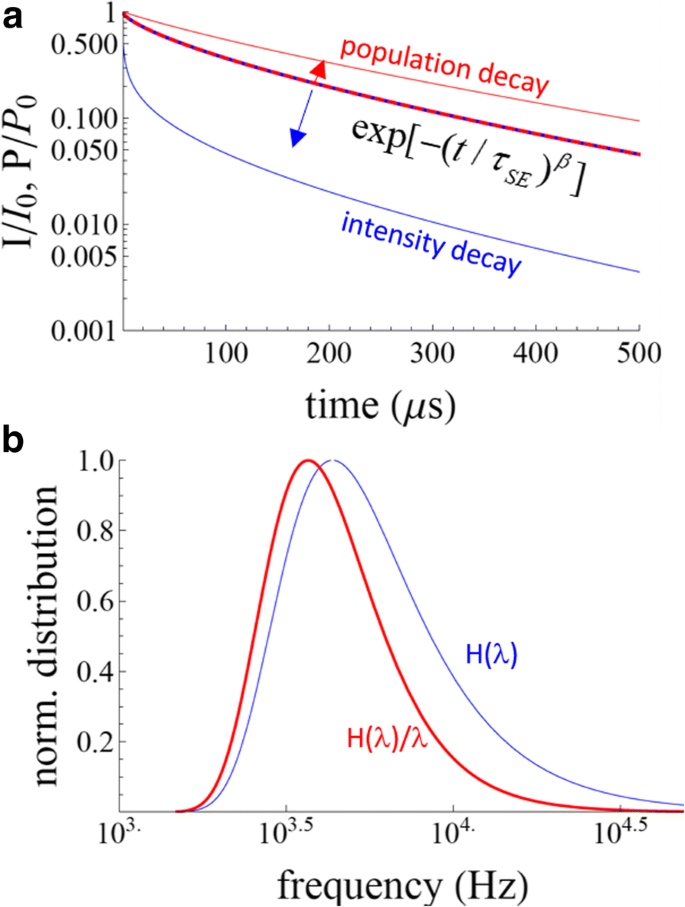
Exponenciais estendidas. a A população e a intensidade decaem para a função exponencial esticada com τ _SE =100 μs e β =0,7. A linha tracejada azul-vermelha é exp [ - ( λt ) ^β ] Se isso representar o declínio da população, então o declínio da intensidade será dado pela linha azul. Se exp [ - ( λt ) ^β ] é o declínio da intensidade, então o declínio da população é mostrado com a linha vermelha. b As distribuições de taxas correspondentes

Alternativamente, a distribuição das taxas de decaimento pode seguir um Η específico ( λ ), levando a uma degradação da luminescência dada por:
$$ g (t) ={\ int} _0 ^ {\ infty} \ mathrm {H} \ left (\ lambda \ right) \ cdot \ exp \ left (- \ lambda t \ right) \ mathrm {d} \ lambda, $$ (14)
onde Η ( λ ) representa a distribuição dependente da frequência das taxas de decaimento. A Equação 14 se reduz à Eq. 2 se Η ( λ ) é igual à função delta de Dirac δ ( λ - λ ₀ ), ou pode representar uma série contínua de exponenciais ponderados pela distribuição selecionada. Uma função lognormal parece uma escolha razoável em sistemas nanocristais, uma vez que muitos conjuntos nanocristais seguem naturalmente distribuições de tamanho lognormal [22]. A fim de evitar mais confusão, usamos a definição normalizada padrão da função lognormal dada por:
$$ H \ left (\ lambda \ right) =\ frac {1} {\ lambda} \ cdot \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp \ left [- \ frac {{\ esquerda (\ ln \ lambda - \ mu \ direita)} ^ 2} {2 {\ sigma} ^ 2} \ direita]. $$ (15)
de modo que a função de decaimento medida é
$$ {I} _t =A \ cdot {\ int} _0 ^ {\ infty} \ left (\ frac {1} {\ lambda} \ cdot \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ exp \ left [- \ frac {{\ left (\ ln \ lambda - \ mu \ right)} ^ 2} {2 {\ sigma} ^ 2} \ right] \ cdot \ exp \ left (- \ lambda t \ direita) d \ lambda \ direita) + dc. $$ (16)
Tal como acontece com a função SE, existem apenas duas variáveis ​​independentes (bem como um deslocamento e um fator de escala). Os momentos são definidos como de costume; ou seja, a taxa média é dada por exp ( μ ), a média por exp ( μ + σ ² / 2), e o tempo de vida mais provável (o pico da distribuição) é exp ( μ - σ ² ) Anteriormente, uma distribuição não padrão foi empregada [16] (ou seja, uma distribuição que, embora válida por conta própria, não é a função de distribuição log-normal comumente aceita). A Equação 14 também se aplica a uma distribuição de decaimento radiativo (isto é, AQY =100%). Na verdade, foi sugerido que as distribuições da taxa de decaimento são ponderadas por uma função de eficiência quântica (desconhecida) [16]. Em situações reais, basta aceitar esta advertência, visto que é difícil ou impossível saber a distribuição populacional das taxas não radiativas na amostra.

Decaimentos de luminescência também podem corresponder a uma reação de segunda ordem (isto é, o decaimento "bimolecular") [23]. Aqui, a taxa na qual a população decai é dada por dc / dt =- λ [ c _t ] ² , que produz uma fração restante c _t / c ₀ =( c ₀ λt + 1) ⁻¹ . Inserindo esta expressão na Eq. 1 resulta em uma decadência da lei de potência:
$$ {I} _t / {I} _0 =A \ frac {\ lambda {c} _0} {{\ left (\ lambda {c} _0 + 1 \ right)} ^ 2}. $$ (17)
O modelo bimolecular tem apenas uma constante de taxa λ (ao contrário do exponencial alongado e do lognormal, que têm distribuições de taxas), e não há vida média. Mais especificamente, a integral de tempo diverge e o tempo de vida médio do decaimento de segunda ordem é infinito.

A função SE “padrão” (Eq. 9) tem sido de longe o modelo dominante usado para decaimentos de luminescência do SiNC, com muitos artigos dedicados a interpretar o significado do decaimento para os mecanismos de luminescência. A distribuição lognormal de tempo de vida foi aplicada pela primeira vez a SiNCs recentemente [17, 24, 25]. Obviamente, há pouca razão a priori para assumir qualquer modelo e, em vez disso, seria preferível estabelecer a distribuição das taxas de decaimento diretamente. Isso pode, pelo menos em princípio, ser alcançado por espectroscopia resolvida em quadratura de frequência (QFRS), que foi aplicada em várias ocasiões ao silício amorfo, mas não aos SiNCs.

Espectroscopia resolvida com frequência de quadratura

O método QFRS é pouco relatado na literatura, principalmente limitado a alguns estudos de vidros dopados com terras raras [26,27 e a-SiOx:H . Mater Sci Eng B 105:165-168 "href =" / articles / 10.1186 / s11671-018-2785-x # ref-CR28 "id =" ref-link-section-d291096563e3613 "> 28] e silício amorfo [29, 30,31]. A base da técnica é excitar a amostra com um feixe de bomba modulado por onda senoidal de frequência angular ω e medir a fase e a amplitude da luminescência enquanto tenta rastrear a excitação. Com esta configuração, o componente de quadratura ( Q ) de um detector sensível à fase (ou seja, um amplificador lock-in) fornece uma medida direta da distribuição da vida útil [30]. Uma vez que a amplitude da oscilação do laser modulada por AOM pode ser dependente da frequência, o componente de quadratura do PL, Q _PL = Z _PL pecado ( Δθ _PL ) deve ser normalizado para a amplitude da oscilação do laser, Z _LA .

O sinal FRS de quadratura é complicado pelo fato de que um único decaimento exponencial não resulta em uma função delta no espectro QFRS. O sinal observado é de fato a convolução da distribuição do tempo de vida com uma única função de resposta exponencial dada em uma escala logarítmica por [31].
$$ {S} _ {\ log_ {10} \ mathrm {r}} =\ frac {{\ omega \ tau} _0} {1 + {\ omega} ^ 2 {\ tau} _0 ^ 2}, $$ (18)
Onde a constante de tempo τ ₀ = ω ₀ ⁻¹ . Assim, a menos que a distribuição da taxa de decaimento tenha várias décadas de largura, uma deconvolução deve ser realizada a fim de extrair uma distribuição significativa.

Resultados e discussão

Caracterização básica

Devido ao baixo contraste associado aos SiNCs e ao contraste mosqueado sobreposto do suporte de carbono amorfo, algoritmos de contagem de partículas baseados em computador usando imagens de campo claro não podem ser aplicados e os diâmetros tiveram que ser estimados "a olho" usando software de contagem de pixels ( imagens de TEM de campo claro de amostra são mostradas na Fig. 2a, d e os resultados da contagem manual de partículas foram ajustados com uma distribuição lognormal (Fig. 2c, f) a fim de obter um diâmetro médio linear de 2,9 nm (média e desvio padrão de os logaritmos naturais μ =1,057 e σ =0,1555) e 5,4 nm ( μ =1,663 e σ =0,1917), para temperaturas de recozimento de 1100 e 1200 ° C, respectivamente. Essas amostras serão doravante referidas como SiNCs “pequenos” e “grandes”. Os tamanhos foram posteriormente verificados por imagens de alta resolução de NCs selecionados (Fig. 2b, e), onde as franjas da rede poderiam ser usadas como outra forma de identificar os NCs e estimar seus diâmetros. A espectroscopia de infravermelho com transformada de Fourier (FTIR) e os dados de XPS mostraram que os SiNCs preparados foram funcionalizados com sucesso com dodeceno; entretanto, os SiNCs pequenos são mais oxidados do que os grandes e, portanto, apresentam um menor grau de funcionalização (Arquivo adicional 1:Figuras S1 e S2).

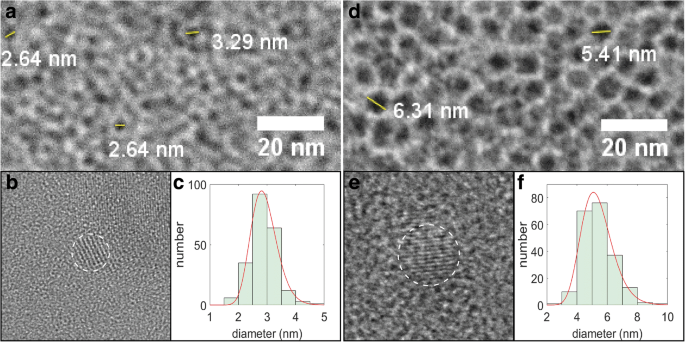
Imagens TEM de SiNCs. a Campo claro, b alta resolução e c histograma de distribuição de tamanho para os pequenos SiNCs. Painéis d - f representam um conjunto semelhante de imagens de grandes SiNCs

Fotoluminescência e espectroscopia resolvida com o tempo

Os espectros de fotoluminescência (PL) foram centralizados em 660 e 825 nm, com largura total na metade máxima de 123 e 198 nm para SiNCs pequenos e grandes, respectivamente (Fig. 3 inserções). As energias indiretas do bandgap são de 1,87 e 1,37 eV de acordo com \ ({E} _g \ kern0.5em =\ kern0.5em \ sqrt {E_ {g, \ mathrm {bulk}} ^ 2 \ kern0.5em + \ kern0.5em D / {R} ^ 2} \) [32] com D =4,8 eV ² / nm ² e R sendo o raio NC, que está de acordo com as partículas pequenas, mas prevê um bandgap ligeiramente menor do que o obtido pelo pico de PL para as grandes. O AQY foi de 12% para a amostra pequena de SiNC e 56% para os grandes NCs. As medições independentes em um sistema diferente renderam 18% e 48% para as duas amostras, o que é típico das incertezas nas medições AQY [33] para os diferentes comprimentos de onda de excitação e corte. Nossa hipótese é que as superfícies menos curvas e de menor energia dos NCs maiores levam a uma melhor funcionalização da superfície e a uma menor contribuição de estados de superfície não radiativos para o espectro PL geral.

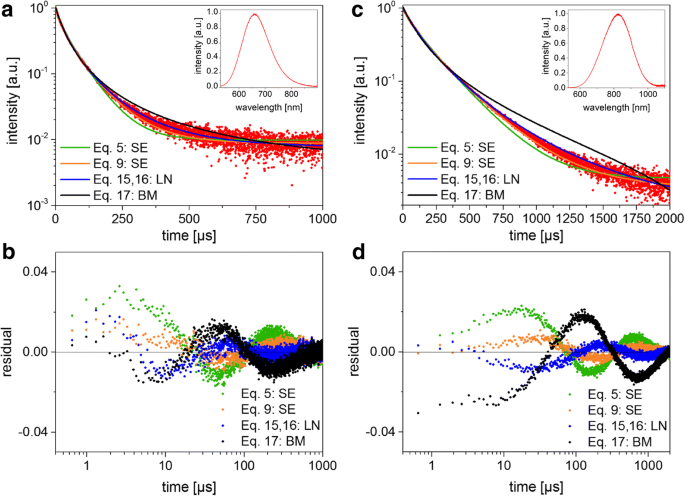
Dados TRS e resultados de ajuste. a Decai a luminescência e a função de ajuste correspondente ( BM bimolecular, SE exponencial estendido, LN lognormal) para pequenos SiNCs. O espectro PL é mostrado na inserção. b Parcelas de resíduos para os ajustes ( a , c , d ) mostram as curvas e os resíduos para os grandes SiNCs.

Ambas as amostras produziram um decaimento não exponencial, como esperado com base na extensa literatura anterior sobre SiNCs. Os decaimentos PL medidos foram ajustados com Eqs. 5, 9, 16 e 17 para testar os diferentes modelos usando minimização de soma de quadrados padrão (Fig. 3). O fato de que a responsividade do detector não é constante ao longo do amplo espectro de luminescência NC será discutido posteriormente. Para todos os casos, os resíduos oscilam, indicando que nenhum dos modelos parece totalmente adequado, mas o modelo SE “simples” (Eq. 9) e o lognormal (Eq. 16) tendem para a menor soma dos quadrados dos resíduos. Os parâmetros de ajuste calculados e tempos de vida médios para as duas amostras de SiNC são mostrados na Tabela 2, em que as médias são claramente dependentes da seleção do modelo de decaimento. O método de Higashi-Kastner também foi aplicado (Fig. 4) e as posições de pico determinadas pelo ajuste das curvas de tempo de retardo com uma Gaussiana enviesada. O método Higashi-Kastner produz uma constante de tempo t _d bastante semelhante a ( 1 / β ) ^{1 / β} ∙ τ _SE , com esses valores retirados da Eq. 9 como mostrado antes [20]. O modelo bimolecular se ajusta muito mal, consistente com nanocristais isolados que não são muito superexcitados. Portanto, não será mais discutido.

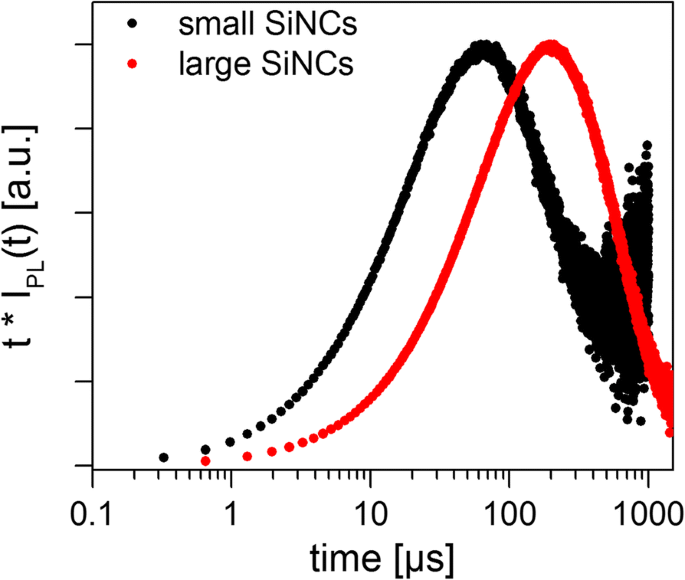
Curvas de decaimento PL normalizadas multiplicadas pelo tempo de decaimento (gráficos de Higashi-Kastner) para os conjuntos de SiNC pequenos e grandes. As posições de pico representam o tempo de decaimento mais dominante, representado por t _d na Tabela 2

A fim de estimar o número de excitons por NC em média para essas condições de medição, a taxa de excitação deve ser calculada a partir das seções transversais de absorção, que podem evidentemente ser tão altas quanto 10 ⁻¹⁴ cm ² para esses experimentos [34]. Dada uma irradiância de excitação de 4500 W / m ² a 352 nm e as taxas de emissão de pico medidas (consulte as seções a seguir), o número de excitações por NC para os SiNCs grandes e pequenos foi estimado em menos de ~ 1 e 0,2, respectivamente. Isso sugere que os grandes SiNCs podem estar um pouco superexcitados. Isso pode causar efeitos não radiativos adicionais devido à presença de multi-excitons em alguns NCs. Para avaliar melhor essa possibilidade, o tempo de vida foi medido em função da potência de excitação; para 2% dos valores relatados acima. Os resultados não mostraram nenhuma tendência e foram sempre os mesmos dentro de ~ 2% (arquivo adicional 1 Figura S3), o que está próximo dos erros de ajuste e repetibilidade, apesar da baixa relação sinal-ruído nas medições de baixa potência. Assim, a possível superexcitação das CNs parece ter pouco efeito nos resultados.

A fim de estimar a distribuição da vida útil do TRS, os decaimentos foram medidos em um conjunto de comprimentos de onda fixos usando um monocromador com passagem de banda de ~ 3 nm (Fig. 5). Devido à baixa intensidade, um sistema PMT de contagem de fótons foi usado para esse propósito. Com radiação efetivamente monocromática, não deve haver diferença nas constantes de decaimento medidas com diferentes detectores, uma vez que há uma distribuição desprezível da função de resposta em uma faixa tão estreita de comprimentos de onda. A mesma tendência foi encontrada para as partículas terminadas em dodecil conforme observado em outras NCs de silício [25, 35, 36]; ou seja, o parâmetro de dispersão aumenta mais próximo da unidade e o tempo de vida aumenta rapidamente em função do comprimento de onda (Fig. 5, Tabela 3).

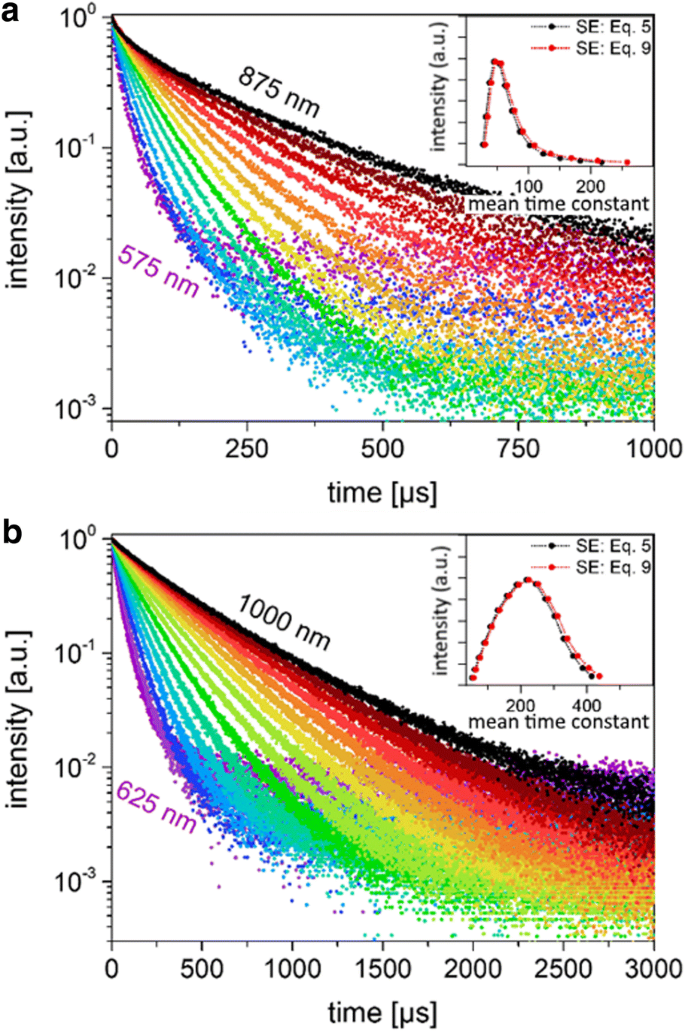
Decai PL de comprimento de onda estreito. a A luminescência decai para os pequenos SiNCs em comprimentos de onda de emissão específicos (3 nm FWHM) variando de 575 a 875 nm, em intervalos de 25 nm. Os dados foram ajustados com as Eqs. 5 e 9, que produziram um ajuste exponencial quase único. b A luminescência decai em comprimentos de onda de emissão específicos que variam de 625 a 1000 nm para os grandes SiNCs medidos e ajustados nas mesmas condições. As constantes de tempo resultantes para o pequeno e o grande SiNCs são fornecidas na Tabela 1

As partículas menores sempre tiveram uma vida útil mais curta do que as maiores no mesmo comprimento de onda de medição. Essa observação é consistente com o AQY mais baixo das partículas menores, indicando que a vida útil das grandes NCs é menos fortemente governada por processos não radiativos. Os grandes NCs também são menos oxidados em comparação com a pequena amostra NC (arquivo adicional 1 Figura S1). Assim, embora a observação do AQY inferior na amostra pequena seja consistente com os tempos de vida mais curtos medidos, não se pode fazer uma comparação relativa das duas amostras por meio da seleção do comprimento de onda (basicamente, o comprimento de onda de emissão depende do tamanho e o grau de oxidação [24], que é diferente nas duas amostras).

Também plotados como inserções na Fig. 5 são as distribuições obtidas plotando os tempos de vida médios obtidos a partir dos dados monocromados, usando Eqs. 5 ou 9 para ajustar os dados, como uma função da intensidade PL nesse comprimento de onda. Uma vez que, para esses decaimentos, o parâmetro beta é razoavelmente próximo de 1, há bastante pouca diferença entre os tempos de vida médios calculados com as duas versões do modelo SE e as distribuições obtidas dessa maneira parecem semelhantes. Embora esses decaimentos não representem a distribuição “verdadeira” de vidas úteis devido às contribuições não radiativas para I _PL , eles podem, no entanto, fornecer uma indicação da distribuição ao longo da vida. Para as partículas pequenas, observamos um pico em ~ 47 μs, enquanto para as grandes NCs o pico é mais simétrico e centrado em torno de 220 μs.

Espectroscopia resolvida por frequência

Começamos validando os dados de FRS de dois padrões de teste:o primeiro era um circuito RC e o segundo era uma amostra de microesferas dopadas com quelato de Eu fluorescente (Fisher Scientific). O circuito RC tem um decaimento monoexponencial no qual os dados do FRS correspondem à Eq. 9 bastante próximo e atingiu o pico em 12,7 kHz, de acordo com a constante de tempo de decaimento medida de 78,9 μs. O espectro de Eu-quelato PL atingiu o pico em 650 nm com um tempo de decaimento da ordem de centenas de microssegundos, apresentando um padrão para os Si NCs. A luminescência também decaiu quase monoexponencialmente com uma vida útil de 670 μs. Os dados do FRS foram centralizados em ~ 1570 Hz com uma largura virtualmente igual à função de resposta (Eq. 18), que é bastante próxima ao resultado do TRS observado. A diferença (636 vs. 670 μs) pode ser devido ao comportamento ligeiramente não exponencial do decaimento acoplado ao método de excitação, conforme discutido mais abaixo.

Os dados FRS para os Si-NCs são problemáticos porque os resultados QFRS observados revelaram-se apenas ligeiramente mais amplos do que a função de resposta (consulte a inserção da Fig. 6a). Portanto, uma deconvolução deve ser realizada nos dados, que precisam estar quase livres de ruído para evitar problemas significativos com o procedimento de deconvolução. Usamos o método de deconvolução de Richardson-Lucy [37] para impor uma restrição de positividade. Os dados QFRS deconvolvidos e normalizados, então, fornecem a distribuição do tempo de vida medido diretamente, como mostrado na Fig. 6 para os NCs grandes e pequenos, respectivamente (pontos vermelhos), sem assumir qualquer modelo a priori. Para ambas as amostras, encontramos uma ampla distribuição de tempo de vida que, no caso dos grandes NCs, é ligeiramente inclinada em direção às frequências mais altas, enquanto a pequena distribuição dos NCs é mais quase simétrica em um gráfico semilog. A distribuição da taxa de decaimento atingiu o pico em 19.900 Hz (50,3 μs) para os NCs pequenos, enquanto que para os NCs maiores a distribuição atingiu o pico em 6280 Hz (159,2 μs).

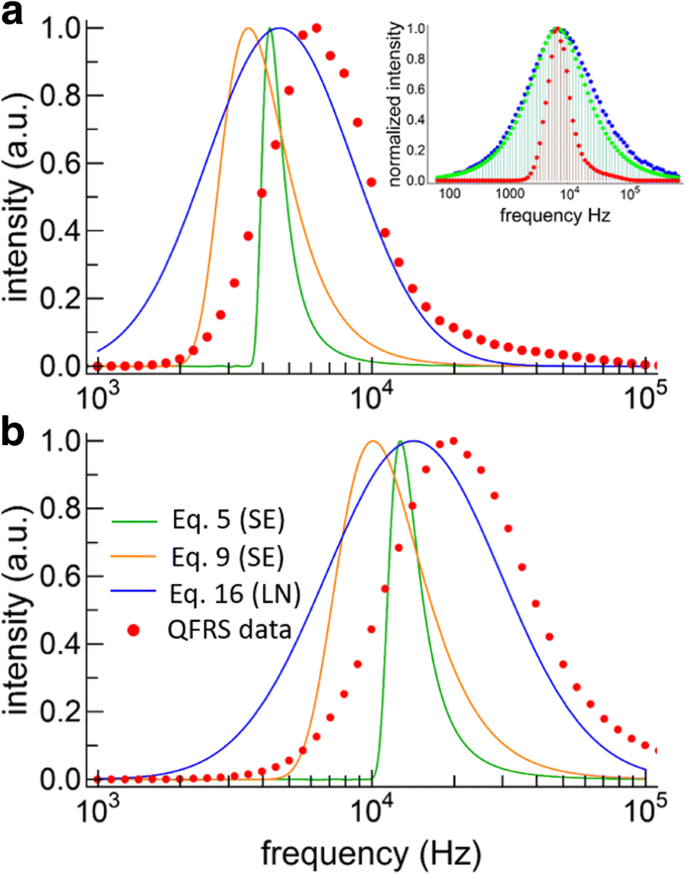
Lifetime distributions. a Lifetime distributions for large SiNCs obtained from fitting the TRS data with the two SE models and the LN model. The deconvolved QFRS data is also shown (red points). The inset shows the raw QFRS data for this sample (blue), the response function (green), and the deconvolution (red). b Lifetime distributions obtained by model fitting the TRS data (lines, same color scheme for both graphs) and QFRS (red points) for the small SiNCs

The lifetime distributions obtained from the stretched exponentials (orange and green curves) and lognormal (blue curve) model fits are also plotted in Fig. 6 for the large and small particles. The three decay models yield different distributions, both in terms of the overall shape and the peak frequencies. For both samples, the QFRS peaks at a higher frequency than any of the TRS model fits. While this may seem surprising, the same effects have been observed for CdSe NCs having a distribution of lifetimes [38, 39]. In fact, the TRS decay curve for CdSe NCs was evidently sensitive to the pulse duration, with shorter pulses accentuating the shorter lifetimes and the opposite case for long pulses. Furthermore, the mean lifetimes obtained by long-pulse duration techniques were a factor of 3–4 times longer than those obtained by phase measurement, which was due to preferential excitation of the long-lived population in steady-state excitation [38]. Indeed, the response function for TRS with a slow repetition rate is narrower than for FRS, cutting off especially sharply on the high frequency side [29]. Essentially, FRS accentuates the short-lived components of the ensemble decay more than steady-state TRS does, and this may account for the difference in the peak frequencies obtained by TRS model fitting and FRS. Despite these inherent differences, FRS appears suited to uncovering the distribution of lifetimes in ensembles of SiNCs, because it is obtained by direct measurement rather than by an assumed model. For SiNCs typical of a thermally grown ensemble, the main drawback of FRS is the necessity of a deconvolution.

While the detector response function certainly affects the QFRS, it plays a role in the TRS data as well. Indeed, measuring the ensemble decay with the APD vs. the PMT setup yielded mean decay times that were different by a factor of ~ 2, regardless of the fitting model applied. The detector responsivity also affects choice of the TRS “best” model fit. As mentioned above, our Thorlabs APD responsivity peaks at 600 nm, whereas for our Hamamatsu PMT the responsivity maximizes at 850 nm, in the long-wavelength, slow-decay part of the SiNC spectrum. Although apparently not reported before in the literature on SiNCs, this issue means that wide-spectrum TRS results from different setups are not comparable. Unfortunately, despite some critical conclusions, ref. [38] also used different detectors to compare the decay dynamics from the same wide-band NC sample and the response functions may not have been the same. Fortunately, however, the phase measurements and the steady-state measurements used the same detector (as was the case here) and the differences in the observed dynamics for these situations remain valid. Finally, the detector response function is in principle correctable in the FRS data if the responsivity curve and monochromated decay rate distribution are known over a wide range of wavelengths (i.e., decay rates). The responsivity correction has no such simple solution with TRS alone.

Conclusões

The most common models used for SiNC luminescence decay were described theoretically. The population decay corresponding to the “simple” stretched exponential luminescence decay, exp[− (t /τ ) ^β ], was derived and expressions for the characteristic mean times were found. This model was compared against the alternative model in which the population decays according to the simple SE. Two dodecene-functionalized SiNCs samples were then prepared from thermal nucleation and growth, followed by etching and alkane surface functionalization. These samples consisted of particles with mean diameters of 2.9 and 5.4 nm, respectively. The basic PL spectrum and TRS was measured using standard methods. The TRS data were fit with several distributions in order to establish whether any of them can be considered “true” and to find which one yields the best fit. While the simple SE luminescence decay fits the TRS data reasonably well, the distribution of residuals shows that it is not strictly accurate. None of the fitting models fully captures the shape of the measured decay rate distribution; they also show large deviations in the peak position and the shape of the distribution, as well as disagreement in the average time constants. Furthermore, the ensemble mean time constants were dependent on the responsivity curve of the detection system. This leads to serious questions about how to interpret the PL decay from ensembles of thermally-grown SiNCs.

Quadrature frequency-resolved spectroscopy was then employed with the intent to find the lifetime distribution directly for SiNC ensembles formed by thermal annealing of a base oxide. The spectrum was found to be not much wider than the intrinsic QFRS response function, requiring a deconvolution in order to extract the SiNC rate distribution. This yielded a distribution whose shape was nearly symmetrical (on a semilog scale) for the small NC sample and about half a decade wide, whereas it was slightly more skewed for the large NCs. We find that FRS techniques are suited to the study of SiNC luminescence dynamics and, after deconvolving the system response from the data, FRS yields the decay rate distribution directly. The most significant problem is the required deconvolution, but the Richardson-Lucy method was found to produce fairly robust results. While the detector response function can in principle be corrected from the FRS data, there is no simple means to do this for wide-PL-band TRS data. Still, as long as the data compared are from the same detector then the results should at least be internally meaningful. Hopefully in the future, these issues will be more fully considered when analyzing inhomogeneously broadened NC luminescence lifetimes, rather than defaulting to the simple stretched exponential model (Eq. 9) to describe and characterize the dynamical processes at work in the PL spectrum.

Methods

The SiNCs were synthesized according to a recently-proposed method [21]. Briefly, 4 g of hydrogen silsesquioxane (HSQ) was annealed at 1100 or 1200 °C for 1 h in a flowing 5% H₂  + 95% Ar atmosphere, resulting in composites of SiNCs embedded in a silica matrix. These composites were mechanically ground into a fine powder using an agate mortar. The powder was shaken for about 8 h with glass beads using a wrist action shaker. The powders were suspended in 95% ethanol and interfaced to a vacuum filtration system equipped with a filter. To liberate the H-SiNCs, the silica matrix was removed via HF etching. An approximately 200 mg aliquot of the composite was transferred to a Teflon beaker to which 2 mL of ethanol, 2 mL of water, and 2 mL of 49% HF aqueous solution were added in order to dissolve the silica matrix. After stirring the suspension for 40 min, the liberated H-SiNCs were extracted as a cloudy yellow suspension using toluene and isolated by centrifugation at 3000 rpm for 5 min. The resulting hydrogen-terminated SiNCs were suspended in 10 mL dry toluene, and then transferred to an oven-dried Schlenk flask equipped with a magnetic stir bar. Subsequently, 1 mL of 1-dodecene (ca. 4.6 mmol), as well as 20 mg of AIBN were added. The suspension was subjected to three freeze-pump-thaw cycles using an Ar charged Schlenk line. After warming the suspension to room temperature, it was stirred for 24 h at 70 °C, and 10 mL of methanol and 20 mL of ethanol were subsequently added to the transparent reaction mixture. The resulting cloudy suspension was transferred to a 50 mL PTFE vial and the SiNCs were isolated by centrifugation at 12,000 rpm for 20 min. The SiNCs were re-dispersed in 10 mL toluene and isolated by addition of 30 mL ethanol antisolvent followed by another centrifugation. The latter procedure was carried out one more time. Finally, the dodecyl-SiNCs were re-dispersed in 5 mL dry toluene and stored in a screw capped vial (concentration ~ 0.5 mg/mL) for optical studies.

TEM samples were prepared by depositing the freestanding nanoparticles directly onto an ultrathin (ca. 3 nm) carbon-coated copper TEM grid. The NCs were imaged by bright-field TEM using a JEOL JEM-2010 and HRTEM was done on a JEOL JEM-ARM200CF. Fourier transform infrared spectroscopy (FTIR) was performed in a Nicolet 8700 from Thermo Scientific. X-ray photo-electron spectroscopy was measured in a SPECS system equipped with a Phoibos 150 2D CCD hemispherical analyzer and a Focus 500 monochromator. The detector angle was set perpendicular to the surface and the X-ray source was the Mg Kα line.

Luminescence spectra were excited with a 352-nm Ar ⁺ ion laser, which was pulsed (50% duty cycle, 50–250 Hz) using an Isomet IMDD-T110 L-1.5 acousto-optic modulator (AOM) with a fall time of ~ 50 ns. The used setup is schematically depicted in Fig. 7. The laser beam passes the acousto-optic modulator and one of the diffracted beams is selected by an iris. A beamsplitter reflects the main part of the pulsed laser beam into the sample cuvette and the incident power on the sample was ~ 8 mW spread over an area of ~ 4 mm ² . The luminescence was collected with an optical fiber (numerical aperture 0.22), sent through a 450-nm longpass filter and is guided to the appropriate detector. The PL spectrum was measured by an Ocean Optics miniature spectrometer whose response function was corrected using a calibrated radiation source (the HL-3 + -CAL from Ocean Optics). The quantum efficiency was measured using an integrating sphere with 405-nm excitation, using a solution diluted to have an absorbance of ~ 0.15 at that wavelength.

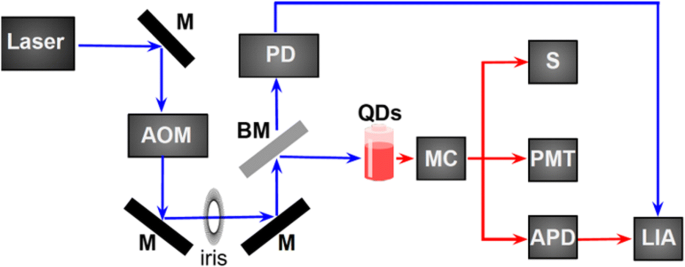
Diagram of the experimental setup. M mirror, AOM acousto-optic modulator, BM beamsplitter, PD photodiode, MC monochromator, S spectrometer, PMT photomultiplier tube, APD avalanche photodiode, LIA lock-in amplifier

The luminescence dynamics were measured with two different detectors. The first detector was the Thorlabs 120A2 avalanche photodiode (50 MHz roll-off), which was interfaced to a Moku:Lab (200 MHz) in digital oscilloscope mode. The second detector was a Hamamatsu h7422-50 photomultiplier tube interfaced to a Becker-Hickl PMS400 multiscalar. The error in the luminescence decay times was obtained by repeating the measurements three times, yielding a standard error in the mean lifetime calculated using the stretched exponential fit (Eq. 4) of 1 μs. All fits to the decay data were done in Origin using the least linear squares with the Levenberg-Marquardt algorithm, and were repeated in Matlab using the same method. For wavelength-dependent decay measurements, the luminescence was sent through an Acton MS2500i monochromator prior to detection, with the half width of the detected radiation set to ~ 3 nm.

For QFRS measurements, the AOM was set to produce a sinusoidal oscillation. A part of the incident beam was deflected into a Thorlabs PDA10A photodiode (200 MHz) in order to generate the reference signal. The SiNC PL response was simultaneously collected and sent to the APD. The reference signal was obtained using the beamsplitter, and along with the corresponding PL signal, was analyzed using the Moku:Lab in the lock-in amplifier mode to measure the in-phase and quadrature components of the signal.

Finally, we also searched for a short-lifetime component in the luminescence, as has sometimes been reported previously and attributed to oxidation [22]. This system used a 405-nm picosecond diode laser (Alphalas GmbH) to excite the NCs, and a Becker-Hickl HPM-100-50 PMT interfaced to an SPC-130 pulse counter system. This setup has a response time of ~ 100 ps. No evidence of a nanosecond decay was observed in these SiNCs.

Abreviações

APD:

Avalanche photodiode

AQY:

Absolute quantum yield

FRS:

Frequency-resolved spectroscopy

LN:

Lognormal

NCs:

Nanocrystals

PL:

Fotoluminescência

PMT:

Photomultiplier tube

QFRS:

Quadrature frequency-resolved spectroscopy

SE:

Stretched exponential

SiNCs:

Silicon nanocrystals

TRS:

Time-resolved spectroscopy

Efeito da temperatura nas propriedades mecânicas de nanofibras de PU eletrofiado Desempenho termoelétrico aprimorado de filmes finos epitaxiais com ba-dopagem biCuSeO orientados ao eixo c