Simulação de dinâmica molecular no mecanismo de corte no processo de usinagem híbrida de silício monocristalino

Resumo

Neste artigo, simulações de dinâmica molecular são realizadas para investigar o mecanismo de corte durante o processo de usinagem híbrida combinando os assistentes térmicos e vibratórios. Um modelo de corte modificado é aplicado para estudar o comportamento de remoção de material e a formação de danos subterrâneos em um ciclo de vibração. Os resultados indicam que durante o processo de usinagem híbrida, o mecanismo de remoção de material dominante pode se transformar da extrusão ao cisalhamento em um único ciclo de vibração. Com o aumento da temperatura de corte, a geração e propagação de trincas são efetivamente suprimidas, enquanto o inchaço aparece quando o mecanismo dominante de remoção de material passa a ser o cisalhamento. O mecanismo de formação do dano subsuperficial em um ciclo de vibração pode ser distinto de acordo com a distribuição de tensões. Além disso, a geração de vagas na peça fica aparente com o aumento da temperatura, o que é um fenômeno importante no processo de usinagem híbrida.

Introdução

O silício monocristalino é um importante material semicondutor, que tem sido amplamente utilizado em sistemas ópticos infravermelhos, microeletrônicos e optoeletrônicos devido às suas excelentes propriedades ópticas e mecânicas [1, 2]. No entanto, devido à natureza de dureza e fragilidade do silício de cristal único, fratura frágil microscópica e danos subterrâneos podem ser gerados durante a usinagem mecânica. Durante o processo de micro-fresamento, defeitos de lascamento da aresta do tipo interior induzidos por usinagem podem ser gerados na peça [3]. Na usinagem de corte de diamante de cristal único (SPDT), uma camada danificada varia de 200 a 600 nm pode ser formada dependendo dos parâmetros de processamento [4, 5]. Embora a camada de dano subsuperficial possa ser diminuída para cerca de 50 nm por lixamento e polimento. A eficiência da usinagem e a habilidade na fabricação de estruturas complexas são limitadas. Para superar esses problemas, várias tecnologias de usinagem assistiva foram propostas e testadas. Em particular, o corte termicamente assistido (TAC) [6] e o corte assistido por vibração (VAC) [7] têm atraído atenção generalizada devido ao seu extraordinário desempenho de corte.

Para materiais frágeis como o silício de cristal único, a transição frágil para dúctil pode ser promovida quando a temperatura de usinagem é aumentada. Durante o processo de TAC, a peça de silicone é amolecida termicamente, o que provoca a diminuição das forças de corte [8] e da energia específica de corte [9, 10]. Enquanto isso, o recozimento das fases de alta pressão na fase cúbica de silício torna-se aparente quando a temperatura de usinagem é aumentada [11]. Com a seleção apropriada dos parâmetros de usinagem, a superfície usinada desejada com alta pureza de fase e baixo dano subsuperficial pode ser alcançada por TAC [12,13,14]. Além do TAC, o corte assistido por vibração (VAC) é outro método de promoção para obter uma superfície de alta qualidade em silício de cristal único. Essa técnica tem sido aplicada na indústria de manufatura desde 1960 [15]. No desenvolvimento inicial desta tecnologia, apenas um movimento de vibração linear na direção de corte nominal é praticado na usinagem, que é denominado como corte de vibração linear (LVC). Em 1994, o corte elíptico por vibração (EVC) foi proposto por Shamoto e Moriwaki [16]. A seguir, as viabilidades de usinagem de EVC em muitos materiais frágeis como silício [17, 18], carboneto de silício ligado por reação [7], carboneto de tungstênio [19, 20] e aço endurecido [21] foram verificadas. Durante o processo de EVC, o dano subsuperficial pode ser efetivamente suprimido, uma vez que a profundidade de corte transiente (DOC) é muito menor do que o DOC nominal [22]. Além disso, devido à separação em cada ciclo de vibração, as superfícies de contato entre a ferramenta de corte e a peça de trabalho são expostas ao gás ou fluido circundante, que dissipa o calor de corte gerado. Portanto, o desgaste da ferramenta de corte, como adesão e reação termoquímica [23], pode ser suprimido de forma eficaz.

Para melhorar ainda mais a usinabilidade de materiais quebradiços, experimentos de usinagem híbrida (HM) combinando o assistente térmico e de vibração foram conduzidos [24, 25]. Foi descoberto que ao cortar o Inconel 718 pelo método HM, a rugosidade da superfície usinada pode ser efetivamente diminuída [26]. Através de experimentos e simulações do método de elementos finitos (FEM), uma queda substancial das forças de corte e uma qualidade de superfície superior das ligas de titânio podem ser alcançadas durante o processo de HM [27]. Esses resultados demonstram a viabilidade do método HM na usinagem de precisão de materiais frágeis. No entanto, é difícil observar e medir diretamente as variáveis físicas durante o processo de usinagem, uma vez que a ferramenta de corte vibra em alta frequência e a zona de deformação está em alta temperatura. Além disso, na fabricação de superfícies nanométricas, a espessura de remoção de material transiente geralmente varia de sub-nanômetros a alguns nanômetros. Portanto, a representação contínua tradicional do problema, como o FEM, é questionável, uma vez que os efeitos da mecânica quântica se tornam aparentes.

Nos últimos anos, a simulação de dinâmica molecular (MD) tem sido amplamente aplicada em investigações do processo de usinagem assistiva devido às suas vantagens no estudo de processos de corte nanométrico [28,29,30]. Com base em simulações anteriores do TAC [31], quando a temperatura de corte é aumentada, a anisotropia na força de corte, energia de corte específica e tensão de escoamento torna-se mais óbvia. Enquanto isso, a força de cisalhamento na peça é menor em temperaturas de corte mais altas, o que leva a zonas de cisalhamento mais estreitas e maiores magnitudes do ângulo do plano de cisalhamento [32]. Além disso, a taxa de remoção de material pode ser melhorada com o aumento da temperatura de corte, uma vez que mais cavacos são formados [33]. Para o processo EVC, foi descoberto por simulação MD que a tensão compressiva e a tensão de cisalhamento na região de deformação podem ser grandemente diminuídas em comparação com o corte comum [34], o que é vantajoso para supressão de danos subterrâneos. Além disso, o processo EVC mostra um afinamento óbvio dos cavacos de corte, resultando em um aumento na relação entre a espessura do cavaco não cortado e a espessura do cavaco cortado [35]. Além disso, foi desvendado que os parâmetros de vibração, incluindo relações de amplitudes, frequências de vibração e diferenças de fase, têm grande influência no desempenho de remoção de material [34, 36].

Essas conquistas notáveis melhoraram a compreensão do mecanismo de usinagem para o processo de usinagem assistiva. No entanto, para economizar tempo de computação e memória, os sistemas de simulação costumam ser bem pequenos. Em simulações anteriores do processo EVC, as amplitudes de vibração e o DOC nominal são menores que 5 nm [22, 36]. Portanto, a espessura transitória de remoção de material é geralmente menor que 1 nm, o que não descreve o processo real de remoção de material com precisão. Além disso, as simulações de MD do processo de HM não foram relatadas. O mecanismo do processo de remoção de material e formação de dano subsuperficial durante o processo de HM ainda não está claro. Portanto, neste artigo, a simulação MD é realizada para revelar o mecanismo de corte do processo HM. O modelo de corte clássico é modificado para que os parâmetros de vibração sejam muito mais próximos dos valores experimentais, por exemplo, a amplitude de vibração é ampliada para 40 nm com uma velocidade de corte nominal de 3,125 m / s. O mecanismo de remoção de material em um ciclo de vibração e a influência do aumento da temperatura de corte são investigados. A simulação de MD é conduzida pelo famoso Simulador Atômico / Molecular Massivamente Paralelo (LAMMPS) [37]. O software de pós-processamento OVITO [38] é empregado para analisar os resultados da simulação.

Método de simulação

Detalhes do modelo de corte

A Figura 1 mostra o diagrama esquemático do processo EVC, originalmente apresentado por Shamoto et al. [39]. A trajetória da ferramenta pode ser expressa como:
$$ x \ left (t \ right) =A _ {{\ text {c}}} \ sin \ left ({2 \ pi ft} \ right) - vt $$ (1) $$ z \ left (t \ direita) =A _ {{\ text {d}}} \ sin \ left ({2 \ pi ft + \ varphi} \ right) $$ (2)
onde x ( t ) e z ( t ) representam o deslocamento da ferramenta de corte no x e z instruções. A _c e A _d são a amplitude de vibração na direção de corte nominal ( x direção) e a direção DOC nominal (negativo z direção). Parâmetros f , v , φ , e t representam a frequência de vibração, velocidade de corte nominal, diferença de fase e tempo de simulação, respectivamente. O tempo de simulação t _i representa a hora do ponto P _i na trajetória da ferramenta da Fig. 1.

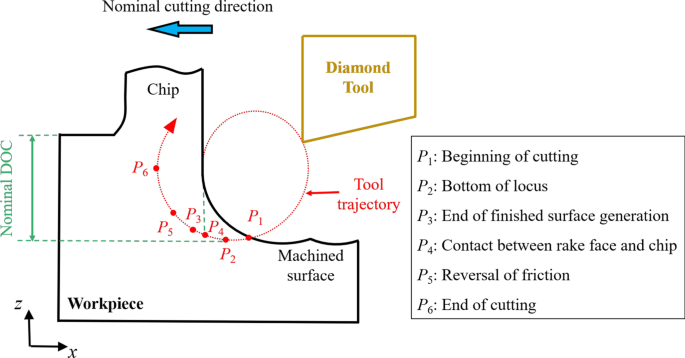
O diagrama esquemático do processo EVC

De acordo com a relação geométrica [40], o valor de t ₁ e t ₃ pode ser determinado por:
$$ x \ left ({t_ {1}} \ right) {-} x \ left ({t_ {3}} \ right) =2 \ pi v / \ omega $$ (3) $$ z \ left ( {t_ {1}} \ direita) {-} z \ esquerda ({t_ {3}} \ direita) =0 $$ (4)
Então, t ₆ pode ser obtido quando a direção do movimento transiente da ferramenta de diamante é paralela à face de inclinação da ferramenta:
$$ \ frac {{A _ {{\ text {c}}} \ sin (2 \ pi ft_ {6}) + v}} {{A _ {{\ text {d}}} \ sin (2 \ pi ft_ {6} + \ varphi)}} =\ tan \ gamma $$ (5)
onde γ é o ângulo de inclinação da ferramenta de corte de diamante.

O modelo MD está presente na Fig. 2. A peça de silicone monocristalino é configurada como corpo deformável. Enquanto a ferramenta de diamante é considerada um corpo rígido, o desgaste da ferramenta pode ser desprezado nesta simulação. A morfologia da peça no modelo de corte clássico é remodelada de acordo com a trajetória da ferramenta no ciclo de vibração anterior, levando em consideração o raio da aresta da ferramenta. A trajetória da ferramenta pode ser determinada conforme ilustrado na Fig. 2b. P _o e P _b são o centro e o ponto inferior do círculo da aresta da ferramenta. Quando o efeito da aresta da ferramenta é considerado, o ponto de geração de superfície transiente P _c varia ao longo da borda da ferramenta durante o movimento da ferramenta. A superfície acabada real é gerada pela linha do envelope da aresta da ferramenta de corte. Se a trajetória de P _b é expresso pelas Eqs. (1) e (2), a trajetória de P _c pode ser calculado através de [41]:
$$ x _ {{\ text {c}}} \ left (t \ right) =A _ {{\ text {c}}} \ sin \ left ({2 \ pi ft} \ right) - vt - r \ sin \ theta \ left (t \ right) $$ (6) $$ z _ {{\ text {c}}} \ left (t \ right) =A _ {{\ text {d}}} \ sin \ left ({ 2 \ pi ft + \ varphi} \ right) + r (1 {-} \ cos \ theta \ left (t \ right)) $$ (7)
Onde
$$ \ sin \ theta \ left (t \ right) =\ frac {{z ^ {{\ prime}} (t)}} {{\ sqrt {x ^ {{\ prime}} (t) ^ {2 } + z ^ {{\ prime}} (t) ^ {2}}}} $$ (8) $$ \ cos \ theta \ left (t \ right) =\ frac {{- x ^ {{\ prime }} (t)}} {{\ sqrt {x ^ {{\ prime}} (t) ^ {2} + z ^ {{\ prime}} (t) ^ {2}}}} $$ (9 )

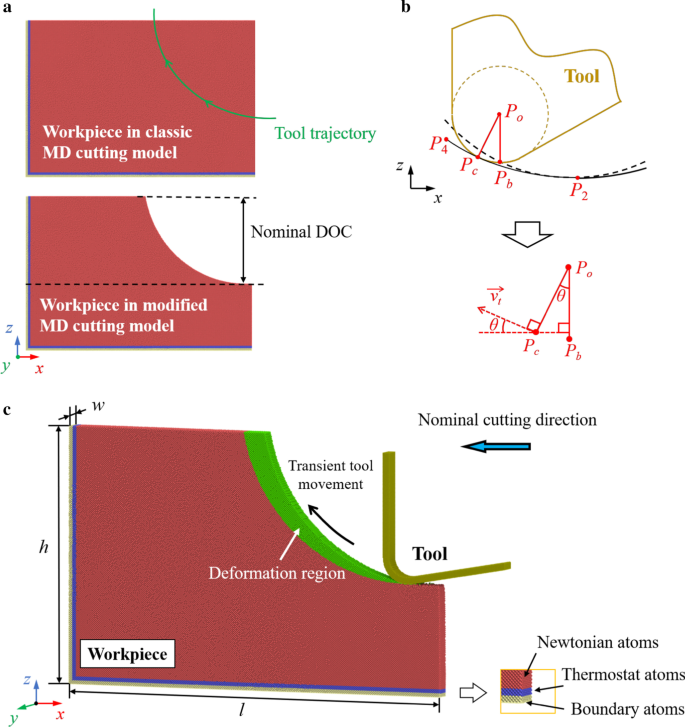
Esquema do modelo de corte MD. a Modificação da peça de trabalho. b Determinação da trajetória da ferramenta. c A morfologia do modelo MD modificado. Os átomos verdes representam a região de deformação em um ciclo de vibração

Os átomos de silício são divididos em três grupos:átomos de fronteira, átomos de termostato e átomos de Newton. Os átomos de limite são fixados em suas posições equilibradas para segurar a peça de trabalho durante a simulação. Os átomos do termostato são mantidos na temperatura ambiente para dissipar o calor de corte gerado, enquanto os átomos newtonianos seguem a segunda lei de Newton.

Os detalhes dos parâmetros de simulação estão listados na Tabela 1. O comprimento l e altura h foram determinados a manter distância suficiente entre a zona de corte e os limites fixos. A condição de limite periódica é aplicada ao longo do y direção para imitar silício em massa. A direção de corte nominal, ângulo de afastamento / inclinação da ferramenta e diferença de fase foram determinados com referência à configuração experimental [42]. A amplitude de vibração e DOC nominal são aumentados para se aproximar da escala experimental com custo de simulação aceitável. Enquanto isso, para garantir a espessura do material removido (átomos verdes na Fig. 2c), a relação de velocidade e a frequência de vibração foram fixadas em 40 e 500 MHz, respectivamente. Portanto, a velocidade nominal de corte foi determinada como 3,125 m / s. Além disso, simulações com diferentes temperaturas de corte são realizadas para revelar o efeito do assistente térmico no mecanismo de corte. A temperatura de corte é aumentada de 300 para 1200 K, o que é realizável durante o TAC como a usinagem assistida por laser [4, 11].

Neste modelo modificado, apenas o estágio de corte durante o ciclo de vibração é simulado e os passos de tempo quando a peça de trabalho é separada com a ferramenta de corte são salvos. Portanto, o poder de computação pode ser concentrado no processo de corte temporário. Mais importante ainda, o processo de remoção temporária de material pode ser descrito com precisão. Uma comparação entre o modelo modificado e o modelo clássico de DM é mostrada na Tabela 2.

Função potencial

Na simulação MD, é importante adotar um potencial robusto para descrever a interação entre os átomos. Para o silício de cristal único, os estudiosos desenvolveram muitos potenciais, como o método do átomo incorporado modificado (MEAM) [45], Stillinger-Weber (SW) [46], Tersoff [47] e muitos corpos com otimização de carga (COMB) [ 48] potenciais. Entre esses potenciais, o potencial analítico de ordem de ligação (ABOP) proposto por Erhart e Albe [49] tem atraído atenção crescente. É uma função potencial de três corpos que permite a formação e quebra de ligações durante a simulação de usinagem. De acordo com pesquisas anteriores [50], o ABOP pode descrever as propriedades do dímero e do volume do silício com precisão. Enquanto isso, as propriedades mecânicas do silício feitas pelo ABOP são consistentes com os experimentos bem [31], o que é importante em simulações MD de usinagem em nanoescala. Portanto, neste artigo, o potencial ABOP é aplicado para descrever as interações silício-silício e carbono-carbono. Enquanto isso, a interação silício-carbono é descrita pelo potencial de Morse, que tem se mostrado um potencial eficiente em simulação de corte em nanoescala [51, 52]. A função potencial de Morse pode ser expressa como:
$$ E _ {{\ text {Si - C}}} \ left ({r_ {ij}} \ right) \, =D _ {{\ text {M}}} \ left [{{\ text {e}} ^ {{- 2a (r_ {ij} - R _ {{\ text {M}}})}} - 2 {\ text {e}} ^ {{- a (r_ {ij} - R _ {{\ text { M}}})}}} \ right] $$ (10)
onde D _M , a, e R _M representa a energia de coesão, o módulo de elasticidade e a distância de equilíbrio entre os átomos, respectivamente. Os parâmetros para o potencial Morse são [53]: D _M =0,435 eV, a =46,487 nm ⁻¹ , R _M =0,19475 nm.

Resultados e discussão

Desempenho de corte

No corte comum, o mecanismo de remoção de material dominante pode ser muito influenciado pela espessura do cavaco não deformada [54]. Com pequena espessura de cavaco não deformada, o mecanismo de remoção de material dominante é a extrusão. A fase metálica estável (Si-II) pode ser gerada pela transição de fase de alta pressão (HPPT), que facilita a deformação dúctil do silício. Quando a espessura do cavaco indeformado é aumentada, o material pode ser removido principalmente por meio do processo de cisalhamento. Enquanto no processo EVC, uma vez que a espessura do cavaco não deformado está constantemente variando, o mecanismo de remoção de material pode se transformar de extrusão para cisalhamento em um ciclo de vibração. A Figura 3 mostra os instantâneos da simulação de corte a 300 K. A estrutura cristalina da peça é determinada pela análise de vizinho comum (CNA) [55]. Esta análise encontra átomos que estão dispostos em uma estrutura de diamante cúbico ou hexagonal. A estrutura não-diamante na Fig. 3c, e contém principalmente a fase amorfa (a-Si), Si-II e outros átomos defeituosos [56]. Essas estruturas são instáveis e se transformarão em a-Si após o corte. Pode-se observar na Fig. 3b, c que o material é removido principalmente por extrusão no estágio inicial de corte. Um ponto de estagnação transitório pode ser observado próximo à aresta da ferramenta de corte. Semelhante ao corte comum, os materiais na região de deformação são divididos pelo ponto de estagnação em cavacos e material comprimido. Conforme a ferramenta de corte prossegue, a espessura do cavaco não deformado é aumentada. Planos de cisalhamento e grãos policristais são gerados na peça, indicando que o cisalhamento se torna o mecanismo de remoção de material dominante.

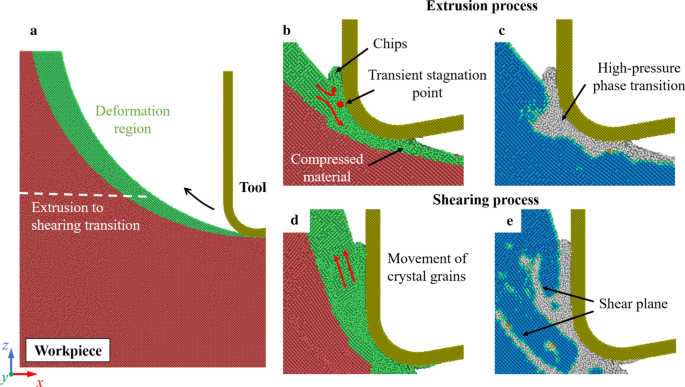
Transição do mecanismo de remoção de material. a Ilustração da região de deformação. b , d Processo de extrusão e cisalhamento. c , e Identificação da estrutura cristalina da peça. Os átomos azuis representam a estrutura do diamante cúbico, enquanto os átomos cinzas estão na estrutura do não diamante

A Figura 4 mostra a morfologia da peça em diferentes temperaturas de corte. Em 300 K, rachaduras e fraturas óbvias podem ser observadas na peça de trabalho durante o movimento para cima da ferramenta. Para materiais frágeis como o silício monocristalino, o movimento ascendente da ferramenta levaria ao arrancamento dos materiais e deixaria defeitos na peça, o que é considerado um problema específico em EVC [42]. Embora essas rachaduras possam ser removidas por outros ciclos de vibração, a estabilidade da usinagem será afetada devido à irregularidade da superfície da peça. Quando a temperatura de corte é aumentada, a geração e propagação de trincas são efetivamente suprimidas. Da Fig. 4d, nenhuma fratura óbvia é detectada quando a temperatura de corte sobe para 1200 K. No entanto, observa-se que em 900 K e 1200 K, o inchaço da superfície usinada torna-se óbvio quando o mecanismo de remoção de material se transforma em cisalhamento. Pode-se concluir que quanto mais grãos de cristal são gerados na fase de cisalhamento, o intumescimento pode ser causado pela rotação desses grãos de cristal em alta temperatura.

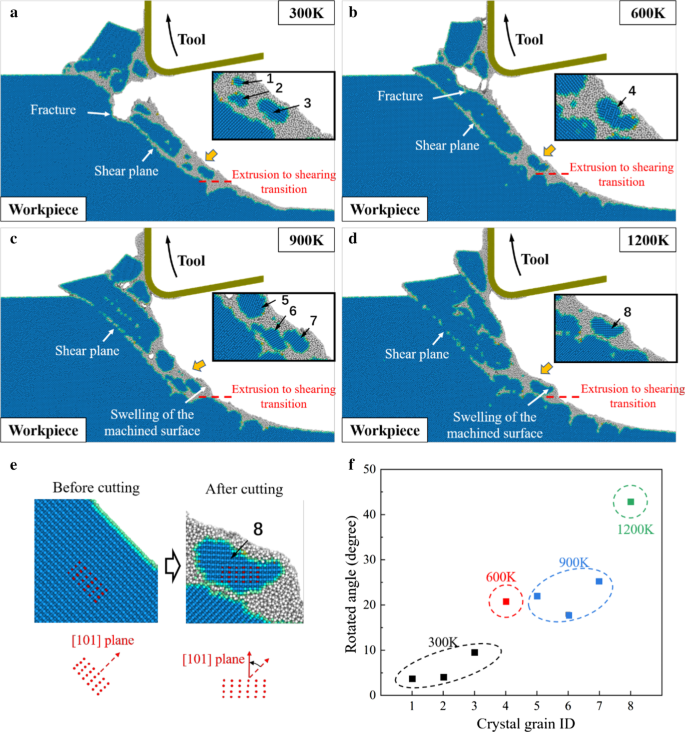
Morfologia da peça de trabalho do processo HM em a 300 K. b 600 K. c 900 K. d 1200 K. Os átomos azuis representam a estrutura do diamante cúbico, enquanto os átomos cinzas estão na estrutura do não diamante. e Determinação do ângulo de rotação de grãos de cristal. f O ângulo de rotação com o aumento da temperatura de corte

Para uma descrição clara dessa rotação, as coordenadas de 24 átomos marcados (átomos vermelhos) nos grãos do cristal são usadas para calcular o ângulo de rotação médio, conforme ilustrado na Fig. 4e. O ângulo de rotação de 8 grãos de cristal (numerados na Fig. 4a-d) é resumido na Fig. 4f. Pode-se observar que o ângulo de rotação é obviamente aumentado em temperaturas elevadas. Durante o processo de HM, a viscosidade de a-Si pode ser bastante diminuída em alta temperatura e o movimento de puxar para cima dos átomos da peça de trabalho é promovido pelo movimento para cima da ferramenta. Portanto, o fluxo atômico na peça é aprimorado e a rotação dos grãos do cristal pode ser facilitada, levando ao inchaço da superfície usinada. Para restringir a rotação dos grãos de cristal, a potência de aquecimento deve ser controlada para evitar o superaquecimento da peça de trabalho. Além disso, os parâmetros de vibração devem ser escolhidos com cuidado, por exemplo, menor velocidade de corte nominal e maior frequência de vibração devem ser aplicadas para suprimir a geração de grãos de cristal e remover o inchaço por mais ciclos de vibração. Conforme ilustrado na Fig. 5, com parâmetros de vibração apropriados, P ₁ poderia localizar no estágio de extrusão e a superfície usinada final é gerada por meio de extrusão sem intumescimento.

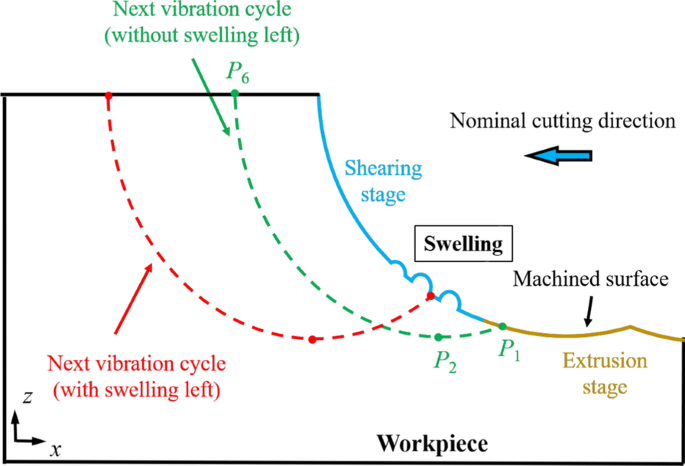
Eliminação do inchaço no processo de HM

Campo de tensão na peça de trabalho

Para investigar melhor o mecanismo de corte durante o processo HM, a distribuição de tensões na peça de trabalho foi calculada. Na simulação MD, a tensão hidrostática pode ser expressa como:
$$ \ sigma _ {{{\ text {hydrostatic}}}} =\, (\ sigma_ {x} + \ sigma_ {y} + \ sigma_ {z}) / 3 $$ (11)
onde σ _x , σ _y e σ _z , são tensores de estresse dos dados de saída do LAMMPS.

A distribuição das tensões hidrostáticas durante os estágios de extrusão e cisalhamento é mostrada na Fig. 6. E os valores de pico das tensões nas regiões de compressão e tração foram marcados. Com o movimento da ferramenta, o ponto de contato entre a ferramenta e a peça varia ao longo do ciclo da aresta da ferramenta, o que resulta no movimento da região compressiva da aresta da ferramenta para a face de saída. Seguindo relatórios anteriores, o HPPT da fase de silício de cristal único (Si-I) para Si-II pode ocorrer em pressões começando em 10-12 GPa [57, 58]. Na simulação de corte a 300 K, a tensão máxima de compressão na extrusão e no estágio de cisalhamento atingiu 18,1 GPa e 17,6 GPa, respectivamente. Este resultado indica que a fase dúctil de Si-II pode ser gerada durante o corte e o HPPT ainda existe na fase de cisalhamento. Além disso, no estágio de extrusão, a tensão de tração concentra-se principalmente perto da área de contato entre a face do flanco da ferramenta e a superfície usinada como resultado da adesão de átomos de silício e a superfície da ferramenta. Conforme a ferramenta avança para o estágio de cisalhamento, a região de tração é ampliada e a concentração de tensão de tração na peça de trabalho subterrânea é muito aumentada, o que é causado pelo movimento de puxar para cima. Quando a temperatura de corte é aumentada, a deformabilidade plástica do silício monocristalino é melhorada e a tensão interna na peça de trabalho é reduzida. Conforme a temperatura aumenta de 300 para 1200 K, a tensão compressiva máxima diminui 16,6% e 25% na fase de extrusão e cisalhamento. Enquanto isso, embora a concentração da tensão de tração na peça de trabalho subterrânea ainda seja óbvia, o valor de pico da tensão de tração é aparentemente diminuído em mais de 30%. Foi relatado que a tenacidade à fratura do silício monocristalino pode ser efetivamente aumentada em temperaturas mais altas [59]. Portanto, rachaduras e fraturas causadas pelo efeito de arrancamento devido ao movimento para cima da ferramenta podem ser suprimidas de forma eficaz.

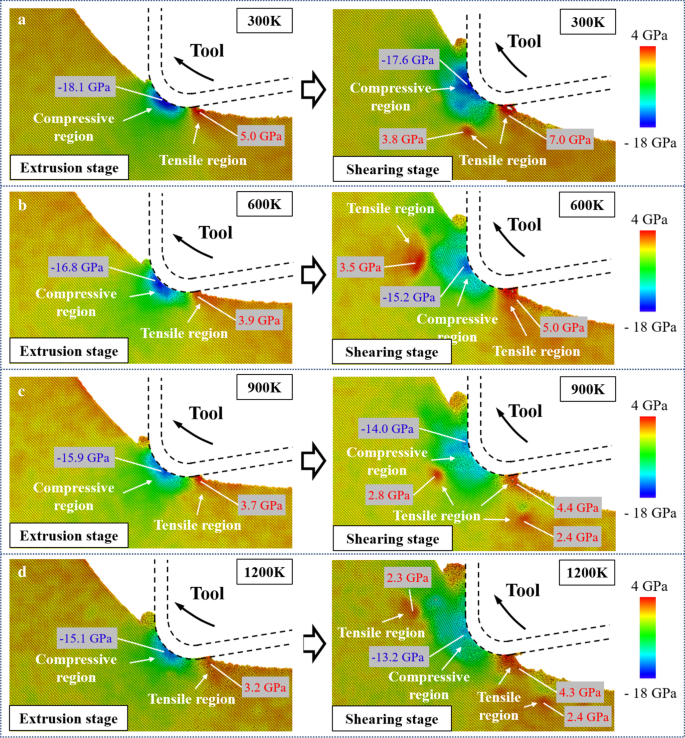
A distribuição da tensão hidrostática em: a 300 K. b 600 K. c 900 K. d 1200 K

O silício de cristal único tem uma estrutura de cristal Face Center Cubic (FCC) com 12 sistemas de deslizamento. Com base no movimento da ferramenta, os principais sistemas de deslizamento para a deformação por cisalhamento são (111) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] e (1 \ (\ stackrel {\ mathrm {- }} {1} \) 1) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] sistemas. Portanto, o componente de tensão de cisalhamento resolvido τ _s no (111) / [\ (\ stackrel {\ mathrm {-}} {1} \) 01] sistema de deslizamento é calculado. Conforme ilustrado na Fig. 7, o componente de tensão de cisalhamento resolvido τ _s na direção M do plano deslizante N pode ser calculado por meio de tensores de tensão por:
$$ \ tau _ {{\ text {s}}} =a_ {1} a_ {2} \ sigma_ {x} + b_ {1} b_ {2} \ sigma_ {y} + c_ {1} c_ {2} \ sigma_ {z} + \ left ({a_ {1} b_ {2} + a_ {2} b_ {1}} \ right) \ tau_ {xy} + \ left ({a_ {1} c_ {2} + a_ {2} c_ {1}} \ direita) \ tau_ {xz} + \ esquerda ({b_ {1} c_ {2} + b_ {2} c_ {1}} \ direita) \ tau_ {yz} $$ (12)
onde a ₁ , b ₁ , c ₁ são os cossenos de direção da direção normal do plano N enquanto a ₂ , b ₂ , c ₂ são os cossenos de direção da direção de deslizamento M . Enquanto τ _xy , τ _xz , e τ _yz são os tensores de tensão de cisalhamento dos dados de saída do LAMMPS.

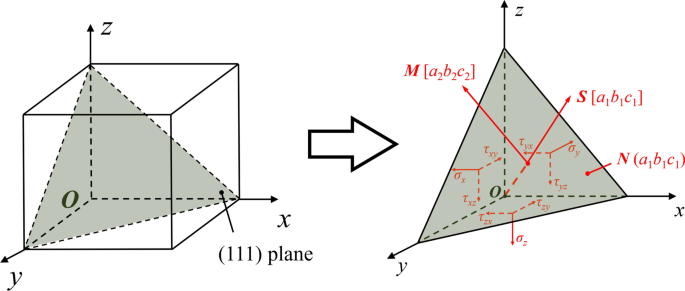
Ilustração dos tensores de estresse

A distribuição da tensão de cisalhamento resolvida τ _s é mostrado na Fig. 8. A região com τ positiva _s é definida como a região de cisalhamento uma vez que o movimento de deslizamento ao longo da direção [\ (\ stackrel {\ mathrm {-}} {1} \) 01] é promovido, o que facilita a remoção do material por cisalhamento. Enquanto a região com τ negativo _s é considerada como a região danificada porque o movimento de deslizamento é preferível na direção oposta, levando à formação de danos subsuperficiais na peça de trabalho. No estágio de extrusão, a tensão na região de cisalhamento é menor do que na região de dano. Danos subterrâneos causados por deformação por cisalhamento podem ser gerados abaixo da superfície usinada [60]. Conforme o movimento da ferramenta de corte, a tensão de cisalhamento ao longo da direção [\ (\ stackrel {\ mathrm {-}} {1} \) 01] é gradualmente aumentada, causando a transição de remoção de material da extrusão para o cisalhamento. Além disso, uma vez que a posição da região danificada se move para cima ao longo do movimento da ferramenta, o dano gerado pode ser removido por meio de um novo ciclo de vibração e não será deixado na peça de trabalho. Quando a temperatura é elevada de 300 K para 1200 K, a tensão de cisalhamento na região de dano diminui 36,1% e 42,4% na fase de extrusão e cisalhamento, respectivamente. Em contraste, devido ao movimento ascendente da ferramenta, a diminuição da tensão de cisalhamento ao longo da direção [\ (\ stackrel {\ mathrm {-}} {1} \) 01] no estágio de cisalhamento é muito menos aparente. A tensão de cisalhamento crítica resolvida (CRSS) para o movimento de deslizamento pode ser expressa como [61]:
$$ \ tau _ {{\ text {c}}} \ left (T \ right) =C \ varepsilon ^ {1 / n} \ exp \ left (\ frac {U} {nkT} \ right) $$ (13 )
onde U e ε representam a energia de ativação do movimento de deslizamento e a taxa de deformação. Parâmetros n e C são constantes materiais. Pode-se concluir que o CRSS pode ser diminuído obviamente com o aumento da temperatura. Portanto, a deformação por cisalhamento na direção [\ ({\ overline {\ text {1}}} \) 01] pode ser facilitada em temperaturas elevadas.

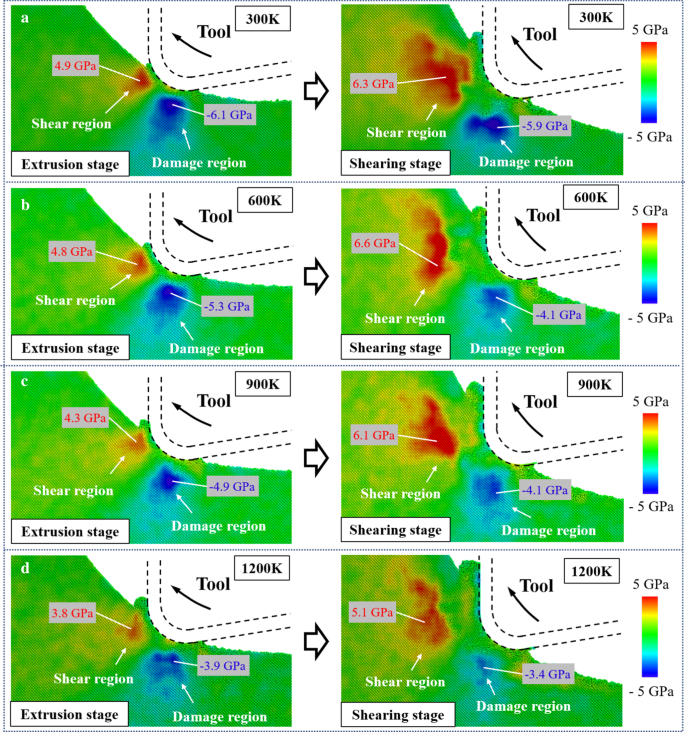
A distribuição da tensão de cisalhamento resolvida em: a 300 K. b 600 K. c 900 K. d 1200 K

Transição de fase

Quando a temperatura de corte é aumentada, a transição de fase do silício pode ser bastante influenciada. O relaxamento do a-Si e a transição para o Si-I podem ser promovidos a uma temperatura adequada [62]. Na Fig. 4, o padrão de dano nas peças de trabalho torna-se mais estreito em altas temperaturas. Uma observação detalhada do padrão de dano ao cortar a 1200 K está presente na Fig. 9a. Observa-se que o dano gerado na região de deformação é parcialmente recuperado após o corte, indicando que ocorreu a transição da estrutura não diamantada para o Si-I. E mais átomos de Si-I são gerados quando a temperatura de corte aumenta, como mostrado na Fig. 9b. Além disso, a malha de superfície construída (cor vermelha) [63] da peça usinada a 1200 K está presente na Fig. 9c. Observa-se que algumas vagas são formadas na peça de subsuperfície. Uma vez que os átomos estão mais compactados na fase Si-I, a transição para Si-I pode causar um encolhimento do material, o que induz vagas na peça de trabalho. O volume das vagas em diferentes temperaturas é calculado e está presente na Fig. 9d. Observa-se que quase nenhuma vaga é gerada à temperatura ambiente. Embora o aumento óbvio das vagas possa ser detectado quando a temperatura de corte aumenta para 900 K e 1200 K.

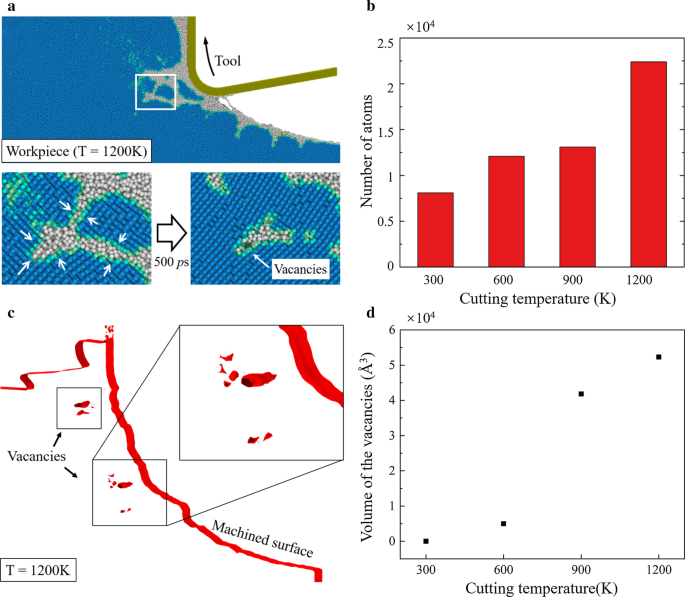
Processo de relaxamento e vagas na peça. a Instantâneo do padrão de dano da peça de trabalho a 1200 K. b Número de átomos transformados da estrutura sem diamante para a fase Si-I. c Malha de superfície construída da peça de trabalho a 1200 K. d O volume das vagas em diferentes temperaturas

Uma análise mais aprofundada das vagas está presente na Fig. 10. Um elemento material abaixo da superfície usinada é escolhido para monitorar a geração de vagas. O número de átomos na estrutura sem diamante e a evolução da tensão do elemento material estão presentes. Conclui-se que durante o processo de corte, o elemento material é inicialmente comprimido e, a seguir, sofre tensão de tração devido ao movimento de subida da ferramenta. Enquanto isso, dois picos da tensão de cisalhamento podem ser observados em 300 K, uma vez que a tensão de cisalhamento na região de dano é aumentada conforme a ferramenta de corte passa. Quando a temperatura de corte aumenta, a diminuição da tensão de cisalhamento é mais óbvia do que a tensão de tração. Em 1200 K, o segundo pico da tensão de cisalhamento quase desapareceu, enquanto a tensão de tração se torna dominante no elemento material durante o processo de relaxamento.

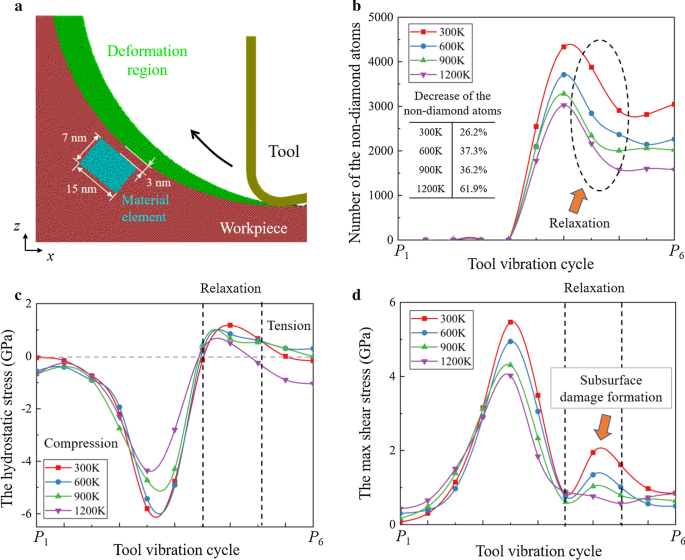
Relaxamento durante o processo de HM. a Ilustração do elemento material. b Estatísticas dos átomos na estrutura não-diamante no elemento material. c , d Evolução do estresse do elemento material

Para explorar o efeito da tensão de tração no processo de formação das vacâncias, simulações de relaxamento de amostra de silício a granel foram conduzidas. Conforme mostrado na Fig. 11a, o modelo inicial é composto de 40% de átomos de Si-I e 60% de átomos de a-Si, que é gerado pelo método de têmpera de fusão [64]. O tamanho do modelo é 21,7 nm × 8,1 nm × 26,1 nm em x , y e z direção, que contém 230.400 átomos. A interface inicial entre a região cristalina e não cristalina é definida como plano de cristal (001). A condição de contorno periódica é aplicada em três dimensões para imitar os materiais a granel. The constructed surface mesh of the relaxed model is present in Fig. 11b. Furthermore, to quantify the vacancies, the solid volume fraction is calculated as the ratio of the solid material volume and the total volume of the simulation sample, as shown in Fig. 11c. It is observed that when temperature is increased, the solid volume fraction decreased obviously under tensile stress. Therefore, to suppress the vacancies, the desired cutting temperature in HM process should be lower than that in ordinary TAC. Meanwhile, the vibration parameters should be optimized to reduce the tensile stress in subsurface workpiece.

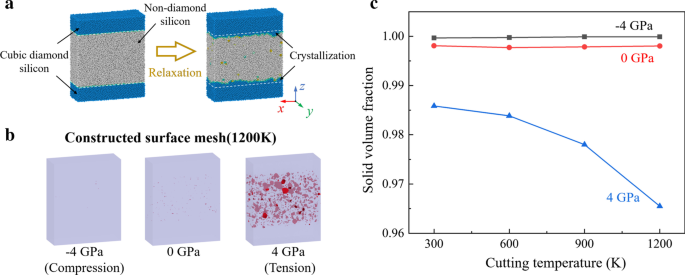
Relaxation simulation of silicon. a Scheme of MD relaxation simulation. b The surface mesh of the relaxed model at 1200 K. c The solid volume fraction curves

Conclusões

In this paper, MD simulation is carried out to investigate the cutting mechanism of hybrid machining (HM) process. A modified cutting model is applied to reveal the material removal behavior and subsurface damage formation in one vibration cycle. The main conclusions were as follows:

(1)
During HM process, the dominant material removal mechanism could transform from extrusion to shear in a single vibration cycle. With an increase of the cutting temperature, the generation and propagation of cracks can be effectively suppressed. However, the swelling appears when the dominant material removal mechanism becomes shearing, which is caused by the rotation of the crystal grains in workpiece.
(2)
Based on the stress analysis, the dominant formation mechanism of the subsurface damage in one vibration cycle can be distinct. In the extrusion stage, the subsurface damage can be generated by the shear stress in the damage region. While in the shearing stage, tensile stress becomes dominant in subsurface damage formation. When the cutting temperature is increased, although the tensile stress concentration in the subsurface workpiece is still obvious, the peak value of the stresses is apparently decreased, which effectively suppress the cracks and fractures in workpiece.
(3)
When the cutting temperature is increased, less subsurface damage is generated in the workpiece. However, due to the tensile stress, some vacancies can be generated in the workpiece when the cutting temperature is increased. Therefore, the desired cutting temperature during HM process should be lower than that in ordinary TAC and the vibration parameters should be set carefully to suppress the vacancies in the subsurface workpiece.

Disponibilidade de dados e materiais

The datasets used and analyzed in the current study can be obtained from the corresponding authors upon reasonable request.

Abreviações

TAC:: Thermal assisted cutting
VAC:: Vibration assisted cutting
LVC:: Linear vibration cutting
EVC:: Elliptical vibration cutting
DOC:: Depth of cut
HM:: Hybrid machining
FEM:: Método do elemento finito
MD:: Dinâmica Molecular
LAMMPS:: Large-scale Atomic/Molecular Massively Parallel Simulator
MEAM:: Modified embedded-atom method
SW:: Stillinger–Weber
COMB:: Charge optimized many-body
ABOP:: Analytical bond-order potential
Si-II:: Metallic stable phase
HPPT:: High-pressure phase transition
CNA:: Common neighbor analysis
a-Si:: Amorphous phase
Si-I:: Single-crystal silicon phase
FCC:: Face Center Cubic
CRSS:: Critical resolved shear stress

Potenciais efeitos osteoindutivos de nanopartículas de hidroxiapatita em células-tronco mesenquimais por interação celular endotelial Uma visão geral sobre o progresso recente de nanobiossensores baseados em óxido metálico / grafeno / CNTs

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias