Impedância de Superfície de Metasurfaces / Estruturas Híbridas de Grafeno

Resumo

Compreender e manipular a impedância de superfície na estrutura híbrida de grafeno é uma questão significativa para aplicações de dispositivos optoeletrônicos baseados em grafeno. Para atingir esse objetivo na região de terahertz, foram derivadas expressões analíticas para as impedâncias da metassuperfície, o que nos permite entender facilmente a relação entre as dimensões físicas e a impedância. Os resultados da simulação mostram uma excelente concordância com as previsões analíticas. Além disso, nos concentramos na impedância sintética quando o patch quadrado e a folha de grafeno se juntam, discutimos a influência do tamanho da metassuperfície, bem como a potencialidade química do grafeno na impedância sintética. Com base nesses resultados, uma série de absorvedores, bem como dispositivos ópticos, podem ser projetados para utilizar metassuperfícies de impedância.

Introdução

Nos últimos anos, novas metassuperfícies de impedância artificial, exibindo propriedades eletromagnéticas anômalas, foram propostas e investigadas nas literaturas anteriores [1,2,3,4,5,6]. Enquanto isso, muitos tipos de aplicações de metassuperfície foram introduzidos, como holografia [1], imagem de alta resolução [2], capa de tapete [3] e absorvedores [4, 5]. Metasurfaces pode desempenhar um papel significativo na compreensão do terahertz fino e dispositivos ópticos. No entanto, devido à resposta dispersiva das metassuperfícies, muitos dispositivos podem funcionar apenas em uma única banda de frequência e o espectro estreito não pode ser sintonizável. Muito recentemente, ao variar a tensão aplicada em uma ampla faixa de frequência, como terahertz ou mesmo frequências ópticas, a condutividade pode ser controlada dinamicamente [7,8,9,10], por isso o grafeno provou ser o melhor candidato para sintonia as características das estruturas plasmônicas e metassuperfícies [11]. Portanto, muitos dispositivos projetados por metassuperfície e grafeno têm sido propostos [12,13,14].

Nesse ínterim, vários modelos analíticos para calcular a impedância equivalente de metassuperfícies ou folha de grafeno têm sido empregados para explicar o mecanismo físico [8, 15,16,17,18,19,20]. Ondas planas usadas para a excitação de modelos de grafeno ou metassuperfície que podem ser divididos em dois métodos diferentes que são analíticos e computacionais. O método computacional é trabalhar na expressão de Floquet [21, 22]. A vantagem de usar esse método é que eles não se restringem à geometria das estruturas, e um dos méritos mais importantes é que ele pode fornecer resultados precisos. No entanto, o software comercial que usa esse método consome tempo e recursos computacionais consideráveis. Por outro lado, um método analítico mais preciso e acurado é desenvolvido [23,24,25,26,27], é fácil de usar e fornece uma melhor análise dos fenômenos físicos. Apesar das vantagens mencionadas acima, os desafios de se obter um modelo analítico de alta precisão para uma unidade de metassuperfície específica também são importantes. Felizmente, esforços e trabalhos consideráveis foram feitos para prever a impedância de superfície equivalente e produziram muitos resultados excelentes [16, 28]. No entanto, para o conhecimento dos autores, o modelo analítico capaz de prever a impedância de superfície desta combinação híbrida ainda não é conhecido.

Neste trabalho, um absorvedor artificial 3D foi utilizado para analisar e predizer a impedância de metassuperfícies / estruturas híbridas de grafeno, que leva em consideração a relação entre metassuperfícies e grafeno. Para o cálculo rápido da impedância superficial das metassuperfícies, as fórmulas analíticas foram inicialmente desenvolvidas. Essas fórmulas analíticas simples e precisas podem permitir uma elucidação completa e requisitos básicos sobre o projeto de impedância. Em seguida, as impedâncias das folhas de grafeno são calculadas. Finalmente, nos concentramos na relação entre o tamanho da metassuperfície, potencial químico μ _c , e a impedância da estrutura composta. Aqui, a impedância de superfície da estrutura híbrida metassuperfície / grafema é discutida calculando seus componentes reais e imaginários. Até onde sabemos, quase não há literatura relatando esse mecanismo de forma abrangente.

Métodos

Impedâncias para retalhos quadrados e folhas de grafeno

Uma estrutura comum de um absorvedor de metassuperfície-grafeno é apresentada na Fig. 1a. Este absorvedor de estrutura simples pode ser facilmente fabricado por microusinagem de superfície. Nesta configuração, uma camada híbrida de metassuperfície-grafeno condutora fina e o plano de aterramento metálico são separados por um substrato dielétrico como um espaçador. A distância ao solo é h . Para um retalho quadrado de tamanho pequeno em comparação com o comprimento de onda (período da matriz D ≪ λ ) e os patches são separados por ranhuras estreitas (largura da ranhura D - w ≪ D ), o presente modelo é válido. De acordo com a teoria da linha de transmissão, um modelo de circuito equivalente da estrutura absortiva pode ser construído (mostrado na Fig. 1b), que pode modelar a metassuperfície-grafeno. Uma linha de transmissão, curto-circuito e a impedância da rede Z _mg , respectivamente, modelam a seção de substrato dielétrico, o plano de aterramento e a impedância de superfície de camadas híbridas de padrão superior. De acordo com a teoria da linha de transmissão, a impedância de entrada Z _em deste absorvedor pode ser estabelecido da seguinte forma:
$$ \ frac {1} {Z_ {in}} =\ frac {1} {Z_1} + \ frac {1} {Z_ {mg}} =\ frac {1} {j {Z} _h \ ast \ tan \ left ({k} _ {zh} h \ right)} + \ frac {1} {Z_ {mg}} $$ (1)

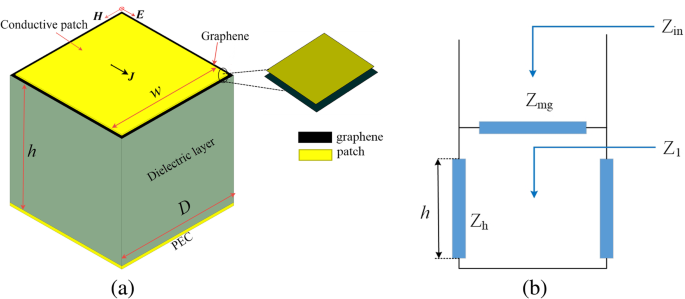
a Esquema da célula unitária do absorvedor de metassuperfície-grafeno. b Modelo de circuito equivalente local

Onde Z _h e k _zh são a impedância das camadas de substrato e a constante de propagação nesta região, respectivamente. Então, a absortividade na incidência normal pode ser calculada por
$$ A \ left (\ omega \ right) =1-R \ left (\ omega \ right) =1 - {\ left | {S} _ {11} \ right |} ^ 2 =1 - {\ left | \ frac {Z_ {in} -120 \ pi} {Z_ {in} +120 \ pi} \ right |} ^ 2 $$ (2)
É óbvio que a impedância da folha metassuperfície-grafeno pode ser extraída do coeficiente de reflexão simulado. A relação entre o tamanho do patch condutor e o potencial químico μ _c pode ser encontrado.

Impedância para retalhos quadrados

Quando a onda plana é perpendicular à metassuperfície, a matriz de manchas planas atua como uma grade capacitiva (como mostrado na Fig. 1a). Impedância de superfície Z _m pode ser ilustrado como as propriedades eletromagnéticas de retalhos quadrados que relacionam a intensidade de corrente média 〈 J 〉 E a intensidade média do campo elétrico 〈 E 〉 No plano do remendo:
$$ \ left \ langle E \ right \ rangle ={Z} _m \ left \ langle J \ right \ rangle $$ (3)
No caso de uma impedância de folha resistiva pura com perdas Z _s (im Z _s =0), na incidência normal a impedância equivalente do patch é representada por Z _m , e pode ser expresso da seguinte forma [9, 18]:
$$ {Z} _m =\ frac {D} {w} {Z} _s-j \ frac {\ eta_ {ef}} {2 \ alpha} $$ (4)
Onde \ ({\ eta} _ {\ mathrm {eff} =} \ sqrt {\ mu_0 / {\ varejpsilon} _0 {\ varejpsilon} _ {\ mathrm {eff}}} \) representa a impedância de onda do hospedeiro uniforme meio e D / w é o elemento geométrico. A permissividade relativa efetiva pode ser aproximada como
$$ {\ varejpsilon} _ {\ mathrm {eff}} \ approx \ frac {\ left ({\ varejpsilon} _r + 1 \ right)} {2} $$ (5)
Além disso, o parâmetro de grade α para uma matriz eletricamente densa de patches condutores idealmente podem ser escritos como
$$ \ alpha =\ frac {k _ {\ mathrm {eff}} D} {\ pi} \ ln \ left (\ frac {1} {\ sin \ frac {\ pi w} {2D}} \ right) $ $ (6)
\ ({k} _ {\ mathrm {eff}} ={k} _0 \ sqrt {\ varejpsilon _ {\ mathrm {eff}}} \) é o número de onda no meio hospedeiro efetivo. No espaço livre, μ ₀ , ε ₀ e k ₀ são a permeabilidade, a permissividade e o número de onda, respectivamente. Além disso, vale ressaltar que a relação (4) é válida quando o comprimento de onda λ é muito maior do que D .

De acordo com a equação (2), podemos descobrir que a impedância equivalente não é determinada apenas pela resistividade da folha de material, mas também pelo período da matriz D e largura w dos parâmetros da estrutura. Para verificar a certeza de tais fórmulas analíticas, os resultados obtidos por simulações de onda completa são apresentados e comparados com as soluções analíticas. A simulação discutida aqui foi realizada usando o software Ansoft HFSS disponível comercialmente. Para obter as características de reflexão da célula unitária do absorvedor de metassuperfície de grafeno, as condições de contorno periódicas e portas Floquet foram implementadas. Durante a simulação, a impedância da folha resistiva pura com Z _s =35 Ω / sq é depositado no substrato com espessura h =20 μm, comprimento D =20 μm, e a permissividade relativa de ε _r =3,2 (1 - j 0,045). Para extrair a impedância do patch Z _m , de acordo com a relação entre a impedância de entrada simulada Z _em e a impedância superficial da placa dielétrica aterrada Z _{g d} , a impedância do patch metassuperfície pode ser expressa da seguinte forma:
$$ {Z} _m =\ frac {Z_ {in} {Z} _ {gd}} {Z_ {gd} - {Z} _ {in}} $$ (7)
Onde Z _gd = jZ _d tan ( k _d h ), \ ({Z} _d =\ sqrt {\ mu_0 / {\ varepsilon} _0 {\ varejpsilon} _r} \) é a impedância característica da laje, \ ({k} _d =\ omega \ sqrt {\ mu_0 {\ varejpsilon} _0 {\ varejpsilon} _r} \) é a constante de propagação ortogonal à superfície do substrato para o modo TEM.

Os resultados analíticos são verificados por comparação com os simulados com base no coeficiente de reflexão extraído, conforme mostrado na Fig. 2. As curvas pretas mostram os resultados simulados enquanto as curvas vermelhas são calculadas usando a expressão analítica proposta. Embora exista uma pequena diferença entre os resultados simulados e as previsões teóricas, isso se deve à Eq. (3) é uma equação aproximada. A tendência geral é a mesma. Assim, confirmando a validade e precisão de nossa expressão analítica para este modelo.

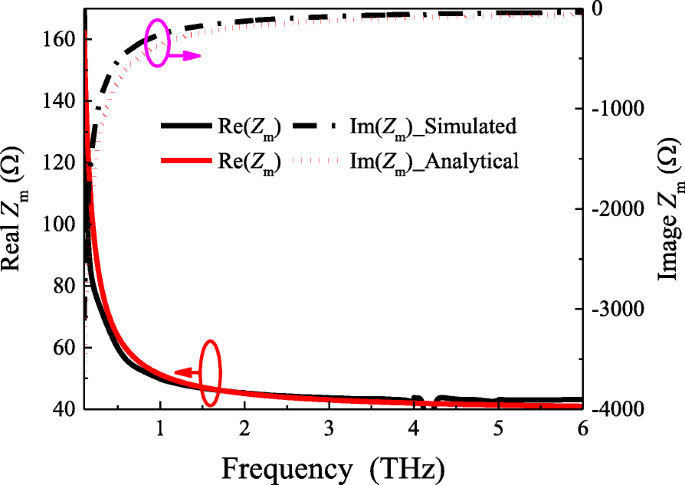
Impedâncias de grade simulada e analítica de patch array com w =19 μm

A fim de investigar o efeito dos tamanhos dos patches na impedância Z _m e validar a eficácia da fórmula (2), realizamos a simulação numérica adicional. A Figura 3 representa as partes reais e imaginárias da impedância da rede Z _m para vários parâmetros geométricos da célula unitária. Da Fig. 3a, pode-se observar que as partes reais da impedância Z _m diminui conforme o parâmetro w aumenta de 17 para 19,5 μm. De acordo com a Eq.2, podemos descobrir que as partes reais de Z _m são inversamente proporcionais ao comprimento do patch w . No entanto, as partes imaginárias mostram a tendência oposta, conforme mostrado nas linhas pontilhadas (mostrado na Fig. 3b). Levando em consideração as Eqs. (2) e (3), as partes imaginárias podem ser dadas por
$$ w \ propto \ ln \ left (\ mathit {\ sin} \ frac {\ pi w} {2D} \ right) \ propto \ frac {1} {\ alpha} \ propto \ operatorname {Im} \ left ( {Z} _m \ right) $$ (8)

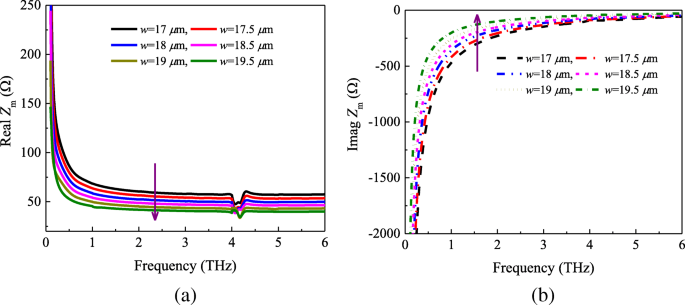
a Real e b parte imaginária da impedância Z _m com diferentes tamanhos de patch

Pela relação (8), sabemos que quando w aumenta de 17 para 19,5 μm, as partes imaginárias da impedância Z _m vai aumentar.

Impedância para folhas de grafeno

O grafeno pode ser visto como uma superfície infinitesimalmente fina. Quando não há polarização magnetostática externa e dispersão espacial, a condutividade da superfície σ _g , pode ser calculado por [29]
$$ {\ sigma} _ {\ mathrm {g}} =\ frac {j {e} ^ 2 {k} _BT} {\ pi {\ mathrm {\ hslash}} ^ 2 \ left (\ omega + j / \ tau \ right)} \ left [\ frac {\ mu_c} {k_BT} +2 \ ln \ left ({e} ^ {- {\ mu} _c / {k} _BT} +1 \ right) \ right] + \ frac {j {e} ^ 2} {4 \ pi \ mathrm {\ hslash}} \ ln \ left [\ frac {2 \ left | {\ mu} _c \ right | - \ left (\ omega + j / \ tau \ right) \ mathrm {\ hslash}} {2 \ left | {\ mu} _c \ right | + \ left (\ omega + j / \ tau \ right) \ mathrm {\ hslash}} \ right] $$ (9)
Onde ℏ é a constante de Planck reduzida, e é a carga de um elétron, k _B é a constante de Boltzmann, enquanto μ _c , ω , τ e T são o potencial químico, a frequência angular, o tempo de relaxamento e a temperatura, respectivamente. Aqui, assumimos T =300 K e τ =0,1 ps em todo este estudo. A impedância da folha de grafeno pode ser calculada como
$$ {Z} _g \ left ({\ mu} _c \ right) =1 / {\ sigma} _g ={R} _g \ left ({\ mu} _c \ right) + j {X} _g \ left ( {\ mu} _c \ right) $$ (10)
Onde R _g e X _g são a resistência e reatância de superfície.

A impedância da folha de grafeno é calculada de acordo com as Eqs. (9) e (10). A Figura 4 indica os componentes reais e imaginários da impedância de superfície versus produtos químicos μ _c . Podemos descobrir que a resistência e reatância da superfície diminuem continuamente com o aumento de μ _c . Além disso, as partes reais da resistência da superfície da folha de grafeno mantêm-se quase inalteradas na faixa de 0,2-6 THz quando o potencial químico é fixado em um certo valor.

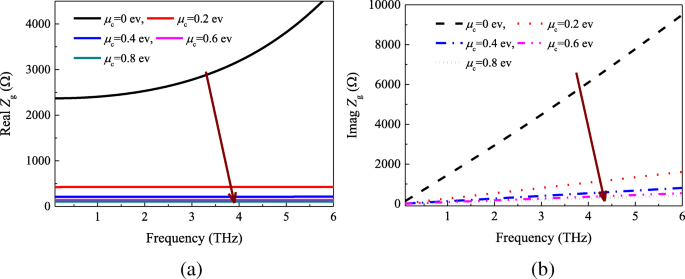
a Real e b partes imaginárias da impedância de superfície em função da frequência e potencial químico

Resultados e discussão

No caso de um patch quadrado em uma folha de grafeno, a impedância de superfície para esta estrutura híbrida deve ser determinada. Nas literaturas anteriores [8, 30,31,32,33,34,35,36,37], a impedância total na superfície desta estrutura híbrida Z _mg é igual à combinação paralela da impedância do patch quadrado Z _m e a impedância da folha de grafeno Z _g , ou seja, Z _mg = Z _m ∥ Z _g . No entanto, através de nossa simulação e cálculo, descobrimos que esta relação não é válida. Para verificar a autenticidade, simulamos uma unidade absorvedor de metassuperfície de grafeno mostrada na Fig. 1a, em seguida recuperamos a impedância superficial do filme de acordo com a Eq (1). A Figura 5 mostra os valores analíticos e simulados da parte real e imaginária de Z _mg em diferentes potenciais químicos com w =19 μm.

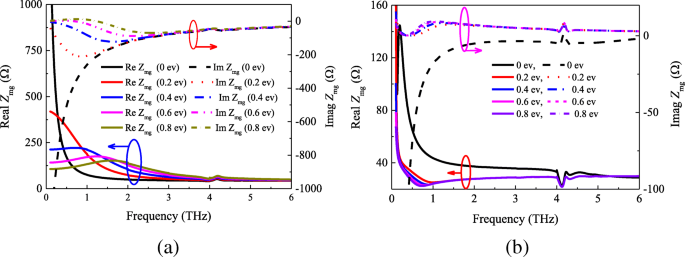
Impedância de filme de metassuperfície-grafeno Z _mg com diferentes potenciais químicos. a Analítico e b resultados simulados

Da Fig. 5a, b, pode-se ver que existem grandes diferenças entre os resultados analíticos e simulados. A Figura 5a mostra que a parte real dos resultados analíticos estava concentrada principalmente entre 40 e 500 Ω, e a parte imaginária da impedância efetiva varia de - 210 a 0 Ω. No entanto, de acordo com a Fig. 5b, podemos encontrar que os valores da parte real da impedância de 20 a 140 Ω, e a parte imaginária é próxima de 0 aumentando μ _c de 0 a 0,8 ev. No entanto, os resultados analíticos e simulados mostram a mesma tendência de que a impedância tenderá a ser estável com o aumento da frequência. A razão é que as impedâncias da folha de grafeno e do retalho quadrado tornam-se menores quando a frequência aumenta. É digno de nota que, comparada a impedância do filme metassuperfície-grafeno a 0 ev com os outros resultados, a impedância Z _mg é bem diferente. Isso se deve aos valores da impedância da folha de grafeno em 0 ev ser bastante diferente do potencial químico mais alto (visto na Fig. 4).

Assim, podemos tirar as seguintes conclusões da impedância calculada e simulada na Fig. 5. Primeiro, a impedância da superfície do filme de metassuperfície-grafeno Z _mg não é estritamente igual à combinação paralela de Z _m e Z _g . No entanto, em segundo lugar, existe uma certa relação entre eles. Para demonstrar essas conclusões, primeiro simulamos a estrutura do absorvedor mostrado na Fig. 1 com tamanhos de remendo variados. O coeficiente de reflexão do absorvedor metassuperfície-grafeno com o potencial químico μ _c =0,4 ev é mostrado na Fig. 6. De acordo com a teoria e modelo da linha de transmissão, a impedância Z _mg pode ser obtido. A Figura 7 mostra os componentes reais e imaginários da impedância recuperada Z _mg com tamanhos de remendo diferentes. De acordo com a Fig. 7a, pode-se ver que a parte real do filme metassuperfície-grafeno diminui no início conforme o comprimento do patch w aumenta de 17 μm para 19,5 μm. No entanto, a tendência oposta é encontrada quando a frequência é superior a 0,31 THz. Por outro lado, a Fig. 7b indica que a tendência da parte imaginária é a mesma que a primeira metade da Fig. 7a. Além disso, comparando as Figs. 4 e 5a, descobrimos que havia uma situação semelhante nas Figs. 3 e 7. Isso também prova diretamente as conclusões acima.

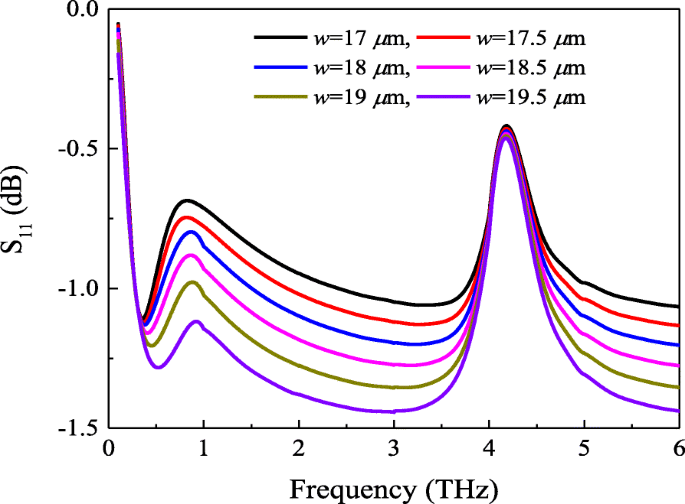
Coeficiente de reflexão do absorvedor de metassuperfície-grafeno com o potencial químico μ _c =0,4 ev

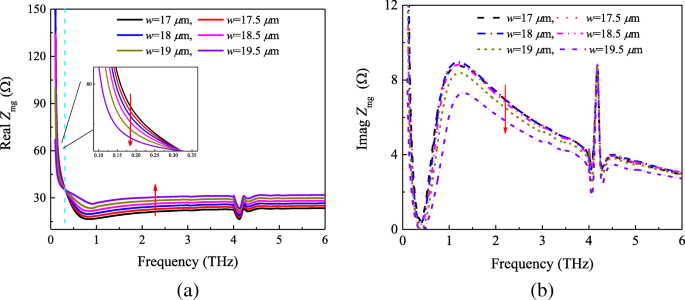
Impedância de filme de metassuperfície-grafeno Z _mg recuperado de S -parâmetros com o potencial químico μ _c =0,4 ev. a Real e b partes imaginárias

Para explorar ainda mais as origens físicas da resistência de superfície em função do tamanho do remendo, as distribuições de corrente de superfície do filme metassuperfície-grafeno em incidência normal são investigadas a 3 THz. A Figura 8 mostra a variação na intensidade da corrente para w =17, 18 e 19 μm com o potencial químico μ _c =0,4ev. A cor representa a intensidade do campo. Obviamente, conforme o tamanho aumenta, a magnitude da corrente de superfície diminui. Levando em consideração a Eq. 3 e Fig. 7a, quando a intensidade do campo elétrico é um valor fixo em 3 THz, a impedância do filme metassuperfície-grafeno pode ser dada por
$$ {Z} _ {mg} \ propto w \ propto \ frac {1} {J} \ kern0,5em \ left (f> 0,32 \ \ mathrm {THz} \ right) $$ (11)

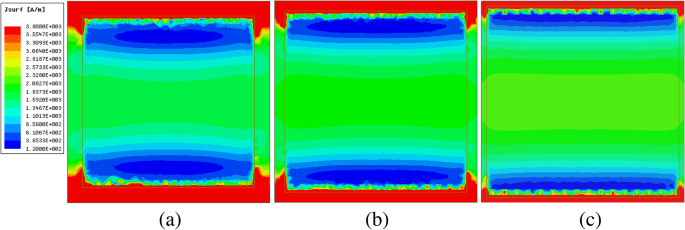
Magnitude da corrente de superfície com diferentes tamanhos de patch, mas na mesma frequência. a w =17 μm, b w =18 μm e c w =19 μm

A partir da relação (11), podemos descobrir que o comprimento do patch é inversamente proporcional à magnitude da corrente de superfície J . A concordância qualitativa entre os resultados simulados e teóricos pode ser observada claramente. Para analisar quantificacionalmente este fenômeno físico, o valor integral da distribuição de corrente de superfície no filme metassuperfície-grafeno é calculado usando a Calculadora de campos HFSS, e os valores são 1.10e-6, 1.07e-6 e 1.04e-6 A , respectivamente. Esses resultados são consistentes com a Fig. 8.

Conclusões

Em resumo, para filmes finos de metassuperfície-grafeno na frequência THz, as impedâncias de superfície fundamental e efetiva foram investigadas. Fórmulas analíticas foram derivadas e verificadas para calcular a impedância de um patch quadrado. Quanto à estrutura híbrida metassuperfície-grafeno, os resultados simulados com base no coeficiente de reflexão extraído foram comparados com os resultados analíticos obtidos a partir da combinação paralela do retalho quadrado e das impedâncias da folha de grafeno. Uma análise adicional foi realizada na discussão do efeito do tamanho do patch na impedância efetiva. Além disso, as relações entre o tamanho do remendo e a impedância do filme foram explicadas qualitativamente e quantificacionalmente pela plotagem e integração da corrente de superfície. Este método de análise pode ser estendido para estudar o problema de impedância com duas outras camadas condutoras diferentes. Além disso, a simulação numérica extensiva, bem como a otimização analítica de camadas compostas especialmente aplicadas à antena e absorvedor, podem ser evitadas por nossa análise feita neste trabalho.

Abreviações

HFSS:: Simulação de estrutura de alta frequência
TEM:: Eletromagnético transversal
THz:: Terahertz

Usando nanopartículas magnéticas carregadas positivamente para capturar bactérias em concentração ultralow Entrega de siRNA à base de micela catiônica para terapia gênica eficiente do câncer de cólon

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias