O efeito de bloqueio de velocidade das partículas em uma camada de grafeno com onda de superfície móvel

Resumo

A difusão rápida induzida por flutuação térmica e vibração foi detectada em nanoescalas. Neste artigo, o movimento de uma partícula em uma camada de grafeno com uma onda de superfície móvel é estudado por simulação de dinâmica molecular e modelo teórico. Está provado que a partícula continuará se movendo na velocidade da onda com certas condições de pré-requisito, ou seja, efeito de bloqueio de velocidade. Ao expressar o potencial de van der Waals (vdW) entre a partícula e a superfície ondulada como uma função das curvaturas, o mecanismo é esclarecido com base na poça de potencial em uma coordenada de quadro de onda relativa. Duas condições de pré-requisito são propostas:a posição inicial da partícula deve se localizar na poça potencial, e a energia cinética inicial não pode conduzir a partícula a pular para fora da poça potencial. A análise paramétrica indica que a região de bloqueio de velocidade será afetada pelo comprimento de onda, amplitude e potencial de par entre a partícula e a onda. Com comprimento de onda menor, amplitude maior e potencial vdW mais forte, a região de bloqueio de velocidade é maior. Este trabalho revela um novo tipo de movimento coerente para partículas em material em camadas baseado na teoria do potencial de poça, que pode ser uma explicação para fenômenos de difusão rápida em nanoescalas.

Introdução

Recentemente, uma série de fenômenos de difusão e transporte rápido induzidos por ondas de superfície / fônons foram detectados em micro / nanoescala. No início, os fenômenos termofóricos ao longo de um nanotubo de carbono [1,2,3,4,5] ou uma fita de grafeno [6,7,8,9,10] foram extensivamente investigados. As flutuações térmicas são confirmadas para permitir o fluxo contínuo de água através de um nanotubo de carbono (CNT), impondo um gradiente térmico axial ao longo de sua superfície [11,12,13]. Simulações de dinâmica molecular de não equilíbrio são feitas para explorar a viabilidade de utilizar um gradiente térmico em um grande substrato de grafeno para controlar o movimento de um pequeno nanofoco de grafeno [6]. Além disso, o transporte térmico de gotas de água em superfícies de grafeno e nitreto hexagonal de boro (h-BN) é estudado por simulações de dinâmica molecular [8, 9]. Sugere-se que esses fenômenos se correlacionam com certos modos de fônons [14,15,16,17,18,19]. Por exemplo, Schoen et al. atribuiu o movimento termofórico dentro de um nanotubo de carbono ao modo de respiração do tubo [1, 20]. Panizon et al. [21] apontaram que as ondas / fônons viajantes de flexão no grafeno podem passar seu momento para os adsorbatos e causar o transporte. Semelhante aos fenômenos termofóricos, Angelos et al. mostraram que as ondulações de propagação induzidas pela temperatura no grafeno podem levar à difusão rápida de nanogotículas de água que é 2-3 ordens de magnitude mais rápida do que a autodifusão de moléculas de água em água líquida [22, 23].

Além da flutuação térmica, estudos confirmam que a vibração também pode transportar partículas e gotículas dentro e fora de um nanotubo de carbono (CNT) [24,25,26,27]. Por exemplo, as nanogotículas são transportadas ao longo do nanotubo com uma velocidade próxima a 30 nm / ns quando ondas acústicas transversais linearmente polarizadas passam o momento linear para a nanogotícula [24, 28]. Guo et al. demonstraram que as moléculas de água dentro de um cantilever vibratório são impulsionadas por forças centrífugas e podem sofrer um fluxo contínuo das extremidades fixas para as livres do CNT por meio de simulações de dinâmica molecular [26, 29]. Um novo transporte unidirecional em nanoescala de moléculas de água através de um nanotubo de carbono de parede única (SWCNT) é projetado usando uma carga de vibração e um SWCNT composto com energia de superfície assimétrica [30]. Zhou et al. [31] investigaram inversões de corrente em uma bomba d'água nanométrica com base em um nanotubo de carbono de parede única alimentado por vibração mecânica e confirmaram que a corrente de água dependia sensivelmente da frequência da vibração mecânica. Chang e Guo [32] descobriram a onda dominó em nanotubos de carbono que pode disparar a molécula interna com grande velocidade de até 1 km / s. Um processo dominó reversível também é comprovado em nanotubos de carbono de parede simples [33].

Como vários fenômenos de difusão e transporte rápidos induzidos por flutuações térmicas e vibração são detectados em nanoescalas, é confirmado que o movimento para cima e para baixo na superfície pode aumentar a difusão e o transporte. A conexão entre o movimento das ondas e das partículas ainda não está clara e não pode ser unificada. Uma explicação principal é que o momento da superfície pode ser transportado para partículas ou gotículas fora da superfície [22, 24]. Mas a relação entre amplitude, frequência e interação entre partícula e superfície não pode ser descoberta a partir desta explicação. Além disso, Angelos et al. apontaram que uma clara preferência por um sinal de curvatura do grafeno é necessária para a difusão rápida do adsorbato na superfície do grafeno [22], o que indica que o potencial de interação induzido pela morfologia da superfície ondulada está intimamente relacionado à difusão rápida. Assim, explorar a interação entre a superfície ondulada e a partícula externa é de fundamental importância para entender o mecanismo de transporte rápido e difusão em nanoescalas.

Neste artigo, ao estudar partícula fora da superfície ondulada de grafeno com base na interação vdW representada pelo potencial do par de Lennard-Jones (L-J), uma relação coerente entre o movimento ondulado e a velocidade da partícula é demonstrada por simulações MD. A velocidade geral da partícula lançada na superfície ondulada é confirmada para se manter a mesma da onda viajante com certas condições de pré-requisito, ou seja, efeito de bloqueio de velocidade. Em seguida, uma teoria da poça de potencial é construída com base no potencial de interação entre a partícula e a superfície da onda expressa em função das curvaturas [34,35,36]. Com esta teoria, duas condições de pré-requisito para o efeito de bloqueio de velocidade são propostas, e a trajetória e a velocidade previstas pela teoria da poça potencial concorda bem com os resultados da simulação MD. Além disso, o efeito do comprimento de onda e amplitude, bem como os parâmetros de interação vdW são analisados, o que mostra boa concordância com a regulação detectada para o fenômeno de surf de gotículas na superfície do grafeno [22]. O mecanismo de efeito de bloqueio de velocidade impulsionado por ondas revela uma nova relação coerente entre a velocidade da partícula e a superfície ondulada.

Métodos

A simulação MD é implementada no pacote de software Large-scale Atomic / Molecular Massively Parallel Simulator (LAMMPS). A superfície ondulada é considerada uma camada de grafeno, que tem uma densidade numérica atômica de \ (\ rho =3,85 \ vezes 10 ^ {19} \, {\ text {m}} ^ {- 2} \). A folha de grafeno é inicialmente plana com z =0 Å e tem 6344 Å de comprimento ao longo de x direção, resultando em um tamanho de célula unitária de 6000 átomos. Ao longo do eixo y a condição de contorno periódica é usada com uma duração de período de 12,2 Å. Aqui, uma partícula esférica é considerada com a massa de \ (m =0,83 \ vezes 10 ^ {- 25} \, {\ text {kg}} \), a fim de simplificar o modelo e focar no efeito geométrico do superfície ondulada. No início, a partícula é colocada em z =7 Å e x =200 Å. Tem uma velocidade inicial de - 50 m / s em z -direcção e cerca de 2.000 m / s em x -direção. Definindo um horário de início para a velocidade inicial em z - direção, a posição inicial pode ser controlada para a partícula que cai na superfície ondulada.

O potencial de ordem de ligação empírica reativa (REBO) é adotado para modelar átomos de grafeno [37]. Enquanto isso, o potencial de Lennard-Jones é escolhido para modelar a interação entre a partícula \ (P \) e cada átomo de carbono no grafeno como,
$$ u \ left (R \ right) =\ varepsilon \ left ({{\ sigma \ mathord {\ left / {\ vphantom {\ sigma R}} \ right. \ kern- \ nulldelimiterspace} R}} \ right) ^ {12} - \ varepsilon \ left ({{\ sigma \ mathord {\ left / {\ vphantom {\ sigma R}} \ right. \ Kern- \ nulldelimiterspace} R}} \ right) ^ {6} $$ (1)
onde \ (\ varepsilon =5,92 \ times 10 ^ {- 21} \, {\ text {J}} \) e \ (\ sigma =4 \ times 10 ^ {- 10} \, {\ text {m}} \). A altura de equilíbrio entre a partícula \ (P \) e a superfície curva é tomada como \ (h =4,2 \ vezes 10 ^ {- 10} \, {\ text {m}} \), decidida pela condição da força normal como zero e resultados de simulação, que são detalhados no arquivo adicional 1:1.

A função de onda progressiva assume uma forma senoidal como,
$$ y =A \ sin \ left ({\ frac {2 \ pi} {\ lambda} x - \ omega t} \ right) $$ (2)
onde a amplitude é tomada como \ (A =1 \ vezes 10 ^ {- 9} \, {\ text {m}} \) e o comprimento de onda é \ (\ lambda =21,75 \ vezes 10 ^ {- 9} \, {\ text {m}} \) salvo indicação em contrário. A frequência angular é tomada como \ (\ omega ={{2 \ pi} \ mathord {\ left / {\ vphantom {{2 \ pi} {10 ^ {- 12}}}} \ right. \ Kern- \ nulldelimiterspace } {10 ^ {- 12}}} \) correspondendo a um período de 10 ps; assim, a velocidade da onda é \ (v _ {{{\ text {wave}}}} =2175 \, {\ text {m}} / {\ text {s}} =\ lambda \ omega / 2 \ pi \) . Para acionar a onda progressiva, os 10 Å esquerdos de grafeno (ou seja, y \ (\ in \) [- 10, 0] Å) é mexido em z -direcção com a amplitude e frequência mencionadas acima. Além disso, átomos de carbono com x > 6010 Å é preso para manter a folha de grafeno estável. Em particular, se uma folha plana de grafeno for simulada, átomos de grafeno não fixados também serão amarrados às suas posições iniciais ao longo de z -eixo com uma constante de mola fraca de 0,0938 eV // Å2 (além de A é definido como 0).

Uma temperatura inicial de 5 K é atribuída a átomos de carbono não fixados. Esta temperatura é definida para eliminar as ondulações termicamente ativadas causadas por um acoplamento harmônico entre os modos de flexão e alongamento do grafeno e focar no efeito da onda viajante causada pela excitação mecânica [22]. A estrutura então evolui em conjunto microcanônico (NVE) com um intervalo de tempo de 1 fs. Monitoramos essa evolução e encontramos a temperatura quase inalterada durante toda a simulação.

Resultados e discussão

A trajetória das partículas na superfície ondulada do grafeno, bem como na superfície plana do grafeno, é ilustrada na Fig. 1. O intervalo de tempo é considerado o período da superfície ondulada. Verifica-se que a posição relativa da partícula não muda em relação às cristas ou vales das ondas, o que significa que a partícula está travada na superfície ondulada com sua velocidade igual à velocidade da onda. Como comparação, o movimento geral da partícula na superfície plana é aparentemente mais lento do que em uma superfície ondulada com a mesma posição inicial. A velocidade da partícula diminui rapidamente na superfície plana devido ao atrito, enquanto o atrito parece não funcionar para partículas na superfície ondulada de grafeno. Mais casos de simulação de MD com diferentes temperaturas de simulação e parâmetros de função de onda são mostrados no arquivo adicional 1:1. As simulações do átomo Xe e da molécula C ₆₀ mover em superfície ondulada e plana são feitas para confirmar a generalização deste fenômeno e mostrado no arquivo adicional 1:2.

As trajetórias de partículas em superfícies onduladas e planas de grafeno

Para entender o mecanismo do efeito de bloqueio de velocidade em nanoescalas, um modelo é construído considerando a interação entre a superfície ondulada S e uma partícula externa P , que é mostrado na Fig. 2a, b. Assumindo que o comprimento de onda e a amplitude da superfície ondulada são \ (\ lambda \) e A , respectivamente, a altura mais próxima entre P e S é h , a densidade numérica de S é \ ({\ rho} _ {s} \). Na simulação MD, a interação entre a partícula P e a superfície ondulada é considerada como interação vdW, que é representada pelo potencial L – J,
$$ U _ {{{\ text {L}} {-} {\ text {J}}}} =\ varepsilon \ left [{\ left ({\ frac {\ sigma} {r}} \ right) ^ { 12} - \ left ({\ frac {\ sigma} {r}} \ right) ^ {6}} \ right] $$

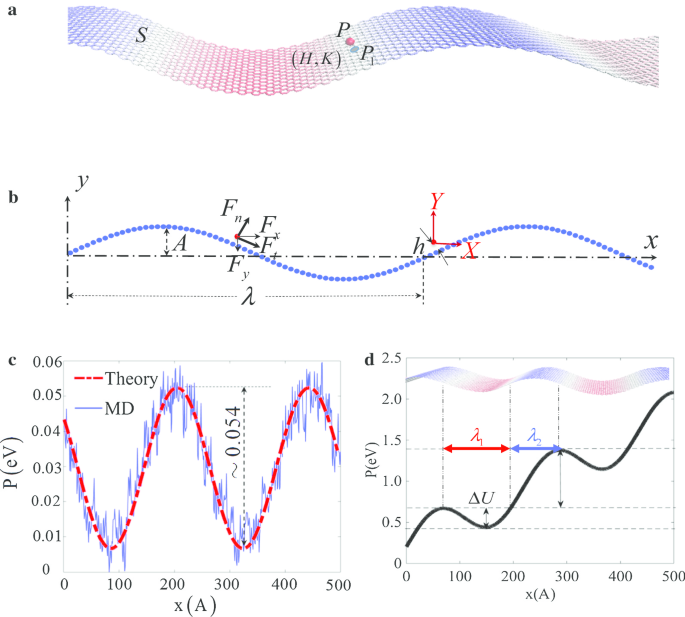
Configurações de geometria e distribuição de potencial. a O modelo 3D da superfície ondulada S e uma partícula externa P com o ponto mais próximo P ₁ na superfície; b o modelo 2D da superfície ondulada S e partícula P ; c a comparação entre os potenciais de interação da superfície ondulada S e uma partícula externa P pela Eq. (1) e simulação de MD; d a distribuição potencial relativa em PXY coordenada

Então, a interação entre P e S provou ser escrito como uma função da curvatura média e da curvatura de Gauss com base no potencial do par L-J [34,35,36],
$$ \ begin {alinhados} U_ {6 - 12} &=\ frac {{4 \ pi \ rho_ {s} \ varepsilon \ sigma ^ {12}}} {{5h ^ {10}}} \ left [{ 1 - hH + h ^ {2} H ^ {2} + \ frac {{9h ^ {2}}} {16} \ left ({H ^ {2} - K} \ right)} \ right] \\ &\ quad - \, \ frac {{2 \ pi \ rho_ {s} \ varepsilon \ sigma ^ {6}}} {{h ^ {4}}} \ left [{1 - hH + h ^ {2} H ^ {2} + \ frac {{3h ^ {2}}} {4} \ left ({H ^ {2} - K} \ right)} \ right] \\ \ end {alinhado} $$ (3 )
Aqui, o ponto \ (P_ {1} \) é o ponto mais próximo na superfície S para a partícula P , e H e \ (K \) são a curvatura média e a curvatura de Gauss no ponto \ (P_ {1} \) (Fig. 2a) [20], respectivamente. Por meio desse potencial baseado na curvatura [Eq. (3)] foi usado para explicar muitos fenômenos anormais em escalas micro / nano [38, 39], a confiabilidade da Eq. (3) neste caso, é validado por comparação com o potencial de superfície na simulação MD para os parâmetros dados acima e exibidos na Fig. 2c.

Antes de analisar a influência da superfície ondulada na partícula P , o atrito deve ser investigado e levado em consideração. O atrito entre as partículas e a superfície da onda pode ser muito complicado em nanoescalas [39,40,41,42,43]. Uma estimativa primitiva do atrito é feita simulando o movimento de uma partícula em uma camada plana de grafeno por MD, conforme detalhado no Arquivo adicional 1:3. Por conveniência, aqui uma superfície plana em vez de ondulada é considerada. Esta aproximação é estimada no arquivo adicional 1:3 combinado com outro mecanismo de poça potencial. Com os parâmetros dados acima, o atrito é estimado como \ (f =- 5,2 \ vezes 10 ^ {- 13} \, {\ text {N}} \).

Então, o potencial relativo entre a superfície S e partícula P é investigado considerando o atrito. Em primeiro lugar, uma coordenada de quadro de onda relativa \ (PXY \) é construída conforme mostrado em vermelho na Fig. 2b, que se move na velocidade da onda, portanto, se mantém estacionária em relação à onda viajante. Portanto, a onda viajante está “congelada” em \ (PXY \). Como a partícula continua se movendo para a direita em relação ao grafeno, o atrito que atua sobre ela será constantemente para a esquerda ao longo da superfície. Como resultado, o potencial relativo da estrutura de onda será o potencial baseado na curvatura menos o trabalho feito por atrito,
$$ P =U_ {n} + f * x $$ (4)
Substituindo o potencial baseado na curvatura U _n e o atrito na Eq. (4), o potencial de quadro de onda relativo pode ser avaliado e é desenhado na Fig. 2d.

Uma vez que a coordenada do quadro de onda PXY se move junto com a onda viajante, a localização inicial da partícula P no potencial determina a trajetória da partícula. Supondo que a velocidade inicial da partícula P é \ (v_ {0} \) e a velocidade da onda é \ (v _ {{{\ text {wave}}}} \), duas condições de pré-requisito podem ser propostas com base na Fig. 2d:a posição inicial da partícula \ ( P \) localiza-se na poça potencial da zona vermelha \ (\ lambda_ {1} \); a energia cinética da estrutura de onda inicial satisfaz \ (\ frac {1} {2} m \ left ({v_ {0} - v _ {{{\ text {wave}}}}} \ right) ^ {2} \ le \ Delta U \). Então, a partícula não será capaz de pular para fora da poça, mas, em vez disso, ficar presa e oscilar dentro da poça. Na perspectiva de uma coordenada absoluta, a partícula \ (P \) irá oscilar na poça potencial, mas continuará se movendo com a propagação da onda pela velocidade travada em torno da velocidade da onda, daí o efeito de travamento da velocidade. Caso contrário, se a localização inicial da partícula \ (P \) cair dentro da zona azul \ (\ lambda_ {2} \) ou a energia cinética inicial relativa \ (\ frac {1} {2} m \ left ({v_ { 0} - v _ {{{\ text {wave}}}}} \ right) ^ {2}> \ Delta U \), a partícula \ (P \) não ficará dentro de uma única poça, mas salta para a esquerda para as poças inferiores ao longo da superfície potencial do quadro de onda. Na perspectiva de uma coordenada absoluta, a partícula ficará para trás da onda de propagação até que outro equilíbrio de forças seja encontrado. Uma possibilidade de tal equilíbrio é que a partícula pare de se mover no grafeno e assim o atrito desapareça. Curiosamente, em lit [21]. Panizon et al. revelam que quando há uma diferença de velocidade, a onda viajante será espalhada pela partícula e oferecerá uma força de propulsão, sugerindo que a velocidade final da partícula será maior que zero.

Para formular e ilustrar melhor nossa teoria, a equação de movimento da partícula P é posteriormente estabelecida pelas leis de movimento de Newton. As forças motrizes exercidas na partícula P incluem duas partes, força normal \ (F _ {{\ text {n}}} \) e força tangencial \ (F _ {{\ text {t}}} \), a saber (Fig. 2b),
$$ F _ {{\ text {n}}} =\ frac {{\ partial U_ {6 - 12}}} {\ partial h}; \, F _ {{\ text {t}}} =\ frac {{\ parcial U_ {6 - 12}}} {\ parcial H} \ nabla H + \ frac {{\ parcial U_ {6 - 12}}} {\ parcial K} \ nabla K $$ (5)
Para o potencial L – J, existem interações atrativas e repulsivas entre os átomos, a partícula externa \ (P \) ficará em uma altura h onde a força normal \ (F _ {{\ text {n}}} \) é zero, o cálculo da determinação da altura h é colocado no arquivo adicional 1:2. Então, a equação do movimento da partícula \ (P \) na direção \ (x \) é,
$$ m \ ddot {x} =F_ {x} - f $$ (6)
Aqui, \ (F_ {x} \) é a componente da força tangencial \ (F _ {{\ text {t}}} \) na direção \ (x \) (Fig. 2b). Calculando a Eq. (6) fornece a trajetória da partícula. Para a superfície da onda senoidal, a curvatura gaussiana é zero e a curvatura média é igual à curvatura da curva na superfície \ (Ozx \), ou seja, \ (K =0 \) e \ (H =\ kappa \) [52], substituindo Eq. (5) em (6), a trajetória móvel da partícula P pode ser resolvido numericamente.

Os exemplos de bloqueio e desbloqueio são mostrados na Fig. 3. Para a localização inicial (Fig. 3a) correspondente à região de bloqueio \ (\ lambda_ {1} \) na Fig. 2d, as trajetórias de resultados teóricos e de simulação MD são comparadas na Fig. 3b. Isso mostra que a partícula para de se mover na superfície plana do grafeno em um tempo muito curto devido ao atrito, enquanto a partícula continua se movendo para a direita na superfície da onda. E a trajetória teórica se aproxima dos resultados da simulação MD. Esta tendência é ainda confirmada na Fig. 3c para a velocidade da partícula mostrada em dez vezes de tempo de simulação. Como a partícula cai na zona de travamento e a velocidade inicial é igual à velocidade da onda, ela oscilará na poça potencial e sua velocidade total será igual à velocidade da onda, o que está de acordo com nossa especulação. Para a partícula com sua localização inicial (Fig. 3d) caindo na região de desbloqueio \ (\ lambda_ {2} \) na Fig. 2d, a trajetória da partícula na superfície da onda tende a uma constante (Fig. 3e) e é confirmada posteriormente pelo distribuição de velocidade. É interessante que a onda progressiva pode aumentar o movimento da partícula mesmo quando cai na região de desbloqueio de velocidade em comparação com o movimento da partícula na superfície plana de grafeno. A Figura 3f ilustra que a velocidade diminuirá a zero por um tempo maior do que o tempo de simulação. Mais exemplos são ilustrados no arquivo adicional 1:3.

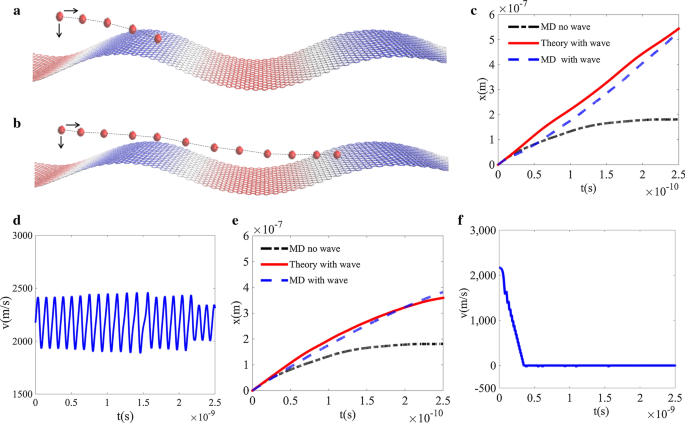
Exemplos de bloqueio e desbloqueio. a Uma visão esquemática que mostra como a partícula pousa na região de bloqueio de velocidade \ (\ lambda_ {1} \) da superfície ondulada do grafeno, onde a velocidade inicial da partícula é \ (v_ {0} =2175 \, {{\ text {m} } \ mathord {\ left / {\ vphantom {{\ text {m}} {\ text {s}}}} \ right. \ kern- \ nulldelimiterspace} {\ text {s}}} \); b uma vista esquemática mostrando como a partícula pousa na região de desbloqueio de velocidade \ (\ lambda_ {2} \) da superfície ondulada de grafeno; c as trajetórias de partículas por simulação e teoria MD, a trajetória de uma partícula em grafeno plano também é traçada para comparação; d a evolução temporal da velocidade da partícula pela Eq. (6); e as trajetórias de partícula por simulação e teoria MD; f a evolução temporal da velocidade da partícula pela Eq. (6)

De acordo com o mecanismo de poça de potencial, o efeito de bloqueio de velocidade da partícula é dominado pela superfície da onda potencial. O efeito dos parâmetros pode ser discutido com base na teoria da poça potencial. Obviamente, isso inclui comprimento de onda \ (\ lambda \), amplitude A , frequência \ (\ omega \) e os parâmetros de potencial L – J. Note-se que o atrito é assumido para permanecer o mesmo em relação a diferentes parâmetros na análise seguinte. As distribuições potenciais para diferentes comprimentos de onda A , amplitude \ (\ lambda \) e o parâmetro de potencial L – J \ (\ varepsilon \) são ilustrados na Fig. 4, respectivamente. A Figura 4a revela que a profundidade potencial da poça diminui com um aumento de \ (\ lambda \), e não haverá faixa de bloqueio de velocidade quando o comprimento de onda exceder um valor crítico. Além disso, como uma frequência mais baixa \ (\ omega \) se relaciona a um \ (\ lambda \) maior, a faixa de bloqueio de velocidade diminui com um aumento de \ (\ omega \). A Figura 4b ilustra que a profundidade potencial da poça aumenta com um aumento de A , e o efeito de bloqueio de velocidade desaparece quando a amplitude é muito pequena. Observa-se que a proporção A / \ (\ lambda \) não deve ser muito grande para evitar danos. Normalmente, tanto \ (\ lambda \) e A aumentam quando a escala da onda ou das partículas aumenta. Para estudar o efeito de escala, mantemos a proporção \ (\ lambda \) / A corrigido e examinar a influência de variação de \ (\ lambda \) ou A . A Figura 4c mostra a diminuição potencial da profundidade da poça rapidamente com um aumento de \ (\ lambda \) ou A . Isso indica que a força motriz baseada na curvatura diminui rapidamente com uma escala crescente, de modo que o efeito de bloqueio de velocidade para partículas desaparecerá na superfície com ondas em grande escala. Para o parâmetro de potencial L – J \ (\ varepsilon \), é confirmado que a região de bloqueio de velocidade será mais ampla quando o potencial de interação do par for forte e o efeito de bloqueio de velocidade desaparecerá quando o potencial de interação do par for fraco (Fig. 4d).

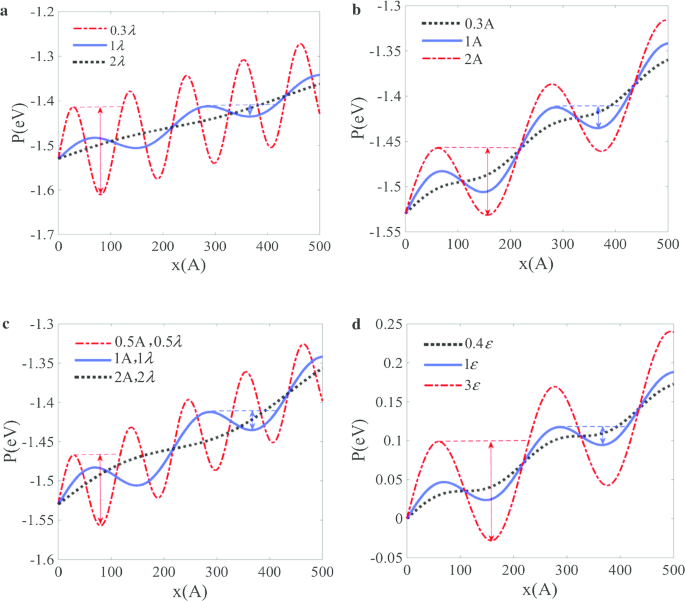
O efeito dos parâmetros na publicação potencial: a o efeito do comprimento de onda; b o efeito da amplitude da onda; c o efeito da razão de comprimento de onda e amplitude; d o efeito do parâmetro potencial L – J

Observa-se que os parâmetros de rigidez e potencial L – J são diferentes para outros nanomateriais 2D, o que leva a diferentes frequências e velocidades de onda [44]. De acordo com a análise de parâmetros, a poça potencial aparecerá ao escolher o comprimento de onda e a amplitude adequados para a superfície ondulada. Como a poça potencial é a pré-condição para partículas que se movem com superfície ondulada, esse efeito de bloqueio de velocidade também se estabelecerá para muitas camadas de nanomateriais 2D sob a interação de curto alcance.

Embora o movimento de uma partícula seja discutido neste artigo, ele ainda está na estrutura do ambiente térmico. A poça potencial é a condição essencial para o movimento de acoplamento entre a partícula e a superfície. Para partículas múltiplas, se todas elas se localizarem na região da poça potencial e satisfizerem as condições de pré-requisito, elas ficarão presas e se moverão com a superfície ondulada. De acordo com o efeito dos parâmetros, o movimento das partículas pode ser controlável ajustando o comprimento de onda e a amplitude. Como a região de bloqueio de velocidade será maior para a onda de superfície com comprimento de onda menor, amplitude maior e frequência mais alta, a difusão rápida na superfície ondulada também será aprimorada. A análise paramétrica também está de acordo com a regulação de difusão rápida detectada em muitas outras literaturas. Por exemplo, Angelos et al. apontaram que o coeficiente de difusão aumenta com a amplitude de ondulação da superfície de grafeno [22]. Eles confirmaram que a amplitude das ondulações aumenta revelando um aumento da preferência das gotas pelos vales, o que pode ser explicado pela Fig. 4b. Quando a amplitude aumenta o suficiente, a região de bloqueio de velocidade provavelmente cobriria todo o comprimento de onda e aumentaria a difusão. Além disso, eles apontaram que o potencial para o vale é sempre menor do que o potencial para a crista [22] (Fig. 4), que está respondendo ao potencial mais baixo para a região da crista mostrada na Fig. 4. Cao et al. estudaram o escoamento do fluido no interior do nanocanal na presença de ondas superficiais viajantes e constataram que a velocidade aumenta com o aumento da amplitude e da frequência [45], o que também está de acordo com a análise paramétrica.

A simulação MD só pode refletir a propriedade em um tempo muito curto, mais aplicações potenciais desse efeito de bloqueio de velocidade podem ser deduzidas do mecanismo de poça potencial. Por exemplo, ao ajustar a amplitude e a frequência, é possível realizar quase travamento ou destravamento da região, que pode fazer com que as partículas se movam ou parem. Observa-se que o movimento ondulado da superfície no sentido vertical pode ser transformado no movimento da partícula no sentido transversal, que se assemelha a uma espécie de movimento de catraca e pode ser utilizado em sistema nanoeletromecânico. Além disso, como a interação entre a partícula e a superfície afetará o movimento, a trajetória potencializada pela superfície ondulada será diferente para partículas com diferentes pares de potenciais, o que pode levar à separação de frases.

Conclusões

Em conclusão, demonstramos uma relação distinta entre partícula e camada de grafeno com a onda de superfície móvel, ou seja, fenômeno de bloqueio de velocidade. Por simulação MD, ele confirmou que a velocidade da partícula pode ser mantida em torno da velocidade da onda com certas condições. Um modelo teórico é construído para elucidar o mecanismo, onde a poça de superfície potencial domina o efeito de bloqueio. As condições de bloqueio são propostas com base neste modelo, ou seja, a posição inicial da partícula localiza-se na poça potencial e a energia cinética inicial não pode conduzir a partícula a saltar para fora da poça potencial. A trajetória da partícula prevista por previsões teóricas concorda bem com os resultados das simulações MD. O efeito do comprimento de onda e amplitude, bem como o parâmetro potencial L – J é discutido. O trabalho também fornece uma nova perspectiva para compreender a difusão e transporte rápidos em superfícies onduladas e as aplicações potenciais para separações de frases.

Disponibilidade de dados e materiais

Todos os dados gerados ou analisados durante este estudo estão incluídos neste artigo publicado [e seus arquivos adicionais].

Abreviações

MD:: Dinâmica Molecular
vdW:: Van der Waals
CNT:: Nanotubo de carbono
h-BN:: Nitreto de boro hexagonal
SWCNT:: Nanotubo de carbono de parede simples
L – J:: Lennard – Jones
LAMMPS:: Simulador Atômico / Molecular Massivamente Paralelo em Grande Escala
REBO:: Ordem de ligação empírica reativa
NVE:: Conjunto microcanônico

Fluxo de água de arquivo único através de membranas nanoporosas bidimensionais Um novo TFET de canal de SiGe sem dopagem e sem dopagem com desempenho aprimorado

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias