Fórmulas matemáticas mágicas para nanoboxes

Resumo

Nanoestruturas ocas estão na vanguarda de muitos empreendimentos científicos. Eles consistem em nanoboxes, nanocages, nanoframes e nanotubos. Nós examinamos a matemática da coordenação atômica em nanoboxes. Essas estruturas consistem em uma caixa oca com n conchas e t camadas externas. As fórmulas mágicas que derivamos dependem de ambos n e t . Descobrimos que as nanoboxes com t =2 ou 3, ou paredes com apenas algumas camadas geralmente têm átomos coordenados em massa. Os benefícios da baixa coordenação em nanoestruturas só ocorrem quando a espessura da parede é muito mais fina do que normalmente sintetizada. O caso em que t =1 é único e tem fórmulas mágicas distintas. Essas nanoboxes de baixa coordenação são de interesse para uma infinidade de aplicações, incluindo baterias, células de combustível, uso plasmônico, catalítico e biomédico. Dadas essas fórmulas, é possível determinar a dispersão superficial das nanoboxes. Esperamos que essas fórmulas sejam úteis para entender como a coordenação atômica varia com n e t dentro de uma nanobox.

Introdução

Nanoboxes foram originalmente sintetizadas por volta de 2002 [1, 2]. Uma nanobox é diferente de uma nanocage porque esta tem paredes porosas. Além disso, ambos são distintos de um nanoframe, em que o nanoframe é uma estrutura (frame) que consiste no contorno de baixa coordenação do cluster. Essas estruturas anisotrópicas e poliédricas podem ser criadas a partir de reações de deslocamento galvânico [3, 4]
$$ \ begin {array} {l} \\ {\ hbox {Ânodo}}:yA _ {(s)} \ rightarrow yA _ {({{\ rm aq}})} ^ {x +} + xye _ {({{ \ rm aq}})} ^ {-} \\ {\ hbox {Cathode}}:xB _ {({{\ rm aq}})} ^ {y +} + xye _ {({{\ rm aq}})} ^ {-} \ rightarrow xB _ {(s)} \\ {\ hbox {Full \, Reaction}}:yA _ {(s)} + xB _ {({{\ rm aq}})} ^ {y +} \ rightarrow yA _ {({{\ rm aq}})} ^ {x +} + xB _ {(s)} \\ \ end {array} $$ (1)
onde um nanocluster com metal A é esvaziado sacrificialmente por uma solução aquosa de metal B , que tem um maior potencial de redução e cria o sólido oco do elemento B . Meias reações ocorrem no ânodo e cátodo de uma célula eletroquímica, resultando na reação combinada completa como acima [5]. Em alguns casos, os cientistas combinaram o deslocamento galvânico com a formação de vazios via difusão Kirkendall Fickiana de metais e vazios [6]. Existem modelos para esta atividade para casos específicos e experimentos de microscopia eletrônica in situ foram relatados [7, 8]. Outros métodos sintéticos incluem corrosão química [9], troca iônica [10] e estruturas metal-orgânicas (MOFs) [11, 12]. Uma revisão recente dos métodos de síntese menciona que os clusters anisotrópicos ainda precisam ser feitos na região de tamanho \ (2
Tais estruturas ocas possuem baixa coordenação, tornando-as de interesse para aplicações em baterias [12], células a combustível [14], plasmônica [15], catalítica [16] e biomédica [17]. Análises anteriores mostram que para aplicações catalíticas, uma abordagem de coordenação se aplica [18], enquanto para armazenamento de energia, existem apenas algumas dicas com os resultados da teoria funcional da densidade (DFT) indicando que algumas facetas são importantes [19]. Usamos um método derivado anteriormente de análise de matriz de adjacência [20, 21] para descobrir a coordenação atômica de uma caixa com n conchas e uma espessura de parede de t camadas. Esta análise mostra que uma nanobox com t =2 ou 3 tem coordenação em massa e, como tal, os benefícios de baixa coordenação estão presentes apenas para nanoboxes com paredes mais finas do que geralmente se acredita necessário. Os métodos que usamos quantificam a coordenação atômica por meio de números mágicos e fórmulas para treze tipos de nanoboxes.

Métodos

A chave para nossa análise por métodos de coordenação é a criação de uma matriz de adjacência a partir das coordenadas atômicas da nanobox. Essa matriz é criada da seguinte maneira. Nós definimos i e j como vizinhos mais próximos, e separe-os do resto exigindo que o comprimento da ligação \ (r_ {ij} $$ {\ mathbf {A}} (i, j) =\ left \ {\ begin {array} {ll} 1 &{\ quad} \ hbox {if} r_ {ij} descreve a matriz de adjacência para o cluster, e
$$ {\ mathbf {E}} (i, j) =\ left \ {\ begin {array} {ll} r_ {ij} &{\ quad} \ hbox {if} \, r_ {ij} descreve a matriz euclidiana da caixa. Usamos a matriz euclidiana para determinar o diâmetro, D , (nm) para as nanoboxes.

Como criamos matrizes de adjacência de vizinho mais próximo, sabemos o número de coordenação \ (\ hbox {cn} _i \) do vértice i somando os elementos de \ ({{\ mathbf {A}}} (i,:) \). Nossa estrutura consiste em \ (n + 1 \) shells numerados 0, 1, ..., n , com t camadas externas. Seja \ (N _ {{\ rm cn} _i} (n, t) \) o número de átomos com coordenação \ (\ hbox {cn} _i \) onde \ (1 \ le \ hbox {cn} _i \ le \ hbox {cn} _M \) com \ (\ hbox {cn} _M \) a coordenação máxima na nanobox. Então, o número total de átomos na nanobox é dado por
$$ N_T (n, t) =\ sum _ {{\ rm cn} _i =1} ^ {{\ rm cn} _M} {N _ {{\ rm cn} _i} (n, t)}. $$ (4)
Os átomos da superfície na camada externa (ou interior) da nanobox, n tem um conjunto de ligações menor do que a coordenação em massa. Assim, a coordenação máxima para átomos de superfície é \ (\ hbox {cn} _s <\ hbox {cn} _M \), e o número de átomos de superfície é
$$ N_S (n, t) =\ sum _ {{\ rm cn} _i =1} ^ {{\ rm cn} _s} {N _ {{\ rm cn} _i} (n, t)}. $$ (5)
Isso é válido se todos os vértices não superficiais tiverem coordenação maior que \ (\ hbox {cn} _s \), o que é verdadeiro para todos os clusters fcc, bcc e hcp. Determinamos o \ (N _ {{\ rm cn} _i} (n, t) \) contando as colunas da matriz de adjacência cuja soma é \ (\ hbox {cn} _i \). Observe que nosso algoritmo de coordenadas de cluster é construído por shells, de modo que cada shell subsequente contém todos os valores inferiores anteriores de n . Além disso, o número de títulos na caixa é
$$ N _ {{\ rm B}} (n, t) =\ frac {1} {2} \ sum _ {{\ rm cn} _i =1} ^ {{\ rm cn} _M} {\ hbox { cn} _i \ cdot N _ {{\ rm cn} _i} (n, t)}, $$ (6)
onde \ (N _ {{\ rm B}} (n, t) \) é o número de ligações e \ (\ hbox {cn} _M \) é a coordenação máxima. O fator 1/2 ocorre por causa da ligação entre pares do vizinho mais próximo.

Já que sabemos que essas equações dependem de n , t como um polinômio de grau no máximo 3, podemos calcular \ (N _ {{\ rm cn} _i} (n, t) \) para 4 valores consecutivos de n , diga \ (n =n_0 + j \), j =0, 1, 2, 3. Um polinômio de interpolação simples fornecerá os coeficientes do polinômio. Deve-se verificar que ao aumentar \ (n_0 \), que geralmente é igual a 1, as fórmulas não mudam. Se as fórmulas se tornam estáveis a partir de \ (n_0 \), então elas valem para todos \ (n \ ge n_0 \). Para obter os coeficientes racionais exatos, é necessário resolver o sistema de Vandermonde para os coeficientes na aritmética exata.

Observe que nas fórmulas mágicas para nanoboxes temos que \ (n> t \) de forma que, portanto, ao contrário de qualquer expectativa, preencher a caixa por uma escolha apropriada de t não recriará as fórmulas mágicas originais para os aglomerados sólidos completos. Essas fórmulas mágicas são úteis para modelar as propriedades de mesoescala de clusters e caixas ou gaiolas. Conjuntos completos de fórmulas foram originalmente derivados para dezenove tipos de cluster. Neste manuscrito, derivamos fórmulas mágicas para treze tipos de nanoboxes.

Nas fórmulas mágicas abaixo, descobrimos que a coordenação em massa pode aparecer para t =2 ou t =3 camadas de espessura de casca. A maioria é para camadas onde t =2; as exceções são o cubo fcc, o cuboctaedro, o icosaedro e o cubo bcc e o cubo truncado. No último, a coordenação em massa só aparece para t =3 camadas. Para os dados abaixo, as tabelas das fórmulas mágicas são acompanhadas por uma figura de uma "meia caixa" para mostrar o interior das nanoboxes. Ao lado está uma barra de cores indicando a coordenação e o número de tais entre parênteses.

Resultados e discussão

Para delinear a aplicabilidade das fórmulas mágicas, delineamos como o comportamento catalítico pode depender da coordenação e de tais fórmulas. Nós definimos G como a energia de Gibbs dependente do tamanho do cluster. Por causa dos adátomos estarem ligados aos átomos da camada externa, há um aumento em G isso é chamado de energia de adsorção e é denotado como \ (\ Delta G \). Isso pode ser dividido em diferentes tipos de coordenação dos átomos na ligação da camada externa com os adátomos. Por exemplo, um átomo de torção é adicionado à energia de adsorção com uma quantidade \ (\ Delta G_ {k} \). Da mesma forma, um átomo de borda adiciona \ (\ Delta G_ {e} \), enquanto um átomo de faceta contribui \ (\ Delta G_f \) então [18]:
$$ \ Delta G =\ sum _ {o \ in \ {f, e, k \}} \ Delta G_o N_o $$ (7)
onde \ (N_o \) é o número de átomos na camada externa do tipo indicado. O número total de átomos na camada externa ligados a adátomos é definido como \ (N_s =N_f + N_e + N_k \), resultando em:
$$ \ begin {alinhados} \ Delta G =&{} \ Delta G_f \ cdot (1-f_e-f_k) + \ Delta G_e \ cdot f_e + \ Delta G_k \ cdot f_k \\ &\ quad {\ hbox {onde} } \, \, f_o =N_o / N_s, \, \, o \ in \ {e, k \}, \ end {alinhado} $$ (8)
com a fração de energia de Gibbs expressa através dos sites de borda e kink que têm coordenadas explícitas para estruturas específicas. Isso demonstra que as fórmulas mágicas têm um papel nas reações de superfície, por meio de coordenadas de arestas e torções e suas fórmulas. Observe que a Eq. (8) aplica-se à adsorção em sites no topo, caso contrário, nem todos os adátomos estarão ligados a átomos na camada externa. Nesse modelo, os sites kink têm fórmulas mágicas que são constantes com o número de cascas, n , os sites de borda têm fórmulas que são lineares com n , e os sites facetados têm fórmulas quadráticas com n . Mais especificamente, os sítios de torção são as fórmulas de coordenação mais baixa, os sítios de borda são a segunda menor coordenada e os sítios de faceta têm cn =8 para (100) facetas e cn =9 para (111) facetas.

Duas relações fundamentais por partícula podem ser aplicadas. Para a energia de Gibbs e constante de adsorção, \ (K _ {{\ rm a}} \), ele contém:
$$ K _ {{\ rm a}} ={\ exp} \ left (- \ frac {\ Delta G} {RT} \ right), $$ (9)
onde R é a constante do gás e T é a temperatura em Kelvin. Além disso, as relações de Brønsted-Evans-Polanyi são amplamente utilizadas na catálise homogênea e heterogênea [18, 22] usando uma relação para constantes de reação k e constantes de equilíbrio K do seguinte modo:
$$ k =gK ^ {\ alpha}, \ quad 0 <\ alpha <1, $$ (10)
onde g e \ (\ alpha \) (parâmetro Polanyi) são constantes. O parâmetro Polanyi não tem unidade e é uma fração própria, como dado originalmente por Brønsted [23]. Então temos:
$$ k =k '_ {a} {\ exp} \ Bigl (- \ alpha \ bigl ({f_n ^ {e} \ cdot \ chi _ {_ e} ({D_n}) + f_n ^ {k} \ cdot \ chi _ {_ k} ({D_n})} \ bigr) \ Bigr), $$ (11)
Onde
$$ \ begin {alinhados} &\ chi _ {_ e} (D) =\ frac {\ Delta G_e (D) - \ Delta G_f (D)} {RT}, \\ &\ chi _ {_ k} (D ) =\ frac {\ Delta G_k (D) - \ Delta G_f (D)} {RT}, \ end {alinhado} $$ (12)
e
$$ k '_ {a} =g \ exp \ left (- \ alpha \ frac {\ Delta G_f} {RT} \ right). $$ (13)
Esta análise mostra que a determinação de um modelo catalítico requer um método de cálculo da energia de Gibbs. Reações catalíticas conhecidas, como os mecanismos de duas etapas e Langmuir – Hinshelwood, foram consideradas [24].

FCC Nanoboxes

Estruturas cúbicas centradas na face são a forma mais comum de nanoclusters e nanoboxes. Essa é a estrutura dos metais com propriedades interessantes, como os metais nobres com propriedades plasmônicas e os metais preciosos catalíticos. Uma vez que o ouro tem um alto potencial de redução de 1,50 V (ver Eq. 1) versus o eletrodo de hidrogênio padrão (SHE) [5], é um dos metais mais fáceis de sintetizar como um nanobox ou nanocage. Nanoboxes ou nanocages de ouro foram formadas em formas cúbicas [1], cuboctaedro [25], icosaedro e decaedro [26], octaedro [27] e tetraedro [28].

Podemos determinar o tamanho aproximado dessas nanoboxes usando uma abordagem de coordenação para o comprimento da ligação do vizinho mais próximo r (cn) [29],
$$ r (cn) =\ frac {2r _ {{\ rm B}}} {\ left (1+ \ exp \ left (\ frac {12 - \ langle cn \ rangle _c)} {8 \ cdot \ langle cn \ rangle _c} \ right) \ right)}. $$ (14)
Aqui, \ (r _ {{\ rm B}} \) é o comprimento da ligação em massa para ouro (0,2884 nm) e \ (\ langle cn \ rangle _c \) é a coordenação média do cluster. Encontramos uma relação linear entre D e n , o número de cascas de cluster, conforme mostrado na Tabela 1:
$$ D (n) =a \ cdot r _ {{\ rm B}} \ cdot n + b. $$ (15)
Usamos nanoboxes com t =3, pois as fórmulas variam com t , e desejamos obter alguma coordenação em massa. Para o cálculo de D ( n ), usamos a distância máxima entre os átomos no cluster, derivada da matriz euclidiana. Observe que D ( n ) é uma fórmula empírica, derivada de dados (variam n e calcular D ), e como tal não está provado.

Essas relações produzem diâmetros de acordo com outros dados, do DFT. Para o cuboctaedra sólido com N igual a 55, 561 e 923, obtemos diâmetros de 1,12 nm, 2,85 nm e 3,43 nm. Isso se compara favoravelmente com os resultados de DFT publicados para 55 átomos de 1,1 nm [30], para 561 átomos, 2,7 nm [31] e para 923 átomos, 3,5 nm [30]. As fórmulas mágicas para algumas nanoboxes fcc são tabuladas abaixo (Tabelas 2, 3, 4, 5, 6, 7, 8).

Nanobaixas icosaédricas e decaédricas

Veja as Tabelas 9 e 10.

Nanoboxes cúbicas de diamante e simples

A estrutura da rede cúbica do diamante é formada por um alótropo de carbono e também pelos elementos silício e germânio. Além disso, alguns compostos cúbicos formam esta estrutura, como óxido de ferro cúbico, diamante tetraédrico maghemita \ (\ gamma \) - Fe ₂ O ₃ . O comprimento da ligação para Fe – O em diamante tetraédrico maghemita \ (\ gamma \) - Fe ₂ O ₃ =0,186 nm [32]. Isso leva ao diâmetro dos aglomerados de diamante D ( n ) como abaixo:
$$ D (n) =3,3984 \ cdot n _ {{\ rm B}} \ cdot n - 0,21194. $$ (16)
De acordo com a referência [12], microboxes de óxido de ferro cúbico se formaram e tiveram interessantes capacidades de armazenamento de lítio. Não temos conhecimento de um modelo de coordenação completo para armazenamento de energia, mas como mencionado acima, os resultados do DFT indicam que a atividade pode depender da orientação das facetas [19]. Nenhum modelo de dependência de armazenamento na coordenação existe atualmente como temos para a catálise. Da equação (16) acima (criada usando t =4), uma microbox requer aproximadamente n =1600 conchas para maghemita de diamante. Fórmulas mágicas para o diamante e estruturas de rede cúbica simples estão listadas abaixo (Tabelas 11, 12).

Nanocaixas BCC

Veja as Tabelas 13, 14 e 15.

Nanocaixas HCP

Consulte a Tabela 16.

O Caso t =1

O caso especial t =1 é único e, como tal, tem fórmulas mágicas distintas. Examinamos este caso para algumas das nanoboxes acima. Nanoboxes com paredes ultrafinas foram formadas com formas cúbicas [33], octaédricas [16] e icosaédricas [34]. De acordo com as fórmulas mágicas abaixo, a nanobox cúbica com t =1 tem a coordenação mais baixa. A platina tem um potencial de redução relativamente alto de 1,18 V em relação ao SHE, portanto, pode ser formada por substituição galvânica, consulte a Eq. (1) [5]. No entanto, as propriedades da reação de redução de oxidação (ORR) de alguns desses nanocages à base de platina indicam que estruturas com (111) facetas em oposição a (100) facetas têm melhores atividades de massa de ORR [35].

Assim, o icosaedro com 20 (111) facetas tem a melhor atividade de massa ORR, seguido pelo octaedro e, por último, o cubo truncado. Esta propriedade do comportamento catalítico da orientação da faceta tendo precedência sobre o número de coordenação é evidenciada pelos dados tabulares abaixo. Em outras palavras, como mencionado nas tabelas a seguir, o cubo com (100) facetas tem os menores números de coordenação mágica com quatro e cinco, ainda que o octaedro e o icosaedro com (111) facetas e fórmulas mágicas maiores tenham melhor atividade de ORR. Esta propriedade é evidenciada também em nanoclusters, onde os resultados de DFT confirmam a dominância das (111) facetas [36], especialmente para ligas de PtNi (Tabelas 17, 18, 19, 20, 21).

Dispersão

Dada a importância dos sítios de borda e torção em relação às facetas no que diz respeito à atividade catalítica, determinamos a dispersão da superfície para algumas das nanoboxes que estudamos. As facetas (100) têm cn =8, enquanto as facetas (111) têm cn =9. Isso pode fornecer uma visão sobre as razões para a atividade poliédrica individual quando comparada entre as nanoboxes. Na Fig. 1 abaixo, traçamos a dispersão da superfície \ (D _ {{\ rm s}} =(N _ {{\ rm e}} + N _ {{\ rm k}}) / N _ {{\ rm S}} \ cdot 100 \% \). Nesta relação, \ (N _ {{\ rm k}} \) é o número de pontos de torção ou canto e \ (N _ {{\ rm e}} \) o número de pontos de borda. Como pode ser visto na Figura 1, nanoboxes com (111) superfícies em oposição a (100) superfícies têm maior dispersão, dando crédito à preferência da atividade catalítica da faceta (111).

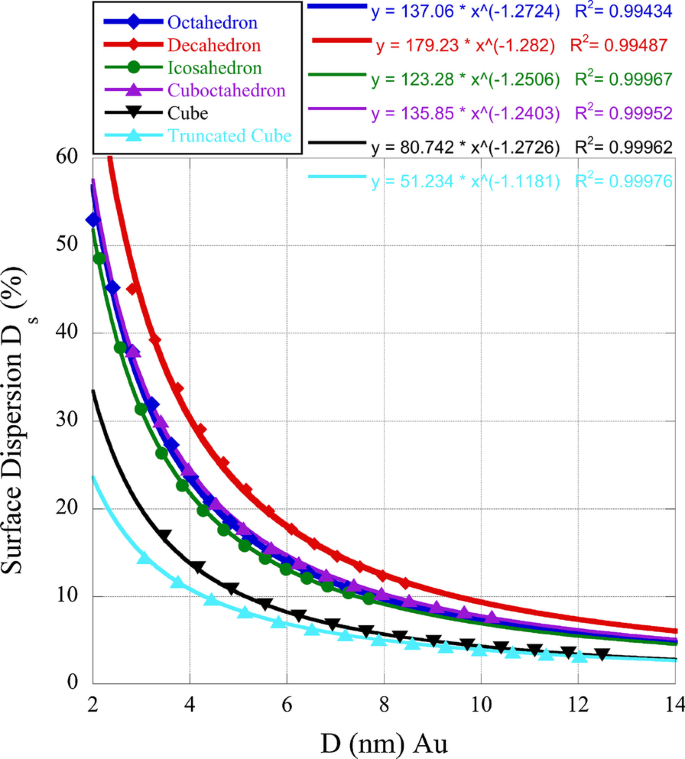
Dispersão de superfície de nanoboxes de ouro

Conclusão

Em resumo, apresentamos a primeira descrição matemática detalhada de fórmulas mágicas para nanoboxes. O caso da espessura da casca, t =1 é diferente de \ (t> 1 \) e tabulamos os dados para alguns desses casos. As fórmulas para a coordenação, número de átomos e número de ligações são enumeradas. Descobrimos que a coordenação em massa aparece para camadas onde t =2 ou 3 e, como tal, é muito mais fino do que normalmente sintetizado. Os benefícios da baixa coordenação são alcançados apenas para paredes muito finas. Esperamos que esses resultados sejam úteis para modelagem e trabalho experimental.

Disponibilidade de dados e materiais

O (s) conjunto (s) de dados que suportam as conclusões deste artigo podem ser obtidos junto ao autor para correspondência.

Abreviações

bcc:: Cúbico centrado no corpo
fcc:: Rosto centrado cúbico
hcp:: Fechado hexagonal
DFT:: Teoria da densidade funcional
SHE:: Eletrodo de hidrogênio secundário

Avaliação quantitativa da internalização celular de nanopartículas poliméricas dentro das células cancerosas da laringe e células do sistema imunológico para a entrega aprimorada de drogas Um fotodetector duplo de quatro quadrantes baseado em silício preto nanômetro aprimorado próximo ao infravermelho

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias