Relações matemáticas mágicas para nanoclusters

Resumo

Propriedades de tamanho e superfície, como catálise, fotoluminescência de pontos quânticos ópticos e ressonâncias de plasmon de superfície dependem da coordenação e da química de nanoclusters de metal e semicondutores. Essas propriedades dependentes de coordenação são quantificadas aqui por meio de "fórmulas mágicas" para o número de conchas, n , no cluster. Investigamos cúbico centrado na face, cúbico centrado no corpo, aglomerados cúbicos simples, aglomerados hexagonais compactados e a estrutura cúbica do diamante como uma função do número de cascas do cluster, n . Além disso, examinamos os sólidos platônicos na forma de clusters de múltiplas camadas, para um total de 19 tipos de cluster. O número de ligações e átomos e números de coordenação exibem características de números mágicos versus n , conforme o tamanho dos clusters aumenta. Começando apenas com as coordenadas espaciais, criamos uma matriz de adjacência e distância que facilita o cálculo de índices topológicos, incluindo os índices de Wiener, hiper-Wiener, Wiener reverso e índices de Szeged. Algumas fórmulas topológicas conhecidas para alguns sólidos platônicos quando n =1 são verificados computacionalmente. Esses índices têm fórmulas mágicas para muitos dos clusters. A estrutura cúbica simples é a menos complexa de nossos clusters, medida pela complexidade topológica derivada do conteúdo de informação da distribuição de grau de vértice. A dispersão, ou porcentagem relativa dos átomos da superfície, é medida quantitativamente em relação ao tamanho e à dependência da forma para alguns tipos de aglomerados com aplicações catalíticas.

Introdução

Números mágicos e fórmulas para nanoclusters têm uma longa história, datando da publicação presciente de van Hardeveld e Hartog em 1969 [1]. Seus insights são anteriores à era da nanociência. Desde então, temos visto números mágicos aparecerem em polígonos 2D e poliedros 3D [2], fulerenos de carbono [3], e em um escopo limitado novamente em clusters [4]. Materiais tão diversos como silício [5], boro [6] e, de fato, mais de 1000 publicações do serviço de indexação “Web of Science” referem-se a números mágicos em clusters. O estudo do tamanho e da forma dos nanoclusters é importante para a sociedade atual, uma vez que determina não apenas as propriedades físicas e químicas intrínsecas, mas também a relevância para aplicações ópticas, catalíticas, eletrônicas e magnéticas [7]. Nosso objetivo é atualizar o banco de dados desse conhecimento com relacionamentos e dados atuais, agora que entramos no reino nano.

A ocorrência de números mágicos em nanoclusters tem a ver principalmente com a formação de camadas de átomos em uma célula fundamental. Quando o número de átomos completa uma camada completa, encontramos um conjunto único de números, denominado “mágica”, que define as camadas dos átomos. Um cluster é representado por um gráfico com os átomos como vértices e as ligações como arestas. Consiste em conchas aninhadas como camadas de uma cebola. Definimos o número de camadas como n e descobrir as relações matemáticas dos números de coordenação do vizinho mais próximo, ligações, o número total de átomos e alguns índices topológicos como uma função de n . O artigo original de van Hardeveld e Hartog [1] considerou os clusters fcc, bcc e hcp. A referência de Teo e Sloane [2] considera poliedros e sólidos platônicos, mas negligencia a relação dos números de coordenação do vizinho mais próximo. Acrescentamos a esse banco de dados observando o cúbico simples, o cúbico de diamante e os sólidos platônicos, além das propriedades topológicas e da dispersão dos aglomerados.

A transição em tamanho de aglomerados para aglomerados de alguns átomos é realmente sobre a relação dos átomos da superfície em comparação com os átomos em massa. Propriedades como química catalítica, ressonância de plasmon de superfície e fotoluminescência de pontos quânticos ópticos [8] são afetadas pela coordenação e número de átomos de superfície. A dispersão ou porcentagem relativa dos átomos da superfície é determinada pela razão entre os átomos da superfície e o número total de átomos, como foi considerado anteriormente [9]. Nossa análise irá determinar a classificação relativa da dispersão em termos de geometria do cluster.

Os índices topológicos começaram com o artigo original de Wiener sobre seu índice e os pontos de ebulição da parafina [10]. Foi só algum tempo depois que Hosoya introduziu um formalismo matemático para analisar índices topológicos [11]. Anteriormente, introduzimos índices topológicos e nanoclusters [12]. Até o momento, existem muitos índices, alguns dos quais dependem da matriz de adjacência ou distância. Mostramos aqui que em muitas das formas de agrupamento, existem relações matemáticas mágicas para os quatro índices como uma função de n e o número de conchas.

Métodos

Para cada um dos tipos de clusters que estudamos, criamos um algoritmo computacional que determina as coordenadas atômicas dos clusters. Em seguida, passamos a criar uma matriz de adjacência e uma matriz de distância definidas a seguir. Uma matriz de adjacência A é criado onde definimos i e j como vizinhos mais próximos e separe-os dos demais exigindo que r _ij < r _c , onde r _c é um valor limite, ligeiramente acima da distância do vizinho mais próximo, mas menor do que a distância do segundo vizinho. Por isso,
$$ \ mathbf {A} (i, j) =\ left \ {\ begin {array} {l} 1 ~~ \ text {if} ~ r_ {ij} onde r _ij é a distância euclidiana entre o átomo i e átomo j . Um valor apropriado para r _c é 1,32 · r _min , onde r _min é o menor comprimento de ligação. Isso se aplica à estrutura dodecaédrica, bem como às outras que estudamos. Os números de coordenação do cluster são simplesmente o número de elementos diferentes de zero em uma coluna da matriz de adjacência. A matriz de distância é definida como
$$ \ mathbf {D} (i, j) =\ left \ {\ begin {array} {ll} 0 &i =j \\ d_ {ij} &i \ neq j \ end {array} \ right. $$ (2)
onde d _ij é o comprimento do caminho mais curto no gráfico de i para j . Existe um algoritmo eficiente para o cálculo da matriz de distância da matriz de adjacência [13]. Usando essas definições, podemos calcular o índice de Wiener, W ( G ), o índice hiper-Wiener, W W ( G ), o índice Wiener reverso rW ( G ), e o índice de Szeged, Sz ( G ), conforme detalhado anteriormente [14]. Esses cálculos usam o mesmo algoritmo que usamos anteriormente para índices topológicos e nanoclusters [12].

Autores anteriores ofereceram provas de relacionamentos mágicos, que condensamos em nossa notação, relevantes para o trabalho aqui apresentado [1, 2]. Como criamos matrizes de adjacência de vizinho mais próximo, sabemos o número de coordenação c n _i do vértice i somando os elementos de A ( eu , :). Nossa estrutura consiste em n Cascas +1 numeradas 0,1,…, n . Seja \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) o número de átomos com coordenação c n _i onde 1≤ c n _i ≤ c n _M com c n _M a coordenação máxima no cluster. Então, o número total de átomos no cluster é dado por
$$ N_ {T} (n) =\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {N _ {{cn} _ {i}} (n)}. $$ (3)
Os átomos da superfície na camada externa n tem um conjunto de ligações menor do que a coordenação em massa. Assim, a coordenação máxima para átomos de superfície é c n _s < c n _M , e o número de átomos da superfície é
$$ N_ {S} (n) =\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {s}} {N _ {{cn} _ {i}} (n)}. $$ (4)
Isso vale se todos os vértices não superficiais têm coordenação maior do que c n _s , o que é verdadeiro para todos os agrupamentos, mas observe a discrepância para o dodecaedro abaixo. Determinamos o \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) contando as colunas da matriz de adjacência cuja soma é c n _i . Observe que nosso algoritmo de coordenadas de cluster é construído por shells, de modo que cada shell subsequente contém todos os valores inferiores anteriores de n . Na Fig. 1, ilustramos as cascas dos aglomerados para um cubo FCC e um dodecaedro. Além disso, o número de títulos no cluster é
$$ N_ {B} (n) =\ frac {1} {2} \ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {{cn} _ {i} \ cdot N _ {{cn} _ {i}} (n)}, $$ (5)
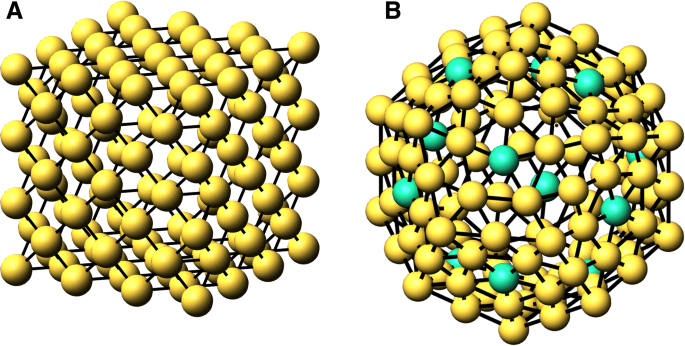
Cascas de átomos para n =3 para A. fcc cubo e n =2 B. dodecaedro. Em B, os átomos verdes (12) referem-se a c n =5 dentro da casca

onde N _B ( n ) é o número de títulos e c n _M é a coordenação máxima. O fator 1/2 ocorre por causa da ligação entre pares do vizinho mais próximo. Esta relação mágica parece não ter sido considerada em publicações anteriores, com exceção de alguns agrupamentos examinados em [4]. Também comentamos que Teo e Sloane derivaram o número total de átomos, átomos de superfície e átomos internos para clusters da seguinte forma [2]:
$$ N_ {T} (n) =\ alpha n ^ {3} + \ frac {1} {2} \ beta n ^ {2} + \ gamma n + 1 ~~ n \ ge {0} $$ ( 6)
onde N _T ( n ) é o número total de átomos, e
$$ \ alpha =C / 6 $$ (7)
onde C é o número de células tetraédricas em que o poliedro é dividido, e
$$ \ beta =1 / 2F_ {s} $$ (8)
onde F _s é o número de faces triangulares na superfície, e
$$ \ gamma =F_ {s} / 4 + V_ {i} + 1-C / 6 $$ (9)
onde V _i é o número de vértices no interior. Eles também mostram que
$$ N_ {S} (n) =\ beta n ^ {2} + 2 ~~ n \ ge {1}; ~~ N_ {S} (0) =1 $$ (10)
e
$$ N_ {I} (n) =N_ {T} (n) - N_ {S} (n), $$ (11)
onde N _eu ( n ) é o número de átomos internos. Esta informação (Eq. (11)) está contida na matriz de adjacência, assim como nas Eqs. (3, 4, 5). Essas equações são uma verificação dos resultados dos dados da matriz de adjacência. Para poliedros centrados, também temos
$$ N_ {I} (n) =N_ {T} (n-1), $$ (12)
e da Eq. (11), temos
$$ N_ {T} (n) =N_ {S} (n) + N_ {S} (n-1) + ... + N_ {S} (1) + N_ {S} (0). $$ (13)
A partir dessas equações, podemos derivar as fórmulas mágicas para cada um dos clusters da seguinte maneira. Depois de calcular a matriz topológica de (0,1) -adjacência A para um cluster com n conchas conforme descrito, sabemos que seu tamanho N = N _T ( n ) indica o número total de átomos. A soma das entradas na coluna i dá o número de títulos c n _i ( n ) para átomo i e contando o número de somas das colunas igual a c n _i ( n ) dá obviamente \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \). Uma vez que sabemos que estes dependem de n como um polinômio de grau no máximo 3, podemos calcular N _T ( n ) e c n _i ( n ) por 4 valores consecutivos de n , diga n = n ₀ + j , j =0,1,2,3. Um polinômio de interpolação simples fornecerá os coeficientes do polinômio. Deve-se verificar que aumentando n ₀ , que geralmente é igual a 1, as fórmulas não mudam. Se as fórmulas se tornarem estáveis ​​a partir de n ₀ ativados, então eles aguardam por todos os n ≥ n ₀ . Em alguns casos, a relação polinomial só é válida para os pares n valores ou os ímpares. Por exemplo, para o dodecaedro rômbico fcc (Tabela 1), as camadas sucessivas têm oito átomos com coordenação 3 quando n ≥2 é par, e nenhum se n é estranho. Em tais casos, relações polinomiais diferentes serão válidas para n uniforme e n ímpar, mas os dados são usados ​​para n = n ₀ + j , j =0,2,4,6 com n ₀ ímpar (por exemplo, n ₀ =1) ou n ₀ mesmo ( n ₀ =2). Para obter os coeficientes racionais exatos, é necessário resolver o sistema de Vandermonde para os coeficientes na aritmética exata usando a caixa de ferramentas simbólica do MATLAB. É assim que as Tabelas 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 e 19 são calculadas. Na próxima seção, determinamos fórmulas mágicas para N _T ( n ), N _B ( n ), e para \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) de acordo com a receita prescrita.

A dispersão (fração exposta, FE) dos átomos de superfície é definida como:
$$ \ text {FE} =\ frac {N_ {S}} {N_ {T}} \ cdot 100 \% $$ (14)
onde N _S é o número de átomos da superfície, e N _T é o número total de átomos [9]. Podemos comparar clusters diferentes, definindo o tamanho relativo do cluster como:
$$ d_ {rel} =b (N_ {T}) ^ {1/3}; ~~ b =d_ {at} ^ {- 1} \ cdot \ left (\ frac {6V_ {u}} {\ pi n_ {u}} \ right) ^ {1/3} $$ (15)
onde d _em é o diâmetro atômico covalente, V _u é o volume da célula unitária, e n _u é o número de átomos na célula unitária. A constante da estrutura cristalina b é igual a 1,105 para clusters fcc e hcp, 1,137 para clusters bcc [1], 1,488 para clusters cúbicos simples e 1,517 para clusters cúbicos de diamante. Como é mostrado acima, a fórmula para FE é uma razão de um quadrático para um cúbico para os clusters e pode ser modelada por um ajuste de curva de lei de potência versus d _rel . A variável d _rel nos permite comparar diferentes clusters uns aos outros sem levar em conta a estrutura do cristal. Para alguns dos aglomerados platônicos, onde não há célula unitária de cristal, usamos \ (N_ {T} ^ {1/3} \) como a variável.

Resultados e discussão

O estudo do tamanho e da forma dos nanoaglomerados de metal evoluiu desde sua infância, há duas décadas. A Tabela 20 mostra alguns progressos relevantes a partir de 2018.

Na Tabela, listamos principalmente metais de transição, não ligas ou compostos, com exceção da bipirâmide hexagonal truncada, onde apenas Fe ₂ O ₃ foi encontrado. Houve mais síntese de clusters de ouro do que qualquer outro elemento, devido às suas propriedades e estabilidade. Nas subseções a seguir, limitamos nossa discussão a tópicos específicos relacionados a fórmulas mágicas e tipos de clusters.

Clusters FCC

Oito dos metais de transição cristalizam na estrutura fcc, consulte a Tabela 21 abaixo, incluindo os metais nobres plasmônicos e importantes elementos cataliticamente ativos. A grande maioria da síntese de nanoaglomerados tem sido feita com esses elementos. As referências da síntese dos elementos fcc com várias formas e tamanhos são fornecidas na Tabela 21.

Ligas desses elementos também são de interesse, mas as referências desses elementos são numerosas demais para serem citadas aqui. Freqüentemente, as formas comuns sintetizadas são cubos, octaedros, cuboctaedros e icosaedros. Normalmente, clusters com (111) facetas são mais fáceis de sintetizar, uma vez que a superfície (111) geralmente tem uma energia menor do que a superfície (100) [7]. Descobrimos para o dodecaedro rômbico FCC que existem fórmulas pares e ímpares. Estes concordam com aqueles em [1], se um substituir o “ n ”Em nossas fórmulas pares por 2 ( m -1). As fórmulas para cuboctaedros fcc listadas em [24] produzem os mesmos números mágicos que os nossos, mas são deslocadas em 1, uma vez que numeram as cascas como n =1,2,… e usamos a numeração n =0,1,…. Nossas fórmulas mágicas concordam com aquelas em [2, 4], e em deferência ao trabalho publicado anteriormente, e na manutenção da continuidade da matemática, usamos a notação [2, 4]. As 5 formas de agrupamento fcc e suas fórmulas mágicas associadas aparecem abaixo.

Clusters BCC

Sete dos metais de transição na tabela periódica têm a estrutura bcc, consulte a Tabela 21. Dos elementos magnéticos Fe, Co e Ni, apenas o ferro é bcc. Nanocubos de ferro parecem ser a única forma de cluster bcc sintetizada até agora [25]. Embora a estrutura em massa do ferro seja bcc, nanoclusters de fcc foram sintetizados [26]. Esta referência também analisa a estabilidade termodinâmica dos clusters. Aqui, apresentamos 5 formas de cluster bcc e suas fórmulas mágicas associadas.

Clusters HCP

Doze metais de transição têm a estrutura hcp, consulte a Tabela 21. No entanto, muitos deles oxidam ou não têm interesse científico convincente para serem sintetizados. No que diz respeito à forma do cluster bipiramidal hexagonal na Tabela 11, clusters de ouro foram sintetizados [27]. A bipiramide hexagonal truncada relacionada parece ter sido formada apenas por α −Fe ₂ O ₃ [28].

Aglomerados platônicos

Os sólidos platônicos são conhecidos desde os antigos gregos. Eles incluem o cubo, tetraedro, octaedro, icosaedro e dodecaedro. Nas tabelas anteriores, listamos fórmulas mágicas para cubos fcc e bcc e octaedros. Aqui listamos as fórmulas para o icosaedro, dodecaedro, tetraedro e tetraedro centrado no corpo. Conforme mencionado anteriormente na seção “Métodos”, o dodecaedro é único para os clusters aqui analisados, em que c n _s =7 refere-se a átomos de superfície e em massa. Mostramos na Fig. 1b que a camada externa contém átomos coordenados quíntuplos e sêxtuplos. Quando uma concha se torna interna, esses átomos coordenados de cinco e seis vezes tornam-se coordenados de sete e oito vezes com ligações a uma concha em ambos os lados. Além disso, os átomos da camada externa seis vezes coordenados são sete vezes coordenados pela ligação com a camada interna. Portanto, há sete vezes a superfície e os átomos coordenados em massa para o dodecaedro. Cada camada na estrutura tem 12 átomos de camada quíntupla, que produzem 12 n −12 átomos sétuplos coordenados em massa. O resto da coordenação sétupla são átomos de superfície.

Foi demonstrado que os nanoclusters de ouro assumem as formas platônicas [29]. Esta referência inclui o cubo, tetraedro, octaedro e icosaedro. Posteriormente, o nanocluster dodecaedro dourado também foi sintetizado [30]. Aqui, mostramos o tetraedro regular, que é "semelhante a fcc" naquele c _M =12 como nas estruturas fcc, e o tetraedro centrado no corpo na Tabela 16, onde os átomos verdes têm ligações simples. As fórmulas mágicas platônicas são apresentadas a seguir.

Aglomerados de diamante cúbico, cúbico simples e decaedro

Os elementos silício e germânio possuem a estrutura cúbica do diamante, bem como o alótropo do carbono do diamante. Em particular, o silício terminado em hidrogênio tem recebido interesse recente. A (100) superfície terminada em hidrogênio, levando a formas cúbicas em aglomerados, foi determinada como tendo a energia mais baixa [31]. A síntese de nanocubos de Si-H de 8-15 nm de tamanho foi alcançada [32]. A Tabela 17 mostra um diagrama dos aglomerados de Si-H terminados em hidrogênio, com átomos de hidrogênio de ligação simples em verde. Se um nanocluster assumir a forma cúbica de diamante, haverá ligações pendentes únicas, que precisam ser passivadas para ajudar a manter a estrutura. Olhando para as fórmulas mágicas, sugerimos que a composição de tais aglomerados de Si-H é \ (\ phantom {\ dot {i} \!} \ Text {Si} _ {8n ^ {3} + 6n ^ {2} -9n +5} \ text {H} _ {12n-8} \), onde n é o número de conchas no cluster. Esses pontos quânticos semicondutores podem ser de interesse para propriedades ópticas, e a variação no intervalo de banda com o tamanho dos clusters terminados em hidrogênio foi determinada como sendo inversamente proporcional ao tamanho do cluster [33].

A estrutura de rede cúbica simples já foi analisada por outros [4], embora sem os detalhes que fornecemos. Já estudamos o d formas de hipercubo dimensional [14]. O polônio é o único elemento que possui a estrutura cúbica simples. É radioativo, o que pode levar a aplicações especializadas. Aqui, apresentamos as fórmulas mágicas do aglomerado de diamante cúbico, cúbico simples e decaédrico.

Fórmulas Topológicas Mágicas

A complexidade estrutural medida em cristais pode nos dar uma ideia da simplicidade ou complexidade da estrutura e o uso adequado pode classificar estruturas relevantes. Para tais classificações, é útil considerar a descrição gráfica da estrutura cristalina, conforme mencionado na seção “Métodos”. A complexidade topológica para estruturas cristalinas é medida pela distribuição do grau de vértice do gráfico, I _vd [34], utilizando o software ToposPro, versão 5.3.2.2 [35]:
$$ I_ {vd} =\ sum_ {i =1} ^ {v} a_ {i} \ cdot {\ text {log} _ {2}} \ {a_ {i}} $$ (16)
onde a _i é o grau (coordenação) do i o vértice e o somatório prosseguem ao longo de todos os v vértices, do gráfico de quociente. Este parâmetro usa um cristal infinito em oposição aos clusters que estamos considerando, mas é útil para medir a complexidade relativa de diferentes estruturas cristalinas. Assim, quanto maior o número, ou quanto mais conteúdo de informação no gráfico, mais complexo ele é. Na Tabela 22, mostramos os valores de I _vd obtido do ToposPro, derivado de arquivos cif para estruturas cristalinas do Crystallographic Open Database. O polônio é o único elemento que cristaliza na estrutura cúbica simples e o valor é zero, ou seja, o gráfico de quociente tem um vértice e arestas zero, de acordo com o que esperamos, que a estrutura cúbica simples é de fato a estrutura menos complexa. O sal, NaCl, também é mostrado, com dois elementos na estrutura cúbica simples, junto com silício na cúbica de diamante, ouro em fcc, ferro em bcc e cobalto em estruturas hcp. Mencionamos que outra medida de complexidade relacionada à entropia de Shannon [34] não é útil porque esta medida para todos os elementos é identicamente zero.

Um método semelhante ao descrito na seção "Métodos" para determinar fórmulas mágicas pode ser aplicado às fórmulas mágicas que descrevem os índices topológicos. Somente aqui, os graus dos polinômios são 7, 8 ou 9, então seus valores por pelo menos 10 n consecutivos -valores precisam ser calculados. Então, um problema de interpolação de grau mais alto dá o resultado. Uma vez que resolver um sistema linear de tamanho 10 × 10 com a caixa de ferramentas simbólica requer algum tempo, todos os coeficientes para os índices topológicos podem ser calculados simultaneamente usando vários lados direitos para obter os coeficientes de todos os polinômios.

As fórmulas mágicas para os índices topológicos são detalhadas nas Tabelas 23, 24 e 25. Os quatro índices que analisamos dependem apenas de n , o número de conchas no cluster. Olhando para os resultados, a rede cúbica simples como a estrutura menos complexa, também tem as fórmulas “mais simples”. Apesar de nossos esforços, não conseguimos solucionar o índice de Szeged de cubos bcc. Nenhuma solução estável foi encontrada. Em geral, as estruturas fcc são mais fáceis de resolver para fórmulas topológicas. Não fomos capazes de resolver nenhuma estrutura hcp e apenas algumas estruturas bcc. Isso pode estar relacionado à complexidade topológica, já que a rede fcc é mais simples do que bcc ou hcp, consulte a Tabela 22. Nas tabelas, fornecemos fórmulas para o cuboctaedro, icosaedro e decaedro. Anteriormente, [12] fornecemos tabelas de dados numéricos para esses índices, com a ressalva de que o cuboctaedro em [12] tinha diferentes números mágicos. Aqui vemos que os dados tabulados podem ser resumidos sucintamente como fórmulas mágicas. Além disso, o grau do polinômio do índice segue as regras do espaço 3D [14]. Alguns índices topológicos para os sólidos platônicos foram publicados anteriormente [36]. A partir desta referência, verificamos o índice de Wiener para todos os cinco sólidos para n =1. O índice de Wiener para linhas de células unitárias da rede fcc foi estudado [37], mas nossos resultados não podem ser comparados uma vez que estudamos clusters.

Dispersão

A porcentagem de átomos de superfície (dispersão, FE) dos vários aglomerados é apresentada na Fig. 2. Nanoclusters de platina são conhecidos por terem atividade catalítica com relação à reação de redução de oxigênio (ORR), que é dependente do tamanho e da forma [38]. Esta referência determinou que os aglomerados cuboctaédricos de platina de 2,2 nm de tamanho tinham atividade de ORR máxima. Também é conhecido que para ligas de PtNi a superfície (111) é preferida para o ORR [39]. Comparamos os aglomerados icosaédricos, octaédricos, decaédricos e cuboctaédricos para FE em um d _rel =7,5 para platina a 2,2 nm. Os aglomerados icosaédricos, octaédricos e decaédricos têm superfícies com (111) faces. Usando as leis de potência na Fig. 2, encontramos para o dado d _rel que o FE para aglomerados icosaédricos é 47,9%, para cuboctaédricos 52,8% e para decaédricos 57,5% e que aglomerados octaédricos têm FE =58,9 % . Assim, com base na forma, os aglomerados octaédricos têm a superfície (111) e o valor mais alto de FE para um tamanho semelhante. Tanto o coeficiente da lei de potência quanto o expoente são relevantes para a determinação de FE para pequenos d _rel . A interpretação matemática do expoente da lei de potência dá o significado físico como a relação da ordenada, FE, com as abscissas, d _rel , ou a mudança percentual relativa de FE para a mudança percentual relativa de d _rel . O coeficiente da lei de potência é simplesmente o valor de FE quando d _rel =1.

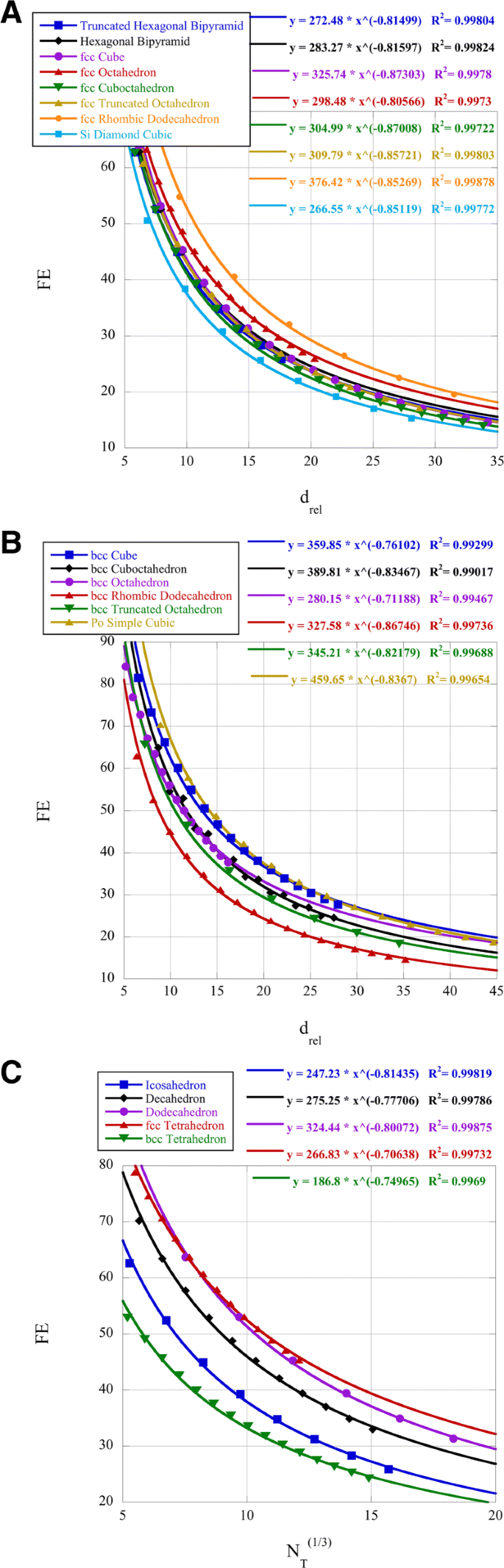
Dispersão FE para os nanoclusters

Outro grupo de pesquisa sintetizou aglomerados icosaédricos de liga de platina e comparou a atividade com octaédricos [40]. Esses nanoclusters tinham cerca de 13 nm de tamanho ou N =20.000 para aglomerados octaédricos e N =15.000 para aglomerados icosaédricos. Isso produz um d _rel =30 para os aglomerados octaédricos e 25 para os icosaédricos. Usando as leis de potência relevantes, isso dá FE =18,0 % para o octaédrico e 19,8% para os aglomerados icosaédricos. Há muito pouca diferença em FE para este tamanho do cluster, mas o cluster icosaédrico tem uma quantidade significativa de deformação devido à geminação, que pode deslocar o centro da banda d, afetando assim os resultados de ORR [40]. No entanto, dados os dados dependentes do tamanho de [38], pode ser sugerido que clusters menores produziriam dados de ORR ainda maiores. Na verdade, 4 nm Pt ₃ Os octaedros de níquel, quando dopados com Mo, produziram resultados de ORR recorde [41].

Conclusões

Estudamos 19 tipos de nanoclusters e algumas fórmulas mágicas relevantes para o número de átomos, ligações, números de coordenação e índices topológicos. Isso inclui o fcc, bcc, hcp, os sólidos platônicos, cúbico de diamante, cúbico simples e aglomerados decaédricos. A maioria desses resultados é mais detalhada do que determinado anteriormente, e um grande número é enumerado pela primeira vez. Um grande objetivo da pesquisa relacionada a materiais é a correlação da estrutura com as propriedades. Este estudo detalhado das relações mágicas para nanoclusters é um passo nessa direção. Um exemplo é a discussão da dispersão de átomos de superfície e sua relação com a atividade catalítica. É nossa intenção que esses resultados ajudem os cientistas em seus estudos da estrutura de nanoaglomerados e as propriedades associadas.

Abreviações

bcc:

cúbico centrado no corpo

cif:

arquivo de informação cristalográfica

fcc:

cúbico centrado na face

FE:

Fração exposta, dispersão

hcp:

hexagonal fechado embalado

ORR:

Reação de redução de oxidação

rW (G):

Índice reverso de Wiener

Sz (G):

Índice de Szeged

W (G):

Índice de Wiener

WW (G):

Índice Hyper-Wiener

Nanofolhas porosas de ZnO com modificação de superfície parcial para separação de cargas aprimorada e alta atividade fotocatalítica sob irradiação solar Efeitos da estrutura de contato tipo p em malha no efeito de extração de luz para diodos emissores de luz ultravioleta ultravioleta profunda Flip-Chip