Compreendendo as fórmulas de treinamento e retropropagação para perceptrons multicamadas

Este artigo apresenta as equações que usamos ao realizar cálculos de atualização de peso e também discutiremos o conceito de retropropagação.

Bem-vindo à série da AAC sobre aprendizado de máquina.

Acompanhe a série até agora aqui:

1. Como realizar a classificação usando uma rede neural:o que é o Perceptron?
2. Como usar um exemplo de rede neural simples Perceptron para classificar dados
3. Como treinar uma rede neural Perceptron básica
4. Compreendendo o treinamento de rede neural simples
5. Uma introdução à teoria de treinamento para redes neurais
6. Compreendendo a taxa de aprendizagem em redes neurais
7. Aprendizado de máquina avançado com o Multilayer Perceptron
8. A função de ativação sigmóide:ativação em redes neurais multicamadas Perceptron
9. Como treinar uma rede neural multicamadas Perceptron
10. Noções básicas sobre fórmulas de treinamento e retropropagação para percepções multicamadas
11. Arquitetura de rede neural para uma implementação Python
12. Como criar uma rede neural multicamadas Perceptron em Python
13. Processamento de sinais usando redes neurais:validação no projeto de redes neurais
14. Conjuntos de dados de treinamento para redes neurais:como treinar e validar uma rede neural Python

Chegamos ao ponto em que precisamos considerar cuidadosamente um tópico fundamental dentro da teoria das redes neurais:o procedimento computacional que nos permite ajustar os pesos de um Perceptron multicamadas (MLP) para que possa classificar com precisão as amostras de entrada. Isso nos levará ao conceito de “retropropagação”, que é um aspecto essencial do projeto de rede neural.

Atualizando pesos

As informações em torno do treinamento para MLPs são complicadas. Para piorar as coisas, os recursos online usam terminologias e símbolos diferentes e até parecem apresentar resultados diferentes. No entanto, não tenho certeza se os resultados são realmente diferentes ou apenas apresentam as mesmas informações de maneiras diferentes.

As equações contidas neste artigo são baseadas nas derivações e explicações fornecidas pelo Dr. Dustin Stansbury nesta postagem do blog. Seu tratamento é o melhor que encontrei, e é um ótimo lugar para começar se você quiser se aprofundar nos detalhes matemáticos e conceituais da descida gradiente e retropropagação.

O diagrama a seguir representa a arquitetura que implementaremos no software, e as equações abaixo correspondem a essa arquitetura, que é discutida mais detalhadamente no próximo artigo.

Terminologia

Este tópico rapidamente se torna incontrolável se não mantivermos uma terminologia clara. Usarei os seguintes termos:

• Pré-ativação (abreviado como \ (S_ {preA} \) ):Isso se refere ao sinal (na verdade, apenas um número dentro do contexto de uma iteração de treinamento) que serve como entrada para a função de ativação de um nó. É calculado por meio de um produto escalar de uma matriz contendo pesos e uma matriz contendo os valores originados de nós na camada anterior. O produto escalar é equivalente a realizar uma multiplicação elemento a elemento das duas matrizes e, em seguida, somar os elementos na matriz resultante dessa multiplicação.
• Pós-ativação (abreviado como \ (S_ {postA} \) ):Refere-se ao sinal (novamente, apenas um número no contexto de uma iteração individual) que sai de um nó. É produzido aplicando a função de ativação ao sinal de pré-ativação. Meu termo preferido para a função de ativação, denotado por \ (f_ {A} () \) , é logístico em vez de sigmóide.
• No código Python, você verá matrizes de peso marcadas com ItoH e HtoO . Eu uso esses identificadores porque é ambíguo dizer algo como "pesos da camada oculta" - seriam esses os pesos aplicados antes a camada oculta ou depois a camada oculta? Em meu esquema, ItoH especifica os pesos que são aplicados aos valores transferidos dos nós de entrada para os nós ocultos, e HtoO especifica os pesos que são aplicados aos valores transferidos dos nós ocultos para o nó de saída.
• O valor correto de saída para uma amostra de treinamento é conhecido como alvo e é denotado por T .
• Taxa de aprendizagem é abreviado como LR .
• Erro final é a diferença entre o sinal de pós-ativação do nó de saída ( \ (S_ {postA, O} \) ) e o alvo, calculado como \ (FE =S_ {postA, O} - T \) .
• Sinal de erro ( \ (S_ {ERROR} \) ) é o erro final propagado de volta para a camada oculta por meio da função de ativação do nó de saída.
• Gradiente representa a contribuição de um determinado peso para o sinal de erro. Modificamos os pesos subtraindo esta contribuição (multiplicada pela taxa de aprendizagem, se necessário).

O diagrama a seguir situa alguns desses termos dentro da configuração visualizada da rede. Eu sei - parece uma bagunça multicolorida. Peço desculpas. É um diagrama denso de informações e, embora possa ser um pouco ofensivo à primeira vista, se você estudá-lo cuidadosamente, acho que irá considerá-lo muito útil.

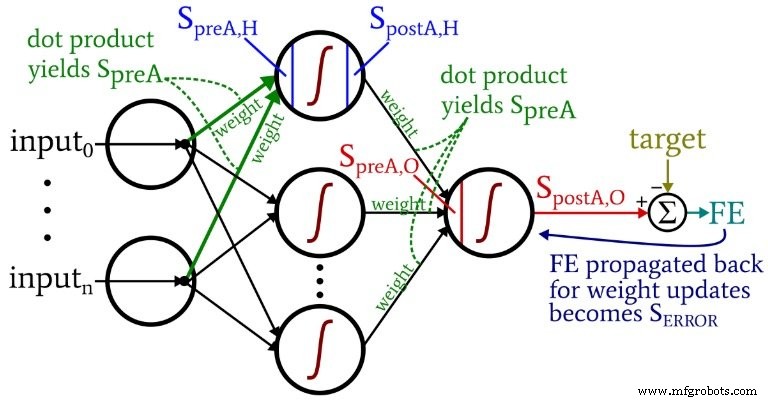
As equações de atualização de peso são derivadas tomando a derivada parcial da função de erro (estamos usando o erro quadrático somado, consulte a Parte 8 da série, que trata das funções de ativação) com relação ao peso a ser modificado. Por favor, consulte a postagem do Dr. Stansbury se você quiser ver a matemática; neste artigo, pularemos direto para os resultados. Para os pesos ocultos para a saída, temos o seguinte:

\ [S_ {ERROR} =FE \ vezes {f_A} '(S_ {preA, O}) \]

\ [gradiente_ {HtoO} =S_ {ERROR} \ vezes S_ {postA, H} \]

\ [peso_ {HtoO} =peso_ {HtoO} - (LR \ vezes gradiente_ {HtoO}) \]



Calculamos o sinal de erro l multiplicando o erro final pelo valor que é produzido quando aplicamos a derivada da função de ativação para o sinal de pré-ativação entregue ao nó de saída (observe o símbolo primo, que indica a primeira derivada, em \ ({f_A} '(S_ {preA, O}) \)). O gradiente é então calculado multiplicando o sinal de erro pelo sinal de pós-ativação da camada oculta. Por fim, atualizamos o peso subtraindo este gradiente do valor de peso atual, e podemos multiplicar o gradiente pela taxa de aprendizagem se quisermos alterar o tamanho do passo.

Para os pesos de entrada para ocultos, temos o seguinte:

\ [gradiente_ {ItoH} =FE \ times {f_A} '(S_ {preA, O}) \ times weight_ {HtoO} \ times {f_A}' (S_ {preA , H}) \ times input \]

\ [\ Rightarrow gradiente_ {ItoH} =S_ {ERROR} \ times weight_ {HtoO} \ times {f_A} '(S_ {preA, H}) \ times input \]

\ [peso_ {ItoH} =peso_ {ItoH} - (LR \ vezes gradiente_ {ItoH}) \]


Com os pesos de entrada para ocultos, o erro deve ser propagado de volta por uma camada adicional, e fazemos isso multiplicando o sinal de erro pelo peso oculto para saída conectado ao nó oculto de interesse. Portanto, se estivermos atualizando um peso de entrada para oculto que leva ao primeiro nó oculto, multiplicamos o sinal de erro pelo peso que conecta o primeiro nó oculto ao nó de saída. Em seguida, completamos o cálculo executando multiplicações análogas às das atualizações de peso oculto para a saída:aplicamos a derivada da função de ativação ao sinal de pré-ativação do nó oculto , e o valor de “entrada” pode ser considerado o sinal de pós-ativação do nó de entrada.

Retropropagação

A explicação acima já tocou no conceito de retropropagação. Quero apenas reforçar brevemente esse conceito e também garantir que você tenha familiaridade explícita com esse termo, que aparece com frequência em discussões sobre redes neurais.

A retropropagação nos permite superar o dilema do nó oculto discutido na Parte 8. Precisamos atualizar os pesos de entrada para ocultos com base na diferença entre a saída gerada da rede e os valores de saída de destino fornecidos pelos dados de treinamento, mas esses pesos influenciam a saída gerada indiretamente.

A retropropagação se refere à técnica pela qual enviamos um sinal de erro de volta para uma ou mais camadas ocultas e escalamos esse sinal de erro usando os pesos emergentes de um nó oculto e a derivada da função de ativação do nó oculto. O procedimento geral serve como uma forma de atualizar um peso com base na contribuição do peso para o erro de saída, mesmo que essa contribuição seja obscurecida pela relação indireta entre um peso de entrada para oculto e o valor de saída gerado.

Conclusão

Cobrimos muito material importante. Acho que temos algumas informações realmente valiosas sobre o treinamento de redes neurais neste artigo e espero que você concorde. A série vai começar a ficar ainda mais empolgante, então volte para ver as novas parcelas.