Um Somador Binário

Suponha que quiséssemos construir um dispositivo que pudesse adicionar dois bits binários. Esse dispositivo é conhecido como meio-somador, e seu circuito de porta é parecido com este:





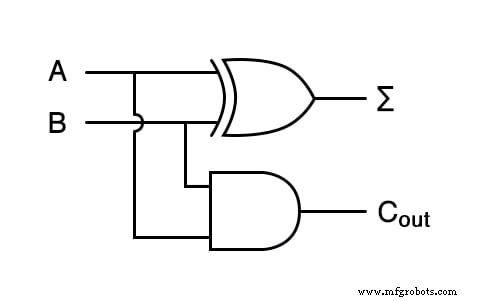
O símbolo Σ representa a "soma" de saída do meio somador, o bit menos significativo da soma (LSB). C _out representa a saída de "transporte" do meio somador, o bit mais significativo da soma (MSB).



Se implementássemos esta mesma função na lógica ladder (relé), seria assim:





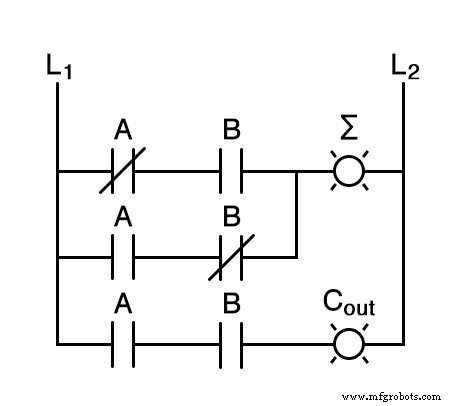
Qualquer um dos circuitos é capaz de adicionar dois dígitos binários. As “regras” matemáticas de como adicionar bits são intrínsecas à lógica cabeada dos circuitos.

Se quiséssemos realizar uma operação aritmética diferente com bits binários, como a multiplicação, teríamos que construir outro circuito. Os projetos de circuito acima irão executar apenas uma função:adicionar dois bits binários juntos. Para fazê-los fazer outra coisa, seria necessária uma nova fiação e, talvez, componentes diferentes.



Nesse sentido, os circuitos aritméticos digitais não são muito diferentes dos circuitos aritméticos analógicos (amplificador operacional):eles fazem exatamente o que foram programados para fazer, nem mais nem menos. Não estamos, entretanto, restritos a projetar circuitos digitais de computador dessa maneira.

É possível incorporar as “regras” matemáticas para qualquer operação aritmética na forma de dados digitais, em vez de conexões cabeadas entre portas. O resultado é uma flexibilidade de operação incomparável, dando origem a um tipo totalmente novo de dispositivo digital:o computador programável .

Embora este capítulo não seja de forma alguma exaustivo, ele fornece o que acredito ser uma visão única e interessante da natureza dos dispositivos programáveis ​​de computador, começando com dois dispositivos frequentemente esquecidos em livros didáticos introdutórios: memórias de tabelas de pesquisa e máquinas de estado finito .



PLANILHA RELACIONADA:

• Planilha de circuitos matemáticos binários