MATLAB - Transformações

O MATLAB fornece comando para trabalhar com transformações, como as transformações de Laplace e Fourier. As transformações são usadas na ciência e na engenharia como uma ferramenta para simplificar a análise e analisar os dados de outro ângulo.

Por exemplo, a transformada de Fourier nos permite converter um sinal representado em função do tempo em função da frequência. A transformada de Laplace nos permite converter uma equação diferencial em uma equação algébrica.

MATLAB fornece o laplace , fourier e fft comandos para trabalhar com transformações de Laplace, Fourier e Fast Fourier.

A Transformada de Laplace

A transformada de Laplace de uma função do tempo f(t) é dada pela seguinte integral −

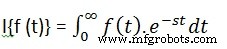
A transformada de Laplace também é denotada como transformada de f(t) para F(s). Você pode ver que esse processo de transformação ou integração converte f(t), uma função da variável simbólica t, em outra função F(s), com outra variável s.

A transformada de Laplace transforma equações diferenciais em algébricas. Para calcular uma transformada de Laplace de uma função f(t), escreva −

laplace(f(t))

Exemplo

Neste exemplo, calcularemos a transformada de Laplace de algumas funções comumente usadas.

Crie um arquivo de script e digite o seguinte código -

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

A Transformada Inversa de Laplace

O MATLAB nos permite calcular a transformada inversa de Laplace usando o comando ilaplace .

Por exemplo,

ilaplace(1/s^3)

O MATLAB executará a instrução acima e exibirá o resultado −

ans =
   t^2/2

Exemplo

Crie um arquivo de script e digite o seguinte código -

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

As Transformadas de Fourier

As transformadas de Fourier comumente transformam uma função matemática do tempo, f(t), em uma nova função, às vezes denotada por ou F, cujo argumento é frequência com unidades de ciclos/s (hertz) ou radianos por segundo. A nova função é então conhecida como transformada de Fourier e/ou espectro de frequência da função f.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Quando você executa o arquivo, o MATLAB traça o seguinte gráfico -

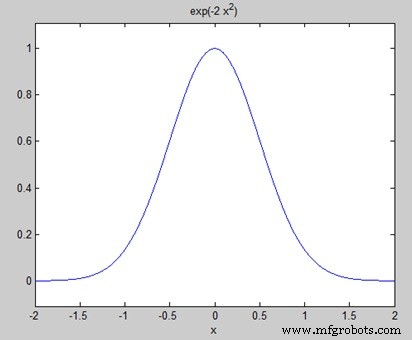
O seguinte resultado é exibido -

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

Traçando a transformada de Fourier como -

ezplot(FT)

Dá o seguinte gráfico -

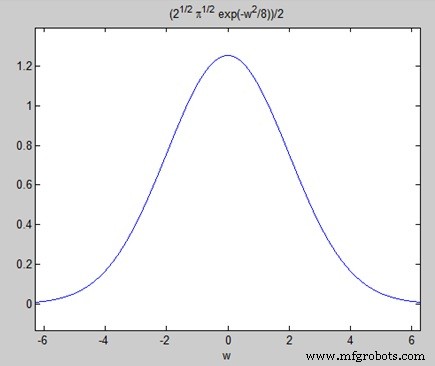
Transformadas inversas de Fourier

O MATLAB fornece o ifourier comando para calcular a transformada inversa de Fourier de uma função. Por exemplo,

f = ifourier(-2*exp(-abs(w)))

O MATLAB executará a instrução acima e exibirá o resultado −

f =
   -2/(pi*(x^2 + 1))