Um Projeto Eficiente e Eficaz de Nanofios InP para Captação Máxima de Energia Solar

Resumo

As células solares baseadas em matrizes de nanofios semicondutores (NW) com dimensões de sub-comprimento de onda prometem um desempenho comparável ou melhor do que suas contrapartes planas, aproveitando as vantagens do forte acoplamento e captura de luz. Neste artigo, apresentamos um projeto analítico preciso e de economia de tempo para parâmetros geométricos ideais de NWs InP alinhados verticalmente para absorção máxima de energia solar. As densidades de corrente de curto-circuito são calculadas para cada matriz NW com diferentes dimensões geométricas sob iluminação solar. As dimensões geométricas ideais são apresentadas quantitativamente para diâmetros simples, duplos e múltiplos das matrizes NW dispostas quadradas e hexagonais, alcançando a densidade máxima de corrente de curto-circuito de 33,13 mA / cm ² . Ao mesmo tempo, simulações numéricas intensivas no domínio do tempo de diferenças finitas são realizadas para investigar os mesmos arranjos NW para a maior absorção de luz. Em comparação com simulações demoradas e resultados experimentais, as densidades máximas de corrente de curto-circuito previstas têm tolerâncias abaixo de 2,2% para todos os casos. Esses resultados demonstram inequivocamente que este método analítico fornece uma rota rápida e precisa para orientar o projeto de células solares com base em InP NW de alto desempenho.

Histórico

Para células solares de geração futura, matrizes de nanofios semicondutores (NW) revelaram um novo caminho para reduzir significativamente o consumo de material e o custo de fabricação, mantendo ou mesmo melhorando o desempenho do dispositivo em comparação com sua película fina ou homólogos a granel [1, 2]. Esta fascinante característica é amplamente atribuída às notáveis ​​propriedades ópticas dos NWs, incluindo aumento da absorção [3, 4] e seletividade espectral [5,6,7]. Entre os vários materiais III-V, os arranjos InP NW têm atraído intensos esforços de pesquisa para aplicação em células solares devido ao bandgap direto e à baixa velocidade de recombinação de superfície intrínseca [8]. Até o momento, a maior eficiência de conversão de energia atingiu 13,8% para matrizes InP NW em uma célula de 1 mm ² na área [9].

Uma vez que as propriedades ópticas das matrizes NW podem ser ajustadas distintamente pelo ajuste de sua geometria tridimensional, para melhorar ainda mais o desempenho das células solares baseadas em NW, grande atenção foi colocada em como otimizar a morfologia e topologia das matrizes III-V NW para maximizar a absorção de luz [5, 9,10,11,12,13]. Especificamente, o diâmetro, a periodicidade e o arranjo dos NWs foram investigados para maximizar a absorção de energia solar [6, 14,15,16]. É relatado que o ajuste do diâmetro do NW mudará os modos ópticos existentes no NW. Isso levará a máximos de absorção de luz localizada para os comprimentos de onda incidentes correspondentes aos respectivos modos ressonantes [5, 6, 17, 18]. Além disso, matrizes NW com periodicidade otimizada ou taxa de preenchimento (FR) podem suprimir a reflexão e a transmissão enquanto aumentam o espalhamento para a luz incidente, resultando no caminho óptico prolongado e, portanto, na absorção de luz aprimorada [19,20,21]. Além disso, Martin Foldyna et al. concluíram que a dependência da absorção de luz no arranjo dos arranjos NW é bastante pequena, uma vez que o efeito de captura de luz dos NWs é baseado no guia de ondas individual quando o acoplamento de luz entre os NWs vizinhos é desprezado [22].

Para encontrar a colheita máxima de energia solar, o efeito dos parâmetros tridimensionais e o arranjo das matrizes NW devem ser considerados juntos. No entanto, a maioria das dimensões geométricas ótimas relatadas e arranjo de matrizes NW para a colheita máxima do espectro solar são ainda ótimos locais determinados pelo espaço de parâmetros. Além disso, a combinação do espectro solar incidente com as propriedades dispersivas do material adiciona mais dificuldade para resolver analiticamente este problema. Portanto, simulações numéricas intensas e demoradas, como o domínio de tempo de diferenças finitas (FDTD), são frequentemente adotadas para resolver esse problema de otimização de multiparâmetros. Sturmberg et al. relataram um método semi-analítico para estreitar a faixa das dimensões ótimas de arranjos NW de diâmetro único [13]. Embora este método seja aplicável a vários materiais, as simulações de FDTD ainda devem ser acompanhadas para encontrar os valores ideais exatos. Além disso, este método é menos útil para um absorvedor excelente combinado com matrizes NW multi-raios [23].

Neste artigo, apresentamos um projeto analítico para dimensões geométricas ideais de matrizes InP NW de diâmetro único, duplo e múltiplo para maximizar a absorção de energia solar. Os diâmetros de NWs são determinados pela ressonância do modo de vazamento e pela teoria de Mie, enquanto as periodicidades são identificadas pela construção de uma camada média efetiva para minimizar a reflexão e a transmissão da luz. Ambas as matrizes NW com distribuição quadrada e hexagonal são consideradas. Além disso, simulações intensivas de FDTD são acompanhadas para verificar a eficácia do nosso método. O bom casamento das maiores densidades de corrente de curto-circuito geradas a partir dos arranjos NW com os parâmetros geométricos calculados e os valores obtidos nas simulações FDTD comprovam a eficácia do método proposto para guiar o projeto prático de células fotovoltaicas baseadas em NW.

Projeto para extração máxima de luz de PNs InP

Matrizes InP NW alinhadas verticalmente são colocadas sobre um SiO semi-infinito ₂ substrato como esquematicamente mostrado na Fig. 1 com disposição quadrada ou hexagonal. Células unitárias repetíveis na Fig. 1a, b inserções explicam as respectivas dimensões de caracterização para cada arranjo. Esta morfologia e topologia dos arranjos NW estão de acordo com a maioria das estruturas de células solares baseadas no InP NW [11, 12, 23, 24]. Dentro de cada uma das células unitárias, os NWs têm diâmetros iguais ou diferentes que D _i . Periodicidade p é definido como a distância de centro a centro de um par de NWs adjacentes que tem o mesmo valor para NWs dispostos de forma quadrada, enquanto valores diferentes para arranjos NW hexagonais. Consequentemente, o FR das matrizes NW quadradas é definido como \ (\ pi {\ sum} _ {\ mathrm {i} =1} ^ 4 {D_i} ^ 2 / {(4p)} ^ 2 \) tendo o valor máximo de π / 4 quando os NWs ocupam a maior porcentagem de volume da célula unitária [25]. Da mesma forma, o FR para matrizes hexagonais NW é definido como \ (\ pi {\ sum} _ {\ mathrm {i} =1} ^ 2 {D_i} ^ 2 / \ left (4 \ sqrt {3} {p} ^ 2 \ right) \) com o valor máximo de \ (\ pi \ sqrt {3} / 6 \) [22]. O comprimento l do NW é definido como 2 μm para todos os casos, uma vez que são longos o suficiente para absorver mais de 90% da energia incidente com projeto adequado [26].

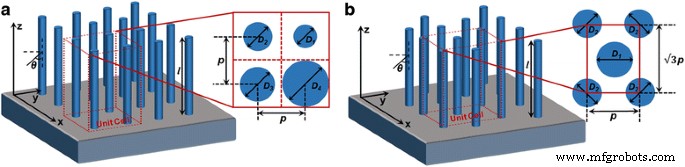
Esquemas de matrizes InP NW alinhadas verticalmente. a Squarely e b matrizes hexagonais NW com inserções explicando suas respectivas células unitárias

A fim de determinar analiticamente cada parâmetro geométrico de matrizes NW, o problema de otimização de múltiplos parâmetros para a colheita máxima de luz é decomposto em dois processos:(1) controle do modo ressonante determinante do diâmetro NWs e (2) refletância e transmitância mínimas afetadas por FR de energia solar incidente. Nós construímos a relação do parâmetro geométrico individual com o respectivo processo determinante e identificamos cada valor ótimo que leva à absorção máxima de luz. Matrizes de diâmetro duplo NW são escolhidas como o exemplo de projeto para ilustração do método proposto. Dimensões geométricas ideais de matrizes de diâmetro único NW como um caso mais simples também podem ser adquiridas durante a derivação. O diâmetro e a periodicidade para matrizes de quatro diâmetros NW também podem ser calculados como uma extensão do exemplo. Para matrizes NW de diâmetros duplos dispostos em quadratura, os diâmetros das diagonais NW têm o mesmo valor que D _principal e os diâmetros dos restantes dois NWs são nomeados como D _suplementar . Para arranjos hexagonais NW, o diâmetro do centro NW é D _principal e os diâmetros dos NWs na periferia são D _suplementar .

É relatado que os arranjos NW podem suportar modos de ressonância guiada / vazada, cada um dos quais levando a fortes picos de absorção. Além disso, a natureza fundamental do guia de ondas sugere que o número do modo cresce com o aumento do diâmetro de NW. Consequentemente, o diâmetro ideal de NW deve ser grande o suficiente para suportar mais modos de modo a incluir um maior número de ressonâncias de absorção. No entanto, diâmetros muito grandes de NWs são menos preferíveis, uma vez que os modos de ordem superior que eles suportam possuem mais nós que se acoplam de forma menos eficiente às ondas planas incidentes [13]. Além disso, a propriedade do material e o espectro solar incidente colocam outras limitações na seleção do diâmetro ideal. Somente quando os modos ressonantes estão dentro da região de absorção, eles podem contribuir para a fotocorrente. A região de absorção é definida pela superposição da faixa de absorção do material de até comprimento de onda crítico e o espectro incidente AM 1.5G [27].

Como resultado, para determinar quantitativamente o D _principal das matrizes NW, a ressonância em modo vazado é inicialmente adotada para calcular os respectivos comprimentos de onda ressonantes para diferentes diâmetros de NWs [2]. Isso dá a distribuição dos modos ressonantes na região de absorção. Portanto, o D ideal _principal deve suportar dois modos para satisfazer todos os critérios acima. Em segundo lugar, a teoria de Mie é adotada para calcular as eficiências de absorção normalizadas desses NWs na etapa um. A rigor, a teoria de Mie não pode ser aplicada à situação em que o vetor da onda incidente se alinha perfeitamente paralelo ao eixo das NWs, uma vez que a equação dos autovalores está mal definida [28]. No entanto, esta situação pode ser aproximada como o incidente envidraçado da luz incidente (ângulo de incidência muito pequeno θ em relação ao eixo de NW) uma vez que na interface dos arranjos NW, a frente de onda da luz incidente será perturbada pelo alto índice de NWs que introduz componentes transversais ao vetor de onda permitindo a adoção da teoria de Mie [18]. Portanto, o D ideal _principal são aqueles que suportam dois modos, mantendo a largura total na metade do máximo (FWHM) do modo ressonante mais baixo no espectro de eficiência de absorção normalizado dentro da região de absorção. Após a aquisição de D _principal , o D _suplementar é calculado na condição de que os NWs devem suportar um modo para reduzir a reflexão e economia de material e seu comprimento de onda ressonante deve corresponder ao vale do D _principal Espectro de eficiência de absorção normalizado.

A periodicidade dos arranjos NW pode ser calculada pela construção de uma camada média efetiva. Esta camada artificial representa o comportamento de reflexão e transmissão dos arranjos NW que está relacionado apenas ao material FR. Como resultado, o diâmetro, a periodicidade e a disposição das matrizes NW são removidos do cálculo. Desta forma, a transmitância e refletância de matrizes NW podem ser avaliadas aplicando as equações de Fresnel nesta camada de meio efetiva e, portanto, o FR ideal pode ser analisado. Com base na relação de FR e periodicidade, as periodicidades para arranjos NW hexagonais e quadrados são obtidas. A descrição detalhada de nosso método proposto é apresentada nas seções a seguir.

A. Diâmetros ideais de matrizes InP NW para colheita de luz máxima

Para aumentar a absorção de luz, o número de modos ressonantes que levam a fortes picos de absorção deve ser maximizado dentro da região de absorção. Na extremidade azul da região de absorção, o espectro incidente AM 1.5G confina 300 nm como a região de alta energia. O comprimento de onda crítico λ _c de 925 nm (bandgap de InP 1,34 eV) limita a extremidade vermelha da região de absorção. Como resultado, fica provado que os InP NWs que suportam dois modos ressonantes localizados dentro da região absorvente são capazes de melhor melhorar a absorção de luz [29]. Expandimos essa conclusão e usamos a teoria de Mie para calcular o valor exato.

De acordo com a conclusão acima, o intervalo de D _principal pode ser calculado a partir da equação do valor próprio derivada das equações de Maxwell [18]. Considerando a distribuição de campo anti-simétrica no plano das ondas do plano incidente, apenas o HE _1m os modos podem ser efetivamente estimulados para contribuir com a absorção de NWs verticalmente alinhados [5]. Estes HE _1m modos satisfazem a equação de autovalor, e os comprimentos de onda ressonantes podem ser obtidos assumindo que a parte real da constante de propagação Re (β _z ) do modo ao longo da direção axial NW se aproxima de zero, conforme mostrado na Eq. (1). k _cil e k _ar são as componentes transversais do vetor de onda dentro dos NWs e no ar enquanto ε _cil e ε _ar são as respectivas permissividades. J ₁ e H ₁ ⁽¹⁾ são as funções de Bessel e Hankel de primeira ordem do primeiro tipo. Como consequência, a faixa em que o diâmetro primário cai pode ser recebida na condição de que o HE ₁₁ correspondente e HE ₁₂ o modo encontra-se na região de absorção.
$$ \ frac {\ varepsilon _ {\ mathrm {cyl}} {J} _1 ^ {\ prime} \ left ({k} _ {\ mathrm {cyl}} {D} _ {\ mathrm {major}} / 2 \ right)} {k _ {\ mathrm {cyl}} {J} _1 \ left ({k} _ {\ mathrm {cyl}} {D} _ {\ mathrm {major}} / 2 \ right)} - ​​\ frac {\ varepsilon _ {\ mathrm {air}} {H_1 ^ {(1)}} ^ {\ prime} \ left ({k} _ {\ mathrm {air}} {D} _ {\ mathrm {major}} / 2 \ right)} {k _ {\ mathrm {air}} {H} _1 ^ {(1)} \ left ({k} _ {\ mathrm {air}} {D} _ {\ mathrm {major}} / 2 \ direita)} =0. $$ (1)
De acordo com a teoria de Mie, a eficiência de absorção Q _abs de NWs é definido pela razão entre a área de coleta de energia e o tamanho geométrico dos NWs. A expressão analítica da eficiência de absorção Q _abs é dado abaixo, e o formalismo matemático exato da teoria de Mie pode ser encontrado na referência [30]. Aqui, \ (\ overline {n} =n + ik \) é o índice de refração complexo; como mencionado acima, J _i e H _i ⁽¹⁾ são as funções de Bessel e Hankel de primeiro tipo de ordem i .
$$ {\ displaystyle \ begin {array} {c} {Q} _ {\ mathrm {abs}, \ mathrm {TM}} =\ frac {2} {x} \ operatorname {Re} \ left ({b} _0 + 2 \ sum \ limits_ {i =1} ^ {\ infty} {b} _i \ right) - \ frac {2} {x} \ left [{\ left | {b} _0 \ right |} ^ 2 +2 \ sum \ limits_ {i =1} ^ {\ infty} {\ left | {b} _i \ right |} ^ 2 \ right] \\ {} {Q} _ {\ mathrm {abs}, \ mathrm {TM}} =\ frac {2} {x} \ operatorname {Re} \ left ({a} _0 + 2 \ sum \ limits_ {i =1} ^ {\ infty} {a} _i \ right) - \ frac {2} {x} \ left [{\ left | {a} _0 \ right |} ^ 2 + 2 \ sum \ limits_ {i =1} ^ {\ infty} {\ left | {a} _i \ right |} ^ 2 \ right] \ end {array}} $$ (2) $$ {\ displaystyle \ begin {array} {c} {a} _i =\ frac {\ overrightarrow {n} {J} _i \ left (\ overrightarrow {n} x \ right) {J} _i ^ {\ prime} (x) - {J} _i \ left (\ overrightarrow {n} x \ right) {J} _i ^ {\ prime} (x )} {\ overrightarrow {n} {J} _i \ left (\ overrightarrow {n} x \ right) {H_i ^ {(1)}} ^ {\ prime} (x) - {J} _i ^ {\ prime } \ left (\ overrightarrow {n} x \ right) {H} _i ^ {(1)} (x)} \\ {} {b} _i =\ frac {J_i \ left (\ overrightarrow {n} x \ direita) {J} _i ^ {\ prime} (x) - \ overrightarrow {n} {J} _i \ left (\ overrightarrow {n} x \ right) {J} _i ^ {\ prime} (x)} { J_i \ left (\ overrightarrow {n} x \ right) {H_i ^ {(1)}} ^ {\ prime } (x) - \ overrightarrow {n} {J} _i ^ {\ prime} \ left (\ overrightarrow {n} x \ right) {H} _i ^ {(1)} (x)} \ end {array} } $$ (3)
Após a aquisição do Q _abs do HE ₁₁ modo, o FWHM do respectivo diâmetro de NWs pode ser encontrado e, portanto, o diâmetro ideal para a colheita de luz máxima é determinado. Após a decisão do diâmetro principal, o diâmetro suplementar é confirmado na condição de que seu comprimento de onda de pico de absorção normalizado deve corresponder ao vale de eficiência de absorção normalizado do diâmetro principal. Para matrizes de quatro diâmetros NW, o terceiro e o quarto diâmetros são determinados de maneira semelhante. Seus picos de eficiência de absorção normalizados devem corresponder aos vales da superposição do espectro de eficiência de absorção normalizado dos NWs primário e secundário. É digno de nota que, exceto para os NWs principais, o segundo, terceiro e quarto NWs são desejados para suportar apenas um modo, uma vez que o tamanho do diâmetro pequeno pode reduzir a refletância na interface ar-NW e reduzir o consumo de material.

B. FR ideal de matrizes InP NW para colheita de luz máxima

Vários trabalhos publicados divulgaram que com diâmetros fixos de NWs; a absorção dos NWs aumentará com o FR inicialmente e então diminuirá após um certo valor ótimo [13]. O aumento da absorção de luz é geralmente atribuído ao aumento da porcentagem de volume dos materiais semicondutores com altos coeficientes de absorção. À medida que FR aumenta ainda mais, o índice de refração médio das matrizes NW aumenta e, portanto, a reflexão aumenta, o que reduz a absorção de luz. Portanto, um limite superior no FR deve ser encontrado para otimizar a influência da reflexão e transmissão de Fresnel para maximizar a absorção dos arranjos NW. A Figura 2 ilustra esquematicamente que uma camada média eficaz de índice de refração complexo é criada para representar a refração e o comportamento de transmissão dos arranjos NW. Desta forma, as periodicidades e diâmetros dos NWs são removidos do cálculo. Consequentemente, o cálculo de Fresnel da reflexão e transmissão da camada de meio efetiva pode ser usado para refletir as propriedades dos arranjos NW. A natureza exata dentro desta camada de meio artificial não é considerada, desde que possam representar a reflexão e transmissão de matrizes NW. Derivações matemáticas detalhadas são fornecidas abaixo.

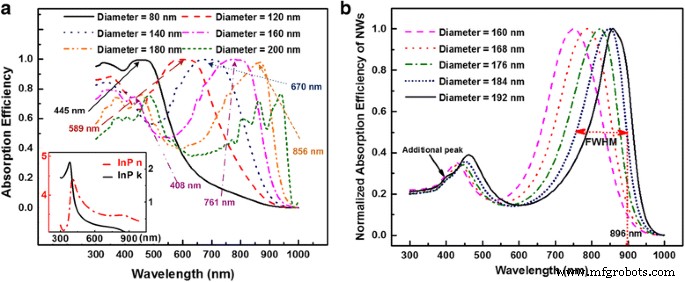
Reflexão de luz, transmissão e absorção de NWs e camada média efetiva. a Matrizes InP NW e b a camada média efetiva correspondente com a mesma espessura

A parte real do índice de refração da camada média efetiva n _{em_real} são determinados pela formulação de Bruggeman [31] na Eq. (4) onde Ɛ _em , e Ɛ _NW são a permissividade da camada média efetiva e InP, respectivamente. A parte imaginária do índice de refração n _{em_imag} é calculado pela Teoria da Média de Volume [32, 33] na Eq. (5) onde o n _{NW_real} , n _{NW_imag} , n _{air_real} e n _{air_imag} são a parte real e imaginária do índice de refração de NW e ar. O FR _opt ideal é definido como o FR tal que a absortância Abs (λ) =1 - R (λ) - T (λ) é maximizado usando as equações de Fresnel.
$$ {\ displaystyle \ begin {array} {l} \ left (1- \ mathrm {FR} \ right) \ frac {\ varepsilon _ {\ mathrm {air}} ^ 2 - {\ varejpsilon} _ {\ mathrm { em}} ^ 2} {\ varepsilon _ {\ mathrm {air}} ^ 2 + 2 {\ varejpsilon} _ {\ mathrm {em}} ^ 2} + \ mathrm {FR} \ frac {\ varepsilon _ {\ mathrm { NW}} ^ 2 - {\ varepsilon} _ {\ mathrm {em}} ^ 2} {\ varepsilon _ {\ mathrm {NW}} ^ 2 + 2 {\ varepsilon} _ {\ mathrm {em}} ^ 2} =0 \\ {} {n} _ {\ mathrm {em} \ _ \ mathrm {real}} =\ operatorname {Re} \ left (\ sqrt {\ varepsilon _ {\ mathrm {em}}} \ right) \ end {array}} $$ (4) $$ {\ displaystyle \ begin {array} {l} \ mathrm {A} =\ mathrm {FR} \ left ({n} _ {\ mathrm {NW} \ _ \ mathrm {real}} ^ 2- {n} _ {\ mathrm {NW} \ _ \ mathrm {imag}} ^ 2 \ right) + \ left (1- \ mathrm {FR} \ right) \ left ({n } _ {\ mathrm {air} \ _ \ mathrm {real}} ^ 2- {n} _ {\ mathrm {air} \ _ \ mathrm {imag}} ^ 2 \ right) \\ {} B =2 \ mathrm {FR} {n} _ {\ mathrm {NW} \ _ \ mathrm {real}} {n} _ {\ mathrm {NW} \ _ \ mathrm {imag}} + 2 \ left (1- \ mathrm { FR} \ direita) {n} _ {\ mathrm {ar} \ _ \ mathrm {real}} {n} _ {\ mathrm {ar} \ _ \ mathrm {imag}} \\ {} {n} _ { \ mathrm {em} \ _ \ mathrm {imag}} =\ sqrt {\ frac {-A + \ sqrt {A ^ 2 + {B} ^ 2}} {2}} \ end {array}} $$ (5 )
Ao substituir as matrizes NW por uma película fina de espessura igual, a refletância R (λ) e T (λ) transmitância de matrizes NW pode ser estimada usando as equações de Fresnel. Os primeiros dois termos da série infinita de reflexão e transmissão de Fabry-Perot estão incluídos na Fig. 2b. Derivações matemáticas detalhadas também podem ser encontradas nas informações de apoio da referência [13]. Nesse estágio, os diâmetros ideais e o FR são determinados e a periodicidade correspondente pode ser adquirida com base na definição do FR. Com as dimensões geométricas ideais, os arranjos NW devem levar à absorção máxima de luz. Densidade de corrente de curto-circuito J _sc é usado principalmente para medir a capacidade de coleta de luz, assumindo que cada fóton absorvido leva a uma separação de excitons seguida por uma coleção de portadores bem-sucedida. A definição é mostrada na Eq. (6) onde A (λ) é a absorção dentro dos nanofios em função do comprimento de onda incidente, e N (λ) é o número de fótons por unidade de área por segundo para o comprimento de onda incidente do espectro solar padrão.
$$ {J} _ {\ mathrm {sc}} =q \ underset {\ mathrm {AM} 1,5 \ mathrm {G}} {\ int} A \ left (\ lambda \ right) N \ left (\ lambda \ direita) d \ lambda $$ (6)

Resultados e discussão

Diâmetros simples e múltiplos de arranjos InP NW de arranjos quadrados e hexagonais demonstram a validade do método proposto. Enquanto isso, simulações numéricas de FDTD (Lumerical FDTD Solutions 8.15) também são fornecidas para comparação com nosso método. A condição de limite periódica é aplicada ao longo de x e y eixos enquanto a condição de correspondência perfeita é definida ao longo de z eixo conforme ilustrado na Fig. 1. Os InP NWs estão verticalmente posicionados em SiO ₂ substrato. As constantes ópticas para InP e SiO ₂ são de dados de materiais da Palik fornecidos por Lumerical. O espaço de parâmetro para diâmetros de NWs varia de 50 a 200 nm, enquanto o FR é de 0,05 aos valores máximos possíveis para NWs quadrados e hexagonais.

A. Coleta máxima de luz para diâmetro único InP NWs

A Figura 3a mostra a eficiência de absorção de luz para matrizes de diâmetro único InP NW quando FR é 0,05 com as constantes ópticas fornecidas na inserção. Os respectivos comprimentos de onda ressonantes são calculados e marcados nos picos de absorção correspondentes que correspondem bem aos resultados da simulação FDTD. O desvio para o vermelho de HE ₁₁ o modo ressonante pode ser facilmente observado com o aumento do diâmetro dos NWs. Além disso, o cálculo e a simulação provam que o modo ressonante evolui de um para dois modos no diâmetro de 140 nm. Portanto, o valor ideal para absorção máxima de luz deve ser maior do que 140 nm e menor do que 200 nm, onde dois modos são excitados dentro de cada NW. Para encontrar o valor ideal de diâmetro, a eficiência de absorção normalizada de matrizes NW é fornecida na Fig. 3b mostrando as matrizes NW que suportam dois modos e ainda mantêm o FWHM dentro da região de absorção. Portanto, o maior valor de 184 nm de diâmetro é escolhido como o diâmetro ideal sem qualquer pico adicional. Curiosamente, o projeto de célula solar InP NW de maior eficiência de conversão de energia atualizado adotou o diâmetro ideal de 180 nm. Seus diâmetros de NWs foram experimentalmente otimizados variando de 50 a 300 nm com 10 nm como a etapa de aumento [9]. Comparado com nossa previsão de 184 nm, uma tolerância estreita de 4 nm demonstra a precisão de nosso método.

Eficiência de absorção dependente do comprimento de onda de InP NWs e eficiência de absorção normalizada. a Eficiência de absorção de NWs com detalhe explicando as constantes ópticas. b Eficiência de absorção calculada pela teoria de Mie

A proporção de enchimento é obtida analiticamente usando camada de meio eficaz na seção B do método descrito. A eficiência de absorção de luz da camada efetiva da mesma altura que os arranjos InP NW é mostrada na Fig. 4. Em geral, a capacidade de captação de luz aumenta inicialmente, atinge seu valor máximo e diminui gradualmente conforme o FR se aproxima de um valor maior. Esta tendência é atribuída à mudança da luz transmitida e refletida conforme os índices de refração complexos mudam devido à variação de FR. Especificamente, quando FR aumenta de 0,05 para 0,2, devido à adição de material InP, mais luz é absorvida antes de ser transmitida para fora dos arranjos NW. No entanto, essa tendência aumenta até que FR atinge 0,2, e aumento adicional de FR causa alto índice de refração complexo da camada equivalente que leva à impedância óptica entre os arranjos de ar e NW. Como resultado, a refletância na superfície incidente aumenta rapidamente, o que diminui a absorção de luz [13]. Portanto, o valor ideal para FR é 0,2 e as periodicidades para arranjos NW quadrados e hexagonais são 364,63 e 391,82 nm, respectivamente.

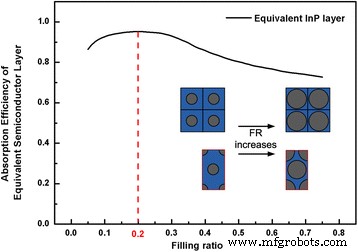
Eficiência de absorção de camada média efetiva para matrizes InP NW em função de FR

As densidades de corrente de curto-circuito para várias combinações de diâmetros e FRs são mostradas na Fig. 5. Isso demonstra claramente que o arranjo de NWs tem pouco efeito na maior absorção de luz. Além disso, independentemente dos arranjos das matrizes NW, nosso método pode ser aplicado e obter resultados precisos. O máximo J _sc com dimensões geométricas ideais calculadas para arranjos InP NW são calculados para arranjo quadrado e hexagonal, respectivamente. O máximo analítico predito J _sc é 32,11 e 32,06 mA / cm ² para matrizes NW quadradas e hexagonais levando a tolerância de 0,33 e 0,1%, respectivamente, em comparação com os resultados da simulação FDTD.

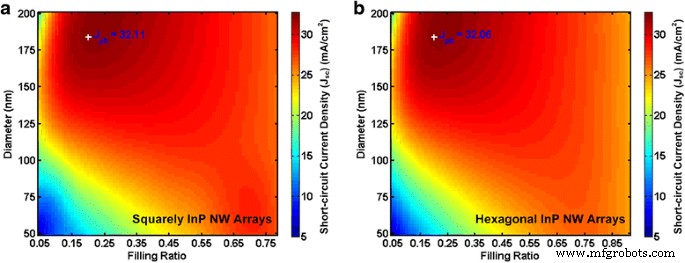
Valores máximos previstos teóricos em comparação com simulações de FDTD. a Squarely e b matrizes hexagonais de diâmetro único InP NW

B. Coleta máxima de luz para diâmetro duplo InP NWs

Adicionar um diâmetro secundário aos arranjos NW foi investigado por vários grupos para aumentar ainda mais a captação de energia solar [22, 29] por simulações demoradas [34]. A partir da discussão acima, nosso método fornece uma maneira de abordar rapidamente os diâmetros NWs necessários. O comprimento de onda ressonante dos NWs suplementares deve corresponder ao vale de absorção do diâmetro principal dos NWs, que é 585 nm, conforme mostrado na Fig. 3b. Além disso, os NWs devem suportar apenas um modo ressonante. Essas duas conclusões levam a D _suplementar de 119 nm. O FR ideal de 0,2 ainda é verdadeiro nas matrizes de diâmetro duplo InP NW, e a periodicidade é calculada como 307 e 329,95 nm para o arranjo quadrado e hexagonal das matrizes NW. A Figura 6 fornece uma visão geral da variação das densidades de corrente de curto-circuito em função de D _principal , D _suplementar e FR para dois tipos de matrizes NW. Geralmente, a colheita de luz aumenta com FR, atinge seu valor máximo e cai. Quando FR é 0,2, as inserções na Fig. 6 exibem o J mais alto _sc de 32,96 e 32,95 mA / cm ² para NWs de InP quadrados e hexagonais. Comparado com os valores máximos de simulações como 33,34 e 33,26 mA / cm ² , as tolerâncias são 1,1 e 0,9% para NWs quadrados e hexagonais. A Figura 6 também mostra que à medida que FR cresce, o acoplamento entre NWs vizinhos não pode ser negligenciado. A energia pode ser transferida para os NWs vizinhos que suportam o mesmo modo de vazamento, causando a competição da energia incidente [35], que é prejudicial à absorção geral da luz. Quando o FR é o mesmo para ambos os arranjos, p _quadrado ² / p _hexagonal ² é \ (\ sqrt {3} / 2 \). Portanto, o p _hexagonal é 1,08 vezes do p _quadrado que tem menos acoplamento de modo entre NWs do que matrizes quadradas. Isso explica as diferenças da coleta de luz das duas matrizes quando FR é 0,05 e 0,4.

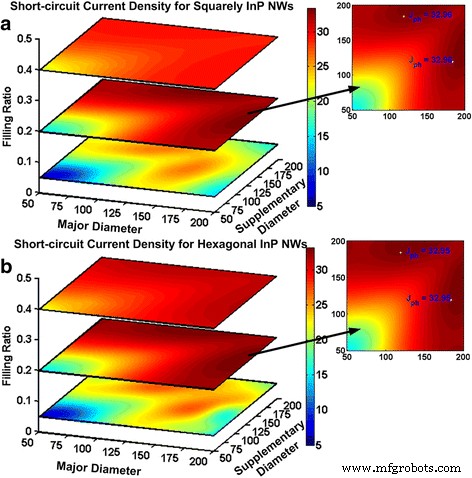
Densidades de corrente de curto-circuito em função dos diâmetros principais suplementares e FRs. a Squarely e b matrizes hexagonais InP NW onde as inserções mostram diâmetros ideais para os respectivos arranjos NW

C. Coleta máxima de luz para quatro diâmetros InP NWs

Múltiplos diâmetros de matrizes NW também atraem muito interesse de pesquisa para alcançar absorção próxima da unidade em toda a região de absorção [29]. No entanto, apenas um número limitado de combinações de diâmetro é fornecido, uma vez que a aquisição de dados de massa requer uma grande quantidade de tempo. Esse problema pode ser resolvido em nosso método de projeto analítico, e quatro diâmetros de matrizes InP NW dispostas em quadratura são fornecidos como exemplo. O tempo total gasto para concluir todos os cálculos usando nosso método é igual ao tempo gasto por apenas uma simulação FDTD usando o mesmo computador pessoal. Após a aquisição dos diâmetros principal e suplementar dos NWs, o terceiro e o quarto diâmetros dos NWs podem ser calculados de maneira semelhante. A superposição da eficiência de absorção normalizada do diâmetro principal e suplementar de NWs é mostrada na Fig. 7 com vales de absorção localizados em 486 e 704 nm. Portanto, o terceiro e o quarto diâmetro de NWs podem ser calculados para satisfazer as condições de que cada um deles suporta apenas um modo, e os comprimentos de onda ressonantes correspondem aos dois vales de absorção na Fig. 7. Consequentemente, o terceiro e o quarto diâmetros para matrizes InP NW são obtidos como 92 e 148 nm. Com o FR ótimo de 0,2, cuja validade é independente do arranjo de NW e diâmetros, a periodicidade pode ser obtida como 277,41 nm para matrizes InP NW.

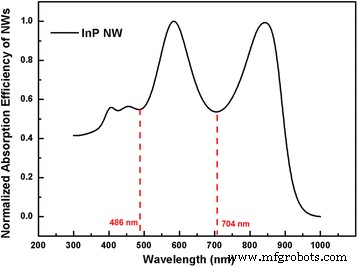
Superposição das eficiências de absorção dos diâmetros principais e suplementares dos NWs do InP

The light absorption spectrum for the optimal combination of four NWs is provided in Fig. 8 from which the near-unity light absorption is achieved by the well selection of individual NWs. FDTD simulation results with four diameters’ combinations for squarely arranged NW arrays are shown in Fig. 9. To gain an overview of this multi-parameter optimization problem, two sets of coordinates are employed. The inner x e y axes denote the major and supplementary diameters whereas the outer x e y axes represent the third and fourth diameters. Due to the huge number of combinations of diameters, limited third and fourth diameters are deliberately selected to represent the whole absorption trend. From Fig. 3, the 80 nm is chosen as single mode resonance within NWs; 140 nm reflects the evolvement from single to double modes existence in NWs; 170 nm indicates the upper end of double modes existence while remain FWHM lying within absorbing region. Each intersect of the dash lines indicates different combination of the third and fourth diameters whereas the major and supplementary diameter run through 50 to 200 nm. When the diameters have larger values than 140 nm in Fig. 9, the majority of combinations of diameters will lead to the J _sc above 30 mA/cm ² . When all of the diameters reach above 170 nm, the average of J _sc can be 32 mA/cm ² . These results are also reflected in Figs. 5a and 6a. Compared with single or double diameter NW arrays, optimized four diameter NW arrays indeed lead to higher J _sc . The highest J _sc for four diameters InP NW arrays with our calculated geometrical dimensions is 33.13 mA/cm ² with a tolerance of 2.2%.

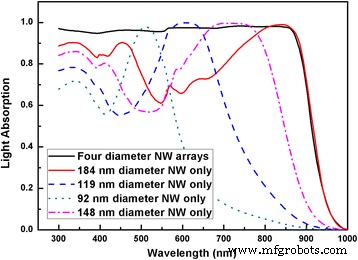
Light absorption of four diameter InP NW arrays

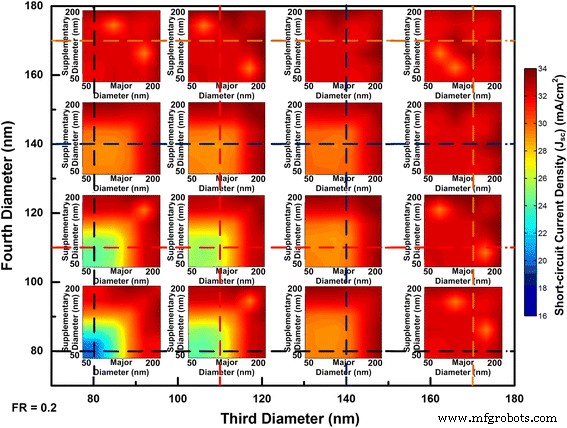
Short-circuit current densities change with the major, supplementary, third, and fourth InP NWs

Conclusões

In this study, we present model for effective and fast design of both squarely and hexagonal InP NW arrays to achieve the highest light harvesting for photovoltaic application. Geometrical dimensions for vertically aligned single, double, and multiple diameters of NW arrays are investigated. Compared with time-consuming FDTD simulations, our predicted maximal short-circuit current densities with calculated three-dimensional NW arrays remain tolerances below 2.2% for all cases. For single diameter NW arrays, the optimal diameter is 184 nm which is only 4 nm difference to the reported highest efficiency InP NW solar cells. In the multiple diameter NW arrays, the diameters of the rest of NWs are optimized to satisfy the conditions that they support only one resonant mode and the corresponding wavelengths match the absorption valley of the major NWs. Moreover, the FR of the NW array is optimized to be 0.2 by creating an effective medium layer which is regardless of the diameter, periodicity, and arrangements of NWs. Compared with the optical modeling, the predicted highest short-circuit current densities for single diameter NW arrays lie within 0.33 and 0.1% tolerance for squarely and hexagonal NW array. The arrangements of NW array have little influence on the light absorption with optimal geometrical parameters, but the coupling among neighboring NWs becomes serious for multiple diameter NWs at large FR value. Squarely arranged four diameter NW arrays were also presented and the highest short-circuit current densities predicted to be 33.13 mA/cm ² with a low tolerance of 2.2%. The time-efficient, high precision with wide suitability of the proposed design for InP NW arrays demonstrate itself to be a promising tool to guide practical NW-based solar cell design.

Abreviações

FDTD:

Domínio do tempo de diferença finita

FR:

Filling ratio

FWHM:

Full width at half maximum

NPs:

Nanopartículas

NWs:

Nanofios

Desempenho aprimorado de um novo catalisador PdAu / VGCNF anódico para eletro-oxidação em uma célula de combustível de glicerol Resposta fotovoltaica pronunciada do fototransistor MoTe2 multicamadas com formulário de contato assimétrico