Sistema Teórico de Nanogeradores Triboelétricos em Modo de Contato para Eficiência de Conversão de Alta Energia

Resumo

Como a rápida expansão da eletrônica de próxima geração, fontes de energia portáteis e eficientes se tornou um dos fatores mais importantes que impedem o desenvolvimento do mercado. Nanogeradores triboelétricos (TENGs) são um candidato potencial por suas características insuperáveis. Aqui, analisamos profundamente a potência e a eficiência de conversão dos TENGs de modo de contato considerando todo o processo de conversão de energia. Em primeiro lugar, indo além da análise convencional, uma força de compressão foi introduzida para derivar um perfil de movimento mais versátil, o que proporcionou um melhor entendimento do princípio de funcionamento do processo de separação por contato. Em seguida, analisamos profundamente a influência de vários parâmetros em seu desempenho. Especialmente, os TENGs de eficiência máxima podem ser obtidos sob força ótima. É realista e útil para TENGs mais eficientes. Além disso, esta pesquisa tem uma boa chance de estabelecer padrões para quantificar a eficiência dos TENGs, o que estabelece a base para a industrialização e multifuncionalização da tecnologia dos TENGs.

Histórico

A inteligência artificial e a rede em nuvem estão melhorando gradualmente a qualidade de nossa vida moderna com o rápido desenvolvimento de eletrônicos de última geração para casa inteligente, monitoramento de saúde, entretenimento e monitoramento de ambiente [1,2,3]. Ligar essas grandes quantidades de eletrônicos tornou-se uma missão impossível utilizando as tecnologias de bateria existentes, considerando seu grande tamanho, curta vida útil e, especialmente, problemas de carregamento rápido. Tornou-se uma das barreiras mais importantes para desenvolver uma fonte de energia sustentável adequada para eletrônicos vestíveis [4,5,6].

Atualmente, nanogeradores triboelétricos (TENGs) baseados na triboeletrificação têm demonstrado uma tecnologia atrativa para captação de energia mecânica. É um candidato promissor para a eletrônica vestível por suas inúmeras vantagens, incluindo flexibilidade [7], custo-benefício [8], processo de fabricação simples [9], proteção ambiental [10] e versatilidade [11]. Tem sido amplamente utilizado para coletar energia da energia mecânica do ambiente. Além disso, pode ser utilizado para integração com dispositivos vestíveis para aplicações autoalimentadas [12,13,14]. Por enquanto, muitos métodos têm sido utilizados para aumentar a potência, incluindo morfologia de superfície [15, 16], otimização de material [17, 18], injeção de carga [19, 20], otimização de estrutura [21, 22] e multi-nanogeradores [23, 24]. Apesar do rápido avanço no desempenho de saída, um modelo definitivo para analisar a eficiência de conversão de energia está ausente. Uma série de explicações teóricas foram publicadas para diferentes modos de TENGs [25,26,27]. No entanto, a maioria das análises não discute todo o processo de conversão de energia e se concentra apenas na potência de saída. Mais importante ainda, maior potência de saída não significa maior eficiência de conversão de energia e pode até ser contraproducente. De certa forma, impediu o desenvolvimento de TENGs mais eficientes devido à falta de estudos diretos sobre eficiência de conversão de energia.

Neste trabalho, analisamos sistemática e diretamente a potência e a eficiência de conversão dos TENGs em modo de contato considerando todo o processo. Em primeiro lugar, indo além da análise convencional, uma força de compressão foi introduzida para derivar um perfil de movimento mais versátil, o que proporcionou um melhor entendimento do princípio de funcionamento do processo de separação por contato. Em seguida, de acordo com as equações de movimento, foram apresentadas equações explícitas para o importante desempenho do dispositivo em todo o processo de contato e separação. Finalmente, a influência das propriedades do material, parâmetros estruturais e fator experimental na potência máxima e especialmente na eficiência de conversão de energia foi sistematicamente pesquisada. Podemos obter a máxima eficiência e potência projetando racionalmente parâmetros, especialmente a força de compressão. É realista e útil para TENGs mais eficientes. É importante ressaltar que existe uma boa chance de estabelecer os padrões para quantificar a eficiência dos TENGs, o que estabelece a base para a industrialização e multifuncionalização dos TENGs.

Métodos

O princípio operacional básico dos TENGs é baseado na triboeletrificação e na indução eletrostática. Poderia ser classificado aproximadamente em dois tipos em vista dos materiais de fricção. Devido à função de trabalho e ao atrito, o material dielétrico e o material condutor são escolhidos como os pares triboelétricos. Conforme exibido na Fig. 1, a camada superior consiste no eletrodo superior (TE) e a camada dielétrica pode se mover para cima e para baixo, enquanto o eletrodo inferior (BE) é fixado no substrato. As duas camadas são conectadas com um resistor de carga R . O processo de separação e contato são indicados nas Fig. 1a, b, respectivamente. No processo de separação, os elétrons fluem para o BE a partir do TE e retornam para o TE no processo de contato.

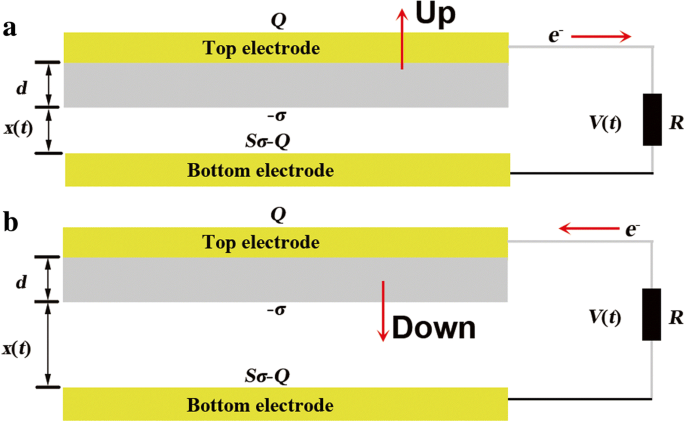
O modelo teórico para o modo de contato dos TENGAs. a Processo de separação e b processo de contato

Sob a força aplicada F , a camada superior fará contato total com a camada inferior. O BE terá cargas triboelétricas positivas com a densidade de carga superficial σ enquanto a camada dielétrica tem as mesmas cargas com sinal oposto. No processo de separação, a camada superior se separa com a camada inferior com uma distância x ( t ) Isso resultará em uma diferença de potencial V ( t ) entre o TE e o BE devido ao campo elétrico. Para compensar V ( t ), os elétrons fluirão entre os dois eletrodos através de R . Portanto, a carga do TE é Q enquanto o BE fica com Sσ - Q . A intensidade do campo elétrico nas duas regiões é dada como segue, de acordo com o teorema de Gauss.

Dentro da camada dielétrica:
$$ {E} _ {\ mathrm {dielétrico}} =- \ frac {Q} {S {\ varejpsilon} _0 {\ varejpsilon} _r} $$ (1)
Dentro do entreferro:
$$ {E} _ {\ mathrm {air}} =\ frac {\ sigma_0-Q / S} {\ varepsilon_0} $$ (2)
onde ε ₀ e ε _r são a permissividade de vácuo e a permissividade relativa, respectivamente.

O V ( t ) deve satisfazer a seguinte equação:
$$ V (t) ={E} _ {\ mathrm {dielétrico}} d + {E} _ {\ mathrm {ar}} x (t) $$ (3)
Da lei de Ohm, o V ( t ) é dado como
$$ V (t) =RI (t) =R \ frac {dQ} {dt} $$ (4)
Mesclando equações, podemos obter
$$ \ frac {dQ} {dt} + \ frac {d_0 + x (t)} {RS {\ varejpsilon} _0} \ times Q =\ frac {\ sigma x (t)} {R {\ varepsilon} _0 } $$ (5)
A Eq. (5) é a equação governante dos TENGs. Pode ser aplicado a todo o processo de separação e contato. É óbvio que x ( t ) é um dos fatores mais importantes dos TENGs. Diferente do trabalho anterior, construímos a equação de movimento prática em vez de assumi-la diretamente. Neste artigo, a equação de movimento em todo o processo é construída com base na força compressiva e na condição experimental.

Resultados e discussão

Sistema não Spring

Em primeiro lugar, consideramos apenas uma força de compressão constante F e a gravidade da camada superior. A equação de movimento pode ser obtida da seguinte forma (consulte o arquivo adicional 1:Nota 1 e Figura S1 no ESM). Na realidade, o x ( t ) sempre tem um valor máximo x _máximo e mínimo zero. Portanto, as equações de movimento são dadas por
$$ \ left \ {\ begin {array} {c} \ x (t) =\ frac {F- mg} {2m} {t} ^ 2, t <\ sqrt {\ frac {2 {x} _ { \ mathrm {max}} m} {F- mg}} \ \\ {} x (t) ={x} _ {\ mathrm {max}}, t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F- mg}} \ end {array} \ right. $$ (6.1) $$ \ left \ {\ begin {array} {c} \ x (t) =\ frac {F + mg} {2m} {t} ^ 2, t <\ sqrt {\ frac {2 { x} _ {\ mathrm {max}} m} {F + mg}} \ \\ {} x (t) =0, t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F + mg}} \ end {array} \ right. $$ (6,2)
As Eqs. (6.1) e (6.2) representam o processo de separação e o processo de contato, respectivamente.

Então podemos obter a carga transferida. (A derivação detalhada está no arquivo Adicional 1:Nota 2 no ESM).

No processo de separação:
$$ {\ displaystyle \ begin {array} {l} Q (t) =\ exp \ left (- \ frac {6m {d} _0t + \ left (F- mg \ right) {t} ^ 3} {6 mRS {\ varejpsilon} _0} \ right) \\ {} \ times {\ int} _0 ^ t \ frac {\ sigma \ left (F- mg \ right) {t} ^ 2} {2 mR {\ varejpsilon} _0 } \ mathit {\ exp} \ frac {6m {d} _0t + \ left (F- mg \ right) {t} ^ 3} {6 mRS {\ varepsilon} _0} dt, t <\ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F- mg}} \ end {array}} $$ (7.1) $$ {\ displaystyle \ begin {array} {l} Q (t) =\ frac {\ sigma S {x} _ {\ mathrm {max}}} {d_0 + {x} _ {\ mathrm {max}}} - \ left (\ frac {\ sigma S {x} _ {\ mathrm {max} }} {d_0 + {x} _ {\ mathrm {max}}} - {Q} _0 \ right) \\ {} \ times \ mathit {\ exp} \ left (- \ frac {d_0 + {x} _ {\ mathrm {max}}} {RS {\ varepsilon} _0} \ left (t- {t} _0 \ right) \ right), t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max} } m} {F- mg}} \ end {array}} $$ (7,2)
onde \ ({t} _0 =\ sqrt {2 {x} _ {\ mathrm {max}} m / \ left (F- mg \ right)} \), e Q ₀ = Q ( t ₀ ) na Eq. (7,1).

No processo de contato:
$$ {\ displaystyle \ begin {array} {l} Q (t) =\ exp \ left (- \ frac {6m {d} _0t + \ left (F + mg \ right) {t} ^ 3} {6 mRS { \ varepsilon} _0} \ right) \\ {} \ times \ left (\ sigma S + {\ int} _0 ^ t \ frac {\ sigma \ left (F + mg \ right) {t} ^ 2} {2 mR { \ varejpsilon} _0} \ mathit {\ exp} \ frac {6m {d} _0t + \ left (F + mg \ right) {t} ^ 3} {6 mRS {\ varepsilon} _0} dt \ right), t <\ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F + mg}} \ end {array}} $$ (8.1) $$ Q (t) ={Q} _0 \ times \ exp \ left (\ frac {d_0 {t} _0- {d} _0t} {RS {\ varepsilon} _0} \ right), t \ ge \ sqrt {\ frac {2 {x} _ {\ mathrm {max}} m} {F + mg}} $$ (8,2)
onde \ ({t} _0 =\ sqrt {2 {x} _ {\ mathrm {max}} m / \ left (F + mg \ right)} \), Q ₀ pode ser calculado atribuindo t = t ₀ na Eq. (8.1).

Portanto, a corrente de saída pode ser derivada como I ( t ) = dQ / dt e V ( t ) = RI ( t )

De acordo com os parâmetros específicos exibidos na Tabela 1, podemos obter os resultados dos cálculos numéricos.

A relação características-tempo em diferentes R em todo o processo é mostrado na Fig. 2. As relações de carga transferida, corrente de saída e tensão de saída em diferentes cargas no processo de contato são mostradas na Fig. 2a, c, e. Os comportamentos são semelhantes aos de estudos anteriores [25]. Mas o processo de separação raramente é estudado. Suponha que as cargas superficiais sejam totalmente transferidas para o TE no processo de separação após um longo tempo. Conforme mostrado na Fig. 2b, na condição de curto-circuito (SC), as cargas no TE podem fluir totalmente de volta para o BE quando a camada superior para de se mover ( t =2 ms). As cobranças não podem diminuir a zero em t =2 ms quando R é mais do que 1 MΩ. Visto que quase todas as cobranças são transferidas para o BE quando R é inferior a 10 MΩ no processo de separação. As cargas transferidas no processo de contato são muito menores do que no processo de separação. Isso contribui para a força motriz relativamente pequena no processo de contato inicial. A relação corrente-tempo de saída é representada graficamente na Fig. 2d. Na condição SC, a corrente de pico é quase a mesma que no processo de separação. Quando R for maior, a curva atual-tempo tem dois valores máximos locais, que estão no início e no final do movimento. E a corrente máxima absoluta cai drasticamente com o aumento da resistência. Os dois valores máximos locais no início e no final do movimento são devidos aos elétrons adequados e ao movimento de alta velocidade, respectivamente. A tensão de saída tem o mesmo perfil com a corrente, mas uma tendência diferente em magnitude, conforme mostrado na Fig. 2f (consulte o arquivo adicional 1:Figura S2 para a relação detalhada no ESM). Deve-se notar que o valor de tensão máxima absoluta é muito menor em comparação com o do processo de separação. Obviamente, a tensão e a corrente não são simétricas no processo de separação e contato. Combinando o processo de separação e contato, a tensão e a corrente de saída são alternadas.

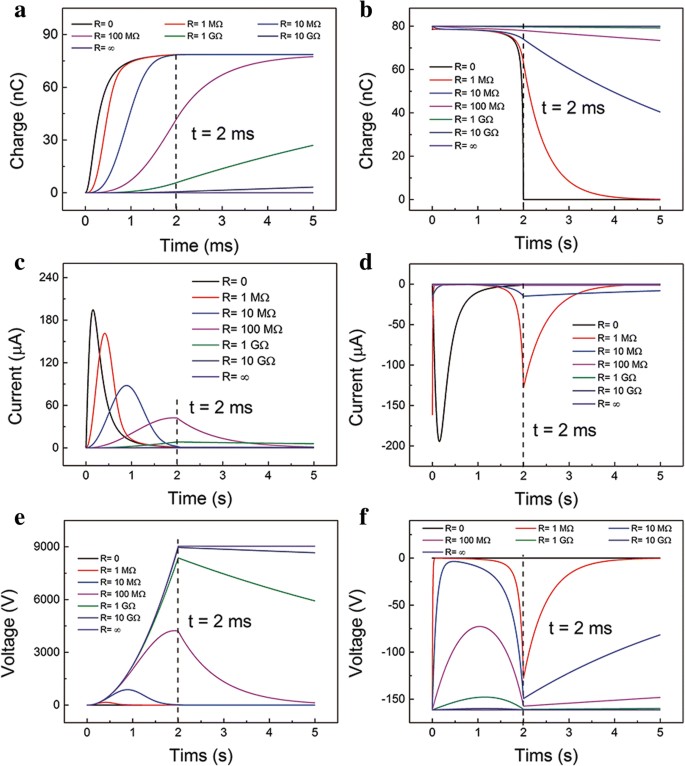
Características de saída calculadas quando o dispositivo está sob uma força de compressão constante F. Relação de tempo de cobrança transferida em R diferente no a processo de contato e b processo de separação. Relacionamento da hora atual em R diferente no c processo de contato e d processo de separação. Relação tensão-tempo em diferentes R no e processo de contato e f processo de separação

Além disso, a influência de vários parâmetros na relação entre a potência máxima P _máximo e a resistência correspondente está representada na Fig. 3. Esses diferentes parâmetros podem ser divididos em material, estrutura e condição do experimento. Por exemplo, os parâmetros do material incluem σ e ε _r . Os parâmetros estruturais são principalmente o tamanho da área S, x _máximo e d. A força compressiva F é o parâmetro do experimento. Pode-se ver que σ, S , F e x _máximo influencia muito o P _máximo , conforme mostrado na Fig. 3a – d. O P _máximo aumenta dramaticamente quando σ, S , F e x _máximo aumentar. O parâmetro σ e S principalmente decidir a quantidade de encargos que podem ser transferidos. Os parâmetros F e x _máximo influenciam principalmente as equações de movimento. A resistência ótima correspondente diminui com x _máximo diminuindo, embora raramente seja afetado por σ, S e F. Além disso, os parâmetros d e ε _r raramente afetam o P _máximo e a resistência correspondente, conforme indicado na Fig. 3e, f. Essa é a espessura efetiva da camada dielétrica d ₀ = d / ε _r que tem pouca influência no desempenho dos TENGs. Podemos ajustar esses parâmetros para controlar a potência máxima. É importante notar que a resistência correspondente é geralmente a resistência de carga da eletrônica.

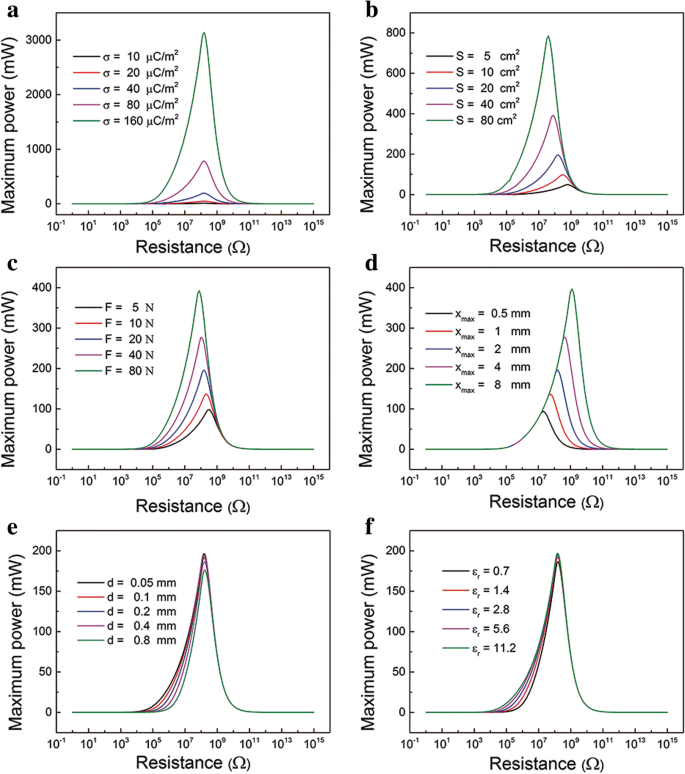
O efeito dos parâmetros em P _máximo e resistência correspondente. Perfil de potência instantâneo com R em diferente a densidade de carga superficial σ, b tamanho da área S , c força compressiva F , d distância máxima de separação x _máximo , e espessura da camada dielétrica d , e f ε _r

Sistema Spring

Para uma condição de experimento mais popular, o sistema de mola está incluído. A força compressiva F é aplicado periodicamente, conforme mostrado na Fig. 4a. No processo de separação ( T = t ₁ ), só resta restaurar a força das molas e da gravidade, então F =0. Durante o processo de contato ( T = t ₂ + t ₃ ), a força compressiva F Está adicionado. E ainda duraria muito depois que as duas camadas entrassem em contato total. As curvas de movimento são mostradas na Fig. 4b. As equações de movimento calculadas e o desempenho de saída são derivados da seguinte forma. (Arquivo adicional 1:Nota 3 no ESM)
$$ \ mathrm {x} (t) ={x} _ {\ mathrm {max}} - {x} _ {\ mathrm {max}} \ mathit {\ cos} \ left ({\ omega} _0t \ right ) $$ (9.1) $$ \ mathrm {x} (t) ={x} _ {\ mathrm {max}} - \ frac {F} {k} + \ frac {F} {k} \ cos \ left ({\ omega} _0t \ right) $$ (9.2)
onde \ ({\ omega} _0 ^ 2 =k / m \). E as Eqs. (9.1) e (9.2) representam o processo de separação e o processo de contato, respectivamente.

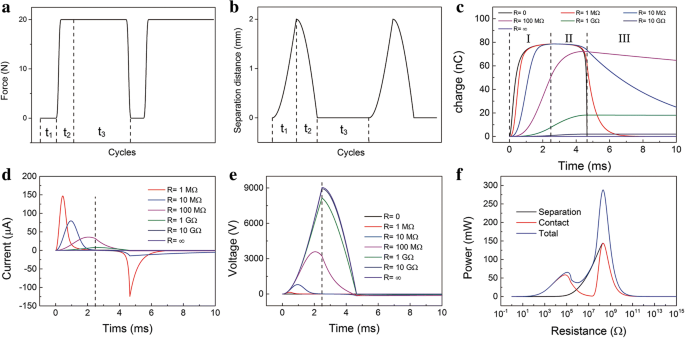
Características calculadas dos TENGs do modo de separação de contato . a A força periódica F . b O movimento periódico da camada superior. c Relação de tempo de cobrança transferida em R diferente no processo de contato e separação. d Relacionamento da hora atual em R diferente no processo de contato e separação. e Relação tensão-tempo em diferentes R no processo de contato e separação. f As relações de potência máxima instantânea com resistências no contato, separação e todo o processo

No processo de separação:
$$ {\ displaystyle \ begin {array} {c} Q (t) ={\ int} _0 ^ t \ frac {\ sigma {x} _ {\ mathrm {max}} \ left (1- \ mathit {\ cos} \ left ({\ omega} _0t \ right) \ right)} {R {\ varepsilon} _0} \ mathit {\ exp} \ left (\ frac {d_0 + {x} _ {\ mathrm {max}}} {RS {\ varepsilon} _0} t- \ frac {x _ {\ mathrm {max}}} {RS {\ varejpsilon} _0 {\ omega} _0} \ mathit {\ sin} \ left ({\ omega} _0t \ direita) \ direita) dt \\ {} \ times \ mathit {\ exp} \ left (- \ frac {d_0 + {x} _ {\ mathrm {max}}} {RS {\ varepsilon} _0} t + \ frac { x _ {\ mathrm {max}}} {RS {\ varejpsilon} _0 {\ omega} _0} \ mathit {\ sin} \ left ({\ omega} _0t \ right) \ right), t <{t} _1 \ fim {array}} $$ (10)
No processo de contato:
$$ {\ displaystyle \ begin {array} {l} Q (t) =\ mathit {\ exp} \ left (- \ frac {d_0 + {x} _ {\ mathrm {max}} - \ frac {F} { k}} {RS {\ varejpsilon} _0} t + \ frac {Fsin \ left ({\ omega} _0t \ right)} {kRS {\ varejpsilon} _0 {\ omega} _0} \ right) \\ {} \ times \ left \ {{q} _0 + {\ int} _0 ^ t \ mathit {\ exp} \ left (\ frac {d_0 + {x} _ {\ mathrm {max}} - \ frac {F} {k}} { RS {\ varepsilon} _0} t- \ frac {Fsin \ left ({\ omega} _0t \ right)} {kRS {\ varepsilon} _0 {\ omega} _0} \ right) \ right. \ \\ {} \ \\ {} \ times \ left. \ frac {\ sigma \ left ({x} _ {\ mathrm {max}} - \ frac {F} {k} + \ frac {F} {k} \ cos \ left ({\ omega} _0t \ right) \ right)} {R {\ varepsilon} _0} dt \ right \}, t <{t} _2 \ \ end {array}} $$ (11) $$ Q (t ) ={Q} _0 \ times \ mathit {\ exp} \ left (\ frac {d_0} {RS {\ varepsilon} _0} \ left ({t} _0-t \ right) \ right), t \ ge { t} _3 $$ (12)
onde q ₀ são as cargas transferidas do BE para o TE no processo de separação.

A corrente e a tensão de saída podem ser calculadas como I ( t ) = dQ / dt e V ( t ) = RI ( t )

A relação de tempo de cobrança transferida em R diferente no processo completo está representado na Fig. 4c. O processo de transferência de carga é dividido em três regiões, que correspondem à força periódica. A região I representa o processo de separação e o processo de contato contém as regiões II e III. Na região I, os encargos são transferidos para o TE do BE. Os encargos no TE continuam aumentando. Na região II, a direção do fluxo de carga está relacionada à resistência. As cargas no TE continuam a aumentar quando a resistência é grande ( R ≥ 1 GΩ). Aumenta ao máximo e depois diminui quando a resistência é baixa ( R ≤ 100 MΩ). Especialmente, quando R =0, as cobranças continuarão diminuindo na região II. Na região III, os encargos no TE continuam diminuindo. A corrente de saída correspondente em todo o processo é mostrada na Fig. 4d. A corrente no processo de separação e contato tem o sinal oposto. Normalmente, o valor máximo da corrente no processo de separação é um pouco maior do que no processo de contato. Curiosamente, no processo de contato, o valor atual máximo absoluto aparece no início do processo de contato ou no momento em que eles estão apenas em contato. Quando a resistência é grande, ela aparece no início do processo de contato, vice-versa. A tensão de saída aumenta com o tempo e depois diminui, conforme mostrado na Fig. 4e. A tensão de saída apareceria como um valor negativo no processo de contato. E o valor absoluto é muito menor do que no processo de separação. Esses números são consistentes com os gráficos experimentais medidos na literatura. A corrente de saída medida está alternando obviamente, e a tensão de saída medida é geralmente de pico agudo. As relações da potência máxima instantânea com as resistências no contato, separação e todo o processo são mostradas na Fig. 4f. O TENGs atinge sua potência instantânea máxima absoluta em torno de 200 MΩ no processo de separação e contato. Enquanto no processo de contato, ele tem um valor máximo local adicional em torno de 0,1 MΩ. Portanto, em todo o processo, a potência instantânea atinge seu valor máximo em torno de 200 MΩ. Percebe-se que a curva de potência do processo de contato se sobrepõe à do processo de separação quando a resistência é grande. Porque o valor máximo atual aparece na interseção dos dois processos quando R ≥ 200 MΩ.

Além disso, os resultados calculados de P _máximo e a resistência ótima correspondente são plotadas na Fig. 5. Conforme indicado na Fig. 5a-c, a potência instantânea máxima aumenta conforme os parâmetros x _máximo , S e k aumentar. Isso pode contribuir para a velocidade de transferência mais rápida dos elétrons. Ao mesmo tempo, a resistência ótima correspondente também muda. A resistência ótima diminui com S e k aumentando, mas a tendência inversa com x _máximo . A influência dos parâmetros σ no P _máximo e a resistência ótima é mostrada na Fig. 5d. O P _máximo aumenta rapidamente com o aumento de σ, enquanto a resistência ótima se mantém constante. A resistência ótima também não é afetada por ε _r . Mas como ε _r aumenta, a potência instantânea máxima aumenta e depois fica saturada. O F quase não tem influência na potência instantânea máxima e na resistência ideal. Em todo o processo de contato e separação, o F afeta apenas o processo de contato. Portanto, a corrente máxima no processo de separação permanece a mesma. Conforme ilustrado na Fig. 5f, a potência instantânea máxima não muda. Isso é diferente do sistema sem molas. No sistema sem mola, o F afeta diretamente o processo de separação, afetando assim a potência máxima.

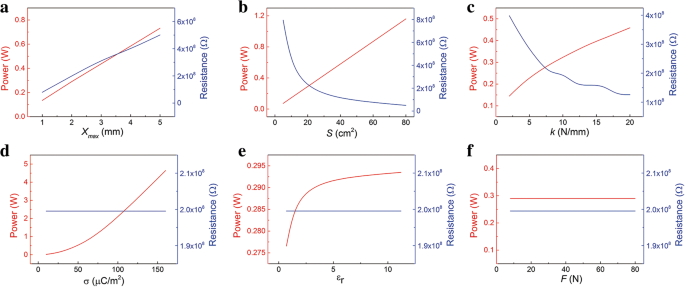
Influência dos parâmetros no P _máximo e resistência correspondente em um ciclo. A relação de P _máximo e a resistência correspondente com os parâmetros a x _máximo , b S , c k , d σ, e ε _r , e f F

Em uma palavra, o P _máximo pode ser aumentado aumentando a distância máxima de separação x _máximo , área S , coeficiente de mola k , permissividade relativa da camada dielétrica ε _r , e especialmente densidade de carga superficial σ. Por exemplo, parâmetros de material como ε _r e σ são geralmente otimizados para obter maior potência [28, 29]. Embora a resistência ideal possa ser ajustada pelos parâmetros x _máximo , S e k . O P _máximo e a resistência ótima depende principalmente do material e dos parâmetros estruturais.

Eficiência de conversão η de TENGs

Às vezes, estamos mais preocupados com P _máximo que ignoramos o η . A eficiência é um parâmetro importante para avaliar uma fonte de energia. η é definida como a razão entre a energia elétrica de saída e a energia mecânica de entrada. Aqui, pesquisamos de forma sistemática e direta a influência desses parâmetros na eficiência.

A energia elétrica e a energia mecânica são obtidas de acordo com o pulso de corrente no R ótimo . A energia elétrica de saída é dada por
$$ {E} _ {\ mathrm {electric}} ={\ int} _ {t _ {\ mathrm {start}}} ^ {t _ {\ mathrm {end}}} {I} ^ 2 Rdt $$ (13 )
onde o intervalo de tempo entre t _start e t _fim expressa todo um processo de contato e separação.

A energia mecânica calculada é
$$ {E} _ {\ mathrm {Mechanical}} =F \ times S $$ (14)
Assim, o η é calculado da seguinte forma
$$ \ eta =\ frac {E _ {\ mathrm {elétrico}}} {E _ {\ mathrm {mecânico}}} \ vezes 100 \% $$ (15)
A relação de η com x _máximo foi mostrado na Fig. 6a. Como x _máximo aumenta, a eficiência η aumenta e depois fica saturado gradualmente. Sabemos que a energia mecânica e a potência máxima são proporcionais a x _máximo . No entanto, aumentando x _máximo mudará a nitidez da curva de tempo atual. Isso significa que a taxa de crescimento diminuirá quando x _máximo é maior. A influência dos parâmetros S , k , e σ em η são mostrados na Fig. 6b – d. A tendência de aumento da eficiência η com esses parâmetros é semelhante ao da potência máxima. A eficiência η aumenta gradualmente com o S e k aumentando. Notavelmente, o σ pode influenciar muito a eficiência η . O parâmetro ε _r é difícil de mudar e, felizmente, quase não afeta η como mostrado na Fig. 6e. Conforme mostrado na Fig. 6f, a eficiência η diminui rapidamente como F aumenta. Isso contribui principalmente para o aumento da energia mecânica. Obviamente, a eficiência é relativamente baixa. Felizmente, podemos aumentar muito a eficiência melhorando σ.

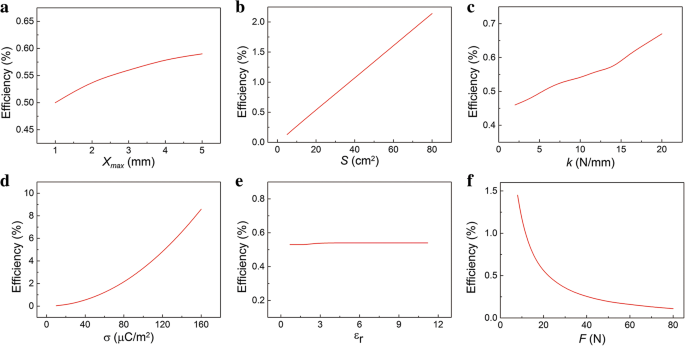
Eficiência de conversão η de TENG. A relação da eficiência de conversão calculada com os parâmetros a x _máximo , b S , c k , d σ, e ε _r , e f F

Na situação prática, no entanto, o F pode afetar o parâmetro σ [30]. Abaixo de F pequeno , as duas camadas estão em contato parcial. As duas camadas podem obter melhor contato como F aumenta. Em seguida, o parâmetro F quase pode afetar a densidade de carga superficial σ. Ou seja, o σ aumenta com o F então fica saturado, como mostrado na Fig. 7a. Portanto, recalculamos a relação entre o desempenho de saída e a força de compressão F . A influência de F na corrente máxima, tensão e potência instantânea são mostrados na Fig. 7b – d, respectivamente. Eles têm uma relação semelhante com F . Por exemplo, a tensão de saída aumenta com F aumentando e depois mantendo constante, o que é consistente com os dados de experimentos na literatura [31, 32]. A influência de F sobre a energia elétrica é mostrado na Fig. 7e. Deve-se notar que existe um ponto de inflexão na curva. A energia elétrica de saída aumenta com F aumentando e depois diminuindo ligeiramente. A ligeira queda da energia elétrica de saída é devido ao processo de contato mais curto sob maior F . Sob pequena força de compressão, o F é proporcional ao σ, o que resulta em uma maior saída de energia elétrica. No entanto, sob uma grande força de compressão, o σ fica saturado. As cargas transferidas no processo de separação se mantêm constantes enquanto diminuem no processo de contato sob maior força de compressão. Portanto, a energia elétrica de saída em todo o processo de separação e contato cai ligeiramente. A relação de η e F é apresentado na Fig. 7f. Curiosamente, o η - F curva é um pico agudo e o valor máximo apareceu em F ≈ 50 N. A entrada E _mecânico é proporcional a F , enquanto E _mecânico é muito maior do que a saída E _elétrica . Abaixo de F pequeno , a taxa de crescimento de E _elétrica é mais rápido que E _mecânico devido ao rápido aumento em σ. No entanto, sob grande F , a diminuição de E _elétrica e aumento de E _mecânico resultar em uma eficiência menor. O ponto de inflexão na relação entre eficiência de conversão de energia e força compressiva é importante no projeto de uma fonte de energia eficaz.

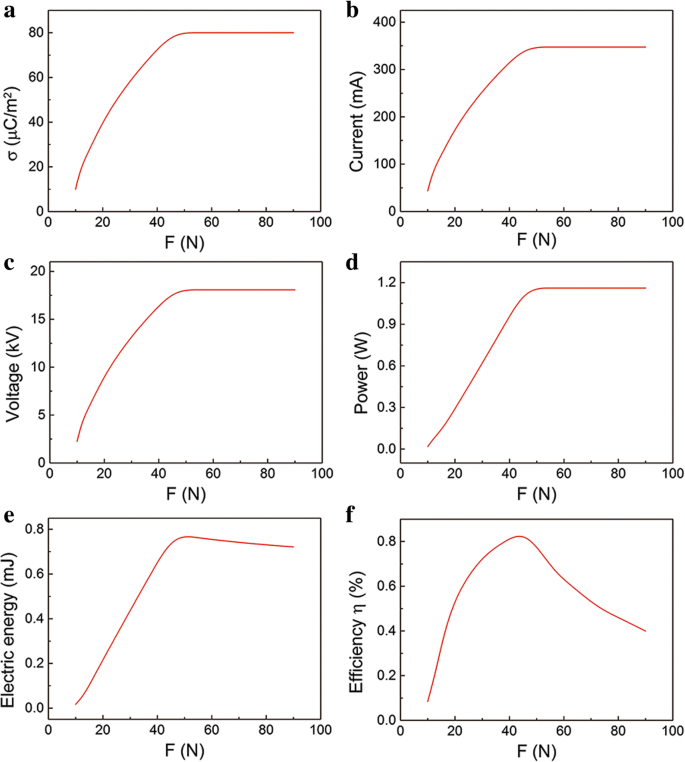
A relação do desempenho de saída com a força de compressão F em situação prática. a A influência da força de compressão F em a densidade de carga superficial σ, b corrente máxima, c tensão máxima, d potência instantânea máxima, e energia elétrica, e f eficiência

A fim de obter maior desempenho de saída, como potência atual e instantânea, uma grande força de compressão F geralmente é aplicado. Mas isso pode causar uma baixa eficiência de conversão. De acordo com a análise acima, podemos escolher um F racional para obter a alta potência, bem como a eficiência de conversão.

Conclusão

Em conclusão, introduzimos uma abordagem prática para analisar sistemicamente e diretamente a eficiência de conversão de TENGs de modo de contato. Indo além da análise convencional, uma força de compressão foi introduzida para derivar um perfil de movimento mais versátil, o que proporcionou um melhor entendimento do princípio de operação do processo de separação por contato. Foram apresentadas as equações explícitas para o importante desempenho do dispositivo em todo o processo de separação e contato, ao contrário das análises convencionais que focam apenas no processo de separação. Em primeiro lugar, analisamos a relação do desempenho de saída com o material, a estrutura e os parâmetros experimentais, principalmente para uma maior potência de saída. Então, é importante que estudamos sistemática e profundamente a influência desses parâmetros na eficiência de conversão de energia em todo o processo. É importante notar que um ponto de inflexão foi encontrado na relação entre a eficiência de conversão e a força de compressão. Os TENGs com alta potência de saída e alta eficiência de conversão podem ser obtidos ao mesmo tempo sob força ideal. É realista e útil para TENGs mais eficientes. É importante ressaltar que há uma boa chance de estabelecer os padrões para quantificar a eficiência dos TENGs, o que estabelece a base para a industrialização e multifuncionalização dos TENGs.

Abreviações

BE:: Eletrodo inferior
TE:: Eletrodo superior
TENGs:: Nanogeradores triboelétricos

Investigação sobre o comportamento nanomecânico do gradiente do esmalte com fluorose dentária Nova entrega de mitoxantrona com nanopartículas de pululano modificadas hidrofobicamente para inibir as células cancerosas da bexiga e o efeito do tamanho do nanofármaco na eficiência da inibiçã…

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias