Influência de luxações no índice de refração de AlN por campo de tensão em nanoescala

Resumo

O índice de refração de AlN tem uma influência direta em dispositivos optoeletrônicos ultravioleta profundos baseados em AlGaN, como a eficiência quântica externa de dispositivos emissores de luz. Revelar a dependência do índice de refração de AlN nas luxações de rosqueamento é significativo, uma vez que as luxações de rosqueamento de alta densidade geralmente existem em AlN. Neste artigo, o efeito de diferentes densidades de deslocamento no índice de refração do AlN é investigado. Com o aumento das densidades de deslocamento de 4,24 × 10 ⁸ para 3,48 × 10 ⁹ cm ^{- 2} , o índice de refração de AlN diminui de 2,2508 para 2,2102 a 280 nm. Um estudo posterior demonstra que o campo de deformação em nanoescala em torno dos deslocamentos altera a propagação da luz e, portanto, diminui o índice de refração do AlN. Este estudo será benéfico para o projeto de dispositivos optoeletrônicos e, assim, realizar dispositivos optoeletrônicos ultravioleta profundos de alto desempenho.

Introdução

Os materiais à base de AlN são materiais promissores para fabricar dispositivos optoeletrônicos ultravioleta profundo (DUV), como diodos emissores de luz (LEDs) [1,2,3,4,5], diodos laser [6,7,8] e fotodetectores [ 9, 10] devido ao bandgap direto sintonizável de 3,4 a 6,2 eV [11]. O índice de refração do AlN tem efeitos diretos no desempenho dos dispositivos optoeletrônicos. Para LEDs, o índice de refração de AlN tem impactos na eficiência do extrato de luz (LEE) porque o ângulo de reflexão interno total é determinado pela diferença do índice de refração entre a camada de AlN e outra região, que é o principal fator limitante para a quantidade de saída de luz. Uma vez que a eficiência quântica externa (EQE) é o produto da eficiência quântica interna e o LEE, o índice de refração de AlN afetará o EQE dos LEDs. Além disso, o índice de refração desempenha um papel fundamental no projeto de estruturas de guia de ondas, como o refletor de Bragg distribuído (DBR) [12,13,14], cuja refletividade é sensível ao índice de refração. Portanto, revelar os fatores que afetam o índice de refração de AlN é importante. Pode ser aprendido a partir de estudos anteriores que o índice de refração de AlN pode ser afetado por muitos fatores, incluindo temperatura, pressão e bandgap. O índice de refração do AlN aumenta com a temperatura mais alta [15] e a pressão mais baixa [16]. Para material baseado em AlN, o índice de refração torna-se menor com o aumento do bandgap [17]. Além disso, os deslocamentos em semicondutores têm grande influência nas propriedades dos semicondutores e no desempenho dos dispositivos. Os deslocamentos irão liberar o estresse nos materiais [18]. Eles também afetarão a corrente escura e a responsividade dos fotodetectores [19] e influenciarão o IQE de vários poços quânticos [11, 20] e assim por diante. No entanto, poucas pesquisas enfocam a influência de diferentes densidades de deslocamento de threading (TDDs) no índice de refração de AlN, embora haja altos TDDs em materiais de AlN, que geralmente variam de 10 ⁸ a 10 ⁹ cm ^{- 2} pedidos de relatórios recentes [21,22,23]. Investigar a correlação entre os TDDs e o índice de refração do AlN é a chave para otimizar o desempenho dos dispositivos optoeletrônicos. Neste artigo, a dependência de diferentes TDDs no índice de refração do AlN foi estudada. Os diferentes comprimentos de onda de fótons são usados, como 633 nm, 365 nm e 280 nm. Os resultados mostram que os deslocamentos levam à diminuição do índice de refração do AlN. Os resultados irão beneficiar o projeto e simulação de dispositivos optoeletrônicos baseados em AlN, como LEDs DUV e estruturas DBR.

Métodos

Para estudar a relação entre os deslocamentos e o índice de refração de AlN, modelos de AlN foram cultivados por deposição de vapor químico orgânico de metal (MOCVD) em substratos de safira c e, em seguida, recozidos em diferentes temperaturas para obter amostras de AlN com diferentes densidades de deslocamento.

Ao cultivar modelos de AlN por MOCVD, trimetilalumínio e amônia foram usados como gases precursores. O hidrogênio foi usado como gás de arraste. A pressão durante o crescimento foi mantida em 40 mbar. A temperatura de crescimento e o tempo da camada de nucleação é de cerca de 955 ° C por 150 se, em seguida, aumentada para 1280 ° C para crescimento de AlN em alta temperatura (HT). Após 15 min de crescimento de AlN em alta temperatura, uma intercamada de AlN foi cultivada a 1050 ° C por 160 s. Finalmente, a temperatura de crescimento foi elevada para 1280 ° C para crescer HT AlN espesso por 50 min. A espessura total do filme de AlN é de cerca de 1,1 μm.

Após o crescimento da camada de AlN por MOCVD, os modelos de AlN foram recozidos ex situ a 1500 ° C, 1600 ° C, 1700 ° C e 1750 ° C por 1 h, respectivamente. A camada de AlN sem recozimento foi marcada como amostra 1, e as amostras após recozimento de 1500 ° C a 1750 ° C foram marcadas como amostras 2 a 5. A difração de raios-X (XRD) foi usada para medir os TDDs em amostras de AlN, e a medição elipsométrica espectroscópica (SE) foi realizada para medir o índice de refração. Os espectros de deslocamento Raman foram adotados para caracterizar o estado de tensão de modelos de AlN.

Resultados e discussão

As Figuras 1 aeb mostram as curvas de balanço plano XRD (XRC) (0002) e (10-12) das cinco amostras de AlN. Pode ser observado que a largura total na metade do máximo (FWHM) do (0002) plano XRC diminui ligeiramente e o FWHM do (10-12) plano XRC diminui muito da amostra 1 para a amostra 5. A densidade de deslocamentos com parafuso e borda o componente pode ser calculado usando o FWHM de (0002) e (10-12) plano XRC de acordo com a fórmula (1) e (2):[24, 25].
$$ {\ rho} _ {\ mathrm {s}} ={\ beta _ {(0002)}} ^ 2 / \ left (2 \ pi \ ln 2 \ times {\ left | {b} _c \ right |} ^ 2 \ right) $$ (1) $$ {\ rho} _ {\ mathrm {e}} ={\ beta _ {\ left (10-12 \ right)}} ^ 2 / \ left (2 \ pi \ ln 2 \ times {\ left | {b} _a \ right |} ^ 2 \ right) $$ (2)

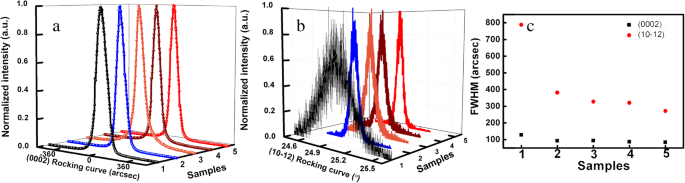
a O (0002) plano XRC de cinco amostras de AlN. b O plano (10-12) XRC de cinco amostras de AlN. c O FWHM de (0002, 10-12) plano XRC; o círculo vermelho significa o FWHM do plano (10-12) e o quadrado preto representa o FWHM do plano (0002)

onde ρ _s e ρ _e representam a densidade do deslocamento com parafuso e componente de borda, respectivamente. β é o FWHM do XRC. | b _c | é igual à constante de rede axial c, e | b _a | é igual a uma constante de rede axial de AlN. O FWHM de (0002) e (10-12) plano XRC são exibidos na Fig. 1c para as cinco amostras de AlN e os TDDs calculados das cinco amostras de AlN são mostrados na Tabela 1.

Os dados experimentais SE das cinco amostras são ajustados pelo software CompleteEASE (J.A. Woollam Inc.) usando um modelo de semicondutor paramétrico, que pode reproduzir as propriedades ópticas de semicondutores de gap direto de forma eficaz [26]. A Figura 2a mostra as curvas experimentais parciais e de ajuste das cinco amostras. O erro quadrático médio (MSE) das cinco amostras é 8,139, 8,536, 9,175, 10,560 e 9,821, respectivamente, o que confirma os bons resultados de ajuste. Todos os dados e resultados de ajuste são fornecidos no arquivo adicional 1.

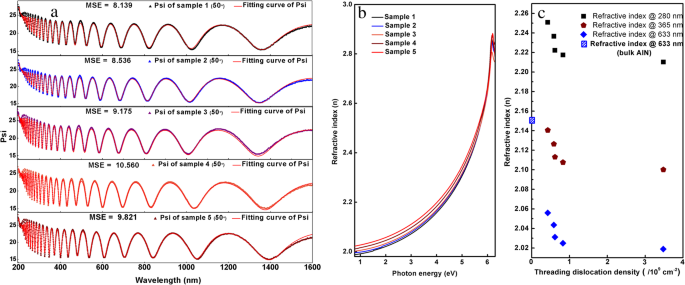
a Dados experimentais parciais de medição SE e curvas de ajuste. b A curva do índice de refração. c Índice de refração vs. diferentes TDDs em 280 nm, 365 nm e 633 nm

As curvas de índice de refração das cinco amostras podem ser obtidas a partir de resultados de ajuste, conforme mostrado na Fig. 2b. Quando a energia do fóton é menor do que o bandgap do AlN (cerca de 6,2 eV), o índice de refração aumenta com o aumento da energia do fóton para todas as cinco amostras. Porém, quando a energia do fóton é maior que 6,2 eV, o índice de refração diminui com o aumento da energia do fóton. Este fenômeno pode ser descrito pela relação de dispersão Kramers-Krőnig. Com a diminuição dos TDDs em AlN, o índice de refração aumenta de 2,019 para 2,056 em 633 nm, que é mais próximo do AlN em massa (2,15 em 633 nm [27]). Isso significa que os deslocamentos no AlN tornam o índice de refração menor do que o do cristal de AlN em massa.

A relação entre o índice de refração e TDDs em 4,42 eV (280 nm, UV cego solar), 3,40 eV (365 nm, bandgap de GaN) e 1,96 eV (633 nm) são mostrados na Fig. 2c, bem como na Tabela 1 Pode-se observar que o índice de refração do AlN diminui com o aumento dos TDDs. Com o aumento das densidades de deslocamento de 4,24 × 10 ⁸ para 3,48 × 10 ⁹ cm ^{- 2} , o índice de refração de AlN diminui de 2,2508 para 2,2102 a 280 nm.

Para revelar o mecanismo de como os deslocamentos mudam o índice de refração do AlN, o campo de deformação induzido pelos deslocamentos é estudado. A relação entre o índice de refração e a deformação preenchida é descrita pela fórmula (3) [28]:
$$ \ Delta {\ left (\ frac {1} {n ^ 2} \ right)} _ i =PS =\ sum \ limits_ {ij} {p} _ {ij} {s} _j $$ (3)
Na fórmula, p _ij são o tensor elasto-óptico e S é a presença de tensão. A matriz de constantes fotoelásticas P de wurtzite AlN é mostrado como expressão (4) [29, 30].
$$ p =\ left (\ begin {array} {l} -0,1 \ kern1.75em -0,027 \ kern0.75em -0,019 \ kern1em 0 \ kern3em 0 \ kern2.75em 0 \\ {} -0,027 \ kern0,5em -0.1 \ kern2em -0.019 \ kern1em 0 \ kern3em 0 \ kern2.75em 0 \\ {} -0.019 \ kern0.5em -0.019 \ kern1em -0.107 \ kern1em 0 \ kern3em 0 \ kern2.75em 0 \\ {} 0 \ kern2.75em 0 \ kern3em 0 \ kern3.5em -0.032 \ kern0.75em 0 \ kern2.75em 0 \\ {} 0 \ kern2.75em 0 \ kern3em 0 \ kern3.5em 0 \ kern3em -0.032 \ kern0.5em 0 \\ {} 0 \ kern2.75em 0 \ kern3em 0 \ kern3.5em 0 \ kern3em 0 \ kern2.75em -0,037 \ end {array} \ right) $$ (4)
As matrizes de campo de deformações de deslocamento do parafuso e deslocamento da borda em AlN são consideradas. Os modelos de anéis cilíndricos dos dois tipos de deslocamento são descritos na Fig. 3. De acordo com os modelos, a distribuição do campo de deformações em torno de um único deslocamento pode ser obtida [31, 32].

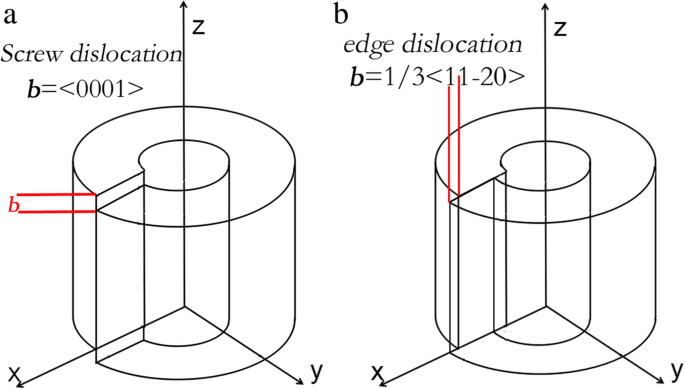
Modelo de anel cilíndrico de a deslocamento do parafuso e b deslocamento de borda

O campo de tensão em torno do deslocamento do parafuso da unidade pode ser escrito como:
$$ {e} _ {xz} ={e} _ {zx} =- \ frac {b} {4 \ pi} \ frac {y} {\ left ({x} ^ 2 + {y} ^ 2 \ direita)} $$ (5) $$ {e} _ {yz} ={e} _ {zy} =\ frac {b} {4 \ pi} \ frac {x} {\ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (5a) $$ {e} _ {xx} ={e} _ {yy} ={e} _ {zz} ={e} _ {xy} ={ e} _ {yx} =0 $$ (5b)
O campo de tensão em torno do deslocamento da borda da unidade pode ser escrito como:
$$ {e} _ {xx} =- \ frac {b} {4 \ pi \ left (1-v \ right)} \ frac {y \ left ({x} ^ 2- {y} ^ 2 \ right )} {{\ left ({x} ^ 2 + {y} ^ 2 \ right)} ^ 2} - \ frac {b} {2 \ pi} \ frac {y} {\ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (6) $$ {e} _ {yy} =\ frac {b} {4 \ pi \ left (1-v \ right)} \ frac {y \ left (3 {x} ^ 2 + {y} ^ 2 \ right)} {{\ left ({x} ^ 2 + {y} ^ 2 \ right)} ^ 2} - \ frac {b} {2 \ pi } \ frac {y} {\ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (6a) $$ {e} _ {zz} =\ frac {b \ left (\ lambda - 2 v \ lambda -2 Gv \ right)} {2 \ pi \ left (2G + \ lambda \ right) \ left (1-v \ right)} \ frac {y} {x ^ 2 + {y} ^ 2} $$ (6b) $$ {e} _ {xy} ={e} _ {yx} =\ frac {b} {4 \ pi \ left (1-v \ right)} \ frac {x \ left ({ x} ^ 2- {y} ^ 2 \ right)} {{\ left ({x} ^ 2 + {y} ^ 2 \ right)} ^ 2} $$ (6c) $$ {e} _ {xz } ={e} _ {zx} ={e} _ {yz} ={e} _ {zy} =0 $$ (6d)
onde b é o comprimento do vetor de Burgers de deslocamento da unidade e e representa a tensão em torno do deslocamento. G =121 GPa é o módulo de cisalhamento de wurtzite AlN; λ =117,1 GPa e v =0,241 são a constante de coxa e o coeficiente de Poisson [33, 34], respectivamente. De acordo com a correspondência entre e _ij e S _k ( eu , j = x , y , z ; k =1,2,3 ... 6) [35], convertemos o campo de deformação em formação de matriz como abaixo para apresentar ainda a mudança do índice de refração causada pelos deslocamentos.
$$ {S} _ {\ mathrm {borda}} =\ left ({S} _1 \ kern0.5em {S} _2 \ kern0.5em {S} _3 \ kern0.5em 0 \ kern0.5em 0 \ kern0. 5em {S} _6 \ right) $$ (7) $$ {S} _ {\ mathrm {screw}} =\ left (0 \ kern0.5em 0 \ kern0.5em 0 \ kern0.5em {S} _4 \ {S} _5 \ kern0.5em 0 \ right) $$ (8)
Colocando as matrizes (7) e (8) na fórmula (3), podemos obter a expressão de Δ n causado pelo parafuso da unidade e deslocamento da borda da unidade.
$$ \ Delta {\ left (\ frac {1} {n ^ 2} \ right)} _ {\ mathrm {screw}} ={\ left (\ frac {1} {n_1 ^ 2} - \ frac {1 } {n_0 ^ 2} \ right)} _ {\ mathrm {screw}} =- 0,032 \ left ({S} _4 + {S} _5 \ right) =- 0,008 \ frac {b \ left (xy \ right)} {\ pi \ left ({x} ^ 2 + {y} ^ 2 \ right)} $$ (9) $$ \ Delta {\ left (\ frac {1} {n ^ 2} \ right)} _ { \ mathrm {edge}} ={\ left (\ frac {1} {n_1 ^ 2} - \ frac {1} {n_0 ^ 2} \ right)} _ {\ mathrm {edge}} =- 0,146 \ left ( {S} _1 + {S} _2 \ right) -0,145 {S} _3-0,037 {S} _6 =\ hbox {-} 0,146 \ left (\ frac {b} {4 \ pi \ left (1-v \ right )} - \ frac {b} {2 \ pi} \ right) \ frac {2y} {x ^ 2 + {y} ^ 2} -0,145 \ frac {b \ left (\ lambda -2 \ lambda v-2 Gv \ right)} {2 \ pi \ left (2G + \ lambda \ right) \ left (1-v \ right)} \ frac {y} {x ^ 2 + {y} ^ 2} -0,037 \ frac {b } {4 \ pi \ left (1-v \ right)} \ frac {x \ left ({x} ^ 2- {y} ^ 2 \ right)} {{\ left ({x} ^ 2 + {y } ^ 2 \ right)} ^ 2} $$ (10)
Com base no cálculo, as distribuições do índice de refração (tome o índice de refração a 633 nm como exemplo) em torno do parafuso unitário e dos deslocamentos da borda unitária são mostradas na Fig. 4. Isso mostra que o índice de refração em torno do deslocamento muda ao longo da direção radial do núcleo de deslocamento, que pode ser considerado um meio não homogêneo. Assim, a propagação da luz em AlN será correspondentemente influenciada por TDDs. A dispersão e a interferência acontecerão [36] quando a luz passar por esses campos refrativos em torno dos deslocamentos. Como resultado, o índice de refração de AlN será alterado, que é a correspondência com a matriz de espalhamento do meio não homogêneo [37].

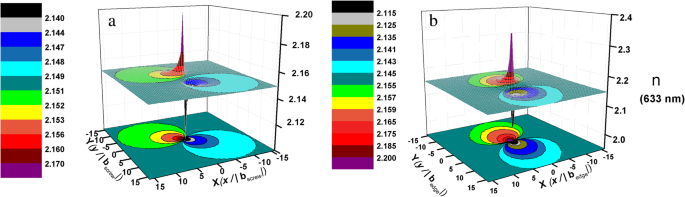
A distribuição do índice de refração em 633 nm em torno de a deslocamento do parafuso da unidade e b deslocamento da borda da unidade

Conforme mencionado na seção “Introdução”, outros fatores de influência devem ser eliminados para provar que o índice de refração é realmente influenciado por deslocamentos. Todas as amostras foram medidas à temperatura ambiente para evitar a influência da temperatura. Para evitar a influência da tensão no material de AlN, o espectro Raman foi usado para confirmar a tensão em AlN e os resultados são mostrados na Fig. 5. O E _g pico modo de safira em 750 cm ^{- 1} é considerado calibração. O pico de deslocamento Raman de AlN E ₂ ( h ) muda para o azul com a diminuição dos TDDs, conforme mostrado na Tabela 1. A mudança para o azul de E ₂ ( h ) pico significa que o AlN sofre mais e mais estresse de compressão do substrato de safira. No entanto, com o aumento da tensão compressiva, o índice de refração torna-se mais próximo do AlN bulk a 633 nm. Pode-se obter claramente que o estresse do AlN sofre com substratos heterogêneos e tem pouca influência no índice de refração. Evidência adicional para apoiar a conclusão é que o índice de refração do AlN também é menor do que o do AlN bulk quando o AlN sofre tensão de tração do substrato de Si [38], que é o mesmo que a condição em que o AlN sofre tensão de compressão neste trabalho. Este fenômeno pode ser atribuído ao fato de que a tensão de AlN sofre com substratos é muito pequena para fazer uma mudança significativa no índice de refração de AlN. Como resultado, em comparação com a influência de outros fatores, o efeito da tensão dos substratos no índice de refração do AlN pode ser desprezado.

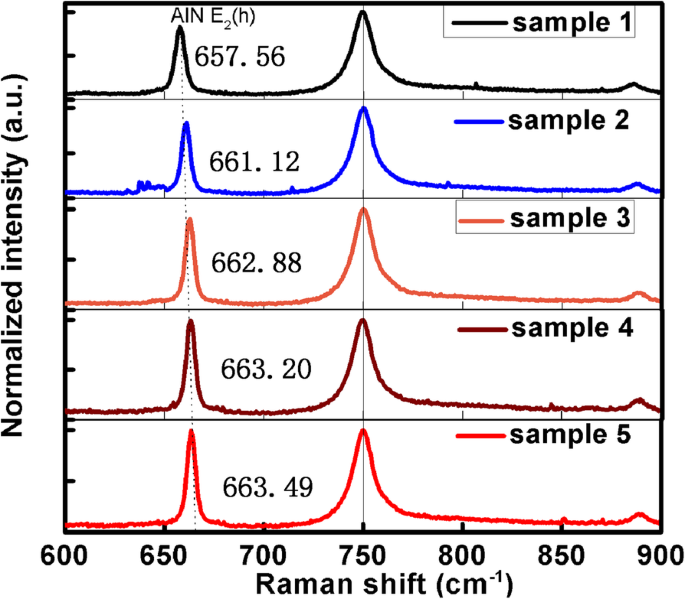
Espectros de deslocamento Raman das cinco amostras

O bandgap das cinco amostras também é calculado aqui. O coeficiente de absorção óptica α é extraído dos resultados de ajuste SE e, em seguida, o bandgap E _g é calculado com base na fórmula abaixo [39]:
$$ {\ left (\ alpha E \ right)} ^ 2 =\ left \ {\ begin {array} {c} C \ left (E- {E} _g \ right) \ kern0.75em \ left (E \ ge {E} _g \ right) \\ {} 0 \ kern4.75em \ left (E <{E} _g \ right) \ end {array} \ right. $$ (11)
O enredo de ( αE ) ² vs. E é apresentado como Fig. 6. A interceptação do x -axis é o valor de E _g . A partir da interceptação de curvas de ajuste no x -eixo, o aumento do bandgap de 6,1106 para 6,1536 eV para a amostra 1 até a amostra 5 é mostrado na Fig. 6. A relação entre o índice de refração e o bandgap é mostrado abaixo [16].
$$ n (E) ={\ esquerda [a {\ esquerda (\ frac {E} {E_g} \ direita)} ^ 2 \ esquerda (2 - {\ esquerda (1+ \ frac {E} {E_g} \ direita)} ^ {0,5} - {\ esquerda (1- \ frac {E} {E_g} \ direita)} ^ {0,5} \ direita) + b \ direita]} ^ {0,5} $$ (12)

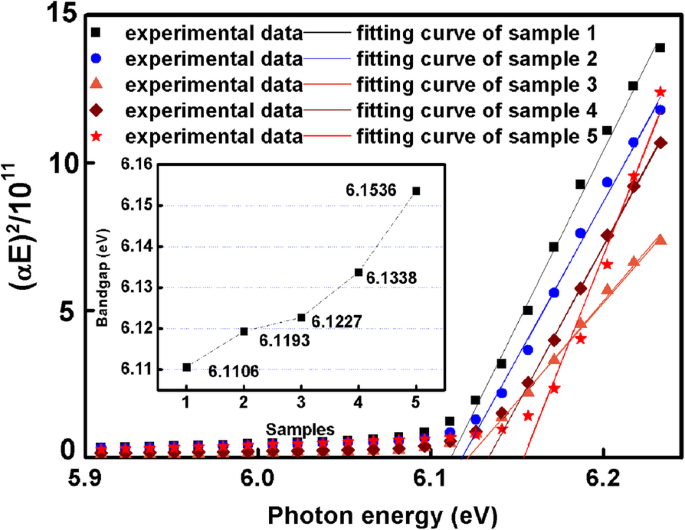
Dependência de ( αE ) ² em ( E ), a imagem inserida mostra o bandgap dos modelos AlN

onde E é a energia do fóton e E _g é o bandgap de AlN. a e b são constantes iguais a 13,70 e 7,81 para AlN, respectivamente. O índice de refração de AlN deve diminuir com o aumento de E _g de acordo com a fórmula. No entanto, neste trabalho, o índice de refração de AlN aumenta com o aumento de E _g , o que significa que a influência do bandgap no índice de refração de AlN pode ser desprezada em comparação com a influência de TDDs. Portanto, a mudança de TDDs desempenha um papel fundamental na mudança do índice de refração de AlN.

Combinado com as análises acima, é confirmado que o campo de deformação em nanoescala irá influenciar a distribuição do índice de refração em torno dos deslocamentos, que influenciam ainda mais o índice de refração de AlN. Os deslocamentos irão diminuir a refração do AlN de acordo com os dados experimentais.

Conclusões

Em conclusão, o efeito dos TDDs no índice de refração do AlN é estudado tanto experimentalmente quanto teoricamente. Evitando a influência da temperatura, estresse e bandgap, pode-se concluir que o índice de refração do AlN diminui com o aumento dos TDDs. Outros estudos mostraram que o campo de deformações em nanoescala em torno dos deslocamentos resulta no índice de refração mudando significativamente ao redor dos deslocamentos. A dispersão e a interferência ocorrerão quando a luz se propagar por meio de deslocamentos e, portanto, o índice de refração de AlN será alterado. As descobertas neste trabalho serão benéficas para otimizar dispositivos optoeletrônicos DUV baseados em AlN.

Disponibilidade de dados e materiais

Todos os dados podem ser fornecidos mediante solicitação adequada.

Abreviações

DBR:: Refletor Bragg Distribuído
DUV:: Ultravioleta profundo
EQE:: Eficiência quântica externa
FWHM:: Largura total pela metade no máximo
LEDs:: Diodos emissores de luz
LEE:: Eficiência de extrato leve
MOCVD:: Deposição de vapor químico orgânico de metal
MSE:: Erro quadrático médio
SE:: Elipsométrico espectroscópico
TDDs:: Densidades de deslocamento de rosca
XRC:: Curva de balanço XRD
XRD:: Difração de raios X

Transições de fase e formação de uma estrutura do tipo monocamada em filmes finos de oligotiofeno:exploração com uma combinação de difração de raios-X in situ e medições elétricas Sensor de pressão flexível capacitivo baseado em papel de alto desempenho e sua aplicação em medições relacionadas a humanos

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias