Exemplos de simplificação de circuitos

Vamos começar com um circuito de porta semicondutor que precisa de simplificação.

Os sinais de entrada "A", "B" e "C" são considerados fornecidos por interruptores, sensores ou talvez outros circuitos de porta.

A origem desses sinais não é uma preocupação na tarefa de redução da porta.

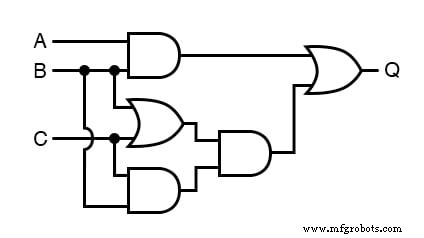
Como escrever uma expressão booleana para simplificar circuitos

Nosso primeiro passo na simplificação deve ser escrever uma expressão booleana para este circuito.

Esta tarefa é facilmente realizada passo a passo se começarmos escrevendo subexpressões na saída de cada porta, correspondendo aos respectivos sinais de entrada para cada porta.

Lembre-se de que as portas OR são equivalentes à adição booleana, enquanto as portas AND são equivalentes à multiplicação booleana.

Por exemplo, vou escrever subexpressões nas saídas das três primeiras portas:







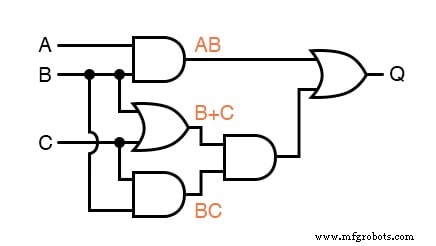
. . . em seguida, outra subexpressão para o próximo portão:







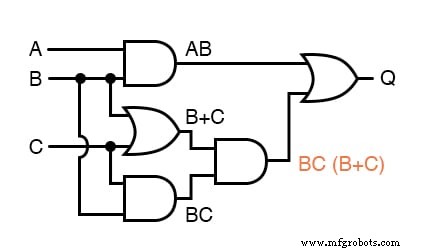
Finalmente, a saída (“Q”) é vista como igual à expressão AB + BC (B + C):







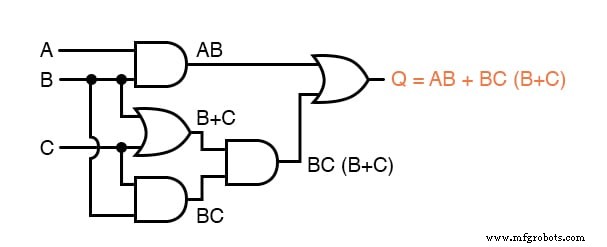
Agora que temos uma expressão booleana para trabalhar, precisamos aplicar as regras da álgebra booleana para reduzir a expressão à sua forma mais simples (a mais simples é definida como requerendo o menor número de portas para implementar):







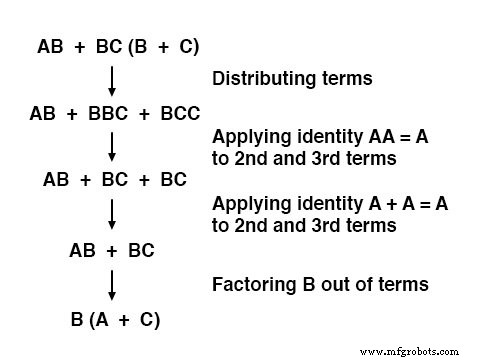
A expressão final, B (A + C), é muito mais simples do que a original, mas executa a mesma função.

Se você gostaria de verificar isso, você pode gerar uma tabela verdade para ambas as expressões e determinar o status de Q (a saída dos circuitos) para todas as oito combinações de estado lógico de A, B e C, para ambos os circuitos. As duas tabelas de verdade devem ser idênticas.

Gerando diagramas esquemáticos a partir de expressões booleanas

Agora, devemos gerar um diagrama esquemático a partir desta expressão booleana.

Para fazer isso, avalie a expressão, seguindo a ordem matemática apropriada de operações (multiplicação antes da adição, operações entre parênteses antes de qualquer outra coisa) e desenhe portas para cada etapa.

Lembre-se novamente de que as portas OR são equivalentes à adição booleana, enquanto as portas AND são equivalentes à multiplicação booleana.

Nesse caso, começaríamos com a subexpressão “A + C”, que é uma porta OR:







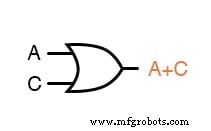
A próxima etapa na avaliação da expressão "B (A + C)" é multiplicar (porta AND) o sinal B pela saída da porta anterior (A + C):







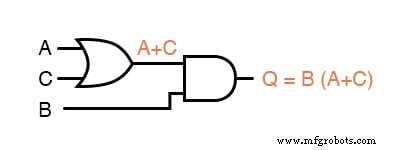
Obviamente, este circuito é muito mais simples do que o original, tendo apenas duas portas lógicas em vez de cinco.

Tal redução de componente resulta em maior velocidade operacional (menos tempo de atraso da transição do sinal de entrada para a transição do sinal de saída), menos consumo de energia, menos custo e maior confiabilidade.

Como usar a simplificação booleana para circuitos de relé eletromecânico

Os circuitos de relé eletromecânicos, normalmente mais lentos, consumindo mais energia elétrica para operar, custando mais e tendo uma vida média mais curta do que seus equivalentes semicondutores, se beneficiam dramaticamente da simplificação booleana. Vamos considerar um exemplo de circuito:







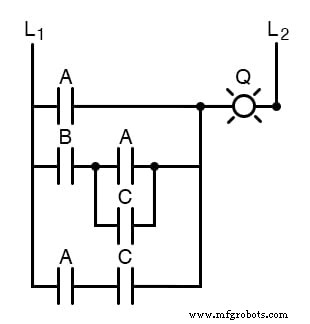
Como antes, nosso primeiro passo para reduzir este circuito à sua forma mais simples deve ser desenvolver uma expressão booleana a partir do esquema.

A maneira mais fácil que descobri de fazer isso é seguir as mesmas etapas que normalmente seguiria para reduzir uma rede de resistores em série paralela a uma única resistência total.

Por exemplo, examine a seguinte rede de resistores com seus resistores dispostos no mesmo padrão de conexão que os contatos do relé no circuito anterior e a fórmula de resistência total correspondente:







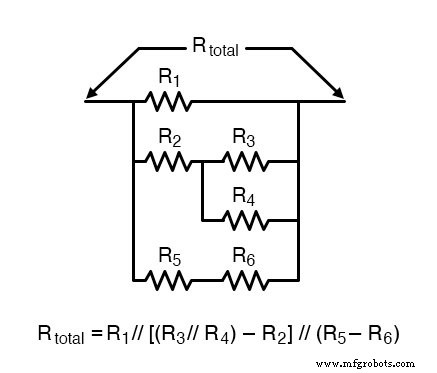
Na figura acima, um símbolo de traço longo (-) é usado para representar a conexão em série dos resistores.

Lembre-se de que os contatos paralelos são equivalentes à adição booleana, enquanto os contatos em série são equivalentes à multiplicação booleana.

Escreva uma expressão booleana para este circuito de contato do relé, seguindo a mesma ordem de precedência que você seguiria para reduzir uma rede de resistores em série-paralelo a uma resistência total.

Pode ser útil escrever uma subexpressão booleana à esquerda de cada "degrau" da escada, para ajudar a organizar sua escrita de expressão:







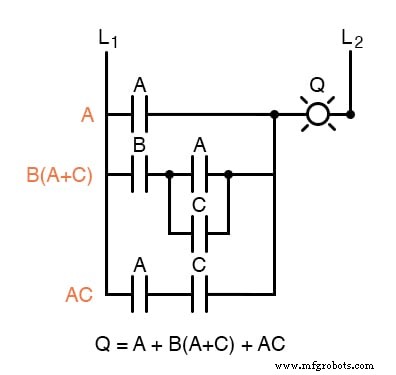
Agora que temos uma expressão booleana para trabalhar, precisamos aplicar as regras da álgebra booleana para reduzir a expressão à sua forma mais simples (a mais simples é definida como requerendo o menor número de contatos de relé para implementar):







Os mais inclinados à matemática devem ser capazes de ver que as duas etapas que empregam a regra “A + AB =A” podem ser combinadas em uma única etapa, sendo a regra expansível para:“A + AB + AC + AD +. . . =A ”







Como você pode ver, o circuito reduzido é muito mais simples do que o original, mas executa a mesma função lógica:







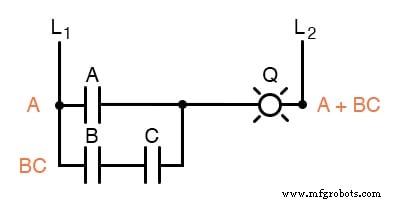
REVER:

• Para converter um circuito de porta em uma expressão booleana, rotule cada saída de porta com uma subexpressão booleana correspondente aos sinais de entrada das portas, até que uma expressão final seja alcançada na última porta.
• Para converter uma expressão booleana em um circuito de porta, avalie a expressão usando a ordem padrão de operações:multiplicação antes da adição e operações entre parênteses antes de qualquer outra coisa.
• Para converter um circuito de lógica ladder em uma expressão booleana, rotule cada linha com uma subexpressão booleana correspondente aos sinais de entrada dos contatos, até que uma expressão final seja alcançada na última bobina ou luz. Para determinar a ordem apropriada de avaliação, trate os contatos como se fossem resistores e como se você estivesse determinando a resistência total da rede série-paralela formada por eles. Em outras palavras, procure contatos que estão diretamente em série ou diretamente em paralelo um com o outro primeiro e, em seguida, “reduza”-os em subexpressões booleanas equivalentes antes de prosseguir para outros contatos.
• Para converter uma expressão booleana em um circuito de lógica ladder, avalie a expressão usando a ordem padrão de operações:multiplicação antes da adição e operações entre parênteses antes de qualquer outra coisa.

PLANILHAS RELACIONADAS:

• Planilha de expressões de soma de produtos e produto de somas
• Planilha de álgebra booleana