Simplificação da lógica com mapas de Karnaugh

Os exemplos de simplificação de lógica que fizemos até agora poderiam ter sido executados com álgebra booleana com a mesma rapidez. Os problemas de simplificação da lógica do mundo real exigem mapas de Karnaugh maiores para que possamos fazer um trabalho sério.

Trabalharemos alguns exemplos inventados nesta seção, deixando a maioria das aplicações do mundo real para o capítulo de Lógica Combinatória. Por artificial, queremos dizer exemplos que ilustram técnicas.

Essa abordagem desenvolverá as ferramentas de que precisamos para fazer a transição para as aplicações mais complexas no capítulo de Lógica Combinatória.

Mapas de Karnaugh e sequência de código Gray

Mostramos nosso mapa de Karnaugh desenvolvido anteriormente. Usaremos o formulário à direita.







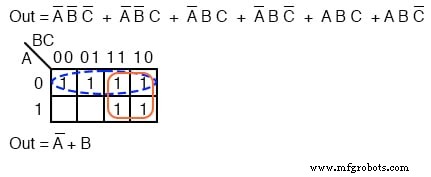
Observe a sequência de números na parte superior do mapa. Não está na sequência binária que seria 00, 01, 10, 11 . É 00, 01, 11, 10 , que é a sequência de código Gray. A sequência de código cinza muda apenas um bit binário conforme vamos de um número para o próximo na sequência, ao contrário do binário.

Isso significa que as células adjacentes variam apenas em um bit, ou variável booleana. Isso é o que precisamos para organizar as saídas de uma função lógica para que possamos ver os pontos em comum.

Além disso, os cabeçalhos das colunas e linhas devem estar na ordem do código Gray, ou o mapa não funcionará como um mapa de Karnaugh. As células que compartilham variáveis ​​booleanas comuns não seriam mais adjacentes, nem mostrariam padrões visuais.

As células adjacentes variam em apenas um bit porque uma sequência de código Gray varia em apenas um bit.

Gerando código Gray

Se esboçarmos nossos próprios mapas de Karnaugh, precisaremos gerar o código Gray para mapas de qualquer tamanho que possamos usar. É assim que geramos código Gray de qualquer tamanho.







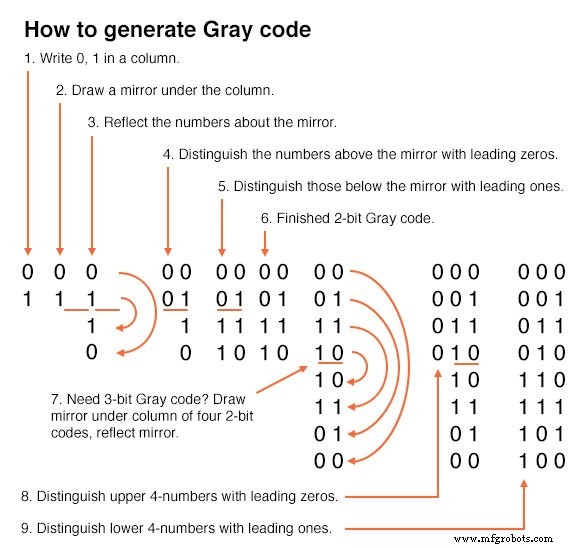
Observe que a sequência do código Gray, acima à direita, varia apenas um bit à medida que avançamos na lista, ou de baixo para cima na lista. Esta propriedade do código Gray é frequentemente útil para eletrônicos digitais em geral. Em particular, é aplicável aos mapas de Karnaugh.

Exemplos de simplificação com mapas de Karnaugh

Vamos prosseguir para alguns exemplos de simplificação com mapas de Karnaugh de 3 variáveis. Mostramos como mapear os termos do produto da lógica não simplificada para o K-map.

Ilustramos como identificar grupos de células adjacentes que levam a uma simplificação da Soma de Produtos da lógica digital.







Acima de nós, coloque os 1s no K-map para cada um dos termos do produto, identifique um grupo de dois e, em seguida, escreva um p-termo (termo do produto) para o único grupo como nosso resultado simplificado.







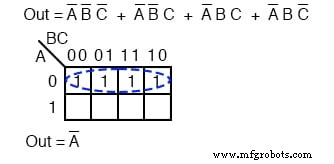
Mapear os quatro termos do produto acima resulta em um grupo de quatro cobertos pelo Booleano A ’







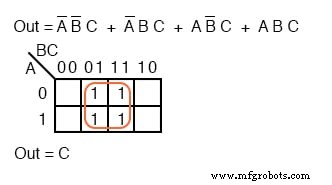
O mapeamento dos quatro p-termos produz um grupo de quatro, que é coberto por uma variável C .







Depois de mapear os seis p-termos acima, identifique o grupo superior de quatro, pegue as duas células inferiores como um grupo de quatro, compartilhando as duas com mais duas do outro grupo. Cobrir esses dois com um grupo de quatro fornece um resultado mais simples.

Como existem dois grupos, haverá dois p-termos no resultado da Soma de Produtos A ’+ B







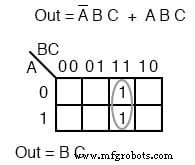
Os dois termos de produto acima formam um grupo de dois e se simplificam para BC







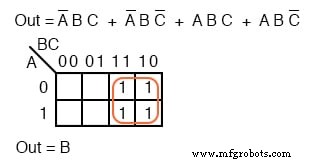
O mapeamento dos quatro p-termos produz um único grupo de quatro, que é B







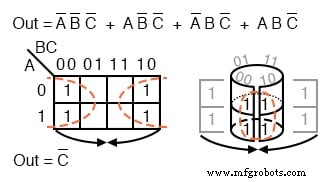
O mapeamento dos quatro p-termos acima resulta em um grupo de quatro. Visualize o grupo de quatro enrolando as extremidades do mapa para formar um cilindro, então as células são adjacentes. Normalmente marcamos o grupo de quatro como acima à esquerda.

Fora das variáveis ​​A, B, C, há uma variável comum:C '. C 'é um 0 geral de quatro células. O resultado final é C ’



.



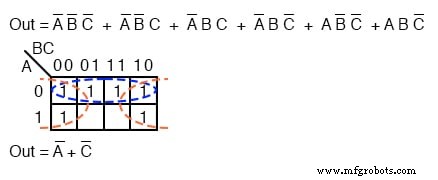
As seis células acima da equação não simplificada podem ser organizadas em dois grupos de quatro. Esses dois grupos devem nos dar dois termos-p em nosso resultado simplificado de A ’+ C’ .

Simplificando Equações Booleanas com Mapas de Karnaugh

Abaixo, revisitamos o incinerador de lixo tóxico do capítulo de álgebra booleana. Consulte o capítulo de álgebra booleana para obter detalhes sobre este exemplo. Vamos simplificar a lógica usando um mapa de Karnaugh.







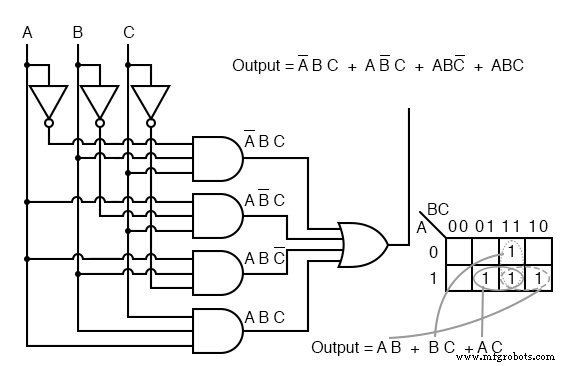
A equação booleana para a saída tem quatro termos de produto. Mapeie quatro 1's correspondentes aos p-termos. Formando grupos de células, temos três grupos de dois. Haverá três p-termos no resultado simplificado, um para cada grupo. Consulte Convertendo tabelas de verdade em expressões booleanas do capítulo 7 para um diagrama de portas do resultado, que é reproduzido abaixo.







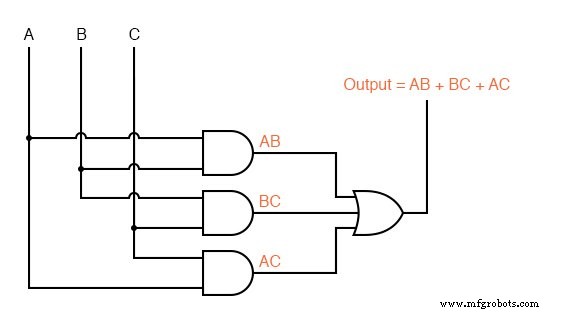
A seguir, repetimos a simplificação da álgebra booleana do incinerador de resíduos tóxicos para comparação.







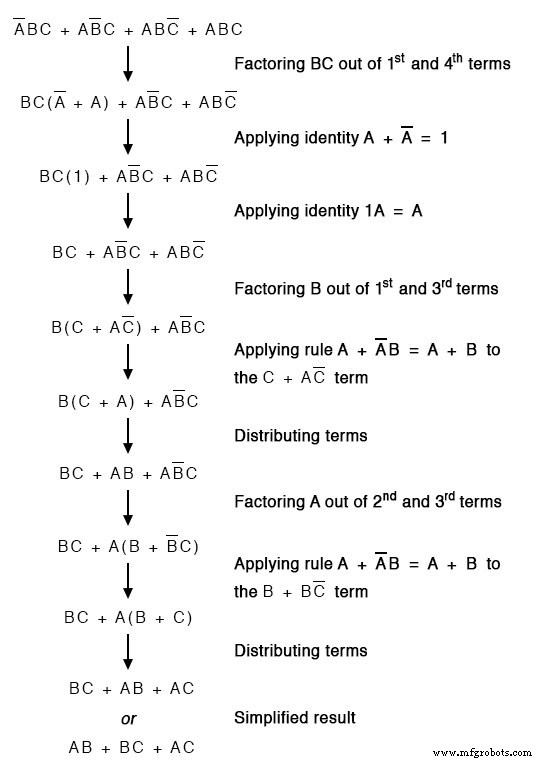
Abaixo, repetimos a solução do mapa de Karnaugh do incinerador de resíduos tóxicos para comparação com a simplificação da álgebra booleana acima. Este caso ilustra porque o mapa de Karnaugh é amplamente usado para simplificação lógica.







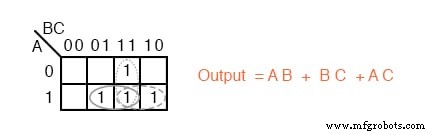
O método do mapa de Karnaugh certamente parece mais fácil do que as páginas anteriores da álgebra booleana.



PLANILHAS RELACIONADAS:

• 
  Planilha de mapeamento de Karnaugh