Alguns exemplos com circuitos CA

Vamos conectar três fontes de tensão CA em série e usar números complexos para determinar as tensões aditivas.

Todas as regras e leis aprendidas no estudo dos circuitos DC se aplicam aos circuitos AC também (Lei de Ohm, Leis de Kirchhoff, métodos de análise de rede), com exceção dos cálculos de potência (Lei de Joule).

A única qualificação é que todas as variáveis ​​ devem ser expressa de forma complexa, levando em consideração a fase e a magnitude, e todas as tensões e correntes devem ter a mesma frequência (para que suas relações de fase permaneçam constantes). (Figura abaixo)

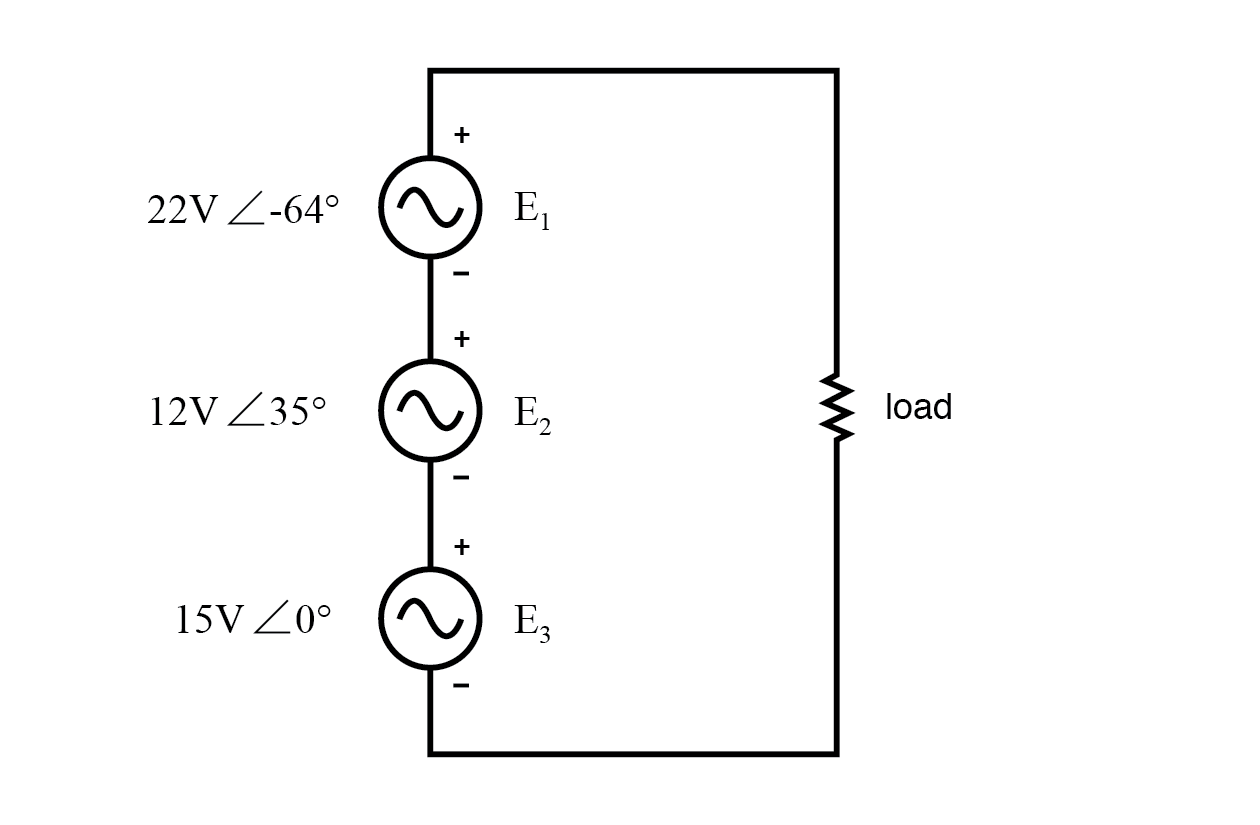
KVL permite a adição de tensões complexas.



As marcas de polaridade para todas as três fontes de tensão são orientadas de tal forma que suas tensões declaradas devem somar para formar a tensão total através do resistor de carga.

Observe que, embora a magnitude e o ângulo de fase sejam fornecidos para cada fonte de tensão CA, nenhum valor de frequência é especificado. Se for esse o caso, presume-se que todas as frequências são iguais, atendendo assim às nossas qualificações para a aplicação das regras DC a um circuito CA (todos os valores dados na forma complexa, todos com a mesma frequência).

A configuração de nossa equação para encontrar a tensão total aparece como tal:







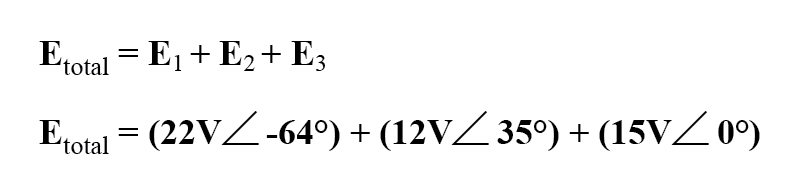
Graficamente, os vetores somam conforme mostrado na Figura abaixo.

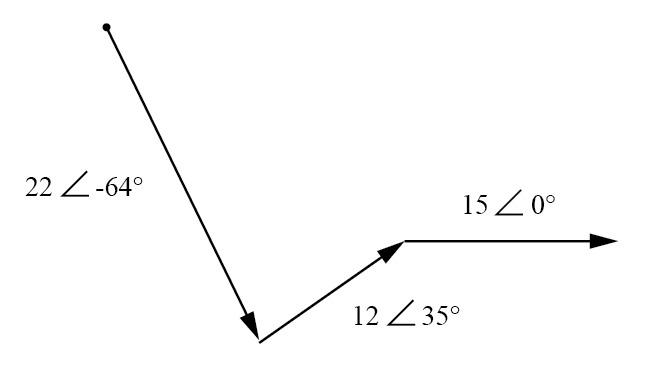
Adição gráfica de tensões de vetor.



A soma desses vetores será um vetor resultante originado no ponto inicial para o vetor de 22 volts (o ponto no canto superior esquerdo do diagrama) e terminando no ponto final para o vetor de 15 volts (ponta da seta no meio -direito do diagrama):(Figura abaixo)

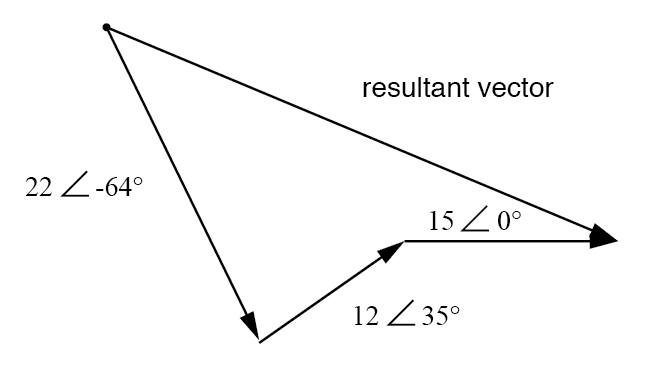
Resultante é equivalente à soma vetorial das três tensões originais.



A fim de determinar quais são a magnitude e o ângulo do vetor resultante, sem recorrer a imagens gráficas, podemos converter cada um desses números complexos de forma polar em forma retangular e adicionar.

Lembre-se, estamos adicionando essas figuras juntas porque as marcas de polaridade para as três fontes de tensão são orientadas de forma aditiva:







Na forma polar, isso equivale a 36,8052 volts ∠ -20,5018 °. O que isso significa em termos reais é que a tensão medida nessas três fontes de tensão será de 36,8052 volts, atrasando 15 volts (referência de fase 0 °) em 20,5018 °.

Um voltímetro conectado através desses pontos em um circuito real indicaria apenas a magnitude polar da tensão (36,8052 volts), não o ângulo. Um osciloscópio pode ser usado para exibir duas formas de onda de tensão e, assim, fornecer uma medição de deslocamento de fase, mas não um voltímetro.

O mesmo princípio é válido para amperímetros CA:eles indicam a magnitude polar da corrente, não o ângulo de fase.

Isso é extremamente importante para relacionar valores calculados de tensão e corrente a circuitos reais.

Embora a notação retangular seja conveniente para adição e subtração e tenha sido de fato a etapa final em nosso problema de amostra aqui, ela não é muito aplicável a medições práticas.

Figuras retangulares devem ser convertidas em figuras polares (especificamente polar magnitude ) antes que eles possam ser relacionados às medições reais do circuito.

Podemos usar SPICE para verificar a precisão de nossos resultados. Neste circuito de teste, o valor do resistor de 10 kΩ é bastante arbitrário. Está lá para que o SPICE não declare um erro de circuito aberto e aborte a análise.

Além disso, a escolha de frequências para a simulação (60 Hz) é bastante arbitrária, porque os resistores respondem uniformemente para todas as frequências de tensão e corrente CA. Existem outros componentes (principalmente capacitores e indutores) que não respondem uniformemente a diferentes frequências, mas esse é outro assunto! (Figura abaixo)

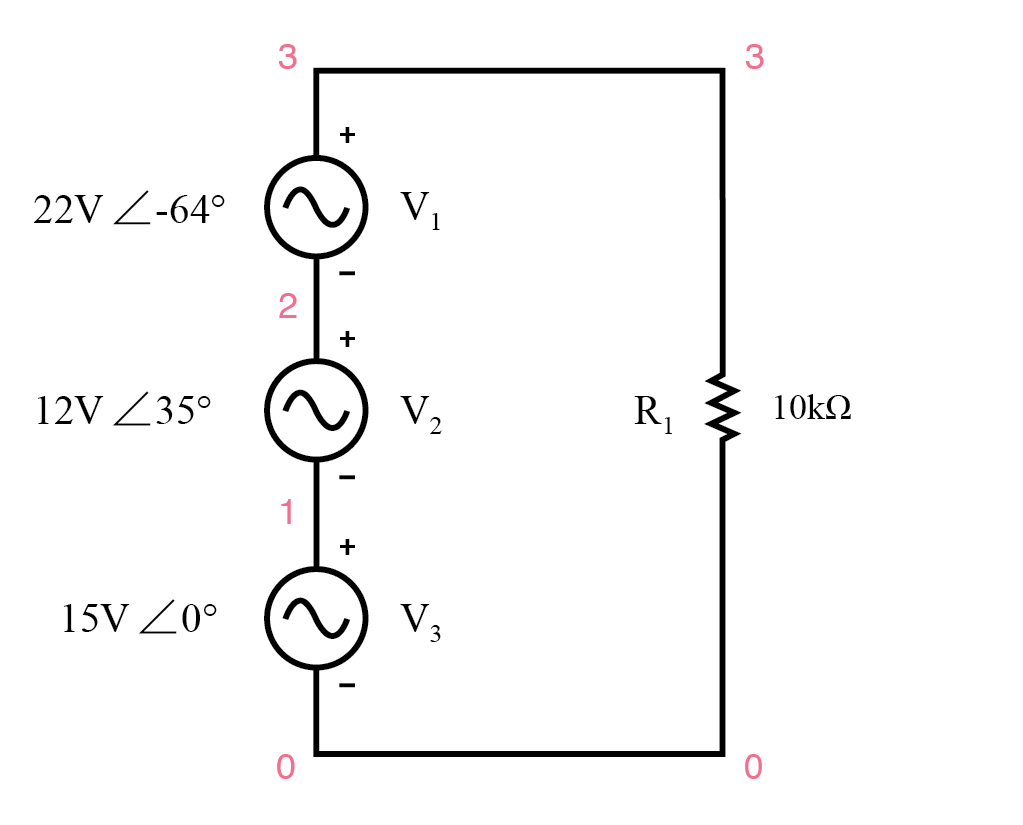
Esquema do circuito Spice.

 v1 1 0 ac 15 0 sin v2 2 1 ac 12 35 sin v3 3 2 ac 22 -64 sin r1 3 0 10k .ac link 1 60 60 Estou usando uma frequência de 60 Hz .print ac v (3,0) vp (3,0) como um valor padrão .fim freq v (3) vp (3) 6,000E + 01 3,681E + 01 -2,050E + 01 

Com certeza, obtemos uma tensão total de 36,81 volts ∠ -20,5 ° (com referência à fonte de 15 volts, cujo ângulo de fase foi arbitrariamente determinado em zero graus para ser a forma de onda de “referência”).

À primeira vista, isso é contra-intuitivo. Como é possível obter uma tensão total de pouco mais de 36 volts com fontes de 15 volts, 12 volts e 22 volts conectadas em série? Com DC, isso seria impossível, já que os valores de tensão serão somados ou subtraídos diretamente, dependendo da polaridade.

Mas com AC, nossa “polaridade” (mudança de fase) pode variar em qualquer lugar entre auxílio total e oposição total, e isso permite essa soma paradoxal.

E se pegássemos o mesmo circuito e invertêssemos uma das conexões de alimentação? Sua contribuição para a tensão total seria então o oposto do que era antes:(Figura abaixo)

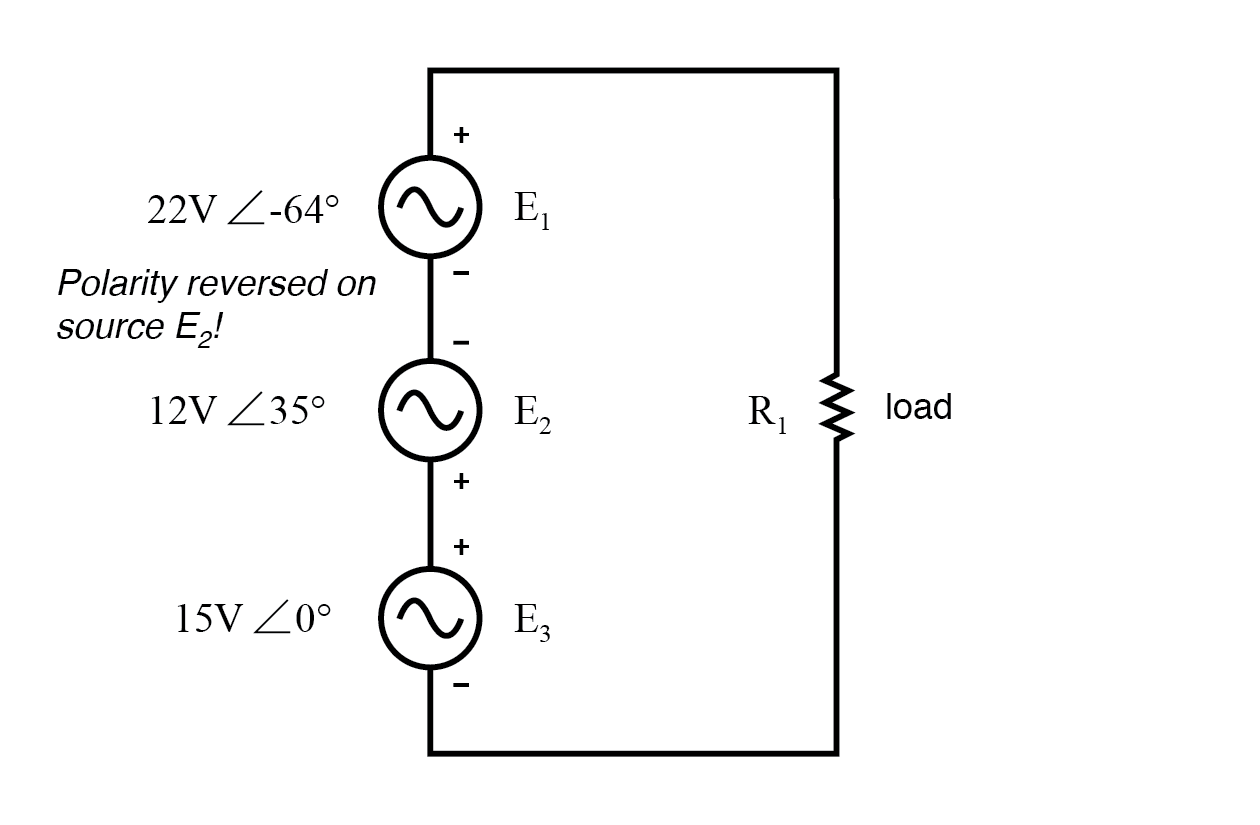
A polaridade de E ₂ (12V) está invertido.



Observe como o ângulo de fase da fonte de 12 volts ainda é referido como 35 °, embora os terminais tenham sido invertidos. Lembre-se de que o ângulo de fase de qualquer queda de tensão é determinado em referência à polaridade observada. Mesmo que o ângulo ainda esteja escrito como 35 °, o vetor será desenhado 180 ° oposto ao que era antes:(Figura abaixo)

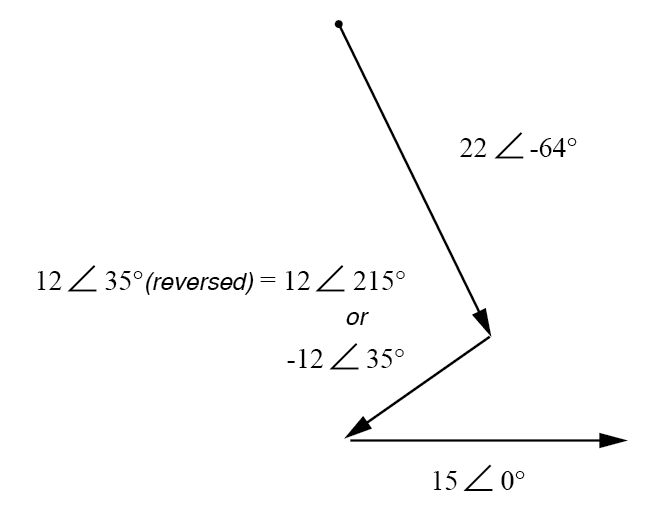
A direção de E ₂ é revertido.



O vetor resultante (soma) deve começar no ponto superior esquerdo (origem do vetor de 22 volts) e terminar na ponta da seta direita do vetor de 15 volts:(Figura abaixo)

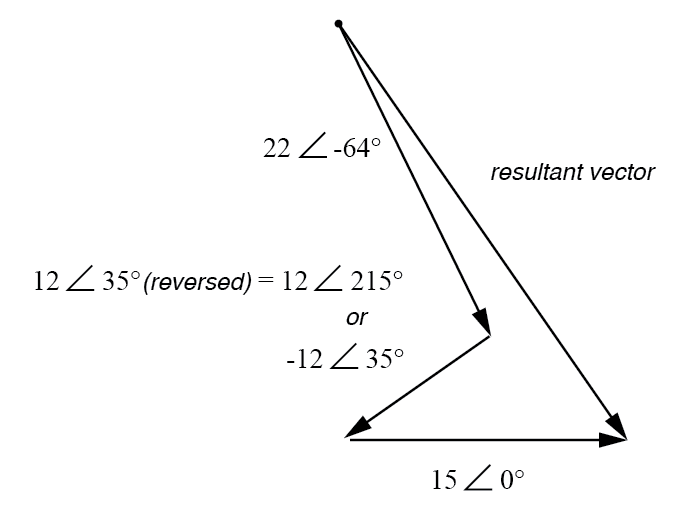
Resultante é a soma vetorial das fontes de tensão.



A reversão da conexão na fonte de 12 volts pode ser representada de duas maneiras diferentes na forma polar:pela adição de 180 ° ao seu ângulo vetorial (tornando-o 12 volts ∠ 215 °), ou uma reversão do sinal na magnitude (tornando-o - 12 volts ∠ 35 °). De qualquer forma, a conversão para a forma retangular produz o mesmo resultado:







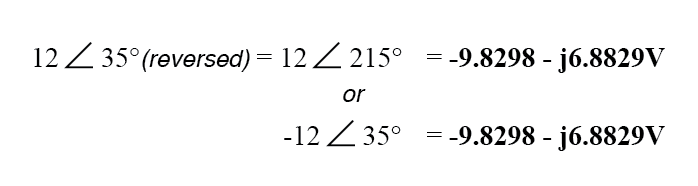
A adição resultante de tensões na forma retangular, então:







Na forma polar, isso equivale a 30,4964 V ∠ -60,9368 °. Mais uma vez, usaremos SPICE para verificar os resultados de nossos cálculos:


adição de tensão

 ac v1 1 0 ac 15 0 sin v2 1 2 ac 12 35 sin Observe a inversão dos números de nó 2 e 1 v3 3 2 ac 22 -64 sen para simular a troca de conexões r1 3 0 10k .ac lin 1 60 60 .print ac v (3,0) vp (3,0) .fim freq v (3) vp (3) 6,000E + 01 3,050E + 01 -6,094E + 01 

REVER:

• Todas as leis e regras dos circuitos DC se aplicam aos circuitos AC, com exceção dos cálculos de potência (Lei de Joule), desde que todos os valores sejam expressos e manipulados de forma complexa e todas as tensões e correntes estejam na mesma frequência .
• Ao inverter a direção de um vetor (equivalente a inverter a polaridade de uma fonte de tensão CA em relação a outras fontes de tensão), ele pode ser expresso de duas maneiras diferentes:adicionando 180 ° ao ângulo ou invertendo o sinal da magnitude.
• As medições do medidor em um circuito CA correspondem às magnitudes polares de valores calculados. Expressões retangulares de quantidades complexas em um circuito CA não têm equivalente empírico direto, embora sejam convenientes para realizar adição e subtração, conforme as leis de tensão e corrente de Kirchhoff exigem.

PLANILHAS RELACIONADAS:

• Planilha de análise de rede AC
• Planilha de leis de Kirchoff
• Planilha de leis de Ohm