Circuitos indutores de resistor da série

Na seção anterior, exploramos o que aconteceria em circuitos CA simples apenas com resistor e apenas indutor. Agora vamos misturar os dois componentes em série e investigar os efeitos.

Exemplo de circuito indutor de resistor série

Tome este circuito como um exemplo para trabalhar com:

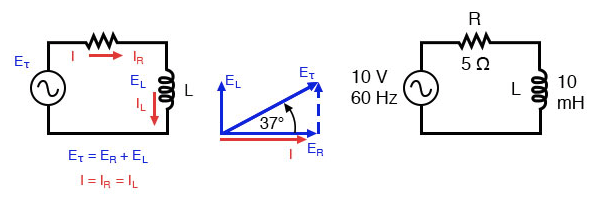
Circuito indutor de resistor em série:a tensão aplicada com defasagem de corrente de 0o a 90o.

O resistor oferecerá 5 Ω de resistência para corrente CA independentemente da frequência, enquanto o indutor oferecerá 3,7699 Ω de reatância para corrente CA em 60 Hz.

Como a resistência do resistor é um número real (5 Ω ∠ 0 °, ou 5 + j0 Ω), e a reatância do indutor é um número imaginário (3,7699 Ω ∠ 90 ° ou 0 + j3,7699 Ω), o efeito combinado de os dois componentes serão uma oposição à corrente igual à soma complexa dos dois números.

Essa oposição combinada será uma combinação vetorial de resistência e reatância. Para expressar essa oposição de forma sucinta, precisamos de um termo mais abrangente para oposição à corrente do que resistência ou reatância isoladamente.

Este termo é chamado de impedância , seu símbolo é Z, e também é expresso na unidade de ohms, assim como resistência e reatância. No exemplo acima, a impedância total do circuito é:

Resistência na Lei de Ohm

A impedância está relacionada à tensão e corrente, assim como você pode esperar, de uma maneira semelhante à resistência na Lei de Ohm:







Na verdade, esta é uma forma muito mais abrangente da Lei de Ohm do que o que foi ensinado na eletrônica CC (E =IR), assim como a impedância é uma expressão muito mais abrangente de oposição ao fluxo de corrente do que a resistência. Qualquer resistência e qualquer reatância, separadamente ou em combinação (série / paralelo), podem ser e devem ser representadas como uma única impedância em um circuito CA.

Para calcular a corrente no circuito acima, primeiro precisamos fornecer uma referência de ângulo de fase para a fonte de tensão, que geralmente é considerada zero. (Os ângulos de fase de impedância resistiva e indutiva são sempre 0 ° e + 90 °, respectivamente, independentemente dos ângulos de fase fornecidos para tensão ou corrente).







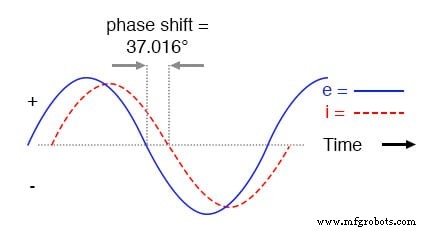
Tal como acontece com o circuito puramente indutivo, a onda de corrente fica atrás da onda de tensão (da fonte), embora desta vez o atraso não seja tão grande:apenas 37,016 ° em oposição a 90 ° completos como era o caso no circuito puramente indutivo .

A corrente atrasa a tensão em um circuito série L-R.

Para o resistor e o indutor, as relações de fase entre a tensão e a corrente não mudaram. A tensão no resistor está em fase (deslocamento de 0 °) com a corrente que passa por ele, e a tensão no indutor está + 90 ° fora de fase com a corrente que passa por ele. Podemos verificar isso matematicamente:







A tensão através do resistor tem exatamente o mesmo ângulo de fase que a corrente através dele, nos dizendo que E e I estão em fase (apenas para o resistor).







A tensão no indutor tem um ângulo de fase de 52,984 °, enquanto a corrente no indutor tem um ângulo de fase de -37,016 °, uma diferença de exatamente 90 ° entre os dois. Isso nos diz que E e I ainda estamos 90 ° defasados ​​(apenas para o indutor).

Use a Lei de Voltagem de Kirchhoff

Também podemos provar matematicamente que esses valores complexos se somam para formar a tensão total, assim como a Lei da Tensão de Kirchhoff previa:

Calcule usando SPICE

Vamos verificar a validade de nossos cálculos com SPICE:

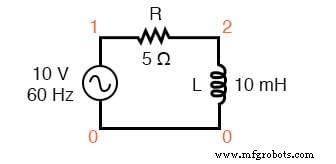
Circuito de especiarias:R-L.

 v1 1 0 ac 10 sin r1 1 2 5 l1 2 0 10m .ac lin 1 60 60 .print ac v (1,2) v (2,0) i (v1) .print ac vp (1,2) vp (2,0) ip (v1) .fim 

 freq v (1,2) v (2) i (v1) 6,000E + 01 7,985E + 00 6,020E + 00 1,597E + 00 freq vp (1,2) vp (2) ip (v1) 6,000E + 01 -3,702E + 01 5,298E + 01 1,430E + 0 

Observe que, assim como com os circuitos CC, o SPICE produz valores de corrente como se fossem negativos (180 ° fora de fase) com a tensão de alimentação. Em vez de um ângulo de fase de -37,016 °, obtemos um ângulo de fase atual de 143 ° (-37 ° + 180 °).

Isso é apenas uma idiossincrasia do SPICE e não representa nada significativo na simulação do circuito em si. Observe como as leituras de fase de tensão do resistor e do indutor correspondem aos nossos cálculos (-37,02 ° e 52,98 °, respectivamente), exatamente como esperávamos.

Com todos esses números para acompanhar, mesmo em um circuito tão simples como este, seria benéfico para nós usarmos o método da “mesa”. Aplicar uma tabela a este circuito indutor-resistor em série simples continuaria como tal.

Primeiro, faça uma tabela para os valores E / I / Z e insira todos os valores dos componentes nestes termos (em outras palavras, não insira os valores reais de resistência ou indutância em ohms e Henry, respectivamente, na tabela; em vez disso, converta-os em figuras complexas de impedância e escreva-as em):







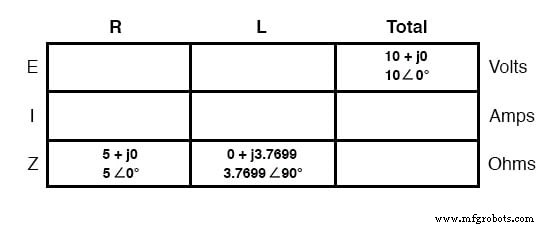
Embora não seja necessário, acho útil escrever ambos as formas retangulares e polares de cada quantidade na tabela. Se você estiver usando uma calculadora que tem a capacidade de realizar aritméticas complexas sem a necessidade de conversão entre as formas retangulares e polares, esta documentação extra é completamente desnecessária.

No entanto, se você for forçado a realizar aritméticas complexas “à mão” (adição e subtração na forma retangular e multiplicação e divisão na forma polar), escrever cada quantidade em ambas as formas será de fato útil.

Agora que nossos números “dados” estão inseridos em seus respectivos locais na tabela, podemos proceder da mesma forma que com DC:determinar a impedância total das impedâncias individuais. Como este é um circuito em série, sabemos que a oposição ao fluxo de corrente (resistência ou impedância) adiciona para formar a oposição total:







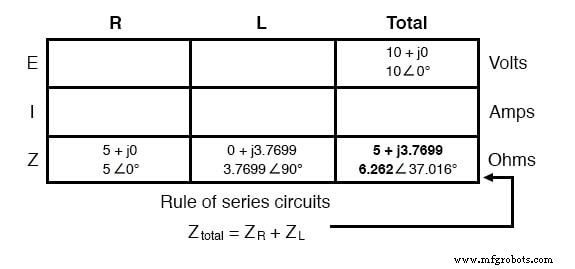
Agora que sabemos a tensão total e a impedância total, podemos aplicar a Lei de Ohm (I =E / Z) para determinar a corrente total:







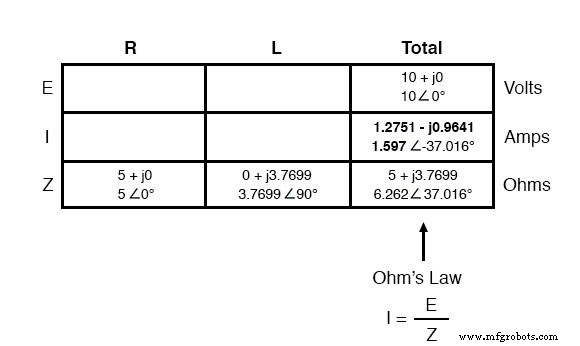
Assim como com DC, a corrente total em um circuito AC em série é compartilhada igualmente por todos os componentes. Isso ainda é verdade porque em um circuito em série há apenas um único caminho para a corrente fluir, portanto, a taxa de seu fluxo deve ser uniforme em todo. Consequentemente, podemos transferir os valores da corrente para as colunas do resistor e do indutor:







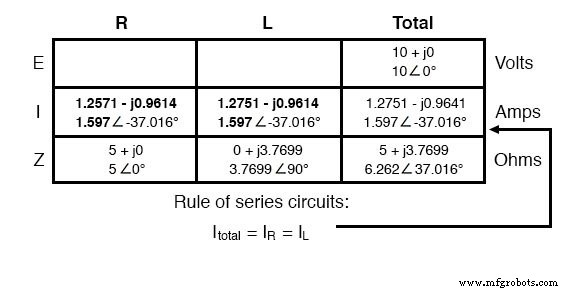
Agora tudo o que falta descobrir é a queda de tensão no resistor e no indutor, respectivamente. Isso é feito através do uso da Lei de Ohm (E =IZ), aplicada verticalmente em cada coluna da tabela:







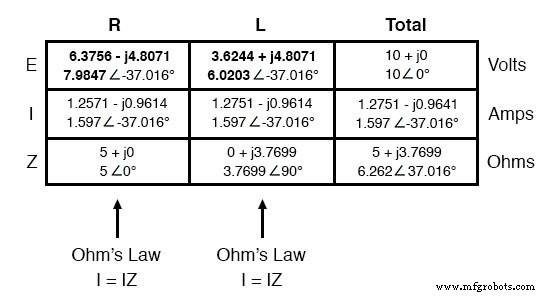
E com isso, nossa mesa está completa. As mesmas regras que aplicamos na análise de circuitos CC também se aplicam aos circuitos CA, com a ressalva de que todas as grandezas devem ser representadas e calculadas de forma complexa, em vez de escalar.

Contanto que a mudança de fase seja adequadamente representada em nossos cálculos, não há diferença fundamental em como abordamos a análise de circuito CA básica versus CC.

Agora é um bom momento para revisar a relação entre esses valores calculados e as leituras fornecidas pelas medições reais de instrumentos de tensão e corrente.

Os números aqui que se relacionam diretamente com as medições da vida real são aqueles em notação polar , não retangular! Em outras palavras, se você conectasse um voltímetro ao resistor neste circuito, ele indicaria 7,9847 volts, não 6,3756 (retangular real) ou 4,8071 (retangular imaginário) volts.

Para descrever isso em termos gráficos, os instrumentos de medição simplesmente informam quanto tempo o vetor é para aquela quantidade específica (tensão ou corrente).

A notação retangular, embora conveniente para adição e subtração aritmética, é uma forma de notação mais abstrata do que polar em relação às medições do mundo real. Como afirmei antes, indicarei as formas polares e retangulares de cada grandeza em minhas tabelas de circuito CA simplesmente por conveniência de cálculos matemáticos.

Isso não é absolutamente necessário, mas pode ser útil para aqueles que estão acompanhando sem o benefício de uma calculadora avançada. Se fôssemos nos restringir ao uso de apenas uma forma de notação, a melhor escolha seria polar, porque é a única que pode ser diretamente correlacionada com medidas reais.

A impedância (Z) de um circuito em série R-L pode ser calculada, dada a resistência (R) e a reatância indutiva (XL). Como E =IR, E =IXL e E =IZ, resistência, reatância e impedância são proporcionais à tensão, respectivamente. Assim, o diagrama fasorial de tensão pode ser substituído por um diagrama de impedância semelhante.

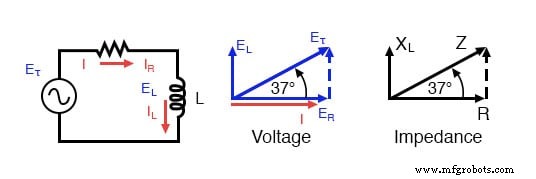
Série:diagrama fasorial da impedância do circuito R-L.



Exemplo: Dado:Um resistor de 40 Ω em série com um indutor de 79,58 millihenry. Encontre a impedância em 60 hertz.

 XL =2πfL XL =2π · 60 · 79,58 × 10-3 XL =30 Ω Z =R + jXL Z =40 + j30 | Z | =sqrt (402 + 302) =50 Ω ∠Z =arco tangente (30/40) =36,87 ° Z =40 + j30 =50∠36,87 ° 

REVER:

• Impedância é a medida total da oposição à corrente elétrica e é a soma complexa (vetorial) da resistência ("real") e da reatância ("imaginária"). É simbolizado pela letra “Z” e medido em ohms, assim como a resistência (R) e a reatância (X).
• As impedâncias (Z) são gerenciadas da mesma forma que as resistências (R) na análise de circuitos em série:as impedâncias em série são adicionadas para formar a impedância total. Apenas certifique-se de realizar todos os cálculos de forma complexa (não escalar)! Z _Total =Z ₁ + Z ₂ +. . . Z _n
• Uma impedância puramente resistiva sempre terá um ângulo de fase de exatamente 0 ° (ZR =R Ω ∠ 0 °).
• Uma impedância puramente indutiva sempre terá um ângulo de fase de exatamente + 90 ° (ZL =XL Ω ∠ 90 °).
• Lei de Ohm para circuitos AC:E =IZ; I =E / Z; Z =E / I
• Quando resistores e indutores são misturados em circuitos, a impedância total terá um ângulo de fase em algum lugar entre 0 ° e + 90 °. A corrente do circuito terá um ângulo de fase entre 0 ° e -90 °.
• Os circuitos da série CA exibem as mesmas propriedades fundamentais dos circuitos da série CC:a corrente é uniforme em todo o circuito, as quedas de tensão são adicionadas para formar a tensão total e as impedâncias são adicionadas para formar a impedância total.

PLANILHAS RELACIONADAS:

• Planilha de indutores
• Planilha de resistência, reatância e impedância
• Planilha de reatância indutiva