Regra do divisor de corrente (CDR) – Exemplos resolvidos para circuitos CA e CC
Divisão atual “CDR” para circuitos resistivos, indutivos e capacitivos
O que é a Regra do Divisor Atual (CDR)?
Quando vários elementos são conectados em paralelo, a corrente se divide em vários caminhos paralelos. E a tensão é a mesma para todos os elementos que são iguais à tensão da fonte.
Em outras palavras, quando a corrente passa por mais de um caminho paralelo (a regra do divisor de tensão “VDR” ou divisão de tensão é usada para calcular a tensão nos circuitos em série), a divisão de corrente em cada caminho. O valor da corrente que passa por um determinado ramo depende da impedância desse ramo.
A regra do divisor de corrente ou regra de divisão de corrente é a fórmula mais importante que é amplamente usada para resolver circuitos. Podemos encontrar a corrente que passa por cada ramo se conhecermos a impedância de cada ramo e a corrente total.
A corrente sempre flui pela menor impedância. Assim, a corrente tem uma relação inversa com a impedância. De acordo com a lei de ohm, a corrente que entra no nó será dividida entre eles na proporção inversa da impedância.
Isso significa que a impedância de menor valor tem uma corrente maior, pois a corrente escolheu o caminho de menor resistência. E a resistência de maior valor tem a menor corrente.
De acordo com os elementos do circuito, a regra do divisor de corrente pode descrever resistores, indutores e capacitores.
Regra do divisor de corrente para circuitos resistivos
Para entender a regra do divisor de corrente resistiva, vamos pegar um circuito no qual os resistores são conectados em paralelo. O diagrama do circuito é mostrado na figura abaixo.
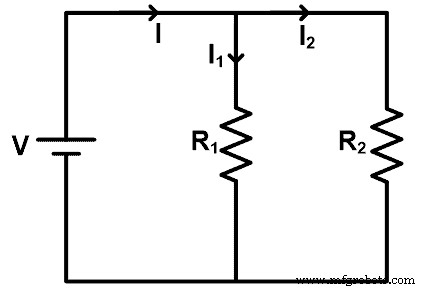
Neste exemplo, uma fonte DC alimenta todos os resistores. A tensão dos resistores é a mesma que a tensão da fonte. Mas devido à conexão paralela, a corrente se divide em diferentes caminhos. A corrente se divide em cada nó e o valor da corrente depende da resistência.
Podemos encontrar diretamente o valor da corrente que passa por cada resistor com a ajuda da regra do divisor de corrente.
Neste exemplo, a corrente principal fornecida pela fonte é I. E ela se divide em dois resistores R1 e R2 . A corrente passa pelo resistor R1 é eu1 e a corrente passa pelo resistor R2 é eu2 .
Como os resistores são conectados em paralelo. Então, a resistência equivalente é Req .
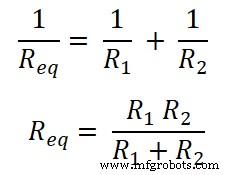
Agora, de acordo com a lei de Ohm;
V =I Req
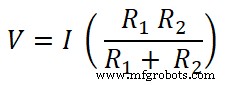
Ambos os resistores são conectados em paralelo com uma fonte DC. Portanto, a tensão através do resistor é a mesma que a tensão da fonte. E a corrente que passa pelo resistor R1 é eu1 .
Então, para o resistor R1;
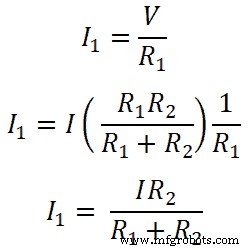
Da mesma forma, para o resistor R2;
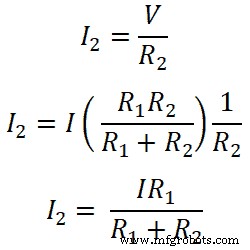
Assim, esta equação mostra uma regra divisora de corrente para resistência conectada em paralelo. A partir dessas equações, podemos dizer que a corrente que passa pelo resistor é igual à razão da multiplicação da corrente total e da resistência oposta pela resistência total.
Postagens relacionadas:
- Teorema de Thévenin. Guia passo a passo com exemplo resolvido
- Teorema de Norton. Guia passo a passo com exemplo resolvido
Regra do divisor de corrente para circuitos indutivos
Quando os indutores são conectados em paralelo, podemos aplicar a regra do divisor de corrente para encontrar a corrente que passa por cada indutor. Para entender a regra do divisor de corrente, tomamos um circuito no qual os indutores são conectados em paralelo, conforme mostrado na figura abaixo.
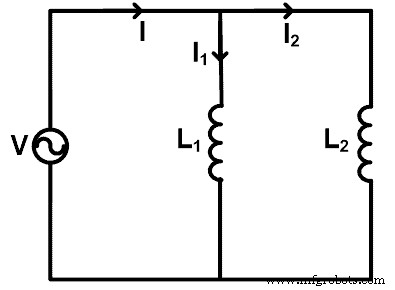
Aqui, dois indutores (L1 e L2 ) estão conectados em paralelo com uma fonte de tensão V. A corrente total que passa pela fonte é de 1 ampere. A corrente passa pelo indutor L1 é eu1 e a corrente passa pelo indutor L2 é eu2 .
Agora, precisamos encontrar as equações para a corrente I1 e eu2 . Para isso, encontraremos a indutância equivalente Leq;
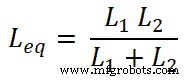
Sabemos que a corrente total que passa pelo circuito é I e é igual a;
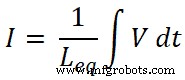
Então,
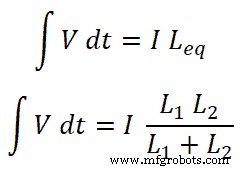
Agora, para o indutor L1 , a corrente que passa por este indutor é I1;
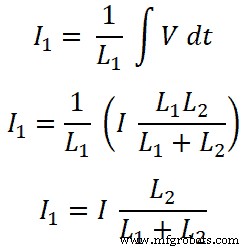
Para o indutor L2;
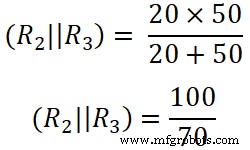
A regra do divisor de corrente para o indutor é a mesma que a regra do divisor de corrente para os resistores.
Regra do divisor de corrente para circuitos capacitivos
Quando os capacitores são conectados em paralelo, podemos encontrar a corrente que passa por cada capacitor usando a regra do divisor de corrente. Para entender a regra do divisor de corrente para o capacitor, tomamos um exemplo em que os capacitores são conectados em paralelo conforme mostrado na figura abaixo.
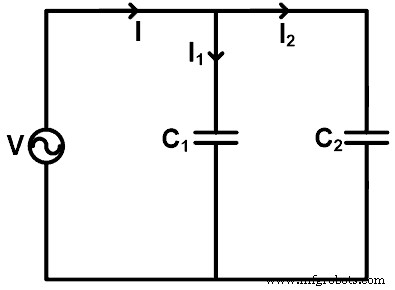
Aqui, dois capacitores (C1 e C2 ) estão conectados em paralelo com uma fonte de tensão V. A corrente passa pelo capacitor C1 é I1, e a corrente passa pelo capacitor C2 é eu2 . A corrente total fornecida pela fonte é I.
Agora, precisamos encontrar as equações para a corrente I1 e eu2 . Para isso, encontraremos a capacitância equivalente Ceq;
Ceq =C 1 + C 2
Conhecemos a equação da corrente que passa pelo capacitor. E a equação para a corrente total fornecida pela fonte é;
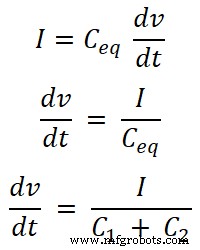
Para capacitor C1 , a corrente que passa por este capacitor é I1;
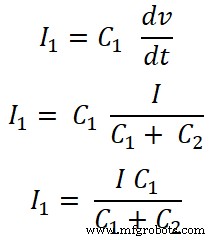
Para o capacitor C2;
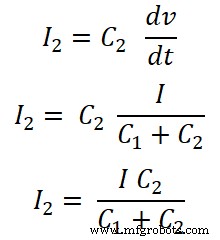
A regra do divisor de corrente para o capacitor é ligeiramente diferente da regra do divisor de corrente para o indutor e o resistor.
Na regra do divisor de corrente do capacitor, a corrente que passa por um capacitor é uma razão entre a corrente total multiplicada por aquele capacitor e a capacitância total.
Exemplos resolvidos para circuitos CA e CC usando CDR
Regra de Mergulhador Atual para Circuito DC
Exemplo:1
Encontre a corrente que passa por cada resistor pela regra do divisor de corrente para a rede fornecida.
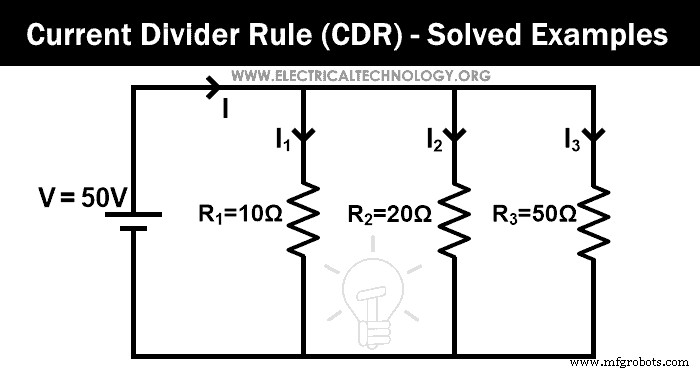
Neste exemplo, três resistores são conectados em paralelo. Primeiro, encontramos a resistência equivalente.
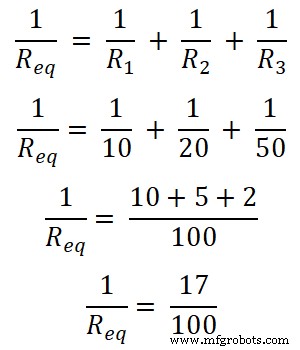
Req = 100/17
Req = 5,882Ω
A corrente total fornecida pela fonte é I. Então, de acordo com a lei de ohm;
V =I Req
50V =I (5.882Ω)
I = 50V / 5.882Ω
I = 8.5A
Agora, aplicamos a regra do divisor de corrente ao primeiro resistor (10 Ω), e a corrente que passa por esse resistor é I1;
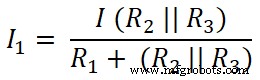
Aqui R2 e R3 estão ligados em paralelo. Então, precisamos encontrar a resistência equivalente entre R2 e R3 .
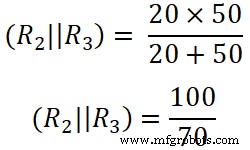
(R 2 || R 3 ) =14,285 Ω
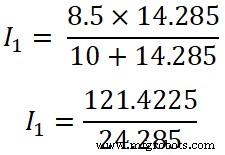
Eu 1 =4,9999 ≈ 5 A
Da mesma forma, aplicamos a regra do divisor de corrente ao Segundo resistor (20 Ω), e a corrente que passa por esse resistor é I2;
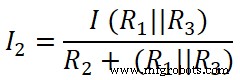
Aqui,
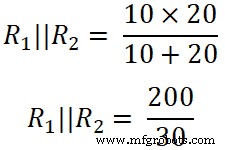
(R 1 || R 3 ) =8,33 Ω
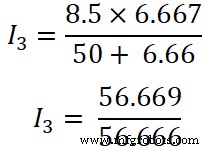
Eu 2 =2,499 ≈ 2,5 A
Agora, aplicamos a regra do divisor de corrente ao terceiro resistor (50 Ω), e a corrente que passa por esse resistor é I3 .
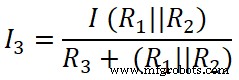
Aqui,
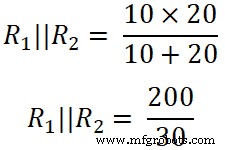
(R 1 || R 2 ) =6,66 Ω
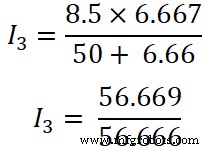
Eu 3 =1,00A
Então, a soma de todas as três correntes será;
Eu 1 + Eu 2 + Eu 3 =5 + 2,5 + 1 =8,5 A
E esta corrente é a mesma que a corrente total fornecida pela fonte.
Regra de Mergulhador Atual para Circuito CA
Exemplo-2
Considere um circuito CA com um resistor e um capacitor conectados em paralelo, conforme mostrado na figura abaixo. Encontre a corrente que passa pelo resistor e pelo capacitor usando a regra do divisor de corrente. Considere a frequência de 60 Hz.
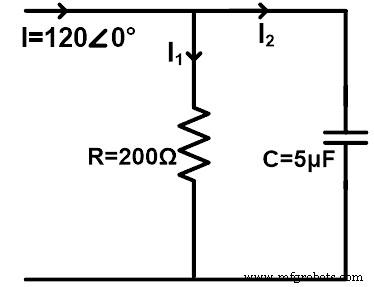
ZR =200 Ω =200∠0°Ω
ZC =1/(2 πf C) =1/(2 π 60(5×10
6
) )
ZC =10
6
/ (600 π)
ZC =530,78 ∠-90° Ω
Agora, de acordo com a regra do divisor de corrente, a equação da corrente que passa pelo resistor é;
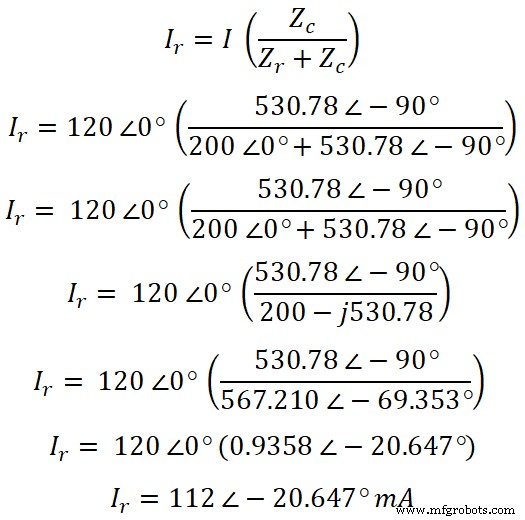
Agora, da mesma forma, podemos encontrar a corrente que passa pelo capacitor. De acordo com a regra do divisor de corrente, a equação da corrente que passa pelo capacitor é;
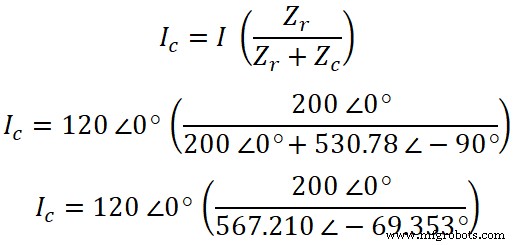
IC =120 ∠0° (0,3526 ∠ 69,353°)
IC =42,31 ∠ 69,353°
Se você quiser provar essa resposta, você pode adicionar ambas as correntes. E o valor desta corrente é o mesmo que a corrente da fonte.
Tutoriais de análise de circuitos elétricos relacionados:
- Teorema da Compensação - Demonstração, Explicação e Exemplos Resolvidos
- Teorema da Substituição – Guia Passo a Passo com Exemplo Resolvido
- Análise de circuito SUPERNODE - passo a passo com exemplo resolvido
- Análise de circuito SUPERMESH - passo a passo com exemplo resolvido
- Lei de Corrente e Tensão de Kirchhoff (KCL e KVL) | Exemplo resolvido
- Calculadora de Regras de Cramer - Sistema de 2 e 3 Equações para Circuitos Elétricos
- Ponte de Wheatstone – Circuito, Funcionamento, Derivação e Aplicações
- Calculadoras de engenharia elétrica e eletrônica
- Mais de 5.000 fórmulas e equações de engenharia elétrica e eletrônica
Tecnologia industrial



