19 Unidade 2:Eixos programáveis ​​de máquina-ferramenta CNC e sistemas de dimensionamento de posição

OBJETIVO

Após concluir esta unidade, você deverá ser capaz de:

• Entenda o sistema de coordenadas cartesianas.
• Entenda as coordenadas cartesianas do plano.
• Entenda as coordenadas cartesianas do espaço tridimensional.
• Entenda os quatro quadrantes.
• Explique a diferença entre coordenadas polares e retangulares.
• Identifique os eixos programáveis ​​em uma usinagem CNC.

O SISTEMA DE COORDENADAS CARTESIANAS

As coordenadas cartesianas permitem especificar a localização de um ponto no plano ou no espaço tridimensional. As coordenadas cartesianas ou sistema de coordenadas retangulares de um ponto são um par de números (em duas dimensões) ou um trio de números (em três dimensões) que especificam distâncias sinalizadas do eixo de coordenadas. Primeiro devemos entender um sistema de coordenadas para definir nossas direções e posição relativa. Um sistema usado para definir pontos no espaço estabelecendo direções (eixo) e uma posição de referência (origem). Um sistema de coordenadas pode ser retangular ou polar.

Assim como os pontos na linha podem ser colocados em correspondência de um para um com a linha de número real, os pontos no plano podem ser colocados em correspondência de um para um com pares de linha de número real usando duas linhas de coordenadas. Para fazer isso, construímos duas linhas de coordenadas perpendiculares que se cruzam em suas origens; Por conveniência. Atribua um conjunto de graduações de espaço igual aos eixos xey começando na origem e indo em ambas as direções, esquerda e direita (eixo x) e pontos para cima e para baixo (eixo y) ao longo de cada eixo. Fazemos uma das retas numéricas vertical com sua direção positiva para cima e direção negativa para baixo. As outras linhas numéricas horizontais com sua direção positiva para a direita e direção negativa para a esquerda. As duas linhas numéricas são chamadas de eixos de coordenadas; a linha horizontal é o eixo x, a linha vertical é o eixo y e os eixos coordenados juntos formam o sistema de coordenadas cartesianas ou um sistema de coordenadas retangulares. O ponto de intersecção dos eixos de coordenadas é denotado por O e é a origem do sistema de coordenadas. Veja a Figura 1.

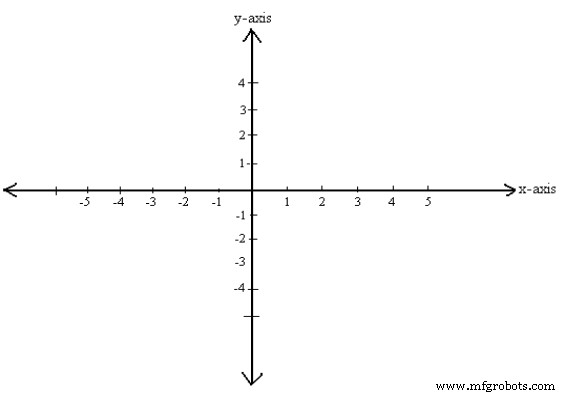
Figura 1

É basicamente, duas linhas de números reais juntas, uma indo da esquerda para a direita e a outra indo de cima para baixo. A linha horizontal é chamada de eixo x e a linha vertical é chamada de eixo y.

A Origem

O ponto (0,0) recebe o nome especial “A Origem” e às vezes recebe a letra “O”.

Linha de número real

A base deste sistema é a reta numérica real marcada em intervalos iguais. O eixo é rotulado (X, Y ou Z). Um ponto na linha é designado como Origem. Os números de um lado da linha são marcados como positivos e os do outro lado são marcados como negativos. Veja a Figura 2.

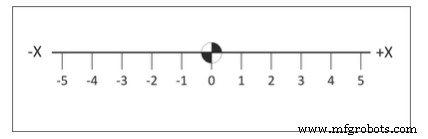
Figura 2. Linha numérica do eixo X

Coordenadas cartesianas do plano

Um plano no qual um sistema de coordenadas retangular foi introduzido é um plano de coordenadas ou um plano x-y. Mostraremos agora como estabelecer uma correspondência de um para um entre pontos em um plano coordenado e pares de números reais. Se A é um ponto em um plano coordenado, então traçamos duas linhas através de A, uma perpendicular ao eixo x e outra perpendicular ao eixo y. Se a primeira linha interceptar o eixo x no ponto com a coordenada x e a segunda linha interceptar o eixo y no ponto com a coordenada y, associamos o par (x,y) ao A (consulte a Figura 2). O número a é a coordenada x ou abcissa de P e o número b é a coordenada y ou ordenada de p; dizemos que A é o ponto com coordenada (x,y) e denotamos o ponto por A(x,y). O ponto (0,0) recebe o nome especial “A Origem” e às vezes recebe a letra “O”.

Abscissa e Ordenado:

As palavras “Abscissa” e “Ordinado” são apenas os valores xandy:

• Abscissa:o valor horizontal (“x”) em um par de coordenadas:a distância do ponto.
• Ordenada:o valor vertical ("y") em um par de coordenadas:quão longe está o ponto.

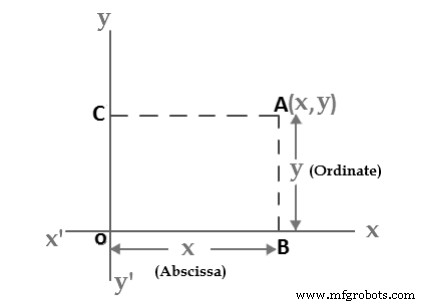
Figura 3

Valores negativos de X e Y:

A Linha de Número Real, você também pode ter valores negativos.

Negativo:comece do zero e siga na direção oposta; Veja a Figura 4

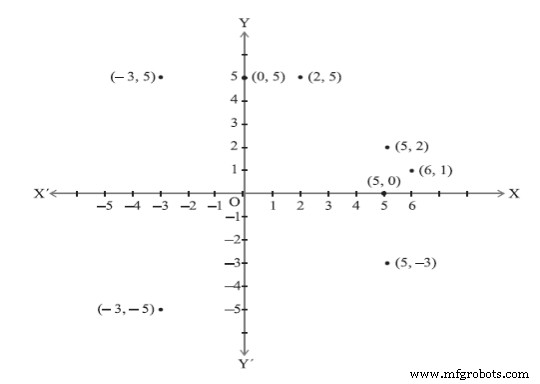
Figura 4

Então, para um número negativo:

• goleftpara x
• godownfor y

Por exemplo (-3,5)significa:
goleft ao longo do eixo x 3, em seguida, suba 5 no eixo y. (Quadrante II x é negativo, y é positivo)E(-3,-5)significa:
siga para a esquerda ao longo do eixo x 3 e depois desça 5 no eixo y. (Quadrante III x é negativo, y é negativo) Usando Coordenadas Cartesianas, marque um ponto em um gráfico pela distância e pela altura; Veja a figura 5. O ponto(12,5) é 12 unidades ao longo do eixo x e 5 unidades acima no eixo y. 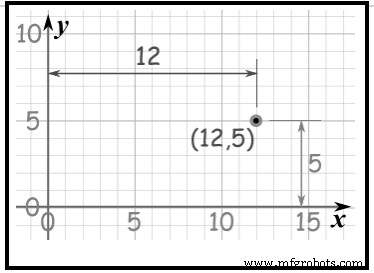Figura 5Eixos X e Y: 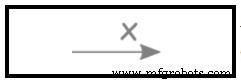A linha horizontal é chamada de eixo x e a linha vertical é chamada de eixo y; ambas as linhas passam por zero (Origem, (0,0)). A linha horizontal é chamada de eixo x e a linha vertical é chamada de eixo y; ambas as linhas passam por zero (Origem, (0,0)).Coloque-as juntas em um gráfico …Veja a figura 6

Figura 6

É basicamente, um conjunto de duas linhas de números reais.

Eixo:A linha de referência a partir da qual as distâncias são medidas.

Exemplo:
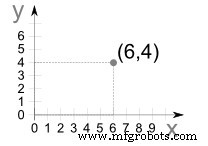Point(6,4)is
Vá ao longo da direção x 6 unidades, em seguida, suba 4 unidades na direção deles e, em seguida, "trace o ponto".

E você pode lembrar qual eixo é qual por:

As coordenadas são sempre escritas em uma certa ordem:

• a distância horizontal primeiro,
• então a distância vertical.

Par encomendado:

Os números são separados por uma vírgula e os parênteses são colocados ao redor de tudo assim:  (7,4)

Exemplo:(7,4) significa 7 unidades para a direita (eixo x) e 4 unidades para cima (eixo y)

Coordenadas cartesianas do espaço tridimensional

No espaço tridimensional (espaço xyz), orientado em ângulos retos ao plano xy. O eixo z passa pela origem do plano xy. As coordenadas são determinadas de acordo com o leste-oeste para o eixo x norte-sul para o eixo y e de cima para baixo para os deslocamentos do eixo z a partir da origem. O sistema de coordenadas cartesianas é baseado em três eixos de coordenadas mutuamente perpendiculares:o eixo x, o eixo eles e o eixo z. Consulte a Figura 6 abaixo. Os três eixos se cruzam no ponto chamado origem. Você pode imaginar a origem sendo o ponto onde as paredes no canto de uma sala encontram o chão. O eixo x é a linha horizontal ao longo da qual a parede à sua esquerda e o chão se cruzam. O eixo-eles é a linha horizontal ao longo da qual a parede à sua direita e o chão se cruzam. O eixo z é a linha vertical ao longo da qual as paredes se cruzam. As partes das linhas que você vê enquanto está na sala são a parte positiva de cada um dos eixos. A parte negativa desses eixos seriam as continuações das linhas fora da sala.

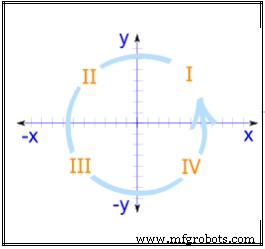
Figura 7. Sistema de coordenadas cartesianas 3D

Eixos de coordenadas cartesianas tridimensionais. Uma representação dos três eixos do sistema de coordenadas cartesianas tridimensional. O eixo x positivo, o eixo y positivo e o eixo z positivo são os lados rotulados porx,yandz. A origem é a intersecção de todos os eixos. O ramo de cada eixo no lado oposto da origem (o lado não rotulado) é a parte negativa.

Ao lidar com movimento tridimensional, é configurar um sistema de coordenadas adequado. O tipo mais direto de sistema de coordenadas é chamado de sistema cartesiano. Um sistema de coordenadas cartesianas consiste em três eixos mutuamente perpendiculares, os eixos X, Y e Z. Por convenção, a orientação desses eixos é tal que quando o dedo indicador, o dedo médio e o polegar da mão direita são configurados de modo a serem mutuamente perpendiculares, o dedo indicador, o dedo médio e o polegar podem ser alinhados ao longo dos eixos X, Y e Z, respectivamente. Tal sistema de coordenadas é denominado destro. Veja a Figura 7. O ponto de intersecção dos três eixos de coordenadas é denominado a origem do sistema de coordenadas.

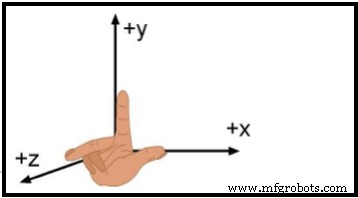
Figura 8. O sistema cartesiano destro

As coordenadas cartesianas de um ponto em três dimensões são uma trinca de números(x,y,z). Os três números, ou coordenadas, especificam a distância sinalizada da origem ao longo dos eixos x, y e z, respectivamente. Eles podem ser visualizados formando a caixa com arestas paralelas ao eixo de coordenadas e cantos opostos na origem e no ponto dado.

Os pontos podem agora ser definidos em um volume tridimensional do espaço. Isso permite definir pontos em três dimensões a partir da origem. As coordenadas cartesianas (x,y,z) de um ponto em três dimensões especificam a distância com sinal da origem ao longo dos eixos x,y, ez, respectivamente. Os pontos do eixo Z tornam-se a terceira entrada ao definir localizações de coordenadas.

Dada a analogia do canto da sala acima, poderíamos formar as coordenadas cartesianas do ponto no topo de sua cabeça, como segue. Imagine que você tem cinco metros de altura no eixo z e que caminha dois metros da origem ao longo do eixo x, depois vira à esquerda e caminha paralelamente ao eixo eles quatro metros para dentro da sala. As coordenadas cartesianas do ponto no topo de sua cabeça seriam (2,4,5).

Por exemplo, uma notação de (2,4,5) corresponde ao valor de X2, Y4 e Z5. Veja a Figura 8.

3 dimensões

As coordenadas cartesianas podem ser usadas para localizar pontos em 3 dimensões como neste exemplo:

Figura 9. O ponto (2, 4, 5 ) é mostrado em coordenadas cartesianas tridimensionais.

Quadrantes

Os eixos coordenados dividem o plano em quatro partes, chamadas de quadrantes (veja a Figura 9). Os quadrantes são numerados no sentido anti-horário, começando no canto superior direito, rotulados I, II, III e IV com designações de eixos conforme mostrado na ilustração abaixo.

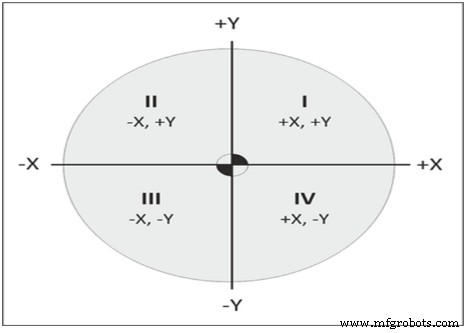
Figura 10

Quatro Quadrantes: 

Quando incluímos valores negativos, os eixos x e y dividem o espaço em 4 partes:

Quadrantes I, II, III e IV

(Eles são numerados no sentido anti-horário)

InQuadrante I:ambos x e y são positivos

InQuadrante II :x é negativo (y ainda é positivo)

No Quadrante III:ambos x e y são negativos

InQuadrant IV :x é positivo novamente, enquanto y é negativo

Quadrante	X (Horizontal)	S (Vertical)	Exemplo
Eu	Positivo	Positivo	(3,2)
II	Negativo	Positivo	(-5, 2)
III	Negativo	Negativo	(-2, -1)
IV	Positivo	Negativo	(2, -5)

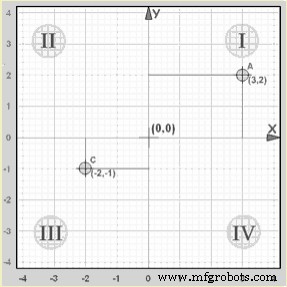
Exemplo:O ponto “A” (3,2) é 3 unidades ao longo do eixo x e 2 unidades acima do eixo y.

Ambos x e y são positivos, então esse ponto está no “Quadrante I”

Exemplo:O ponto “C” (-2,-1) é 2 unidades ao longo do eixo x na direção negativa e 1 unidade abaixo do eixo y na direção negativa.

Ambos x e y são negativos, então esse ponto está no “Quadrante III”

Dimensões:1, 2, 3 e mais…

1. A linha do número real só pode ir:

• esquerda-direita
• portanto, qualquer posição precisa de apenas um número

2. Coordenadas cartesianas podem ir:

• esquerda-direita e
• de cima para baixo
• portanto, qualquer posição precisa de dois números

3.  3 dimensões

• esquerda-direita,
• de cima para baixo e
• avançar para trás

TESTE DE UNIDADE

1. O que é CNC?

2. Descreva o sistema de coordenadas cartesianas.

3. Qual é a Origem?

4. A linha horizontal é chamada de quê?

5. A linha Vertical é chamada de quê?

6. Descreva a reta numérica real.

7. Explique Abscissa e Ordenado.

8. Quais são as representações dos três eixos do sistema de coordenadas cartesianas tridimensionais.

9. Os eixos coordenados dividem o plano em quatro partes, como se chama?

10. No Quadrante IV, os eixos X e os eixos Y são o quê?