Rotação e rotação orbital do dímero plasmônico impulsionado por luz polarizada circularmente

Resumo

O spin realçado pelo plasmon e a rotação orbital do dímero de Au, duas nanopartículas ligadas opticamente (NPs), induzidas por uma luz polarizada circularmente (CP) (onda plana ou feixe gaussiano) foram estudados teoricamente. Através dos desempenhos optomecânicos de forças e torques ópticos, o acoplamento spin-órbita longitudinal / transversal (SOC) de campos eletromagnéticos torcidos foi investigado. As forças ópticas mostram que para a interação de longo alcance, existem algumas órbitas de equilíbrio estável para rotação, onde as distâncias interpartículas de equilíbrio estável são quase múltiplos inteiros do comprimento de onda no meio. Além disso, o torque de giro óptico leva cada NP a girar individualmente. Para uma onda plana, as helicidades do spin longitudinal e rotação orbital dos NPs acoplados são as mesmas na órbita de equilíbrio estável, consistente com a lateralidade da onda plana. Em contraste, para um feixe gaussiano focalizado, a helicidade da rotação orbital do dímero poderia ser oposta à lateralidade da luz incidente devido ao torque orbital ótico negativo na distância interpartícula de equilíbrio estável; além disso, o spin transversal de cada NP torna-se profundo. Estes resultados demonstram que o SOC longitudinal / transversal é significativamente induzido devido ao campo óptico torcido. Para a interação de curto alcance, a atração mútua entre dois NPs é induzida, associada ao giro e à trajetória espiral; eventualmente, os dois NPs irão colidir. O limite da distância interpartícula entre as interações de longo e curto alcance é aproximadamente a meio comprimento de onda no meio.

Histórico

A ligação óptica de duas micropartículas (MPs) ou nanopartículas (NPs) irradiadas por uma luz polarizada linearmente (LP) é um comportamento optomecânico importante, que é o resultado da interação luz-matéria [1,2,3,4]. Existem várias distâncias interpartículas de equilíbrio estável entre o dímero ligado opticamente; essas distâncias são quase múltiplos inteiros do comprimento de onda no meio [3,4,5,6]. Além disso, a orientação do dímero é perpendicular à polarização da luz LP. Como a distância entre as partículas é próxima a múltiplos inteiros do comprimento de onda, os fótons espalhados entre as partículas fazem uma interferência construtiva para induzir uma força de ligação. Os fenômenos de arranjo opticamente ligado de MPs de sílica múltiplos ou NPs de Ag também foram estudados [7,8,9,10]. Para a iluminação de uma onda plana polarizada circularmente (CP), Haefner et al. relataram que as helicidades do spin longitudinal e rotação orbital das duas NPs de sílica acopladas com tamanho de 100-700 nm são as mesmas com a lateralidade da luz incidente [11]. Recentemente, Sule et al. experimentalmente descobriram que a helicidade da rotação orbital de dois Ag NPs de raio de 75 nm ligados pela força óptica é oposta à lateralidade de um feixe gaussiano CP focalizado de 790 nm na água [12]; isto é, dímero de Ag sofre um torque orbital óptico negativo [13, 14]. Além disso, a rotação orbital medida foi de cerca de 4 kHz [12]. Por outro lado, o spin de um único Au NP de raio 100 nm induzido por um feixe gaussiano de CP também foi estudado [15,16,17,18]. A rotação de spin medida foi tão alta quanto 3,5 kHz [15]. Nas últimas décadas, o acoplamento spin-órbita longitudinal / transversal (SOC) do campo óptico atrai muita atenção [19,20,21,22,23]. Por exemplo, um feixe de vórtice óptico (por exemplo, feixes Laguerre-Gaussianos de alta ordem com polarizações azimutais ou radiais) ou feixe gaussiano CP altamente focado pode ser usado para induzir o SOC [24,25,26,27,28,29,30 , 31,32,33,34]. O campo eletromagnético torcido (EM) do feixe de vórtice óptico carrega tanto o momento angular de spin quanto o momento angular orbital, induzindo assim o spin longitudinal / transversal e a rotação orbital de um NP de sondagem próximo [18,19,20,21,22,23 , 24,25,26]. Em particular, o SOC no campo próximo de NPs Au ou Ag é mais significativo devido ao movimento coletivo de elétrons livres nesses NPs (efeito plasmon) [28,29,30,31].

Neste artigo, estudamos teoricamente os comportamentos optomecânicos (forças ópticas e torques) de dois NPs Au acoplados (dímero) suportados por um substrato, os quais são induzidos pela iluminação de um feixe gaussiano de CP. O substrato é necessário para confinar esses NPs independentes movendo-se no plano focal, em vez de flutuar no espaço 3D. O método multipolo múltiplo (MMP) é usado para simular o campo EM numericamente e então analisar o orbital óptico e os torques de spin sobre o dímero ligado opticamente [35, 36]. Através das respostas optomecânicas do dímero, o SOC longitudinal / transversal será manifestado. Em particular, a condição para gerar um torque orbital óptico negativo no dímero também será investigada.

Métodos

A Figura 1 mostra a configuração de um par de Au NPs idênticos suportados por um substrato e irradiados por uma luz CP canhota (LH) normalmente incidente (onda plana ou feixe gaussiano), onde d representa a distância entre as partículas. A cintura do feixe gaussiano é denotada por w ₀ , e o plano focal está na seção transversal central de Au NPs. As formulações do campo elétrico da onda plana e do feixe gaussiano são anexadas como apêndice. Assumimos que o índice de refração do substrato é o mesmo do meio circundante, a água. Portanto, a luz refletida não será induzida na interface entre o meio e o substrato; o campo óptico não é perturbado pela existência do substrato [37]. Por outro lado, a existência do substrato serve como um confinamento para suportar NPs que se movem no substrato. O método multipolar múltiplo (MMP) é usado para simular o campo eletromagnético induzido [17, 18, 35, 36]. As forças ópticas F ^j exercido sobre o j º NP ( j =1, 2) são expressos por
$$ {\ mathbf {F}} ^ j ={\ int} _ {S_j} \ mathbf {T} \ cdot \ mathbf {n} \ kern0.1em \ mathrm {d} S. $$ (1)
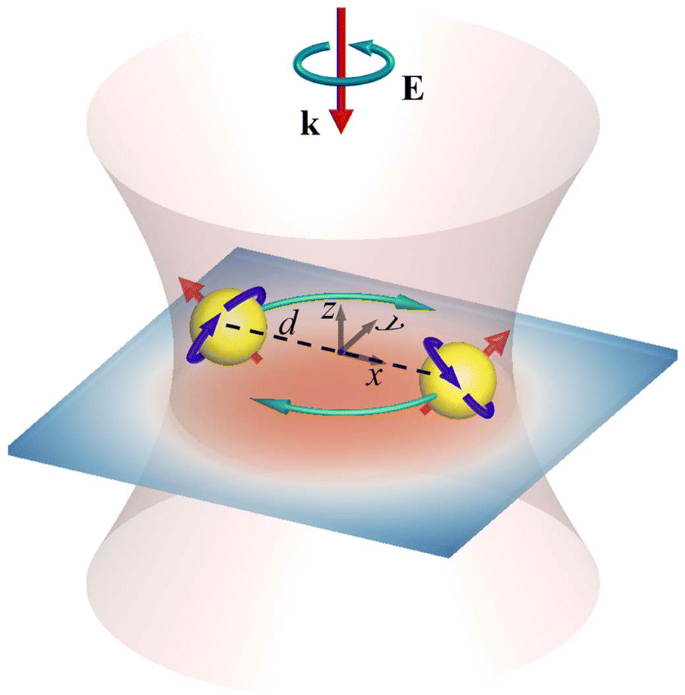
Configuração de um par de NPs com um substrato de suporte, irradiado por um feixe gaussiano LH CP normalmente incidente de cintura (w0). As seções transversais centrais desses NPs estão no plano focal do feixe gaussiano, ed é a distância entre os centros dos NPs. As respostas optomecânicas são a rotação orbital longitudinal e spin longitudinal / transversal

Aqui, n é o vetor normal externo na superfície do j º NP e T é o tensor de tensão de Maxwell médio de tempo expresso como
$$ \ mathbf {T} =\ frac {1} {2} \ operatorname {Re} \ left \ {\ varepsilon \ mathbf {E} \ overline {\ mathbf {E}} + \ mu \ mathbf {H} \ overline {\ mathbf {H}} - \ frac {1} {2} \ left (\ varepsilon \ mathbf {E} \ cdot \ overline {\ mathbf {E}} + \ mu \ mathbf {H} \ cdot \ overline {\ mathbf {H}} \ right) \; \ mathbf {I} \ right \}. $$ (2)
Na Eq. (2), I é uma matriz de identidade 3 × 3, a barra superior denota o conjugado complexo e Re a parte real [17, 18, 35, 36]. Aqui, ε e μ são a permissividade e permeabilidade do meio circundante. Observe que o E e H são o campo total externo usado para a Eq. (2) Na verdade, T é também o fluxo de momento linear com média de tempo. Ao longo deste artigo, as forças ópticas são expressas nas coordenadas cilíndricas:radial, azimutal e z - componentes do eixo. A força radial pode dizer a atração ou repulsão entre os dois NPs e a força azimutal a helicidade da revolução orbital dos NPs.

Por outro lado, o torque óptico de rotação no j º NP ( j =1, 2) para a rotação de NP individual é dado por,
$$ {\ mathbf {M}} ^ j ={\ int} _ {S_j} {\ mathbf {x}} ^ j \ times \ mathbf {T} \ cdot \ mathbf {n} \; \ mathrm {d} S. $$ (3)
Na Eq. (3), x ^j × T é o fluxo de momento angular e x ^j é o vetor de posição relativa de um ponto x na superfície S _j em relação ao centro de massa \ ({\ mathbf {x}} _ c ^ j \) de j th NP; \ ({\ mathbf {x}} ^ j =\ mathbf {x} - {\ mathbf {x}} _ c ^ j \). A direção longitudinal é designada para ser paralela ao eixo óptico (digamos z direção) da luz incidente e a direção transversal é perpendicular ao eixo óptico. Por outro lado, o torque orbital óptico longitudinal no z direção em cada NP, causada pela força óptica azimutal, é definida como F _θ d / 2 nas coordenadas cilíndricas. A permissividade relativa de Au em λ =800 nm usado na simulação é (- 24,062, 1,507) [38].

Resultados e discussão

Nós estudamos as forças ópticas e torques exercidos em dois Au NPs idênticos com raios de 100 nm irradiados por uma onda plana LH CP normalmente incidente ou um feixe gaussiano focalizado no plano focal. O meio envolvente é a água. A fluência da onda plana ou feixe gaussiano no centro é 25 MW / cm ² . Os centros dos dois NPs independentes, suportados por um substrato virtual, podem se mover no xy plano (plano focal). As forças ópticas ( F _r , F _θ ) versus a distância interpartícula d para uma onda plana CP ou um feixe gaussiano focalizado com uma cintura de 500 nm de λ =800 nm são mostrados na Fig. 2a, b, respectivamente. A seção transversal central desses NPs está no plano focal do feixe gaussiano. A Figura 2a indica que, para uma onda plana, existem várias distâncias interpartículas de equilíbrio estável com F _r =0 e uma inclinação negativa; o primeiro d ₁ está a 603 nm e o segundo d ₂ a 1204 nm. Essas distâncias interpartículas de “equilíbrio estável” são quase múltiplos inteiros do comprimento de onda no meio; ou seja, d _m = mλ / n , onde n é o índice de refração do meio e m =1, 2, 3 ... É o resultado da interação de luz-matéria de longo alcance causada pela força de ligação óptica. Isso sugere que há uma mola óptica conectando os dois NPs; a força restauradora F _r da mola óptica mantém NPs separados uns dos outros nessas distâncias interpartículas de equilíbrio estável. Para o caso do feixe gaussiano, as duas primeiras distâncias interpartículas de equilíbrio estável d ₁ e d ₂ são 585 e 1131 nm respectivamente, como mostrado na Fig. 2b, ligeiramente menores do que aqueles de uma onda plana devido ao gradiente de força induzida pelo feixe gaussiano.

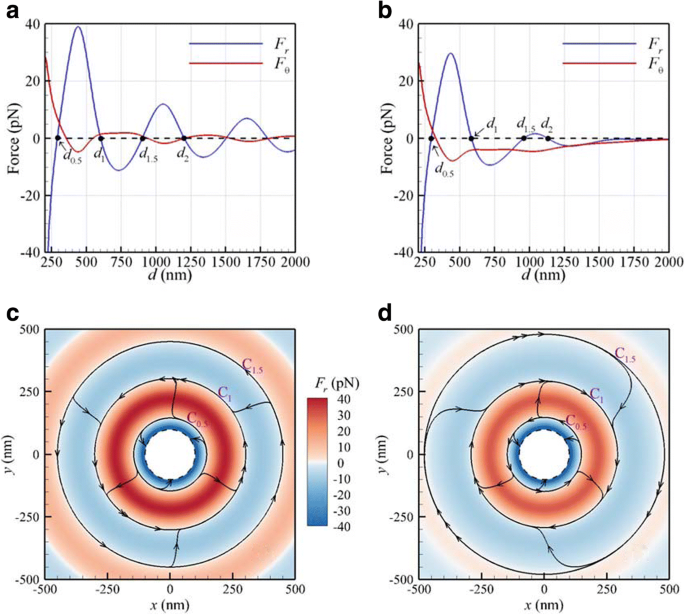
Forças ópticas ( F _r , F _θ ) versus d para λ =800 nm por CP a onda plana e b Feixe gaussiano com cintura de 500 nm no plano focal. Os mapas 2D simplificados de força óptica ( F _r , F _θ ) induzido por CP c onda plana e d Feixe gaussiano. A barra colorida representa a amplitude de F _r . O anel tracejada é o círculo limite dos centros de dois NPs onde os NPs estão em contato

Na verdade, o torque orbital longitudinal F _θ d / 2 fará com que esses NPs girem em órbitas com diâmetros de d ₁ e d ₂ . Para os casos com feixe gaussiano, as órbitas serão centralizadas no eixo do feixe. O sinal da força óptica azimutal ( F _θ ) indica que a rotação orbital longitudinal (revolução) na primeira órbita de equilíbrio estável induzida pelo feixe gaussiano é oposta àquela por uma onda plana. Isso mostra que o F negativo _θ do feixe gaussiano CP gera um torque orbital negativo F _θ d ₁ / 2 na primeira órbita de equilíbrio estável; mais importante, a helicidade da rotação orbital do dímero de Au é oposta à lateralidade da luz incidente do CP [12]. Também é interessante notar que F _θ é sempre negativo como d > 300 nm para os casos com feixe gaussiano; o fenômeno de rotação reversa (revolução) dos NPs opticamente ligados, devido ao torque orbital negativo, é facilmente observado em sistemas de pinças ópticas. O torque orbital óptico negativo pode ser atribuído ao campo EM torcido do feixe gaussiano [23].

De acordo com a lei de Stokes de uma esfera conduzida por uma força F para se mover em um fluido viscoso, a velocidade terminal v _T é v _T = F / (6 πrη ), onde η é a viscosidade dinâmica da água (0,001 kg / m s). Este é o resultado da força aplicada equilibrada por uma força de arrasto de fluido viscoso [39]. Com base na lei de Stokes, o vetor de velocidade terminal de um NP em um meio viscoso é proporcional à força aplicada [39]. Assim, usamos o campo de força óptico para obter as linhas de corrente, que são quase equivalentes às trajetórias dessas NPs. Além disso, os mapas aerodinâmicos 2D obtidos diretamente do campo de vetores de força óptica ( F _r , F _θ ) exercidos em NPs são plotados na Fig. 2c, d para onda plana e feixe gaussiano, respectivamente, onde a barra de cores representa a amplitude de F _r . Observe que a tangente da linha de fluxo em cada ponto é então paralela ao vetor de força óptica e, portanto, também é paralela à velocidade de NP. Para pequeno intervalo de distância entre as partículas ( d < d _0,5 ), a força óptica radial F _r é negativo, então esses dois NPs irão se atrair para colidir eventualmente, como mostrado na Fig. 2c, d. O anel tracejada é o círculo limite dos centros de dois NPs onde os NPs estão em contato. O anel interno (azul) é uma região da interação de curto alcance. O anel interno C _0,5 entre o anel interno (azul, com F negativo _r ) e o segundo anel (vermelho, com F positivo _r ) é a linha limite entre as regiões de interação de curto e longo alcance do dímero de Au; o diâmetro de C _0,5 é d _0,5 =291 nm na Fig. 2c e d _0,5 =296 nm na Fig. 2d. A longo prazo ( d _0,5 < d < d _1,5 ), as forças ópticas radiais e azimutais conduzem os dois NPs acoplados a se aproximar da primeira órbita de equilíbrio estável C ₁ com um diâmetro d ₁ devido ao efeito da força de ligação óptica. O dímero de Au opticamente ligado gira no sentido anti-horário (CCW) ao longo da órbita C ₁ ( d ₁ =603 nm) na Fig. 2c, enquanto ao longo de C ₁ ( d ₁ =585 nm) no sentido horário (CW) na Fig. 2d. A rotação anterior é a mesma que a destreza da luz incidente causada pelo torque orbital positivo ( F _θ > 0), e o último é reverso devido ao torque orbital negativo ( F _θ <0). De acordo com nossa análise do espectro de seção transversal de espalhamento de um dímero com uma distância de equilíbrio estável de 603 nm irradiado por uma onda plana CP (não mostrado aqui), a ressonância de plasmon de superfície de acoplamento (SPR) do dímero ligado opticamente está quase em 800 nm correspondendo à luz incidente, que é fora da ressonância de um único NP (530 nm). Em geral, o SPR de acoplamento de um dímero depende da distância entre as partículas; quanto maior a distância, mais desviado para o vermelho o SPR de acoplamento do dímero. Se usarmos um feixe gaussiano de comprimento de onda mais longo (por exemplo, 1064 nm), a distância interpartículas de equilíbrio estável aumenta. No entanto, conforme a distância entre os dois NPs se torna muito grande, o efeito de acoplamento óptico diminui, de forma que o SPR de acoplamento desaparece gradualmente. Consequentemente, o SPR de um único NP em 530 nm torna-se dominante.

Para um Au NP de raio de 100 nm que se move ao longo de uma órbita com um diâmetro d e uma velocidade angular Ω _z , a velocidade é Ω _z d / 2 = F _θ / ( 6πrμ ) Se o feixe gaussiano for aplicado ( F _θ =- 4 pN), a velocidade angular Ω _z (ciclos por segundo) ao longo de C ₁ é cerca de - 7 kHz. A ordem de magnitude é consistente com o resultado experimental [12]; a velocidade angular da rotação orbital de dois Ag NPs de r =75 nm irradiado pelo feixe gaussiano com 14 mW é - 4 kHz. Se d _1,5 < d < d _2,5 , esses NPs irão se aproximar e girar ao longo da órbita de equilíbrio estável secundária C ₂ (não mostrado aqui). Observe que, para esses casos, a força óptica de F _z é negativo para empurrar esses NPs a jusante devido à pressão de radiação; F _z =- 161,3 pN para onda plana e - 117,2 pN para o feixe gaussiano. Isso infere que a força de reação do substrato de suporte é necessária para equilibrar a força óptica motriz de F _z . Consequentemente, as forças resultantes em z a direção sobre esses NPs é zero; esses dois NPs estão confinados a se mover no xy plano do plano focal.

Por outro lado, a Fig. 3a, b mostra os torques ópticos de rotação ( M _r , M _θ , M _z ) versus d induzido por uma onda plana e feixe gaussiano no plano focal, respectivamente. Uma vez que os resultados desses dois NPs são os mesmos, apenas um conjunto de torques de rotação ópticos é plotado aqui. Os dois primeiros ( M _r , M _θ ) são os torques de rotação transversais, e os últimos M _z é o longitudinal. Verificou-se que a helicidade do torque de giro longitudinal é igual à lateralidade da luz incidente em ambos os casos. Isso ocorre porque o momento angular dos fótons absorvidos da luz CP incidente é transferido para esses NPs para rotação e rotação orbital. É interessante notar que os torques de rotação ópticos transversais ( M _r , M _θ ) induzidos por um feixe gaussiano são significativamente grandes, em comparação com os da onda plana. Isso poderia ser atribuído às componentes transversais do campo EM torcido no plano focal de um feixe gaussiano. Além disso, as magnitudes máximas dos torques de rotação transversal óptica ocorrem aproximadamente na primeira órbita de equilíbrio estável C ₁ ( d ₁ =585 nm), como mostrado na Fig. 3b. De acordo com a lei de Stokes de uma esfera giratória girada por um torque M em fluido viscoso, a velocidade angular terminal da esfera é ω _T = M / (8 πr ³ μ ) [18]. Portanto, as magnitudes das velocidades angulares de rotação longitudinal / transversal de NP em C ₁ são cerca de 10 kHz, cujas ordens de magnitude estão de acordo com a velocidade de rotação longitudinal medida [15], cerca de 3,5 kHz. Resumidamente, os fenômenos acima, conforme mostrado nas Figs. 2b e 3b, demonstram que a rotação orbital longitudinal é acompanhada pelos spins longitudinais / transversais. O movimento dos dois NPs acoplados é semelhante ao de um sistema de estrela binária, onde as forças ópticas fornecem a ligação e as forças motrizes orbitais para esses NPs, bem como os torques de spin ópticos causam seu giro.

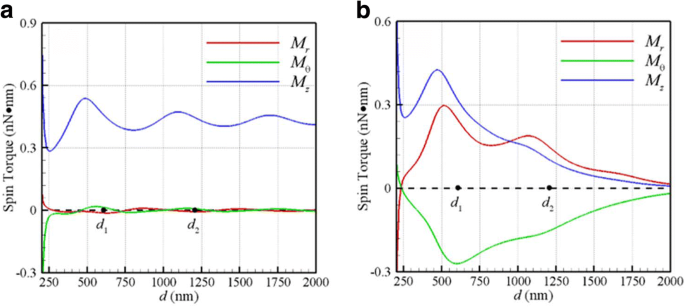
Torques de rotação óticos ( M _r , M _θ , M _z ) versus d em λ =800 nm para a onda plana e b Feixe gaussiano com w ₀ =500 nm no plano focal

Além disso, pode-se ajustar a íris do objeto de uma pinça óptica para alterar o tamanho do feixe incidente, alterando assim a abertura numérica e a cintura de um feixe gaussiano. A Figura 4a mostra o torque orbital óptico F _θ d / 2 em dois NPs Au acoplados de raio de 100 nm girando na primeira órbita de equilíbrio estável correspondente ( d = d ₁ ) versus a cintura de um feixe gaussiano CP de λ =800 nm. A primeira distância de equilíbrio estável correspondente d ₁ também é plotado na Fig. 4a (barra de escala no lado direito), onde uma onda plana pode ser tratada como um caso especial de w ₀ → ∞. O ponto de viragem para a cintura de um feixe gaussiano entre os torques orbitais positivo e negativo está em 1150 nm, correspondendo a F _θ =0, como mostrado na Fig. 4a. Quanto menor for a cintura de um feixe gaussiano, maior será a magnitude do torque orbital negativo. Conforme a cintura aumenta, o d ₁ de um feixe gaussiano se aproxima do valor (603 nm) de uma onda plana ( w ₀ → ∞). Em particular, à medida que a cintura diminui, as magnitudes dos torques de rotação transversais ( M _r , M _θ ) em d ₁ aumentar significativamente, enquanto o torque de rotação longitudinal M _z diminui, como mostrado na Fig. 4b. Esses resultados ilustram que a cintura de um feixe gaussiano é o fator chave para induzir um torque orbital longitudinal negativo e torques de rotação transversais devido ao grau de distorção do campo EM.

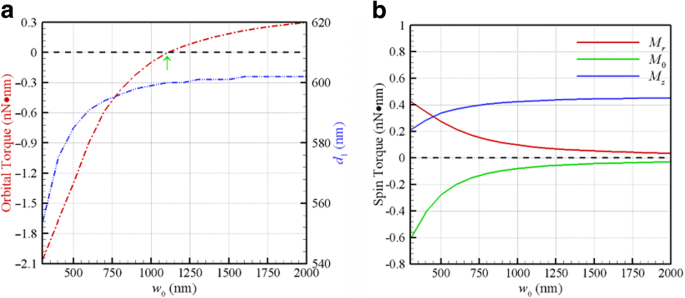
a O torque orbital óptico e d ₁ na primeira órbita de equilíbrio estável contra a cintura de um feixe gaussiano de λ =800 nm. O ponto de viragem da cintura para a produção de torque orbital positivo ou negativo é de 1150 nm. b Os torques de rotação ópticos em relação à cintura em d ₁

O mecanismo de rotação orbital negativa e o giro transversal desses NPs podem ser atribuídos pela ondulação do momento angular de rotação do campo de luz, mesmo sem a contribuição do momento angular orbital do feixe de luz [23]. Através do desempenho do torque orbital longitudinal negativo e dos torques de rotação transversal sobre o dímero de Au, o SOC de fótons aprimorado pelo plasmon pode ser manifestado. Além disso, as direções da rotação orbital do dímero e do spin do NP individual dependem da direção da luz incidente.

Conclusões

As respostas optomecânicas (forças ópticas e torques) de um par de Au NPs irradiados por luz CP foram estudadas teoricamente. Nossos resultados mostraram que as órbitas de equilíbrio estável para sua rotação (revolução) podem ser induzidas para a interação de longo alcance; as distâncias interpartículas de equilíbrio estável são quase múltiplos inteiros do comprimento de onda no meio. A força ótica azimutal causa a rotação orbital desses NPs, e o torque ótico de spin induz seu giro, principalmente os componentes transversais. Esse movimento é semelhante ao de estrelas binárias de igual massa movendo-se em uma órbita circular em torno de seu centro de massa comum. Quando a cintura de um feixe gaussiano é menor do que um ponto de viragem, a helicidade da rotação orbital do dímero de Au opticamente ligado é oposta à lateralidade da luz CP incidente. Além disso, o SOC longitudinal / transversal torna-se significativo à medida que a cintura de um feixe gaussiano diminui; portanto, o spin transversal dos dois NPs se torna mais profundo. Para a interação de curto alcance, a força óptica causa a atração mútua. Consequentemente, os dois NPs plasmônicos acoplados não apenas giram, mas também giram com uma trajetória espiral e irão colidir eventualmente. Além disso, o limite da distância interpartícula entre as interações de longo e curto alcance de duas NPs acopladas está aproximadamente a meio comprimento de onda no meio. Nossos resultados demonstraram que a ordem de magnitude da força óptica é de cerca de pN, que pode ser comparada com as outras forças (por exemplo, força ponderomotriz) para identificar a contribuição no movimento dos NPs. Nossa descoberta pode abrir caminho para as aplicações de SOC em NPs de manipulação de luz para nanociência e nanotecnologia. Além disso, vale a pena estudar a correlação entre o spin óptico e os torques orbitais nas duas NPs e as densidades de spin e momento angular orbital do campo EM; o primeiro é definido por \ (\ operatorname {Im} \ left (\ overline {\ mathbf {E}} \ times \ mathbf {E} \ right) / 2 \ omega \) e o último mostrado na Ref. [23]. Além disso, vale a pena investigar o SOC no campo próximo torcido de metamateriais [40,41,42,43].

Abreviações

CP:

Polarizado circularmente

EM:

Eletromagnética

LH:

Canhoto

LP:

Linearmente polarizado

MMP:

Multipolo múltiplo

MP:

Micropartícula

NP:

Nano-partícula

SOC:

Acoplamento spin-órbita

Transportadores de lipídios nanoestruturados híbridos liofilizados para aumentar a absorção celular de verapamil:otimização estatística e avaliação in vitro Desempenho analógico / RF do transistor de efeito de campo de túnel de fonte dupla com porta em forma de T