Algoritmo de otimização de variável ortogonal eficiente para sistemas de comunicação

Este artigo discute um algoritmo para encontrar o ponto ajustado ideal em um espaço bidimensional com vetores de entrada ortogonais. O algoritmo resolve equações para círculos que se cruzam com base em pontos de dados medidos.

Várias métricas principais de desempenho do sistema são determinadas por parâmetros de entrada ortogonais correspondentes à amplitude e fase; dois exemplos são passagem direta de portadora de modulador de quadratura e supressão de banda lateral. Esses parâmetros são aprimorados otimizando o equilíbrio de deslocamento DC e o equilíbrio de amplitude e fase entre as entradas de banda base de quadratura do modulador.

Como encontrar o ajuste ideal desses parâmetros não é uma tarefa trivial dado o espaço bidimensional, neste artigo discutirei um algoritmo Python para encontrar o ponto ajustado ideal em um espaço bidimensional com vetores de entrada ortogonais. O algoritmo resolve equações para círculos que se cruzam com base em pontos de dados medidos e encontra o ponto ideal em apenas quatro iterações. Para exemplificar a técnica, usei o conversor digital-analógico (DAC) integrado Texas Instruments (TI) AFE7070 mais o parâmetro de feedthrough da portadora do modulador de quadratura.

Otimizando Emissões Espúrias

Os sistemas de comunicação se esforçam para minimizar as emissões espúrias. Algumas dessas emissões espúrias se originam da incompatibilidade do sinal de entrada ortogonal. Por exemplo, a incompatibilidade de deslocamento DC e o desequilíbrio de amplitude / fase afetarão o feedthrough da portadora e os parâmetros de supressão de banda lateral, respectivamente, em moduladores de quadratura analógicos. Ajustar as variáveis ​​de entrada para um ponto de ajuste ideal minimiza a saída espúria.

A Figura 1 representa o parâmetro medido como a magnitude (r) do vetor do ponto otimizado, [x0, y0], até o ponto real em um plano bidimensional. O valor do parâmetro é limitado por [0,1], um círculo unitário. Um 0 representa o cancelamento completo ou nenhum sinal e um 1 representa nenhum cancelamento ou um sinal completo. Em escalas de decibéis, a função é limitada por [-inf, 0]. O círculo de raio r representa todos os pontos x, y possíveis que alcançam a mesma magnitude.

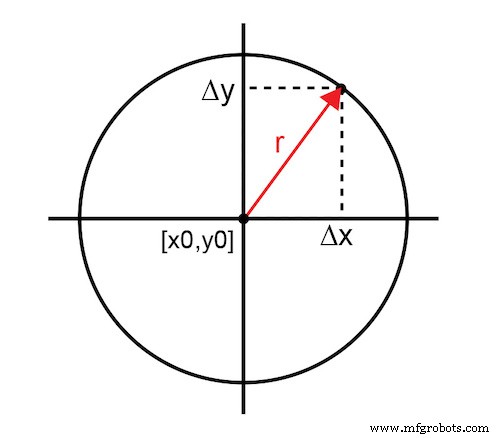
Figura 1. Vetor do ponto otimizado ao ponto real

A Equação 1 representa a função em sua forma mais simples:

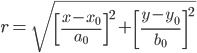(1)

Constantes [a0, b0] representam fatores de normalização dependentes do sistema para manter o resultado máximo menor que 1. Tecnicamente, a Equação 1 descreve uma elipse, pois os fatores de escala para cada variável independente não precisam ser os mesmos. Para simplificar esta análise, a0 é igual a b0 de modo que as curvas são realmente círculos.

O objetivo é encontrar o ponto ideal [x0, y0] que minimize o parâmetro de medição (r) o mais rápido possível. Encontrar esse ponto de forma eficiente com parâmetros de entrada que variam estatisticamente é um desafio. A abordagem tradicional de caça e bicada usa tentativas sucessivas para estreitar até o ponto ideal. Embora isso produza a solução desejada, são necessárias muitas iterações quando o tempo de convergência é crítico, necessitando de um novo método.

Círculos que se cruzam

Idealmente, exatamente três iterações de medição usando círculos que se cruzam determinam o ponto ideal. O primeiro resultado medido em um ponto de entrada arbitrário [x1, y1] define infinitas possibilidades para o ponto ideal representado pelo círculo A de raio r1. Adicionar um segundo ponto de dados produz outro conjunto de dados infinito representado pelo círculo B; no entanto, as interseções dos dois círculos restringem a solução a dois pontos. Um terceiro ponto de dados e o círculo C correspondente fornecem uma terceira curva onde há apenas um único ponto de interseção mútua. Esse ponto de interseção é o ponto ideal. A Figura 2 mostra a progressão dos círculos que se cruzam que culminam no ponto ótimo definitivo.

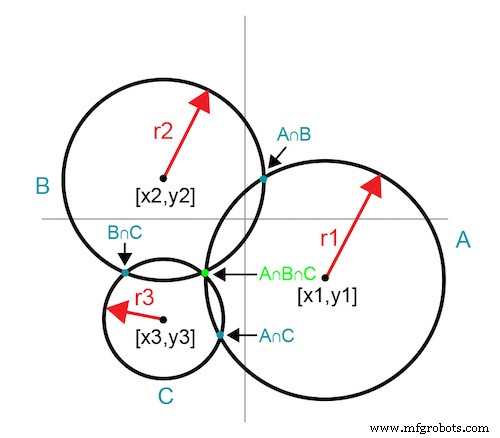
Figura 2. Círculos que se cruzam revelam um ponto de intersecção comum

Essa técnica revela o ponto ideal em exatamente três iterações. Uma quarta iteração mede o ponto ideal para confirmar e documentar o resultado.

A Figura 3 ilustra uma técnica para eliminar uma iteração usando informações de fronteira empiricamente conhecidas no plano x-y. Selecione o ponto inicial em um dos pontos de limite para que a primeira curva (A) seja um arco de 90 graus. Selecione o segundo ponto no primeiro arco movendo-se na direção x ou y.

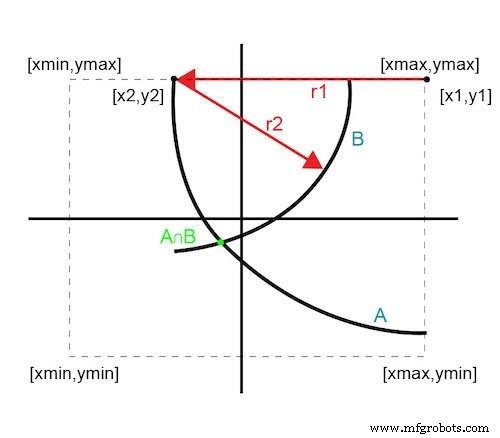
Figura 3. Solução de duas iterações

Como o segundo ponto ainda está na borda do limite, sua curva é um arco de menos de 180 graus. A interseção dessas duas curvas fornece um único ponto ótimo. Essa abordagem revela o ponto ideal em apenas duas iterações e o confirma com três.

Aproximação sucessiva do círculo

A solução ótima depende da precisão da equação matemática. Em uma situação real de medição, várias suposições ou erros afetarão os resultados. Os sinais medidos são muito pequenos; o ruído e as tolerâncias de medição introduzem erros. Usar círculos perfeitos em vez de elipses introduz algumas incertezas. As suposições do fator de escala necessárias para resolver várias equações também introduzem incerteza. Esses erros e suposições se traduzem em imprecisão nas curvas.

A Figura 4 ilustra como as curvas difusas não garantem um ponto de interseção exato; em vez disso, eles definem uma área de convergência.

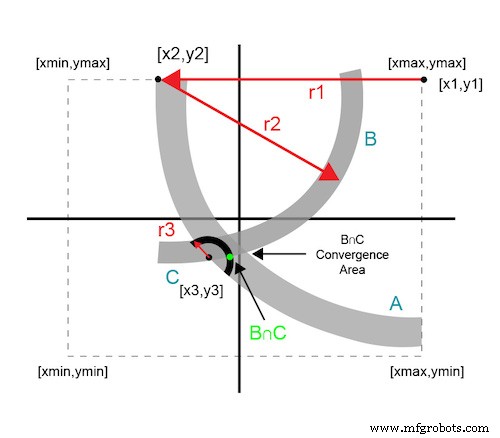
Figura 4. Aproximação de intersecção sucessiva do círculo

Cada ponto de dados adicional usa os dados da iteração anterior. Círculos sucessivos convergem para uma área de solução que está dentro do limite mínimo do sistema.

Exemplo de medição

O exemplo usa o AFE7070 DAC e otimiza para o parâmetro de passagem da portadora. O AFE7070 é uma plataforma conveniente, já que o DAC e o modulador estão integrados. O desequilíbrio de deslocamento DC nas entradas de quadratura do modulador determina o desempenho do feedthrough da portadora. O AFE7070 possui um recurso de sintonia digital interna para controlar minuciosamente o balanço DC offset. Não é preciso muito; a resolução está na escala de microvolts.

Os parâmetros x, y para o exemplo são valores inteiros de etapas digitais que controlam o nível DC nas entradas em quadratura. A amostragem estatística anterior do dispositivo forneceu os limites x, y das variáveis ​​de entrada, bem como as tabelas de etapas usadas nos cálculos. As tabelas de etapas fornecem uma "conversão" de um feedthrough de transportador medido em decibéis miliwatts para um fator delta-x (ou delta-y).

Um valor medido alto (ou em outras palavras, ruim) significa que a configuração está errada e precisa de um delta maior para atingir o ponto ideal. Por outro lado, um valor baixo significa que o ponto de ajuste está próximo e precisa de uma pequena correção. Este pequeno “trabalho de casa” é necessário para garantir que os pontos iniciais não estejam muito distantes e para reduzir o tempo de iteração ao mínimo.

A Figura 5 mostra o algoritmo Python que encontra as variáveis ​​de entrada ideais em quatro iterações ou menos.

Figura 5. Algoritmo de otimização Python

As funções “Get_r” e “GetCFi” são medidas específicas do dispositivo. Omiti o código por questões de brevidade, pois ele é irrelevante para a demonstração do algoritmo de otimização. Em suas aplicações, essas funções são pertinentes à programação e medição do parâmetro do dispositivo em seu sistema.

Conclusão

Para o AFE7070 DAC, na maioria dos casos, o algoritmo otimiza o feedthrough do portador em três iterações e em menos de 1,7 s, bloqueado principalmente pelo tempo de configuração e varredura do analisador de espectro. Os métodos da etapa anterior levaram quase 20 iterações e mais de 20 s para serem concluídos. Este algoritmo representa uma melhoria de velocidade de mais de 10 vezes em comparação com a abordagem tradicional. Outros parâmetros do sistema de comunicação dependentes de variáveis ​​de entrada ortogonais de ganho e fase também podem usar este algoritmo para localizar com eficiência uma solução ótima.

Artigos do setor são uma forma de conteúdo que permite aos parceiros do setor compartilhar notícias, mensagens e tecnologia úteis com os leitores do All About Circuits de uma forma que o conteúdo editorial não é adequado. Todos os artigos da indústria estão sujeitos a diretrizes editoriais rígidas com a intenção de oferecer aos leitores notícias úteis, conhecimentos técnicos ou histórias. Os pontos de vista e opiniões expressos nos Artigos da Indústria são do parceiro e não necessariamente da All About Circuits ou de seus redatores.