Predição do efeito Hall anômalo quântico em MBi e MSb (M:Ti, Zr e Hf) Favos de mel

Resumo

As inúmeras possibilidades de descoberta de novos materiais têm impulsionado o esforço de pesquisa no campo da física dos materiais. Apenas recentemente, o efeito hall anômalo quântico (QAHE) foi realizado em isoladores topológicos magnéticos (TIs), embora existindo em temperaturas extremamente baixas. Aqui, predizemos que os favos de mel MPn (M =Ti, Zr e Hf; Pn =Sb e Bi) são capazes de possuir fases de isolamento QAH com base em cálculos de estrutura eletrônica de primeiros princípios. Descobrimos que os sistemas de favo de mel HfBi, HfSb, TiBi e TiSb possuem QAHE com a maior lacuna de banda de 15 meV sob o efeito da deformação de tração. No favo de mel HfBi de baixa fivela, demonstramos a mudança do número de Chern com o aumento da constante de rede. Os cruzamentos das bandas ocorreram em pontos de baixa simetria. Também descobrimos que, variando a distância de flambagem, podemos induzir uma transição de fase de modo que o cruzamento da banda entre dois orbitais Hf d ocorra ao longo do ponto de alta simetria K2. Além disso, os estados de borda são demonstrados em nanofitas de zigue-zague HfBi empenadas. Este estudo contribui com novos materiais adicionais para o conjunto atual de isoladores QAH previstos que têm aplicações promissoras em spintrônica.

Histórico

Rigorosos esforços de pesquisa têm sido continuamente focados na exploração de novos materiais 2D, como isoladores quantum spin Hall (QSH). Esses novos materiais, também conhecidos como isoladores topológicos bidimensionais (TIs 2D), apresentam uma propriedade única em que as bordas possuem estados sem intervalos polarizados de spin, apesar do sistema em massa ser um isolador [1]. Os isoladores QSH apresentam transporte de spin / carga sem dissipação, o que é altamente importante em aplicações de dispositivos spintrônicos [2]. Recentemente, foi descoberto que a quebra da simetria de reversão do tempo (TRS) em isoladores QSH leva a um sistema de efeito Hall anômalo quântico (QAHE) no qual estados de borda helicoidal são convertidos em estados de borda quirais [3]. O transporte de carga sem dissipação sem a necessidade de um campo magnético externo fornece aplicações promissoras em spintrônica de baixo consumo de energia [4, 5] e tem incentivado a busca por mais sistemas QAHE [6, 7]. Previsto por Haldane em 1988, o QAHE só foi obtido experimentalmente em 2013 por dopagem magnética de filmes finos de isoladores topológicos [8]. Estudos teóricos sugeriram que a fase Hall anômala quântica (QAH) pode ser alcançada quebrando o TRS de um TI introduzindo ferromagnetismo e induzindo uma transição de inversão de banda por fortes efeitos de acoplamento spin-órbita (SOC) [9, 10]. Assim, os isoladores QSH são bons materiais de partida para alcançar o QAHE. Vários estudos previram que filmes finos dos grupos IV (Sn) [11–13] e V (Bi, Sb) [6, 14–17] suportam fases QSH que também podem ser alcançadas via funcionalização química [17, 18]. Além dos elementos do grupo IV e V, também foi previsto que os favos de mel [19–21] III-V suportam a fase QSH em casos independentes e funcionalizados. Esses resultados abriram caminho para encontrar as fases do QAHE. Estudos mostraram que QAHE foram encontrados em filmes finos funcionalizados do grupo IV [22] e V [17, 18, 22]. Além disso, os cálculos dos primeiros princípios mostram QAHE em favos de mel fluorados [23] e quimicamente funcionalizados [24] III-V. Além disso, vários estudos teóricos previram que a dopagem de metais de transição em favos de mel pode induzir fases de QAH [17, 25-27]. Isso foi realizado experimentalmente por meio de dopagem com Cr e V [8, 28, 29]. Apoiado pela descoberta de que os materiais do favo de mel III-V são isoladores QSH [19] e a previsão teórica de que a dopagem de um material magnético pode induzir magnetismo [10], substituímos o elemento do grupo III por um metal de transição (M =Ti, Zr e Hf). Carbonetos de metais de transição MC (M =Zr e Hf) [30] e haletos de metais de transição MX (M =Zr e Hf) [31] também são outra família de materiais previstos para existirem como isoladores QSH. No entanto, seu potencial para apoiar QAHE ainda não foi explorado. Motivados por essas descobertas, predizemos as propriedades eletrônicas dos pnictídeos de metais de transição MPn (M =Ti, Zr e Hf; Pn =Sb e Bi) para exibir a fase QAH. Neste trabalho, empregamos cálculos de primeiros princípios para prever a capacidade dos metais de transição (M =Ti, Zr e Hf) de induzir magnetismo intrínseco em favos de mel Bi / Sb. Examinamos os casos flambados e planos e identificamos as mudanças de fase devido à deformação. As fases de QAH são verificadas calculando o número de Chern e observando a inversão de banda.

Resultados e discussões

Semelhante ao favo de mel Bi puro (com dois átomos na célula unitária), que pode adotar estruturas flambadas e planas, nosso material é obtido substituindo metade do Bi por um metal de transição [por exemplo, Ti, Zr e Hf] na célula unitária . A vista superior de M-Bi / Sb com uma célula unitária 1 × 1 delineada é mostrada na Fig. 1a, enquanto as vistas laterais dos favos de mel M-Bi / Sb curvados e planares são mostradas na Fig. 1b, c, respectivamente. A primeira zona de Brillouin (BZ) correspondente marcada com pontos de alta simetria é mostrada na Fig. 1d.

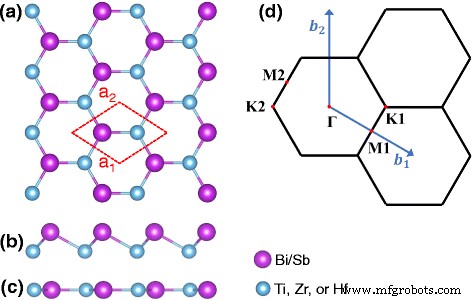
a Estrutura cristalina do favo de mel M-Sb / Bi. b , c Vistas laterais de estruturas flambadas e planas, respectivamente. d A primeira zona de Brillouin (BZ) com pontos de alta simetria

Nós estudamos a estabilidade dos favos de mel e o efeito da tensão, variando a constante de rede e permitindo que os átomos relaxem para os casos flambados e planos. Em seguida, identificamos suas fases topológicas sob diferentes deformações por meio dos cálculos do número de Chern. O resultado é ilustrado por meio de um diagrama de fase, conforme apresentado na Fig. 2. As curvas de energia para TiBi, ZrBi e HfBi são mostradas na Fig. 2a-c, respectivamente. Descobrimos que os favos de mel MBi possuem as fases de baixa curvatura e planar. Por meio dessas figuras, identificamos as constantes da rede de equilíbrio para análises posteriores. A figura também mostra que o MBi deformado é a estrutura energeticamente favorecida. No entanto, a maioria das fases de QAH são observadas quando a deformação é aumentada, o que transforma o material de favos de mel fivela em planos. Também deve ser observado que as fases de QAH podem ser observadas em HfBi encurvado, mas apenas dentro de uma pequena faixa de constantes de rede [ver Fig. 2c].

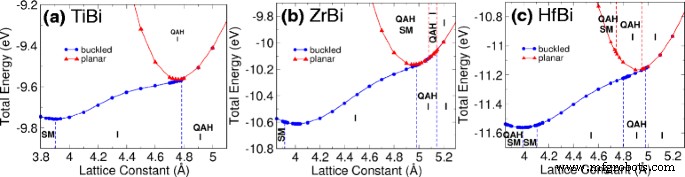
Diagrama de fase de a TiBi, b ZrBi e c HfBi mostrando a energia total em diferentes constantes de rede. O diagrama é dividido em várias regiões rotuladas como QAH (fase Hall anômala quântica), I (isolante) e SM (semimetal). Círculos azuis e triângulos vermelhos representam casos flambados e planos, respectivamente

As tabelas 1 e 2 mostram as constantes de rede de equilíbrio para as estruturas M-Bi e M-Sb. O gap associado, o momento magnético, a fase e a classificação do material também são indicados. QAHE está presente quando o número de Chern calculado, C, é um número inteiro diferente de zero. O gap é calculado como a diferença entre as bandas mais baixas desocupadas e as mais ocupadas. Nossos cálculos mostram que a fase isolante QAH pode ser encontrada em TiBi planar e HfBi com gap de 15 e 7 meV, respectivamente. Além disso, a transição de fase pode ser induzida em TiBi variando a distância deformada [ver Fig. 3] e induzindo deformação em HfBi deformado [Fig. 4]. No TiBi, descobrimos que os cruzamentos das bandas devido à variação da distância de flambagem ocorrem em pontos de baixa simetria mostrados na Fig. 3d; enquanto em HfBi, observamos os dois cruzamentos de banda (pontos de transição críticos) primeiro em K2 ( a =4,8 Å) e então em K1 ( a =5,0 Å) devido à deformação na Fig. 4c, g.

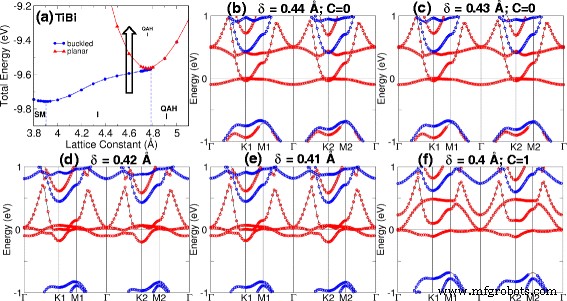
Transição de fase após variar a distância encurvada. a Diagrama de fase do TiBi em a =4,6 Å. A seta mostra o caminho da transição. b - f A transição da estrutura da banda como a distância de flambagem ( δ ) foi reduzido de 0,44 para 0,4 Å. A transição ocorre em δ =0,41 Å

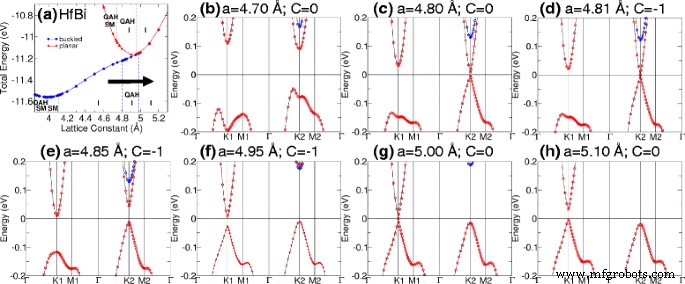
Transição de fase após variar a constante de rede. a Diagrama de fase do HfBi deformado. A seta mostra o caminho da transição. b - h A transição da estrutura de banda conforme a constante de rede foi aumentada de 4,7 para 5,1 Å

A Figura 5a, b mostra as estruturas de banda eletrônica nas constantes de rede de equilíbrio para M-Bi e M-Sb em estruturas planas e flambadas, respectivamente. Os círculos vermelhos e azuis são as contribuições para aumentar e diminuir a rotação, respectivamente. A fase QAH (com C =1) com a maior lacuna de banda é de 15 meV observada em TiBi planar. Planar HfBi também é um isolante QAH com um pequeno intervalo de banda de 7 meV (com C =-1). No entanto, em uma forma curvada, HfBi é um semimetal com um C alto =−3. Por outro lado, ZrBi, TiSb, ZrSb flambado e ZrSb planar são considerados isolantes triviais.

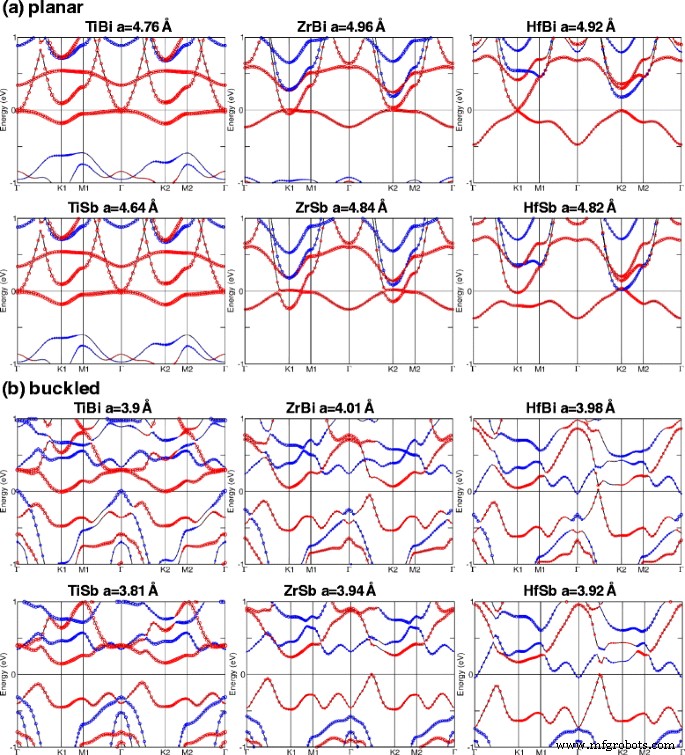
Estruturas de banda eletrônica de M-Pn (M =Ti, Zr e Hf; Pn =Sb e Bi) em suas constantes de rede de equilíbrio para a planar e b caixas de fivela. As constantes de rede de equilíbrio são fornecidas acima da estrutura da banda. Círculos vermelhos e azuis indicam + s _z e - s _z contribuições, respectivamente

A natureza do QAHE pode ser melhor compreendida examinando os efeitos do SOC em cálculos não magnéticos e ferromagnéticos. Para tanto, escolhemos TiBi planar (com a =4,76 Å) como exemplo. As estruturas de banda obtidas em cálculos não magnéticos e ferromagnéticos com e sem SOC são mostradas na Fig. 6. Nossos cálculos mostram que esta estrutura tem um momento magnético de 1,05 μ _B por célula unitária que é principalmente fornecida por átomos de Ti. Nos cálculos não magnéticos, descobrimos que o sistema é metálico [Fig. 6a, c]. Podemos observar na Fig. 6b que um momento magnético líquido pode ser induzido devido ao ordenamento ferromagnético que é influenciado pelo metal de transição, Ti. Além disso, o sistema agora tem estados de spin-up sem intervalos (linhas vermelhas) e estados de spin-down com intervalo, e aplicando SOC ao cálculo ferromagnético, um intervalo de 15 meV é então obtido. Isso mostra que a inversão de banda é induzida por SOC e a abertura do gap resulta em QAHE.

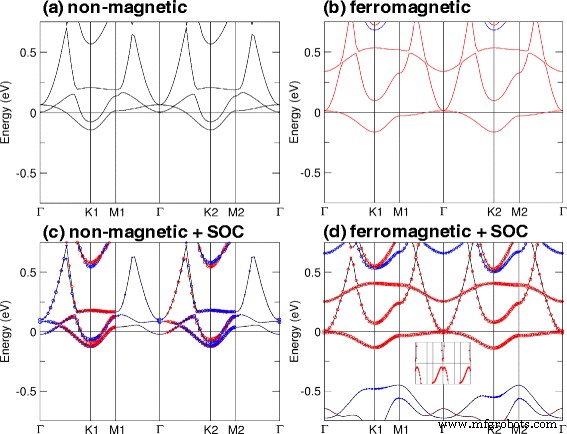
Estruturas de banda eletrônica do filme TiBi planar em a =4,76 Å para cálculos não magnéticos ( a ) sem SOC e ( c ) com SOC, bem como cálculos ferromagnéticos ( b ) sem SOC e ( d ) com SOC. Círculos vermelhos e azuis indicam + s _z e - s _z contribuições, respectivamente, para ( c ) não magnético ( d cálculos ferromagnéticos) com SOC

Finalmente, inspecionamos o espectro de banda de borda do favo de mel HfBi planar para a presença de estados de borda usando Hamiltonianos de ligação forte derivados por meio de funções de Wannier. Construímos fitas HfBi com bordas em zigue-zague e largura de 127 Å como mostrado na Fig. 7. A figura também confirma a presença de estados de borda denotados por e proporcionais ao tamanho dos círculos vermelhos e azuis que representam as bordas direita e esquerda, respectivamente . Os estados de borda separados são devidos à assimetria das bordas em zigue-zague direita e esquerda. Também podemos observar um número ímpar de bandas de borda cruzando o nível de fermi. Descobrimos que este número é igual ao valor absoluto do número Chern, confirmando ainda mais a fase QAH no HfBi planar.

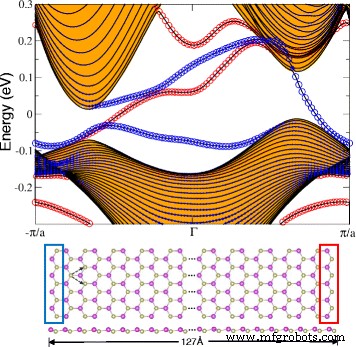
Estrutura da banda ao longo da borda do nanoribão em zigue-zague HfBi curvado com a =4,9 Å e a largura de 127 Å. Círculos azuis (vermelhos) indicam a contribuição das bordas esquerda (direita). As bandas em massa são denotadas pela região preenchida com laranja

Além disso, calculamos o espectro de fônons para cada sistema e observamos que esses sistemas possuíam frequência negativa. Assim, os sistemas acima mencionados precisariam de um substrato para estabilizar. Notamos também que os cálculos mencionados acima foram feitos usando uma célula unitária um a um, e os materiais com configuração ferromagnética (FM) é o estado mais estável. No entanto, para uma supercélula maior, descobrimos que FM ainda tem uma energia mais baixa do que a configuração anti-ferromagnética (AFM) nos casos flambados, enquanto as configurações FM e AFM são degeneradas em energia nos casos planos.

Conclusões

Para resumir, nossos cálculos de primeiros princípios prevêem que a substituição de metais de transição (Ti, Zr e Hf) em filmes de favo de mel Sb ou Bi pode potencialmente exibir a fase QAH. Embora esses materiais sejam energeticamente mais estáveis em sua forma curvada, transformá-los para a forma plana produz a fase QAH em uma faixa bastante razoável de constantes de rede. Essa fase também pode ser induzida variando a distância de flambagem e aplicando tensão como deveria em nossos diagramas de fase calculados. Descobrimos que as estruturas planares de TiBi e HfBi existem como isolantes QAH com um gap de 15 e 7 meV, respectivamente. Essas descobertas oferecem outra maneira de realizar a fase QAH em materiais em favo de mel que podem ser potencialmente úteis em aplicações spintrônicas.

Métodos / Experimental

Os cálculos dos primeiros princípios dentro da estrutura da teoria funcional da densidade (DFT) foram realizados usando a aproximação de gradiente generalizado (GGA) [32-36] e o método de onda aumentada do projetor (PAW) [37] conforme implementado na Simulação de Viena Ab-Initio Pacote Versão 5.3 (VASP) [38, 39]. O corte de energia cinética foi definido para 350 eV e as estruturas cristalinas foram otimizadas até que as forças residuais não fossem maiores que 5 × 10 ⁻³ eV / Å. O critério de autoconsistência para convergência foi definido em 10 ⁻⁶ eV para cálculos de estrutura eletrônica com ou sem acoplamento spin-órbita. Simulamos um filme fino inserindo uma camada de vácuo de pelo menos 20 Å ao longo do z em uma zona de Brillouin 2D amostrada de grades de Monkhorst-Pack centradas em gama 24 × 24 × 1 [40]. Calculamos as funções Wannier maximamente localizadas usando o pacote WANNIER90 [41] que foram então usados para calcular os estados de borda. As fases topológicas foram identificadas pelo cálculo do número de Chern usando o pacote Z2Pack [42, 43] que utiliza uma técnica que rastreará centros de carga Wannier híbridos.

Dependência da toxicidade das nanopartículas em suas propriedades físicas e químicas Preparação de moagem de esferas em uma etapa de nanoescala CL-20 / óxido de grafeno para sensibilidade e tamanho de partícula significativamente reduzidos

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias