Dieletroforese de ondas moduladas por frequência de vesículas e células:inversões periódicas na frequência de cruzamento

Resumo

Formulamos a força dieletroforética exercida sobre micro / nanopartículas na aplicação de campos elétricos modulados em frequência (FM). Ajustando a faixa de frequência de uma onda FM para cobrir a frequência de crossover f _X na parte real do fator de Clausius-Mossotti, nossa teoria prevê a reversão da força dieletroforética cada vez que a frequência instantânea atravessa periodicamente f _X . Na verdade, observamos inversões periódicas em U de vesículas, células de leucemia e hemácias que sofrem dieletroforese por ondas FM (FM-DEP). Também é sugerido por nossa teoria que o rastreamento de vídeo das curvas em U devido ao FM-DEP está disponível para a medição ágil e precisa de f _X . O método FM-DEP requer uma curta duração, menos de 30 s, ao aplicar a onda FM para observar várias voltas em U e a agilidade na medição f _X é muito útil não apenas para suspensões de células salgadas, mas também para nanopartículas, porque o fluxo de solvente induzido por campo elétrico é suprimido o máximo possível. A precisão de f _X foi verificado usando dois tipos de experimento. Primeiro, medimos a força atrativa exercida em uma única vesícula experimentando dieletroforese de corrente alternada (AC-DEP) em várias frequências de campos elétricos sinusoidais. A dependência da frequência da força dieletroforética produz f _X como uma frequência característica na qual a força desaparece. Comparando o resultado AC-DEP de f _X com o obtido pelo método FM-DEP, ambos os resultados de f _X foram encontrados para coincidir uns com os outros. Em segundo lugar, investigamos as dependências de condutividade de f _X para três tipos de célula, alterando os eletrólitos circundantes. A partir dos resultados experimentais, avaliamos simultaneamente as condutividades citoplasmáticas e as capacitâncias da membrana usando uma teoria elaborada sobre o modelo de camada única de células biológicas. Enquanto as condutividades citoplasmáticas, semelhantes para essas células, foram ligeiramente menores do que a faixa de relatos anteriores, as capacitâncias de membrana obtidas estavam em boa concordância com aquelas relatadas anteriormente na literatura.

Histórico

A polarizabilidade de um fenótipo elétrico se deve principalmente à membrana celular e às propriedades elétricas citoplasmáticas que dependem da frequência do campo elétrico aplicado. Por conseguinte, as células individuais podem ser identificadas pelas diferenças nos espectros dielétricos usando técnicas elétricas não invasivas. As técnicas elétricas são atualmente competentes para separar células com fenótipos úteis de amostras desconhecidas [1-15]. Em comparação com outros métodos de separação, eles oferecem a principal vantagem de que a modificação celular por anticorpos ou aderência a material estranho é desnecessária, pelo que o potencial de dano celular ou ativação por essas sondas é evitado [1-16]. A caracterização das propriedades dielétricas celulares foi realizada principalmente usando espectroscopia de impedância [10, 12, 13] ou eletrocinética de corrente alternada (AC), como dieletroforese (DEP), DEP de onda viajante (twDEP) e eletrorrotação [1, 9, 15]. Entre eles, nos concentramos em estender o método AC-DEP para desenvolver um novo método para caracterização dielétrica usando ondas moduladas em frequência (FM) em vez de campos AC.

Em geral, a DEP ocorre em um gradiente de campo elétrico que cria uma força eletrocinética exercida sobre qualquer objeto polarizável, carregado ou neutro, na direção determinada não apenas pelo vetor gradiente, mas também pela parte real do Clausius-Mossotti ( CM) fator [1-15, 17-21]. Por exemplo, consideramos a força DEP induzida pelo campo elétrico CA E _AC ( r , t ) cuja dependência espaço-temporal é expressa como E _AC ( r , t ) = A ( r ) cos θ _AC ( r , t ) usando o vetor de amplitude A ( r ) e a fase θ _AC ( r , t ) A força AC-DEP é gerada pelo gradiente espacial da amplitude (ou seja, ∇ A ) multiplicado pela parte real do fator CM, conforme mencionado acima, enquanto o gradiente espacial da fase (ou seja, ∇ θ _AC ) multiplicado pela parte imaginária do fator CM cria a força do twDEP ou da eletrorrotação, que, portanto, fornece informações complementares ao método AC-DEP em termos de caracterização dielétrica [9, 15, 20, 21].

Nesta carta, pretendemos formular a força DEP induzida por um campo FM e comparar os métodos AC- e FM-DEP, de forma que nem o campo AC nem o FM considerem a dependência espacial da fase; portanto, definiremos θ _AC ( t ) =2 π f _AC t em proporção à frequência aplicada f _AC . Uma característica significativa do AC-DEP é que a direção da força, bem como sua força dependem de f _AC . Mais notavelmente, a direção da força é invertida na frequência de cruzamento f _AC = f _X devido à mudança no sinal da parte real do fator CM, que foi encontrada disponível para a caracterização dielétrica usando AC-DEP [1–15].

A dependência da frequência da força AC-DEP também possibilitou as seguintes manipulações [1-15, 22-31]:captura eletricamente controlável, focalização e translação de partículas coloidais, bem como o fracionamento e caracterização de seres vivos e / ou células mortas. Os sistemas convencionais para a montagem dieletroforética e / ou manipulação de partículas coloidais muitas vezes fazem uso de eletrodos microfabricados entre os quais o campo elétrico CA foi aplicado a suspensões coloidais, beneficiando-se dos avanços rápidos recentes na fabricação de dispositivos semicondutores integrados [24-30] . Essa tecnologia, que oferece manipulação sem contato, está atualmente sendo integrada a uma variedade de sistemas lab-on-a-chip que oferecem a vantagem de um manuseio preciso e repetível. No entanto, os eletrodos on-chip que criam pontos de alta intensidade em campos AC são incapazes de mudar suas posições independentemente do porta-amostra, ao contrário do foco do laser que pode ser posicionado livremente na manipulação óptica. Conclui-se da limitação dos sistemas on-chip que os métodos DEP anteriores apresentavam alguma dificuldade e complexidade na execução dos tipos de operações para as quais as pinças ópticas são adequadas. Um método candidato para superar essas dificuldades é o DEP dirigido por imagem óptica [32].

Aqui, adotamos, como uma alternativa mais simples, uma das técnicas de pinças eletrônicas [22, 23, 33-38] para montagem dieletroforética sob demanda e / ou manipulação sem um aparelho óptico (ver Fig. 1). Como visto na Fig. 1, nosso sistema estilo plug-in usa um par de agulhas de microeletrodo que são controladas por micromanipuladores para aplicar os campos elétricos externos em uma suspensão coloidal. As sondas de eletrodo não eram fixas, mas sim móveis em suspensões coloidais devido ao seu estilo de plug-in. Resta, no entanto, um requisito significativo para o uso prático da caracterização dielétrica:a duração pela qual um campo elétrico é aplicado às células circundadas por eletrólitos salgados deve ser minimizada. Por exemplo, o método AC-DEP envolve o uso de eletrodos interdigitados em forma de pente que são incorporados em um sistema microfluídico para que os campos AC de várias frequências possam ser aplicados simultaneamente em uma suspensão de células [24-30]. Embora tais sistemas refinados no chip tenham sido considerados relevantes para a caracterização dielétrica, a técnica do par multieletrodo é inaplicável ao sistema de par de eletrodo único que tem sido frequentemente usado nas técnicas de pinças eletrônicas [22, 23, 33-38] .

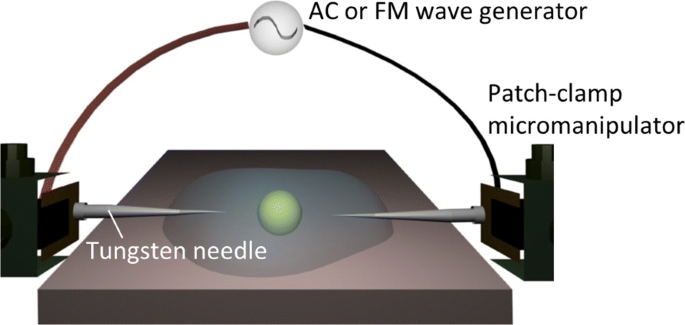
Configuração experimental. Um esquema do sistema de manipulação dieletroforética ilustrando o campo elétrico AC ou FM aplicado a uma partícula alvo através de um par de agulhas de eletrodo controladas por micromanipuladores patch-clamp

Para realizar medições simultâneas de multifreqüência usando o sistema de par de eletrodo único (Fig. 1), a mudança no campo elétrico aplicado deve ser investigada. Nesta carta, abordamos a disponibilidade de DEP variável no tempo devido a uma onda FM (FM-DEP) da seguinte forma:
$$ \ boldsymbol {E} (\ boldsymbol {r}, t) =\ boldsymbol {A} (\ boldsymbol {r}) \ cos \ theta (t), $$ (1)
onde a fase θ ( t ) da onda FM está relacionada à frequência instantânea f ( t ) como 2 π f ( t ) = d θ ( t ) / d t e
$$ f (t) =f_ {c} + \ Delta f \ cos \ left (2 \ pi f_ {m} t \ right), $$ (2)
com f _m denotando a frequência de modulação. Usamos FM de banda larga satisfazendo Δ f / f _m ≫1, de modo que as condições de f _m / f ( t ), f _m / f _c , f _m / Δ f ≪1 será referido como o limite de banda larga (WBL) na formulação teórica fornecida abaixo.

Nesta carta, é dada atenção especial à relação entre a frequência característica de f _X e a trajetória do FM-DEP. Na próxima seção, descrevemos os materiais usados ​​e os detalhes do sistema de plug-in para induzir FM-DEP. A terceira seção fornece os resultados e a discussão que consiste em quatro partes. Em primeiro lugar, investigamos os detalhes da repetição de voltas em U de uma única célula de leucemia, quantificando a trajetória recíproca, cuja periodicidade é explicada pela frequência de modulação f _m , ou a oscilação periódica de f ( t ) dada pela Eq. (2) A seguir, explicamos a trajetória recíproca teoricamente derivando a força dieletroforética variável no tempo que modula de acordo com a frequência instantânea f ( t ) do campo FM satisfazendo a condição WBL. A forma obtida da força dieletroforética fornece a equação que determina o f _X das curvas em U observadas. Terceiro, medimos a magnitude da força dieletroforética em uma vesícula multilamelar (MLV) que foi anexada a uma agulha de eletrodo devido à atração do AC-DEP. A dependência da força com a frequência foi ajustada usando a equação espectral que foi determinada a partir da parte real do fator CM, de modo que f _X foi determinada como a frequência característica na qual a força atrativa devida ao AC-DEP desaparece. Porque o método FM-DEP também fornece f _X analisando a trajetória recíproca de uma MLV, avaliamos a extensão da coincidência entre as frequências de cruzamento avaliadas de AC- e FM-DEPs. Finalmente, ambas as condutividades citoplasmáticas e as capacitâncias da membrana de três tipos de células foram avaliadas a partir de f _X em função crescente da condutividade da solução, e os valores obtidos foram comparados com os relatados na literatura.

Métodos

Materiais

Para a preparação de vesículas multilamelares (MLVs), usamos 1,2-dioleoil-sn-glicero-3-fosfatidilcolina (DOPC) como lipídeos, adquiridos da Avanti Polar Lipids. As MLVs foram obtidas pelo seguinte procedimento. O DOPC (1 mL, 20 mM) dissolvido em clorofórmio / metanol (2:1 v / v ) foi seco com N ₂ gás, e o solvente foi completamente removido sob vácuo por mais de 12 h. O filme fino depositado no frasco de vidro devido à evaporação foi reidratado com água desionizada e incubado a 25 ° C por várias horas.

Duas linhas de células utilizadas nas experiências foram JKT-beta-del da linha de leucemia de células T humanas (TL) e CCRF-SB da linha de leucemia de células B humanas (BL). Ambos os tipos de células TL e BL foram usados ​​após 1 semana de incubação em uma incubadora umidificada que contém 5 % CO ₂ a 37, de modo que tínhamos as concentrações de células na faixa de 0,5 × 10 ⁶ para 1 × 10 ⁶ células / mL. O meio RPMI 1640 para a cultura de células foi suplementado com 10% de soro fetal de brovina e 100 mM de piruvato de sódio. As células foram sedimentadas por centrifugação a 370 g por 3 min duas vezes para que as células pudessem ser puramente ressuspensas em 1 ml do meio RPMI 1640 antes da pipetagem. As suspensões de células obtidas foram ainda diluídas usando a solução isotônica de sacarose 200 mM a fim de preparar o solvente com a condutividade necessária.

Também usamos células vermelhas do sangue humano (RB) dispersas nas seguintes suspensões. Amostras de sangue total recém-colhidas foram obtidas de voluntários saudáveis ​​com vinte e poucos anos. As células, suspensas em uma mistura de meio RPMI 1640 e hematócrito de 3,1%, foram diluídas usando a solução isotônica de sacarose 200 mM a fim de preparar o solvente com a condutividade necessária, bem como as células de leucemia acima. Todos os experimentos dieletroforéticos usando células RB humanas foram concluídos em 10 minutos após a coleta das amostras de sangue total.

Configuração experimental

As condutividades das suspensões celulares foram medidas usando um medidor de condutividade (SevenMulti, Mettler-Toledo, Columbus, OH, EUA). Um esquema do sistema de plug-in usado é mostrado na Fig. 1. Um campo elétrico externo com uma onda AC ou FM foi aplicado por meio de um gerador de forma de onda arbitrária (Agilent 33220A, Agilent Technologies, Santa Clara, CA, EUA) com uma corrente amplificador (F30PV, FLC Electronics, Partille, Suécia) ao qual microeletrodos do tipo plug-in foram conectados. Os microeletrodos compreendiam agulhas de tungstênio com um diâmetro de ponta de 0,5 μ m que foram controlados independentemente por dois conjuntos de micromanipuladores de patch-clamp (NMN-21, Narishige, Setagaya-ku, Tóquio, Japão). Em todos os experimentos a seguir, mantivemos a separação da ponta em 100 μ m ao aplicar os campos externos às suspensões acima, e a magnitude máxima foi definida como 0,5 kV / cm. O par de agulhas foi inserido em uma gota de amostra montada no microscópio óptico invertido (TE2000-U, Nikon, Minato-ku, Tóquio, Japão), e as micrografias ópticas foram obtidas usando uma câmera CCD (Retiga Exi, QImaging, Surrey, British Columbia, Canadá) com uma taxa de quadros de 25 fps; aliás, foi confirmado que a resolução de frequência das ondas FM devido à taxa de quadros estava sempre dentro das barras de erro de cada dado. A 50- μ A gota da suspensão foi montada na mesa de amostragem do microscópio óptico invertido, cuja temperatura foi mantida a 25 ° C por meio de controlador de calor.

A técnica de plug-in permite que o sistema simples execute várias manipulações sem contato de uma única célula, como empurrá-la para um canal estreito sem qualquer contato e orientá-la na direção desejada. Embora seja frequentemente necessário tratar as células em uma solução isotônica com sal, é mais fácil implementar as manipulações DEP acima de células rodeadas por água desionizada. No arquivo adicional 1:Filmes S1 a S3, o sistema plug-in induziu o AC-DEP de células de diatomáceas suspensas em água desionizada. Podemos ver no arquivo adicional 1:Filmes S1 a S3 que uma célula de diatomácea anisotrópica dispersa em água sem sal foi manipulada como uma etiqueta post-it por um par de microeletrodos entre os quais o campo elétrico AC (1 kV / cm) foi aplicado . As operações sem contato consistem em três etapas:(i) uma célula alvo foi primeiro girada em paralelo a uma parede de vidro carregada positivamente pela combinação de alinhamento dipolo a uma frequência de 30 kHz e mudança de posição de cada microeletrodo (Arquivo adicional 1:Filme S1 ), (ii) subsequentemente alteramos a frequência para 100 kHz para empurrá-la em direção à parede para fixar a célula de solicitação com cargas negativas na superfície do vidro eletrostaticamente (Arquivo adicional 1:Filme S2) e (iii) a frequência CA foi ajustada a 20 MHz para induzir o AC-DEP na direção oposta, de forma que a célula ligada eletrostaticamente pudesse ser retirada (Arquivo adicional 1:Filme S3).

Resultados e discussão

Observação experimental de uma célula de leucemia com FM-DEP

Nossos microeletrodos plug-in (ver Fig. 1) permitem que o campo elétrico seja aplicado às partículas que flutuam muito acima do substrato da amostra, o que é de uso prático para selecionar células apropriadas. Por exemplo, Arquivo adicional 1:Filme S4 ​​mostra que o par de microeletrodos foi controlado para se aproximar de uma célula de diatomácea triangular flutuante à qual aplicamos o campo elétrico CA com sua frequência saltando entre 100 e 500 kHz em intervalos de 0,5 s. No arquivo adicional 1:Filme S4, vemos a célula triangular saltando em um microeletrodo devido ao salto de frequência como um resultado preliminar antes da seguinte manipulação usando o FM-DEP.

Arquivo adicional 1:Filmes S5 e S6 mostram comportamentos típicos de várias células TL experimentando o FM-DEP, que são semelhantes aos de células de mamíferos manipuladas por uma pinça eletrônica usando um único eletrodo AC-DEP [36]. A Figura 2 mostra uma das trajetórias periódicas usando o gráfico 3-D de ( x , y ) ao longo do t eixo, onde uma coordenada relativa de ( x , y ) é atribuído à posição de célula temporária com a origem de (0, 0) localizada em um ponto específico em uma agulha de microeletrodo para extrair a configuração de célula-eletrodo. Enquanto o x eixo representa a tangente à superfície do eletrodo em (0, 0), o y eixo, perpendicular à tangente, reflete principalmente a projeção das voltas em U periódicas explicadas abaixo. Na Fig. 2, selecionamos uma célula TL flutuante à qual aplicamos o campo elétrico FM com sua frequência de modulação f _m definido como f _m =0,25 Hz na faixa de 200 kHz ≤ f ( t ) ≤ 3 MHz. Porque temos aquele Δ f / f _m , f ( t ) / f _m <10 ⁻⁵ , a condição WBL realmente se mantém, conforme mencionado após a Eq. (2)

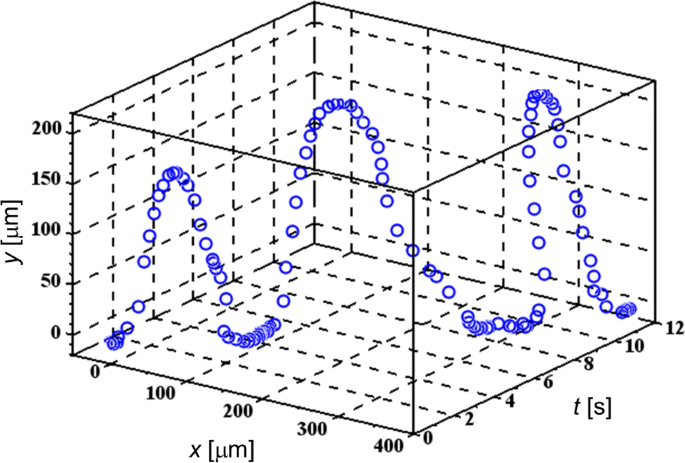
Trajetória 3D de uma célula TL alvo. Voltas em U periódicas devido à modulação de frequência são demonstradas para a célula TL submetida ao FM-DEP

Verifica-se no arquivo Adicional 1:Filmes S5 e S6, bem como na Fig. 2, que a trajetória periódica é constituída por três partes de saída, aproximação e permanência no microeletrodo:(i) a célula deixa o microeletrodo, (ii) ele se aproxima do microeletrodo após fazer uma volta em U e (iii) permanece na superfície do microeletrodo. A célula muitas vezes é incapaz de retornar à mesma posição na superfície do microeletrodo por causa do fluxo de solvente, que não é apenas observado no arquivo adicional 1:Filme S6, mas também é representado pelas voltas em U com a célula migrando no x direção na Fig. 2. Apesar da interferência com o fluxo do solvente, é possível distinguir os momentos em que a célula começa a deixar a superfície do microeletrodo e faz a volta em U na trajetória periódica, respectivamente. Assim, podemos ver na Fig. 2 que essas voltas em U são repetidas em intervalos de 4 s em coincidência com a frequência de modulação de 0,25 Hz, ou o período de 4 s da frequência instantânea f ( t )

Estudo teórico sobre FM-DEP

Para explicar as trajetórias experimentais, incluindo as voltas em U periódicas, consideramos um objeto esférico como um modelo simplificado de uma única célula, para a qual um campo elétrico variável no tempo arbitrário E ( r , t ) é aplicado. A Figura 3 mostra um esquema da força DEP dependente do tempo atuando em um objeto esférico [9]. Conforme mostrado na Fig. 3, a permissividade e condutividade dentro de um objeto esférico são representadas por ε _em e σ _em , respectivamente, e o subscrito “out”, como ε _fora e σ _fora , denota o exterior. Em geral, F _DEP ( r , t ) está relacionado ao momento dipolo induzido p ( r , t ) como [17-19]
$$ \ begin {array} {@ {} rcl @ {}} \ boldsymbol {F} _ {\ text {DEP}} (\ boldsymbol {r}, t) &=&\ left \ {\ boldsymbol {p} (\ boldsymbol {r}, t) \ cdot \ nabla \ right \} \ boldsymbol {E} (\ boldsymbol {r}, t), \ end {array} $$ (3)
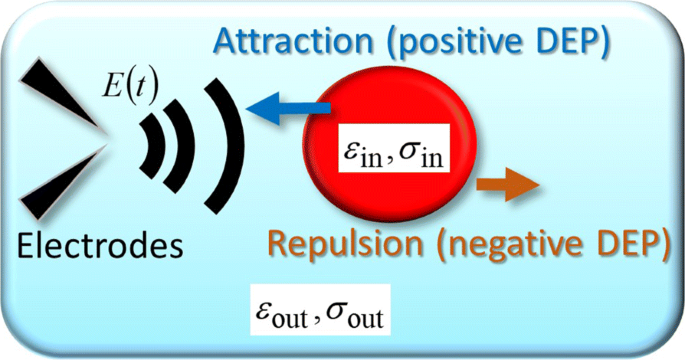
Modelo teórico. Representação esquemática da força FM-DEP exercida sobre uma célula que é modelada como um modelo de esfera homogênea tendo a permissividade e condutividade de ε _em e σ _em , respectivamente. A esfera é cercada por meio eletrolítico com sua permissividade e condutividade de ε _fora e σ _fora , respectivamente. O modelo de esfera homogênea é a simplificação do modelo esférico de camada única que considera a célula como um citoplasma manchado rodeado por uma membrana [9]
$$ \ begin {array} {@ {} rcl @ {}} \ boldsymbol {p} (\ boldsymbol {r}, t) &=&4 \ pi R ^ {3} \ epsilon _ {\ text {out}} K_ {H} \ left \ {\ boldsymbol {E} (\ boldsymbol {r}, t) + \ frac {\ tau} {\ Delta \ tau} \ widetilde {\ boldsymbol {E}} (\ boldsymbol {r}, t) \ right \}, \ end {array} $$ (4) $$ \ begin {array} {@ {} rcl @ {}} \ widetilde {\ boldsymbol {E}} (\ boldsymbol {r}, t ) &=&\ frac {1} {\ tau} \ int_ {0} ^ {tds} \, \ boldsymbol {E} (\ boldsymbol {r}, ts) e ^ {- s / \ tau}, \ end {array} $$ (5)
onde K _H e Δ τ são definidos da seguinte forma: K _H =( ε _em - ε _fora ) / ( ε _em +2 ε _fora ), e \ (\ Delta \ tau ^ {- 1} =\ tau _ {0} ^ {- 1} - \ tau ^ {- 1} \) usando o raio R do objeto esférico e dois tempos característicos de τ ₀ =( ε _em - ε _fora ) / ( σ _em - σ _fora ) e τ =( ε _em +2 ε _fora ) / ( σ _em +2 σ _fora )

Substituindo o campo elétrico CA E _AC ( r , t ) = A ( r ) cos (2 π f _AC t ) nas Eqs. (3) a (5), obtemos a força DEP média < F _DEP ( r , t )> que foi calculada a média ao longo dos ciclos do campo AC [9, 15, 20]:
$$ \ begin {array} {@ {} rcl @ {}} \ left <\ boldsymbol {F} _ {\ text {DEP}} \ right> &=&4 \ pi R ^ {3} \ epsilon _ {\ text {out}} K_ {H} \ left [\ left <\ boldsymbol {E} \ cdot \ nabla \ boldsymbol {E} \ right> + \ frac {\ tau} {\ Delta \ tau} \ left <\ widetilde { \ boldsymbol {E}} \ cdot \ nabla \ boldsymbol {E} \ right> \ right] \\ &=&\ chi (f _ {\ text {AC}}) \ nabla \ boldsymbol {A} ^ {2} _ {\ text {RMS}}, \ end {array} $$ (6)
onde A _RMS denota o vetor de raiz quadrada média (RMS) que satisfaz que \ (\ boldsymbol {A} _ {\ text {RMS}} ^ {2} =\ boldsymbol {A} ^ {2} / 2 \), e χ ( f _AC ) ≡2 π R ³ ε _fora Re [ K ( f _AC )] depende da frequência aplicada f _AC devido a Re [ K ( f _AC )], a parte real do fator CM [9, 15, 20]:
$$ \ begin {array} {@ {} rcl @ {}} \ chi (f _ {\ text {AC}}) =\ frac {2 \ pi R ^ {3} \ epsilon _ {\ text {out}}} {1+ (2 \ pi f _ {\ text {AC}} \ tau) ^ {2}} \ left \ {K_ {L} + (2 \ pi f _ {\ text {AC}} \ tau) ^ {2 } K_ {H} \ right \}, \ end {array} $$ (7)
onde K _L =( σ _em - σ _fora ) / ( σ _em +2 σ _fora ) e K _H , definidos acima, correspondem aos valores reais de CM nos limites de baixa e alta frequência, respectivamente, e esses valores de limite, K _L e K _H , precisa ter sinais opostos para que f _X definido por χ ( f _X ) =0 pode existir [9, 15, 20].

As equações (6) e (7) indicam que o campo elétrico CA cria a força DEP cuja direção depende da frequência aplicada f _AC por meio de χ ( f _AC ) dada pela Eq. (7), que explica a célula de diatomácea saltando no arquivo Adicional 1:Filme S4 ​​como segue (veja também a Fig. 3). Quando a frequência aplicada fornece o sinal de mais da parte real do fator CM (ou seja, χ ( f _AC )> 0), podemos observar células atraídas em direção às pontas das agulhas do eletrodo (o DEP positivo) nas quais a intensidade do campo AC, aplicada por meio de um par de agulhas de eletrodo, é maior. O sinal do fator CM real pode ser revertido para negativo em f _X , a frequência de desaparecimento do fator CM real (ou seja, χ ( f _X ) =0), onde temos a força dieletroforética zero conforme encontrada na Eq. (6). No sinal negativo do fator CM (ou seja, χ ( f _AC ) <0), os colóides individuais são repelidos do par de agulhas do eletrodo (o DEP negativo). A célula diatomácea triangular no arquivo Adicional 1:Filme S2 saltou devido à direção oposta dos AC-DEPs induzidos pelos campos AC com suas frequências de 100 e 500 kHz; combinando a Eq. (6) e as direções dieletroforéticas observadas, encontramos que χ (100 kHz)> 0 e χ (500 kHz) <0.

Em seguida, consideramos o FM-DEP plugando a fase dada pelas Eqs. (1) e (2) nas Eqs. (3) a (5). Conforme comprovado no arquivo adicional 2, a condição WBL da onda FM valida a forma aproximada da integração na Eq. (5), fornecendo assim
$$ \ left <\ widetilde {\ boldsymbol {E}} \ cdot \ nabla \ boldsymbol {E} \ right> =\ frac {1} {1 + \ {2 \ pi f (t) \ tau \} ^ { 2}} \ left (\ frac {\ nabla \ boldsymbol {A} ^ {2} _ {\ text {RMS}}} {2} \ right), $$ (8)
que se torna a mesma forma do AC-DEP quando a frequência dependente do tempo f ( t ) é substituído por uma frequência constante de f _AC . Obtemos assim a forma limite da força média DEP < F _DEP ( r , t )> que foi calculada em ciclos de θ ( t ) no campo FM (consulte as Eqs. (A1), (A13) e (A14) no arquivo adicional 2):
$$ \ begin {array} {@ {} rcl @ {}} \ left <\ boldsymbol {F} _ {\ text {DEP}} (\ boldsymbol {r}, t) \ right> =\ chi \ {f (t) \} \ nabla \ boldsymbol {A} ^ {2} _ {\ text {RMS}}, \ end {array} $$ (9)
sendo de uma forma semelhante à Eq. (6) para o AC-DEP. A diferença é se o coeficiente de χ { f ( t )} depende de t por meio de f ( t ), que muda ciclicamente de acordo com a modulação de frequência com o período de T _m =1 / f _m .

Com base na expressão simples (9) do FM-DEP, ilustramos com a Fig. 4 o mecanismo das curvas em U acima devido à onda FM. A Figura 4 mostra um esquema da DEP induzida pela onda FM na WBL quando a faixa de f ( t ) cobre a frequência de crossover f _X de modo que f _c - Δ f ≤ f _X ≤ f _c + Δ f . É suposto na Fig. 4 que a dependência da frequência da parte real do fator CM, ou χ { f ( t )}, fornece as mudanças de sinal alternativo da seguinte maneira:sinal de menos ( χ { f ( t )} <0) para f ( t ) < f _X e sinal de mais ( χ { f ( t )}> 0) para f ( t )> f _X , que é o caso de nossos experimentos. O primeiro período satisfaz f ( t ) < f _X tem um tempo de duração, enquanto o último f ( t )> f _X foi retido durante o resto do período:um ciclo é classificado em dois períodos marcados em vermelho e azul, respectivamente, na Fig. 4.

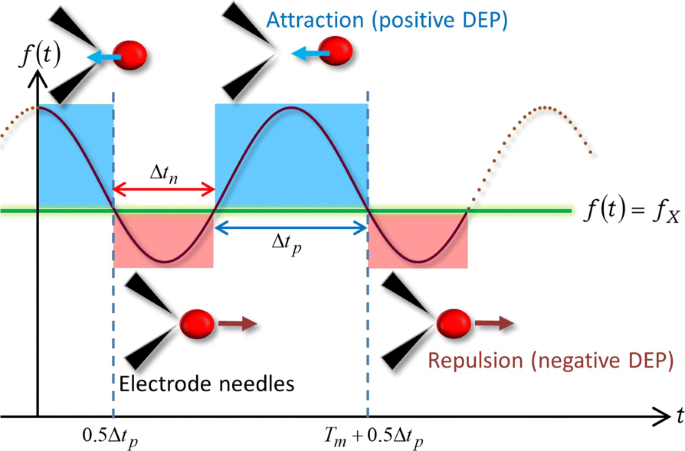
Força direção relacionada à modulação de frequência. Uma ilustração das voltas em U periódicas devido à onda FM com sua frequência dependente do tempo de f ( t ) cobrindo uma frequência de crossover f _X

Da mesma forma que o AC-DEP, Eq. (9) implica que o sinal de menos ( χ { f ( t )} <0) cria uma força repulsiva DEP entre a célula e os microeletrodos enquanto satisfaz que f ( t ) < f _X . Como resultado, a célula deixa a área ao redor das pontas das agulhas do microeletrodo entre as quais a magnitude do campo elétrico é maior:a célula experimenta o DEP negativo durante o período vermelho de Δ t _n na Fig. 4. No instante t _X como uma solução de f ( t _X ) = f _X , χ ( f ) desaparece, seguido pela mudança do sinal para χ ( f )> 0 enquanto f ( t )> f _X , e, correspondentemente, a força DEP é trocada para a força atrativa em t _X . Depois de fazer retorno em t _X devido à reversão na direção da força DEP, a célula alvo começa a se aproximar do microeletrodo migrando na direção oposta e é eventualmente presa entre as pontas das agulhas de eletrodo ou fixada em um dos eletrodos:a célula experimenta o DEP positivo durante o período azul de Δ t _p na Fig. 4. A Figura 4 indica que o ciclo de saída, aproximação e permanência no microeletrodo deve ser repetido com o período de modulação de T _m , de acordo com a Fig. 2: Δ t _n + Δ t _p = T _m . O mecanismo dieletroforético representado na Fig. 4 pode, portanto, explicar as voltas em U periódicas observadas no arquivo Adicional 1:Filmes S5 e S6, bem como na Fig. 2.

Vamos considerar a solução periódica da equação, f ( t _X ) = f _X . Como pode ser visto na Fig. 4, t _X é expresso como t _X = n T _m +0,5 Δ t _p = n T _m +0,5 ( T _m - Δ t _n ) usando um número inteiro de n =0, ± 1, ± 2, ⋯, que mais adiante lê
$$ 2 \ pi f_ {m} t_ {X} =(2n + 1) \ pi- \ pi f_ {m} \ Delta t_ {n}. $$ (10)
Substituindo a Eq. (10) na Eq. (2), temos para n =0 que
$$ f_ {X} =f_ {c} - \ Delta f \ cos \ left (\ pi f_ {m} \ Delta t_ {n} \ right), $$ (11)
esclarecendo que o método FM-DEP determina a frequência de crossover se o tempo de duração Δ t _n desde deixar o microeletrodo até fazer a volta em U pode ser medido com precisão.

Comparando frequências de cruzamento de um único MLV determinado a partir de FM- e AC-DEPs

Nós investigamos a precisão experimental da Eq. (11). Experimentalmente, muitas vezes é necessário que as células biológicas sejam dispersas em um eletrólito. Para MLVs, entretanto, o uso de água deionizada é permitido durante o processo de preparação de reidratação e diluição. Assim, usamos a suspensão de MLV sem sal para comparar as frequências de cruzamento determinadas de AC- e FM-DEPs.

As voltas em U dieletroforéticas de uma MLV alvo foram induzidas pela onda FM na faixa de 10 kHz ≤ f ( t ) ≤ 50 kHz (ou seja, f _c =30 kHz e Δ f =20 kHz) com uma configuração que f _m =0,1 Hz e, correspondentemente, o FM-DEP tem um período de 10 s. Nos experimentos, leva menos de 30 s para observar algumas voltas em U do MLV alvo, desde a saída até a aproximação dos microeletrodos. A partir da trajetória, obteve-se o tempo médio de saída que \ (\ overline {\ Delta t_ {n}} =5,8 \ pm 0,2 \) s. Porque a condição WBL se aplica ao presente experimento, satisfazendo que f _m / Δ f / f _m , f _, m / f ( t ) <10 ⁻⁵ , a frequência de cruzamento foi avaliada como f _X =35±1 kHz from substituting \(\overline {\Delta t_{n}}=5.8\pm 0.2\) s into Eq. (11).

For comparison, we made use of the programmable manipulator in the AC-DEP method that tries to evaluate the crossover frequency of the same targeted MLV to which the sinusoidal electric field with a frequency in the range of 30 to 100 kHz was applied via the electrode needle pair for inducing the AC-DEP. Because the programmable manipulator carries the electrode needle pair at a constant speed in one direction, we can measure the dielectrophoretic force similarly to the laser-trapping experiments [39]. Attaching the MLV on an electrode tip that undergoes uniform linear motion, not only the AC-DEP force but also the hydrodynamic force caused by the one-dimensional motion are exerted on the MLV. With the gradual increase of electrode velocity, F _DEP eventually becomes smaller than the hydrodynamic force. As a result, the MLV initially attached to the moving electrode, owing to the DEP attraction, is desorbed by the hydrodynamic force. Defining the critical value, v _c , by the maximum velocity value of the microelectrode pair prior to the desorption, the force balance equation between the DEP and hydrodynamic forces reads [39]
$$ F_{\text{DEP}}(f_{\text{AC}})=6\pi\eta R v_{c}, $$ (12)
onde F _DEP ( f _AC )e ≡<F _DEP> with the unit vector e defined by \(\boldsymbol {e}=\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}/|\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}|\), η the water viscosity at 25 °C and 2R the diameter of the MLV.

Additional file 1:Movies S7 and S8 demonstrates the force measurement using the above AC-DEP method at the applied frequency of f _AC =60 kHz. In Additional file 1:Movie S7, the velocity of the electrode pair controlled by the programmed manipulator is 110 μ m/s, which is lower than v _c ; therefore, the MLV remains attached to one part of the electrode pair owing to the dielectrophoretic attraction. Additional file 1:Movie S8, on the other hand, shows the higher electrode speed of 120 μ m/s, under which the dielectrophoretic force becomes smaller than the hydrodynamic force that is exerted on the MLV, thereby desorbing the MLV from the electrode. Accordingly, v _c is evaluated to be 110 μ m/s ≤v _c ≤ 120 μ m/s, and we can calculate F _DEP (60 kHz) using Eq. (12).

We can determine f _X from the experimental results of F _DEP at various external frequencies. Figure 5 shows the frequency dependence of F _DEP , indicating that the DEP force experienced by the MLVs was reduced by lowering the applied frequency. It is found from Eqs. (6) and (7) that the fitting function of F _DEP ( f _AC ) can be expressed as
$$ F_{\text{DEP}}(f_{\text{AC}})=\frac{L+(2\pi f_{\text{AC}}\tau)^{2}H}{1+(2\pi f_{\text{AC}}\tau)^{2}}, $$ (13)
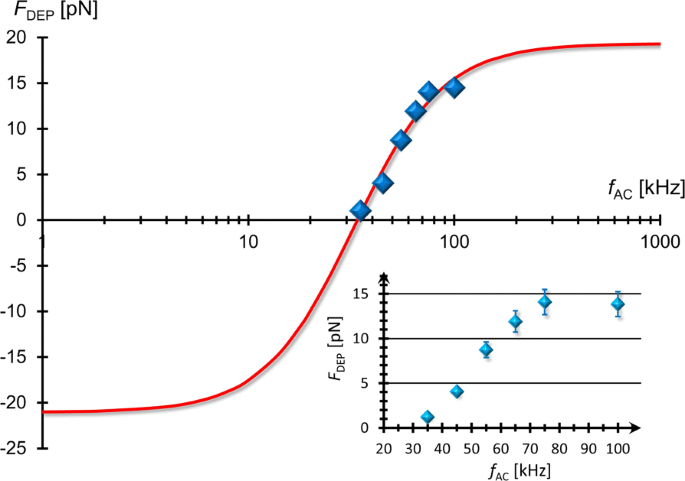
Frequency dependence of F _DEP . The FM-DEP force (F _DEP ) as a function of external frequency (f _AC ) of applied AC field where F _DEP has been evaluated from Eq. (12), the balance equation between the FM-DEP and hydrodynamic forces exerted on a single MLV. It can be seen that F _DEP is increased and saturated as f _AC is higher, reflecting a typical behavior of the relaxation spectrum of the real CM factor. The solid line represents the best-fit result of Eq. (13)

implying that
$$ f_{X}=\frac{1}{2\pi\tau}\sqrt{-\frac{L}{H}}. $$ (14)
Equation (13) is depicted by the solid line in Fig. 5 that has been fitted to the experimental data using the best-fit results of three parameters:L =−21.02 pN, H =19.03 pN, and τ =4.9 μ s. Substituting these results into Eq. (14), we evaluate that f _X =34.15 kHz, which coincides with the result of f _X =35±1 kHz evaluated from the FM-DEP method. The FM-DEP method is thus validated in terms of the consistency with the direct force measurement using the AC-DEP method.

Conductivity Dependencies of the Crossover Frequencies for Biological Cells

Let us return to the dielectrophoretic U-turns of biological cells mentioned in Fig. 2 to assess the practical reliability of the crossover frequencies when the FM-DEP method is applied to cell suspensions. Recently, an elaborate theory [40] has investigated, in more detail than before, the relationship between the homogeneous sphere model (see Fig. 3) and the single-shell model where the inner structure of cell is represented by a smeared-out cytoplasm surrounded by a membrane. As a result, the relation between f _X and the suspension conductivity σ _fora has been formulated using radius R of a cell, membrane capacitance C _m , and cytoplasmic conductivity σ _cyt [40]:
$$ f_{X}=\frac{1}{\sqrt{2}\pi {RC}_{m}}\left(\sigma_{\text{out}}-\frac{1}{2\sigma_{\text{cyt}}} \sigma_{\text{out}}^{2} \right)+f_{X0}, $$ (15)
onde f _{X 0} is the extrapolated value to the crossover frequency at σ =0 mS/m and will be treated as a fitting parameter herein. The elaborate treatment adds the squared term, the second term on the right hand side of Eq. (15), to the conventional linear relation which has mainly been used for evaluating C _m from f _X [40–45]. Theoretically, it has still been claimed [40] that Eq. (15) is valid within a lower range of σ _fora such that σ _fora <10 mS/m; however, it should be better to include the squared term in the evaluation of C _m , considering that our range of σ _fora is relatively high compared with previous results in the range of 10 mS/m ≤σ _fora ≤ 100 mS/m [40–45]. Hence, we determined σ _cyt as well as C _m from fitting Eq. (15) to the experimental results of f _X as an increasing function of σ _fora .

There are three kinds of biological cell used:TL and BL cells of human leukemia and RB cells of three human volunteers. In all the experiments using any species of cell, the conductivities were within the range of 60 to 160 mS/m, and the modulation frequency was set to be 0.25 Hz. Regarding the instantaneous frequency, most of the experiments adopted the range from 100 to 1.5 MHz (i.e., f _c =800 kHz and Δ f =700 kHz); exceptionally for leukemia cells, the frequency range was extended to 50 kHz ≤f ( t )≤1550 kHz (i.e., f _c =800 kHz and Δ f X =750 kHz) in the conductivity range of 60 mS/m≤σ ≤80 mS/cm because f _X in this σ -range has been found to be lower than 100 kHz, and we were unable to observe the DEP U-turns in the range of 100 kHz ≤f ( t )≤1500 kHz. Both of these frequency sets satisfy the WBL condition of Δ f /f _m , f ( t )/f _m <10 ⁻⁵ as before.

Each time we measured the leaving times of cells dispersed in a suspension, we looked for an appropriate spot at which a few cells having a similar size could simultaneously experience the FM-DEP above the substrate, and the microelectrode tips were placed at the measurable position using the micromanipulator. We continued such scanning inside the cell suspensions until the FM-DEP trajectories of 10 cells were collected in total at a couple of appropriate positions. For each kind of cell, the measurement of 10 cells was repeated twice using different drops of the same cell suspension. As mentioned, it is indispensable for the implementation of the FM-DEP measurement at each spot to suppress the electrically induced solvent flows as much as possible. Hence, we traced only two cycles of the U-turn path so that the duration time of applying the electric field could be adjusted to be less than 10 s, and, correspondingly, the leaving time of each cell is given as the average of each trajectory, including the two U-turns. The mean leaving time \(\overline {\Delta t_{n}}\) of each cell suspension is thus obtained from averaging the leaving times of 20 cells. Particularly for human RB cells, we further averaged three sets of the mean crossover frequencies obtained for three RB cell suspensions of three human beings, supposing that cells of the same species are similar in C _m and σ _cyt as well as in R . The two-step averaging of Δ t _n will be denoted by \(\left <\overline {\Delta t_{n}}\right>\). Substituting into Eq. (10) the experimental data of either \(\overline {\Delta t_{n}}\) or \(\left <\overline {\Delta t_{n}}\right>\), the mean crossover frequency <f _X > was obtained.

Figure 6 shows the σ _fora -dependencies of <f _X > measured for the above three kinds of biological cells using the FM-DEP method. The solid lines in Fig. 6 depict the best-fit results of Eq. (15). We evaluated C _m and σ _cyt from the best fitting of Eq. (15) into which the observed radii (R _obs ) were inserted. Table 1 lists the fitting results of C _m and σ _cyt , where we used the observed radii of 10 μ m ≤ 2R _obs ≤ 15 μ m for TL and BL cells, and 7.5 μ m ≤ 2R _obs ≤ 10 μ m for RB cells in evaluating C _m . It is to be noted from Table 1 that different species have different membrane capacitances, which are in good agreement with those reported in the literature [40–47]; the C _m values of RB cells with stationary whole blood samples from normal (healthy) donors are in excellent agreement with our value [46, 47], but are substantially higher than those of washed RB cells in isotonic buffered saline as noted in [47]. The best-fit results simultaneously provided cytoplasmic conductivities, which were consistently similar as seen from Table 1, but were slightly lower than the range of previous reports that 0.2 S/m ≤σ _cyt ≤1 S/m [40, 45, 48–51]. These results support that the FM-DEP method retains the practical reliability needed for the treatment of living cells.

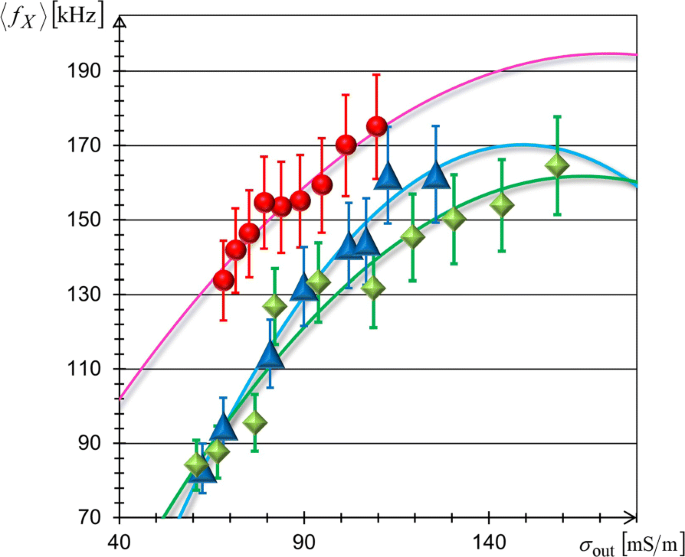
Conductivity dependences of crossover frequencies. Mean crossover frequency, <f _X >, of TL cells (blue triangles), BL cells (green diamonds), and RB cells (red circles) varying with increase of solution conductivity σ _fora . The best-fit results of Eq. (15) are delineated by the solid lines

Conclusões

Our theoretical treatment of the FM-DEP has mainly focused on the WBL condition. In this limit, we have proved theoretically that the direction of the FM-DEP force switches each time when the instantaneous frequency of the FM wave traverses the crossover frequency, thereby implying the periodic U-turns of micro/nanoparticles that undergo the FM-DEP. Two kinds of experiment have demonstrated the accuracy and reliability of f _X obtained from the observed trajectories of MLVs and cells using our formulation of the FM-DEP (Eqs. (9) and (11)):While the f _X evaluated from the FM-DEP of a single MLV coincides with that obtained from the force measurement of the same MLV experiencing AC-DEP, the conductivity dependencies of f _X provide the membrane capacitances of various cells that are in close agreement with the literature values. In other words, it has been validated theoretically and experimentally that the FM-DEP in the WBL limit can be mimicked by the time-varying AC-DEP induced by the AC wave with its frequency changing continuously according to the periodic function of f ( t ) The simple view applies to other electrokinetics, including the twDEP and the electrorotation by applying the FM wave that has the spatial dependence of the phase as well as the magnitude. The AC- and FM-DEPs are associated with the real part of the dielectric spectra (or the CM factor), whereas the electrokinetics due to the spatial gradient of the phase reflect the imaginary part of the CM factor as mentioned before. Therefore, the application of the FM wave to either twDEP or electrorotation will be required for completing the dielectric characterization (the dielectric spectroscopy, in general) using the electrokinetics.

We have treated microparticles such as MLVs and cells for the precise tracking of particle trajectories. In these experiments, sedimented particles as well as floating ones have been observed; we need to increase the magnitude of electric field for inducing the DEP of the sedimented particles which are likely to be aggregated. Accordingly, we have used the plug-in system for applying the FM wave to a targeted particle floating above the substrate.

It is promising to further develop the FM-DEP method for smaller particles with their sizes of submicron to nanoscale, such as dispersed carbon nanotubes, thereby opening up the possibility of real-time spectroscopy using the FM-DEP as described below. When we apply the FM wave to the smaller colloids using the on-chip systems whose electrode configuration is designed to create a constant gradient of the applied electric field, the time-varying velocity vector v ( t ) of the FM-DEP caused by the time dependence of the FM-DEP force is ascribed to the variation in χ ( f ) (or the real part of the CM factor):it is found from Eqs. (9) and (12) that
$$ \boldsymbol{v}(t)=\frac{\nabla\boldsymbol{A}^{2}_{\text{RMS}}}{6\pi\eta R}\chi\{f(t)\}. $$ (16)
Hence, measuring the velocity vector v ( t ) of a submicron to nanoparticle could provide the frequency dependence of the real part of the CM factor directly, which would be nothing but the electrokinetic FM spectroscopy.

Abreviações

AC:

Alternating current

BL:

B cell leukemia

CM:

Clausius-Mossotti

DEP:

Dielectrophoresis

DOPC:

1,2-Dioleoyl-sn-glycero-3-phosphatidylcholine

FM:

Frequency modulated

MLV:

Multilamellar vesicle

RB:

Red blood

RMS:

Root mean squared

TL:

T cell leukemia

twDEP:

Traveling wave dielectrophoresis

WBL:

Wide band limit

Fotodetector controlado por comprimento de onda baseado em nanobelt de CdSSe único Aprimoramento significativo de fotodetetores de metal semicondutor de metal MgZnO por meio de acoplamento com plasmons de superfície de nanopartículas de Pt