Channel Plasmon Nanowire Lasers com cavidades em V-Groove

Resumo

Um laser de nanofio de plasmon de canal híbrido baseado em nanofio semicondutor de núcleo-shell GaAs / AlGaAs e ranhura em V de prata é proposto. A estrutura do laser tem capacidade potencial de integração com guias de onda plasmônica, usando modos de canal de plasma-polariton em guias de onda plasmônica V-groove. As propriedades guia e lasing são calculadas numericamente usando o método dos elementos finitos. A partir dos resultados teóricos, o laser pode suportar o modo de orientação com um diâmetro mínimo de 40 nm. A emissão de laser pode acontecer em um limite relativamente baixo em torno de 2.000 cm ^{- 1} quando o diâmetro é maior que 140 nm. Um fator de Purcell bastante grande de 180 poderia ser alcançado para aumentar a taxa de emissão espontânea.

Histórico

Com geometria cilíndrica e forte confinamento bidimensional de elétrons, buracos e fótons, nanofio semicondutor independente é ideal para laser semicondutor com limite reduzido e tamanho compacto [1,2,3,4,5,6]. Até o momento, a emissão de lasing à temperatura ambiente foi realizada em nanofios de ZnO, GaN, CdS e GaAs, cobrindo o espectro óptico de ultravioleta a infravermelho próximo [7,8,9,10,11,12]. Para continuar diminuindo as dimensões dos nanofios além do limite de difração, lasers nanofios plasmônicos foram propostos e demonstrados experimentalmente, incluindo lasers nanofios plasmônicos híbridos e lasers nanofios plasmon de alta ordem [13,14,15]. Entre eles, os lasers híbridos de nanofios plasmônicos alcançaram um limite de dimensão muito menor. Recentemente, o laser nanofio plasmônico mostrou sua capacidade de integração com guias de onda plasmônica, usando os modos de canal plasmon-polariton (CPP) em guias de onda plasmônica em V-groove [16]. Os diâmetros adotados no experimento estão acima de 300 nm. Os CPPs são os polaritons do plasmon guiados por um sulco em forma de V esculpido em metal, que foi sugerido pela primeira vez teoricamente por Maradudin e colaboradores [17]. Os CPPs mostraram forte confinamento, baixo amortecimento e robustez contra a curvatura do canal em comprimentos de onda do infravermelho próximo [18,19,20].

Aqui, combinando a baixa dissipação de modos plasmônicos híbridos com o forte confinamento e integração com guias de ondas plasmônicos do modo CPP, propomos um canal híbrido de lasers de nanofio de plasmon (CPN) e investigamos numericamente as propriedades modais e de lasing. O laser CPN é composto por um nanofio de GaAs / AlGaAs de núcleo-casca e ranhura em V de prata que é separada por uma camada dielétrica ultrafina de MgF ₂ , em que o diâmetro do nanofio fica na faixa de 40 a 220 nm para explorar as propriedades de laser além do limite de difração. Devido à forma hexagonal do nanofio GaAs / AlGaAs, duas estruturas integradas de lasers CPN serão mostradas na próxima seção.

Estruturas de laser PPN

O esquema das estruturas do laser CPN é demonstrado na Fig. 1, onde o material de fundo é o ar, o material em cinza é prata, cuja permissividade é descrita pelo modelo Drude \ ({\ varepsilon} _r ={\ varepsilon} _ { \ infty} - {\ omega} _p ^ 2 / \ left ({\ omega} ^ 2 + j \ gamma \ omega \ right) \), com ε _∞ =3,7, ω _p =9,1 eV, e γ =0,018 eV [21]. O nanofio colocado na ranhura em V tem uma estrutura núcleo-concha, o material do núcleo é GaAs e o material da concha é AlGaAs. O núcleo de GaAs é passivado por uma fina camada de revestimento de AlGaAs de 10 nm para melhorar a eficiência radiativa [12]. Entre o nanofio e a ranhura em V está uma camada dielétrica ultrafina de MgF ₂ . Sua espessura é fixada em 5 nm para suportar a propagação de baixa perda sob forte confinamento óptico. Existem duas formas de integração de lasers CPN. O primeiro nós o chamamos de CPN-N (CPN-estreito-ângulo), como mostrado na Fig. 1a, c, onde o nanofio fica horizontalmente na superfície da ranhura em V com um ângulo estreito de 60 °. O nanofio tem dois lados em contato com a camada dielétrica e a superfície do entalhe em V, entre o lado inferior e o vértice do entalhe em V está o ar. O segundo nós o chamamos de CPN-W (CPN-grande angular) como mostrado na Fig. 1b, d, onde o nanofio se posiciona verticalmente na superfície da ranhura em V com um grande ângulo de 120 °. O nanofio não tem apenas o contato de dois lados, mas também um contato de vértice com a camada dielétrica e a superfície do entalhe em V.

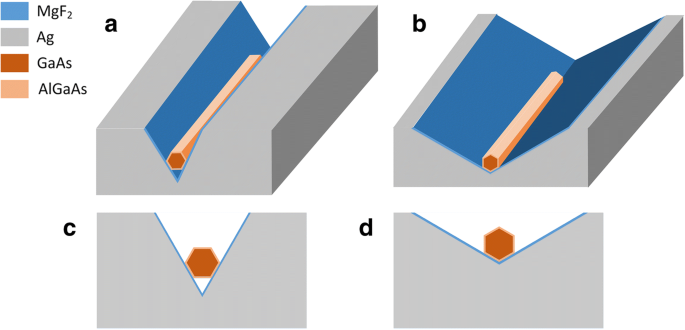
Diagrama esquemático das estruturas do laser CPN. a CPN-N. b CPN-W. c Seção transversal de CPN-N. d Seção transversal do CPN-W

Os modos de CPP suportados na ranhura em V dependem do ângulo e da profundidade da ranhura, especialmente o ângulo. Normalmente, o número de modos CPP suportados pela ranhura diminui com os ângulos crescentes, e em uma ranhura finitamente profunda, nenhum CPP pode existir na ranhura se o grau for maior que o grau crítico [22]. A localização forte do CPP pode ser alcançada em ranhuras com ângulos suficientemente pequenos [23], que também é mostrado na Fig. 2. Na Fig. 2a-c, a profundidade da ranhura é fixada em 1 μm, os ângulos da ranhura são de 10 ° , 30 ° e 60 °, respectivamente. O campo elétrico está fortemente localizado na parte inferior da ranhura com 10 °, formando o modo CPP. Já o campo elétrico começa a se distribuir em direção à borda da ranhura com 30 °, indicando que a localização se torna muito mais fraca. Com o ângulo de ranhura aumentado para 60 °, não existe CPP na ranhura. No entanto, como mostrado na Fig. 2d, e, com a integração do nanofio, o CPP ainda existe em grande angular de 60 ° e 120 ° (a profundidade é menor que 1 μm) e bem localizado dentro do MgF _{2 de baixo dielétrico} camada, que é totalmente diferente das ranhuras normais. Em uma estrutura plasmônica híbrida como a cavidade CPN, o acoplamento entre os modos dielétrico e plasmônico através da camada dielétrica ultrafina permite o armazenamento de energia "semelhante a um capacitor" que permite a propagação de luz em sub comprimento de onda em regiões não metálicas com campo eletromagnético nanolocalização [24]. Assim, o campo elétrico do CPP está fortemente localizado no MgF ₂ lacuna entre o nanofio e a ranhura, mesmo na ranhura com ângulos amplos. Propriedades adicionais de orientação e lasing em lasers CPN-N e CPN-W serão elaboradas na próxima seção.

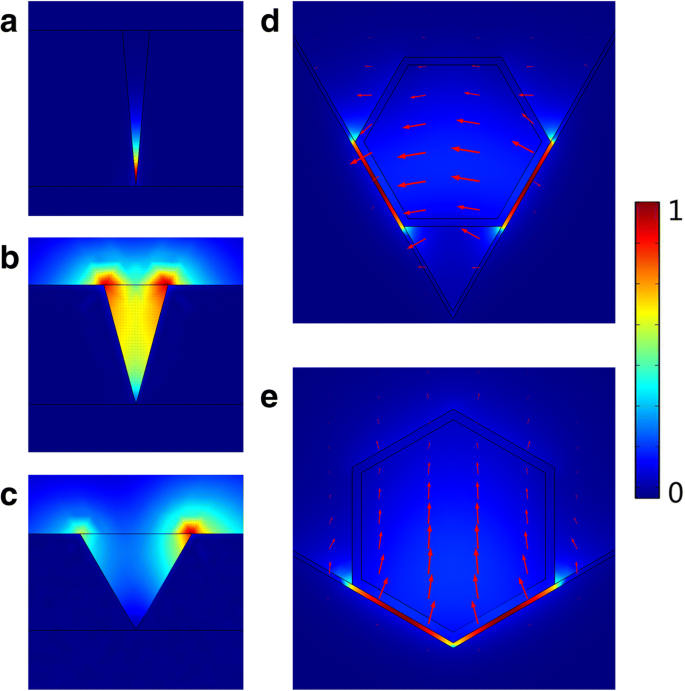
Distribuição de campo elétrico em a ranhura com 10 °. b Ranhura com 30 °. c Ranhura com 60 °. d Laser CPN-N. e Laser CPN-W. As setas vermelhas indicam a orientação do campo elétrico

Resultados e discussão

Com a vantagem dos modos plasmônicos híbridos, o campo elétrico pode ser localizado em dimensões além do limite de difração com propagação de baixa perda [25, 26]. Portanto, nossa investigação se concentra nas propriedades de guia e de laser na dimensão do diâmetro sub-onda, 40 a 220 nm. Embora seja um desafio controlar com precisão a posição do nanofio com diâmetro abaixo de 100 nm, uma condição mais ou menos ideal é considerada aqui para explorar o desempenho potencial dos lasers de CPN.

Como outros lasers de nanofios plasmônicos, mais modos guiados são suportados em lasers de CPN com diâmetros crescentes de nanofios. Conforme mostrado na Fig. 3, o nanofio com um diâmetro de 200 nm incorporado na ranhura pode suportar quatro modos guiados, HE _11x , HE _11y , TE ₀₁ e TM ₀₁ . A superfície da ranhura é paralela às laterais do nanofio, de modo que o ângulo da ranhura se mantém invariável conforme o diâmetro do nanofio muda. Em um laser nanofio plasmônico com substrato planar, o nanofio tem apenas um contato lateral com o substrato, levando ao acoplamento apenas entre os modos fotônicos de HE _11y e plasmons de superfície. Considerando que, em uma estrutura CPN, ambos HE _11x e HE _11y acoplar com plasmons de superfície formando modos plasmônicos de canal híbrido devido ao contato dos dois lados entre o nanofio e a superfície do sulco. Para os modos TE ₀₁ e TM ₀₁ , a energia eletromagnética dentro do nanofio também se acopla com os plasmons de superfície nos modos plasmônicos do canal de formação da superfície do sulco. Os quatro modos acima são os modos guiados em lasers CPN com diâmetro de 200 nm e os modos cortados com o diâmetro decrescente.

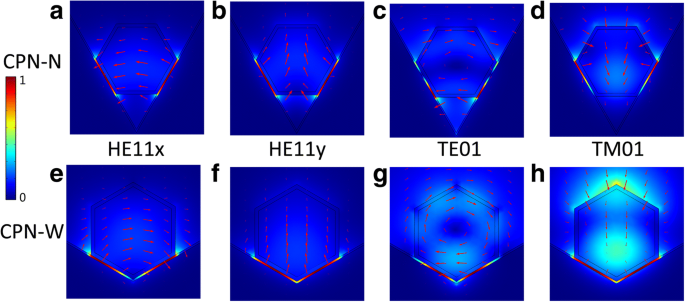
Distribuição de campo elétrico de modos em laser CPN-N ( a - d ) e laser CPN-W ( e - h ) O diâmetro do nanofio é fixado em 200 nm

Para investigar as propriedades de orientação e lasing do laser CPN, dependências da parte real do índice efetivo, perda modal, fator de confinamento modal e ganho de limiar no diâmetro do nanofio D são calculados e apresentados na Fig. 4a – d. Modos HE _11x , HE _11y , TE ₀₁ e TM ₀₁ de lasers CPN-N e CPN-W são investigados aqui. As propriedades dos lasers CPN-N e CPN-W são marcadas como símbolo de bloco com linha sólida e símbolo de círculo com linha tracejada, respectivamente. É importante notar que a profundidade do sulco aqui é muito maior do que o diâmetro do nanofio para eliminar a influência da borda do sulco. Conforme mostrado na Fig. 4a, há uma correlação positiva entre a parte real dos índices efetivos Re ( n _eff ) e diâmetro do nanofio D . Este se comporta da mesma forma que o índice efetivo de um nanofio individual. Com o aumento do diâmetro do nanofio, o índice equivalente da estrutura torna-se maior, levando ao aumento do índice modal. Conforme o diâmetro diminui, modo TE ₀₁ do laser CPN-W primeiro corta a 200 nm, depois o modo TM ₀₁ de corte de laser CPN-W em 180 nm e modos TE ₀₁ e TM ₀₁ do laser CPN-N ambos cortados em 170 nm, enquanto os modos fundamentais HE _11x e HE _11y têm diâmetros de corte menores. Devido à estrutura assimétrica dos lasers de CPN, o modo fundamental não degenera mais. Modo HE _11x tem o menor diâmetro de corte de 40 nm durante todos os modos em um laser CPN-N. Modo HE _11y tem o menor diâmetro de corte de 80 nm durante todos os modos em um laser CPN-W. Em um laser CPN-N, Re ( n _eff ) do modo HE _11x é maior do que o modo HE _11y . Considerando que, em um laser CPN-W, Re ( n _eff ) do modo HE _11y é maior do que o modo HE _11x , que resulta do componente perpendicular do modo fundamental. Normalmente, as direções do campo elétrico de HE _11x e TE ₀₁ são perpendiculares a HE _11y e TM ₀₁ , respectivamente. Nos lasers CPN-N e CPN-W, os ângulos do sulco são 60 ° e 120 °, resultando que x -componente de modos dominam em lasers CPN-N e y -componente de modos dominam em lasers CPN-W, como mostrado na Fig. 2d, e. Assim, modos HE _11x e TE ₀₁ tem Re maior ( n _eff ) e diâmetros de corte menores em um laser CPN-N, enquanto os modos HE _11y e TM ₀₁ tem Re maior ( n _eff ) e menor diâmetro de corte em um laser CPN-W.

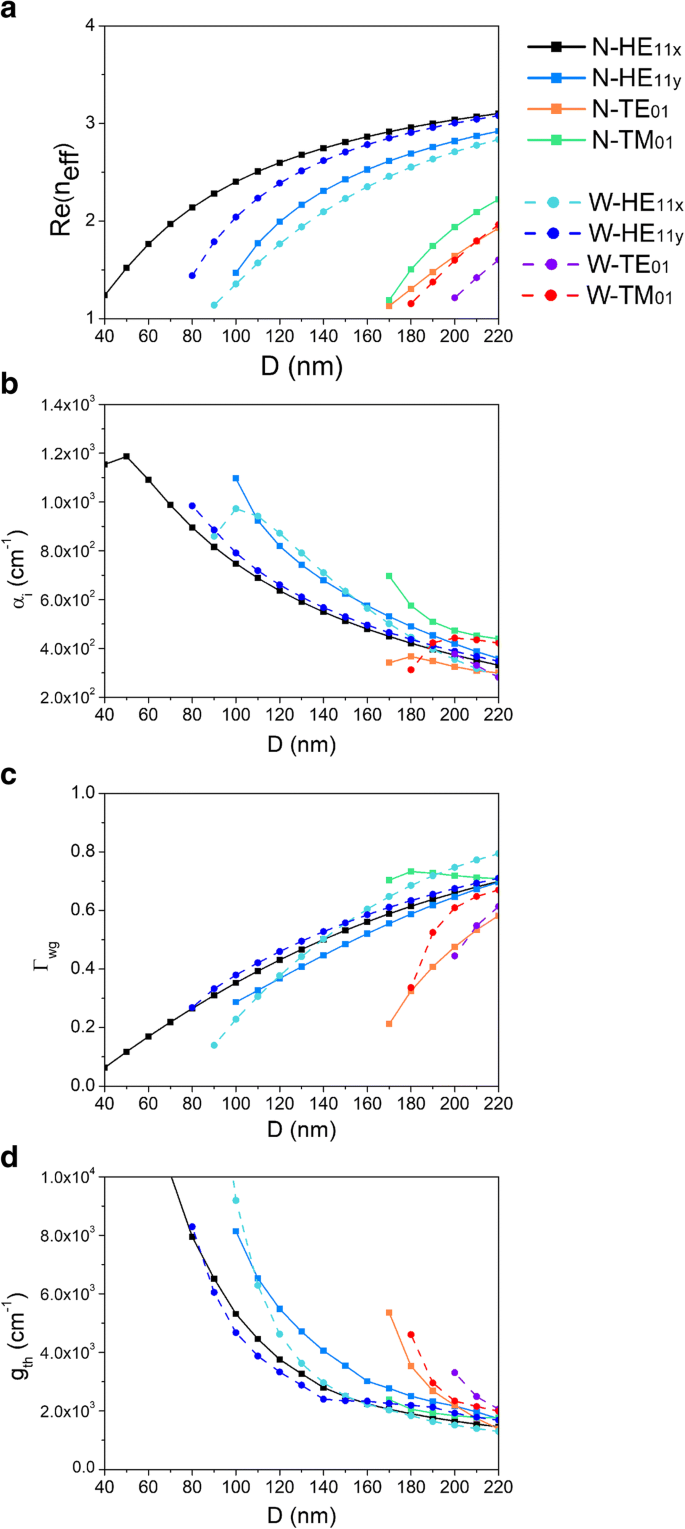
Dependências de a a parte real do índice efetivo, b perda modal, c fator de confinamento modal e d ganho de limiar no diâmetro do nanofio D

A perda modal por unidade de comprimento α _i e fator de confinamento modal Γ _wg são fatores significativos da cavidade óptica relevantes para o laser. O fator de confinamento modal é um indicador de quão bem o modo se sobrepõe ao meio de ganho, que é definido como a relação entre o ganho modal e o ganho material na região ativa [27, 28]. A perda modal por unidade de comprimento α _i pode ser obtido a partir da parte imaginária da constante de propagação modal k _z como α _i =2 Im [ k _z ] Como mostrado na Fig. 4b, a perda modal de lasers CPN-N e CPN-W se comporta negativamente correlacionada com o diâmetro do nanofio D . Considerando que, como mostrado na Fig. 4c, o fator de confinamento dos lasers CPN-N e CPN-W se comporta positivamente correlacionado com o diâmetro do nanofio D . Com a diminuição do diâmetro do nanofio, a energia eletromagnética não pode ser bem localizada dentro do nanofio, cada vez mais vazamentos de energia eletromagnética. Parte da energia eletromagnética se espalha para fora da parte superior do nanofio e parte da energia interage com a superfície do sulco levando a mais dissipação de metal. É interessante notar que o modo TM ₀₁ no CPN-N, o laser tem fator de confinamento relativamente grande e perda modal. Isso pode ser atribuído à distribuição do campo elétrico do modo TM ₀₁ . Conforme mostrado na Fig. 3d, a energia eletromagnética se distribui tanto dentro do nanofio quanto ao redor de sua superfície. Embora o confinamento seja mais rígido, a energia eletromagnética tem uma interação mais forte com a ranhura de metal. É importante ressaltar que na Fig. 4c, conforme o diâmetro do nanofio aumenta, o fator de confinamento se torna maior, indicando que a energia eletromagnética está confinada na cavidade e se sobrepõe bem à região ativa e, potencialmente, diminui o limiar de laser.

O limite de lasing é o nível de excitação mais baixo no qual a saída do laser é dominada pela emissão estimulada em vez da emissão espontânea. O ganho de limiar g _th , que descreve o ganho necessário por unidade de comprimento para lasing, é definido como \ ({g} _ {\ mathrm {th}} =\ frac {1} {\ varGamma_ {wg}} \ left [{\ alpha} _i + \ frac {1} {L} \ ln \ left (\ frac {1} {R} \ right) \ right] \), onde R denota a média geométrica da refletividade das facetas finais do nanofio e L é o comprimento da cavidade F-P do nanofio [29]. O comprimento L é fixada em 10 μm, que se encaixa nos dados experimentais na Ref. [12]. Deve-se notar que o nanofio aqui é o mesmo que a Ref. [11, 12], em que o método de crescimento do catalisador de partículas de Au foi adotado. Portanto, há uma tampa dourada no topo do nanofio. Para a faceta final com uma tampa dourada, a refletividade é maior do que a outra faceta final, atingindo cerca de e mais de 70%. Descrevemos a dependência do ganho de limiar g _th em D na Fig. 4d. É óbvio que o ganho de limiar diminui com o aumento do diâmetro do nanofio. Isso está de acordo com os comportamentos de perda modal e fator de confinamento, que são os principais fatores de ganho de limiar. Conforme o diâmetro do nanofio aumenta, a energia eletromagnética é melhor confinada dentro do nanofio, levando a um fator de confinamento maior e menor perda de vazamento de energia. Assim, o ganho do limiar torna-se mais baixo. Na faixa de diâmetro menor, o ganho de limiar do modo HE _11x é inferior ao modo HE _11y no laser CPN-N, o ganho de limiar do modo HE _11y é inferior ao modo HE _11x em laser CPN-W. Isso também prova o modo HE _11x e HE _11y gira em lasers de CPN, devido ao efeito dos ângulos de ranhura nos componentes do campo elétrico.

Fator de qualidade Q de um modo de cavidade é indicativo de quanto tempo a energia armazenada desse modo permanece na cavidade quando as transições entre bandas estão ausentes, o que está relacionado ao tempo de vida do fóton τ _p entra na equação da taxa por meio da frequência de ressonância ω do modo. Para uma cavidade F-P, o fator de qualidade é definido na seção de métodos [30]. Fator de alta qualidade indica uma baixa taxa de perda de energia em relação à energia armazenada na cavidade e as oscilações morrem lentamente. Portanto, o dispositivo pode cair em um limite inferior e, portanto, a potência da bomba pode ser reduzida. Nós retratamos Q fator como funções de D na Fig. 5a. Existem correlações positivas entre os fatores de qualidade de todos os modos e diâmetro D , exceto para os modos TM ₀₁ em lasers CPN-N e CPN-W. Isso pode ser atribuído à distribuição do campo elétrico do modo TM ₀₁ , que foi discutido acima. Além disso, a taxa de emissão espontânea em um nanolaser como o laser CPN depende parcialmente do ambiente de uma fonte de luz. De acordo com o papel de ouro de Fermi, a taxa de emissão espontânea de um emissor é proporcional à densidade local de estados ópticos (LDOS) [31]. Em um ambiente em que a estrutura está na escala do comprimento de onda, o LDOS pode ser controlado espacialmente [32]. Como resultado, o LDOS de um emissor pode ser localmente aumentado junto com a taxa de emissão espontânea ou diminuído pela microcavidade do sub comprimento de onda, que é chamado de efeito Purcell [33]. A energia eletromagnética nanolocalização pode diminuir o limite de laser, aumentando a taxa de emissão espontânea por meio do efeito Purcell. Nos lasers CPN-N e CPN-W, a energia eletromagnética está bem localizada na escala de comprimento de onda, resultando em grandes fatores de Purcell, conforme mostrado na Fig. 5b. A ranhura de metal modifica o ambiente dielétrico ao redor do nanofio e constrói uma cavidade de comprimento de onda, permitindo um volume ultrapequeno e o acoplamento entre um modo de exciton e microcavidade. Com a diminuição do diâmetro, o fator de Purcell aumenta drasticamente e chega a mais de 100. Além disso, um grande LDOS pode aumentar não apenas a taxa de emissão espontânea, mas também o processo de emissão estimulado na ação do laser. A ação de lasing poderia ser mais fácil de alcançar porque o campo eletromagnético nanolocalização do modo plasmônico híbrido não só faz com que os excitons no nanolaser se difundam rapidamente em direção a áreas de recombinação mais rápida, melhorando a sobreposição entre o ganho de material e o modo plasmônico, mas também estimula as partículas de estado excitado a transferir energia em plasmons da mesma frequência, fase e polarização. Para quantificar a escala de localização do sub comprimento de onda, a área modal normalizada calculada usando o método na Ref. [13] e apresentado na Fig. 5c. Em comparação com a Fig. 5b, o fator de Purcell é inversamente proporcional à área modal normalizada, o que prova que a cavidade na escala de comprimento de onda aumenta o fator de Purcell e, portanto, aumenta a taxa de emissão espontânea.

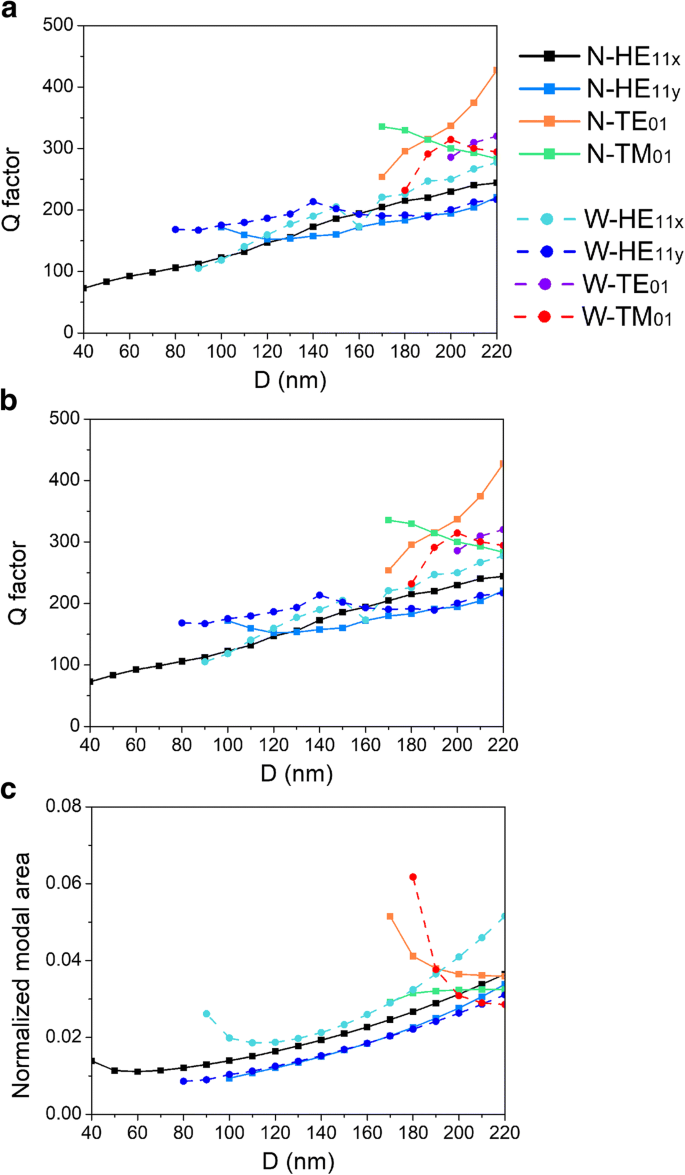
Dependências de a fator de qualidade, b Fator de Purcell e c área modal normalizada no diâmetro do nanofio D

Conclusões

Propusemos uma estrutura de laser CPN baseada em nanofio semicondutor e ranhura em V de metal juntamente com uma camada dielétrica ultrafina. Com a presença de nanofios de alto índice, plasmons de canal podem existir nas ranhuras com ângulos relativamente grandes formando modos plasmônicos de canal híbrido. A ranhura de metal modifica o ambiente dielétrico em torno do nanofio e constrói uma cavidade de comprimento de onda que permite o aumento da taxa de emissão espontânea. Propriedades guia e lasing foram investigadas usando o método dos elementos finitos. O modo fundamental HE _11x no CPN-N, o laser tem um diâmetro de corte muito pequeno, permitindo uma pegada ultrapequena de lasers no chip. Com a vantagem de alto confinamento e área modal normalizada ultrapequena, o fator de Purcell pode chegar a mais de 150 para aumentar muito a taxa de emissão espontânea. Além disso, este laser CPN também tem potencial capacidade de integração com guias de onda plasmônica usando modos CPP em guias de onda plasmônica V-groove, que encontrariam aplicações importantes em interconexões ópticas on-chip.

Métodos / Experimental

As propriedades guia e laser foram calculadas numericamente usando o método dos elementos finitos com a condição de contorno de espalhamento na frequência, que é uma abordagem comumente empregada para simular o limite aberto necessário. As distribuições de campo elétrico dos modos próprios dos lasers CPN são obtidas diretamente por análises de modo. As propriedades de orientação são calculadas pela constante de propagação complexa com β + iα . A parte real do índice modal efetivo é calculada por n _eff =Re ( n _eff ) = β / k ₀ , onde k ₀ é o vetor de onda do vácuo. A área de modo efetiva é calculada usando [24]
$$ {A} _m =\ frac {W_m} {\ max \ left \ {W (r) \ right \}} =\ frac {1} {\ max \ left \ {W (r) \ right \}} {\ iint} _ {\ infty} W (r) {d} ^ 2r $$ (1)
onde W _m é a energia total do modo e W (r) é a densidade de energia (por unidade de comprimento fluida ao longo da direção de propagação). Para materiais dispersivos e com perdas, o W (r) dentro pode ser calculado usando a Eq. (2):
$$ W (r) =\ frac {1} {2} \ left (\ frac {d \ left (\ varepsilon (r) \ omega \ right)} {d \ omega} {\ left | E (r) \ direita |} ^ 2 + {\ mu} _0 {\ left | H (r) \ right |} ^ 2 \ right) $$ (2)
Fator de qualidade e Purcell são definidos como [30, 33]
$$ \ kern0.75em \ frac {1} {Q} =\ frac {1} {{\ omega \ tau} _p} =\ frac {\ nu_ {g, z} \ left (\ omega \ right)} { \ omega} \ left [{\ alpha} _i + \ frac {1} {L} \ ln \ left (\ frac {1} {R} \ right) \ right] $$ (3) $$ {F} _p =\ frac {3} {4 {\ pi} ^ 2} {\ left (\ frac {\ lambda} {n} \ right)} ^ 3 \ left (\ frac {Q} {V_ {eff}} \ right) $$ (4)
Equações para calcular a perda modal, fator de confinamento modal e ganho de limiar são fornecidas no texto principal; não narramos aqui novamente.

Abreviações

CPN:: Nanofio de plasmon de canal
CPN-N:: Canal de plasma nanofio de ângulo estreito
CPN-W:: Grande angular de nanofio de plasmon de canal
CPP:: Canal plasmon-polariton

Imersão potencial em fotovoltaicos orgânicos sondados por microscopia de força de sonda Kelvin transversal Efeitos das variações de gravação na formação do canal Ge / Si e desempenho do dispositivo

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias