Ressonância Fano High-Q na frequência Terahertz baseada em um ressonador de metamaterial assimétrico
Resumo
Nós propomos um metamaterial plano formado por ressonadores metálicos de quatro tiras, que podem alcançar alto Q Ressonância de Fano em regime de terahertz. Este metamaterial planar terahertz suporta uma ressonância Fano nítida em 0,81 THz com transmissão de 25%. A largura de banda de ressonância do mergulho é 0,014 THz com o Q -fator de 58. A interferência entre o modo claro e o modo escuro leva ao formato da linha Fano. Este perfil acentuado de Fano é explicado pela teoria eletromagnética da ressonância de Fano. Além disso, várias ressonâncias Fano podem ser realizadas adicionando mais tiras na estrutura original. Como exemplo, dois mergulhos Fano com Q - fatores de 61 e 65 podem ser obtidos por meio de uma estrutura de cinco tiras.
Histórico
Metamaterial é um tipo de material artificial que exibe propriedades exóticas, como índice de refração negativo [1] e índice de refração ultra-alto [2], que não pode ser realizado por materiais naturais na maioria das situações. Esse material artificial é composto por uma grande quantidade de unidades metálicas periódicas e suas características (por exemplo, permissividade e permeabilidade) podem ser facilmente controladas alterando os parâmetros geométricos das unidades [3]. Como resultado, o estudo de metamateriais atraiu grande atenção nos últimos anos. Muitas novas aplicações surgiram neste domínio, incluindo absorção perfeita [4, 5], sensores de metamaterial [6,7,8,9], cloaking [10], efeitos de Fano [11], etc.
A forma da linha da ressonância de Fano é bastante diferente do perfil simétrico de Lorentz. É assimétrico e nítido com um Q relativamente alto -fator. Uma vez que Fano revelou teoricamente o mecanismo quântico da ressonância de Fano [12], tornou-se um tópico quente. Para ilustrar a origem da ressonância de Fano, várias teorias foram estabelecidas, incluindo a análise mecânica quântica de Fano [12], o modelo clássico do oscilador [13], a teoria do modo acoplado [14] e a teoria eletromagnética da ressonância de Fano [15, 16] . De acordo com a teoria eletromagnética da ressonância de Fano proposta por Gallinet e Martin [16], o perfil distinto de Fano é atribuído ao acoplamento entre um modo não radiativo e um modo radiativo que também pode ser visto como um continuum.
No regime de terahertz, a ressonância de Fano nítida pode ser alcançada pela introdução de uma assimetria fraca nos metamateriais [17,18,19,20], o que pode levar ao aparecimento de um modo escuro subjacente [21]. Além disso, materiais de grafeno também podem ser utilizados para gerar e até modular a ressonância de Fano [22, 23]. Comparado com a maioria de EIT (transparência induzida eletromagneticamente) [24, 25] e PIT (transparência induzida por plasmon) [26, 27], o formato da linha de Fano é muito mais nítido e estreito. O Q -fator do perfil de Fano [17, 28] é aproximadamente dez vezes maior do que a forma da linha Lorentziana [29,30,31] em muitas situações. Esta propriedade torna a ressonância de Fano uma escolha promissora para realizar a detecção sensível [8]. No entanto, o Q -fator de muitos metamateriais não é alto o suficiente [17, 32, 33], o que limita suas aplicações em termos de detecção. A fim de aplicar ampla e eficientemente a ressonância Fano na detecção, é uma tarefa necessária melhorar muito o Q -fator de uma metassuperfície.
Recentemente, algumas estruturas de metamateriais foram projetadas para realizar um alto Q Ressonância de Fano. Por exemplo, Ding et al. propôs um metamaterial de bicamada que consiste em dois conjuntos de anéis de divisão assimétricos com diferentes parâmetros geométricos. Pode suportar três ressonâncias Fano cujas Q -fatores são, respectivamente, 33, 42 e 25 [19]. Uma estrutura de dímero simétrica composta de ressonadores de anel cuspidor idênticos em cada camada também foi apresentada para melhorar seu Q -fator [34]. No entanto, essas estruturas empilhadas estão sofrendo de desafios técnicos na fabricação. Alto- Q a ressonância com um design de estrutura simples ainda é uma questão importante.
Neste artigo, demonstramos uma estrutura de metamaterial coplanar composta por quatro tiras metálicas. Em cada célula unitária, três faixas paralelas são dispostas perpendicularmente à quarta. Esta estrutura pode suportar um alto Q Ressonância Fano ( Q -valor é cerca de 58) em 0,81 THz com transmissão de 25%. Esta forma de linha nítida se origina da interação entre o modo claro (radiativo) e o modo escuro (não radiativo). Para uma discussão mais aprofundada, a teoria eletromagnética da ressonância de Fano é empregada [15, 16]. As propriedades da ressonância de Fano podem ser alteradas por meio do controle de parâmetros geométricos. O desempenho de detecção do dispositivo é discutido. Além disso, ao adicionar mais tiras à estrutura projetada originalmente, várias ressonâncias Fano podem ser realizadas.
Métodos / Experimental
Uma grande quantidade de pesquisas indica que romper a simetria de uma estrutura pode induzir uma forma de linha de Fano assimétrica [17, 18, 35,36,37]. Com base neste conceito, projetamos este metamaterial de quatro tiras exibido na Fig. 1, onde a tira 2 é definida para realizar uma quebra de simetria. A Figura 1a mostra o diagrama tridimensional do metamaterial proposto. A Figura 1b, c mostra respectivamente a vista lateral e a vista superior da unidade de estrutura. Os ressonadores metálicos de quatro tiras são colocados no topo de um substrato dielétrico ideal cuja parte real do índice de refração é 1,5 e a parte imaginária é 0. Na realidade, este material dielétrico é correspondente à sílica. Ou seja, o substrato é sem perdas na região de terahertz. Escolhemos Au com condutividade σ =4,09 × 10 7 S / m para formar o ressonador planar metálico cuja espessura é de 0,2 μm. O período de repetição é P x = P y =180 μm. Três tiras paralelas (1, 2 e 3) têm o mesmo tamanho. Seu comprimento é l x =120 μm e a largura é w =20 μm. A faixa 4 é perpendicular às outras faixas (1, 2 e 3). Seu comprimento é l y =150 μm e a largura é w =20 μm. A distância entre o eixo da faixa 2 e o ponto central da estrutura é d =30 μm. O método de diferença finita no domínio do tempo é usado para simular este metamaterial planar. A fim de economizar tempo de simulação e memória de computação, escolhemos os tamanhos de malha de Δ x =Δ y =1 μm e Δ z =0,02 μm. Nós achamos que os resultados da simulação são bastante precisos neste caso. Mesmo que tamanhos de malha menores sejam aplicados, os resultados da simulação permanecem quase inalterados. As condições de contorno de simulação ao longo de x -eixo e y -eixos são definidos como periódicos, e a condição ao longo de z -eixo é definido como camadas perfeitamente combinadas. A Figura 1a mostra que toda a estrutura é iluminada por um feixe de onda THz normalmente incidente. Como pode ser visto na Fig. 1b, c, o vetor elétrico E e vetor magnético H do feixe THz incidente são y -eixo polarizado e x -eixo polarizado, respectivamente.
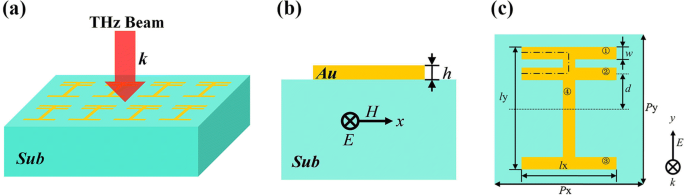
Diagrama tridimensional do metamaterial proposto ( a ) Vista lateral ( b ) e vista superior ( c ) do ressonador metamaterial assimétrico; o comprimento equivalente l é marcado por linha ponto-traço
Resultados e discussão
O espectro de transmissão da metassuperfície proposta é mostrado na Fig. 2a. Há duas quedas de transmissão nas frequências de 0,430 THz e 0,809 THz com taxas de transmissão de 0,10% e 26,45%, respectivamente. Para tornar a explicação a seguir mais concisa, usamos R s R s e R d para marcar esses dois modos ressonantes, R s para o modo ressonante em 0,430 THz e R d para o modo ressonante em uma frequência mais alta. A taxa de transmissão óptica de R s mostra um perfil de Lorentz simétrico com uma largura de banda relativamente ampla de 0,256 THz. Em comparação, R d exibe uma forma de linha Fano assimétrica que é muito mais nítida com uma largura de banda de 0,014 THz. Q -fator é um critério importante para julgar a forma da linha. Pode ser obtido dividindo a frequência central pela largura de banda. Na verdade, o Q -fator de R d pode chegar a 58, 30 vezes mais que o Q -valor de R s , o que contribui para aplicativos subjacentes em muitos campos. A existência do perfil de Fano assimétrico enraíza-se na interação entre um modo escuro e um modo claro, ou seja, a interação entre um estado não radiativo e um contínuo, gera a partir de um estado radiativo [16, 38, 39]. No resto do artigo, o mecanismo detalhado da forma da linha de Fano será discutido e os espectros de transmissão teóricos serão analisados. Embora a transmissão em 0,809 THz seja de 26,45% na metassuperfície proposta, ela pode ser reduzida ainda mais. De acordo com [40, 41], a utilização de materiais dielétricos com perdas pode reduzir a transmissão. Em nossas simulações, o material de substrato que escolhemos é um material ideal com um índice de refração real de 1,5 que não tem perda na região de terahertz. Um método viável para reduzir a transmissão é usar um material com perdas com um índice de refração complexo para formar o substrato, em vez deste material sem perdas ideal.
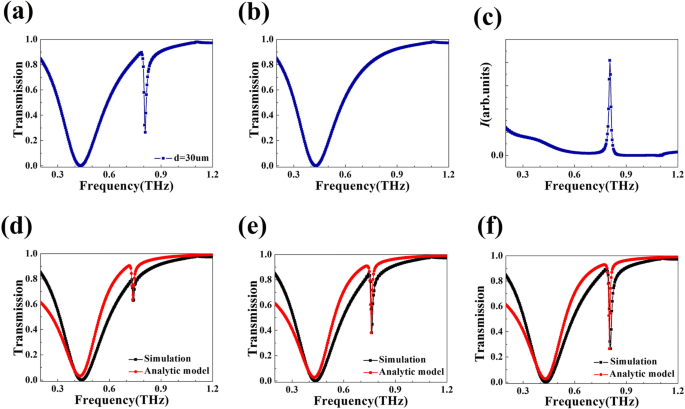
a Curva de transmitância da metassuperfície projetada dada por simulação numérica. b Espectro de transmissão do modo brilhante. c Intensidade de campo da nanoestrutura de quatro tiras proposta iluminada por uma fonte dipolo. d , e , f Espectro de transmissão simulado (curva vermelha) e teórico (curva preta) da estrutura projetada com d =10 μm, d =20 μm e d =30 μm, respectivamente
A fim de descobrir a origem da curva de transmitância, a distribuição do campo elétrico ∣ E ∣ e o z componente do campo magnético ( H Z ) na frequência central de dois mergulhos ressonantes são dados na Fig. 3. Podemos encontrar grandes diferenças entre as distribuições de campo de R s e R d . A Figura 3a indica que o campo elétrico do modo ressonante R s concentra-se principalmente nas tiras 1 e 3, especialmente nas extremidades dessas duas tiras. No entanto, há muito pouca distribuição de campo elétrico em outras partes da estrutura, incluindo a faixa 2 e a faixa 4. Essa distribuição de campo elétrico é devido ao campo eletromagnético da luz normalmente incidente cujo vetor elétrico E está junto com y -eixo. Portanto, R s pode ser considerada como ressonância fundamental (isto é, resposta eletromagnética EM (eletromagnética) localizada) [42]. Além disso, a distribuição do z componente do campo magnético ( H Z ) para o modo R s é mostrado na Fig. 3b, a partir da qual podemos obter a distribuição da corrente de superfície. Foi demonstrado que a análise da corrente de superfície pode servir como um método vital para revelar como o acoplamento de modos gera a ressonância de Fano [28]. Conforme mostrado na Fig. 3b, a corrente de superfície flui da parte inferior para a parte superior da estrutura, contribuindo para a coleta de cargas opostas em ambos os lados da faixa 1 e da faixa 3. Em contraste, a distribuição do campo na frequência central de R d é bastante diferente. O campo elétrico intenso é encontrado ao redor das faixas 1 e 2 (Fig. 3c), que é aproximadamente quatro vezes maior do que o modo R s . De acordo com a distribuição de H Z campo mostrado na Fig. 3d, é claro que a corrente de superfície flui para cima entre a faixa 1 e a faixa 2, enquanto a corrente entre a faixa 2 e a faixa 3 flui de forma oposta. No nível macro, tal distribuição de campo pode ser vista como algum tipo de indução de carga entre as faixas horizontais. Do ponto de vista do acoplamento de modo, esse fenômeno se deve à interação entre o modo claro e o modo escuro.
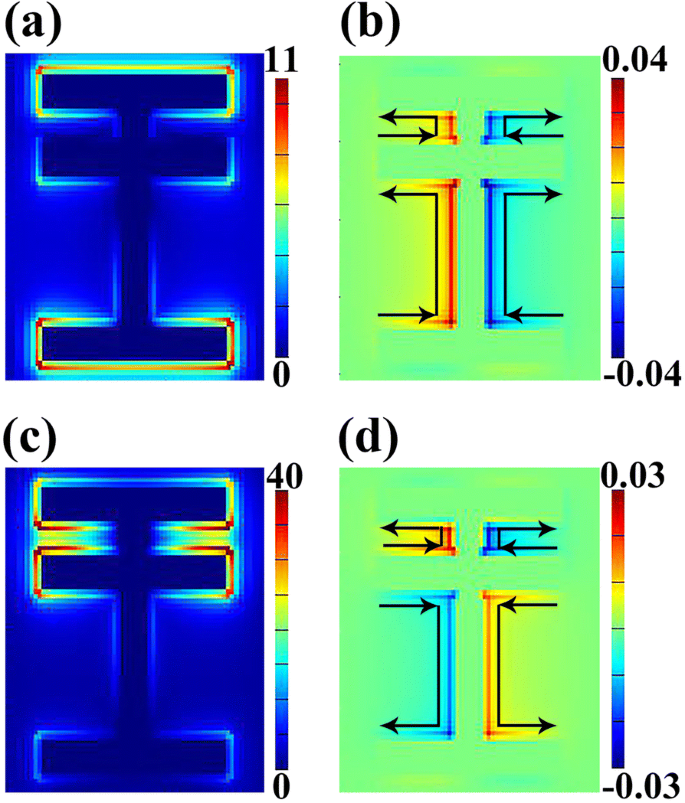
Distribuições de campo elétrico ∣E∣ ( a ) e z componente do campo magnético (H Z ) ( b ) a 0,430 THz ( R s ); distribuições de ∣E∣ ( c ) e H Z ( d ) a 0,809 THz ( R d ); setas pretas em b e d representam a direção da corrente de superfície
Com o objetivo de aprofundar e quantificar nossa explicação, os espectros de modo claro e modo escuro são simulados e a teoria eletromagnética de ressonância de Fano [15, 16] é utilizada na estrutura proposta. A Figura 2b mostra o espectro de transmissão de uma estrutura cuja unidade periódica consiste nas faixas 1, 3 e 4. O modo ressonante suportado por tal estrutura pode ser excitado diretamente por uma onda plana; portanto, é o "modo claro". Em contraste, um modo escuro não pode ser excitado por um feixe de onda plana; pode ser excitado através de um campo que varia rapidamente, por exemplo, o campo próximo de um dipolo [15, 43]. A Figura 2c exibe a intensidade do campo do metamaterial de quatro tiras iluminado por uma fonte dipolo [44]. As equações de Maxwell formam uma base sólida da teoria eletromagnética da ressonância de Fano em nanoestruturas. De acordo com as equações de Maxwell, vetor elétrico E obedece a equação de onda abaixo:
$$ {\ in} ^ {- 1} \ left (\ mathbf {r}, \ upomega \ right) \ nabla \ times \ nabla \ times \ mathbf {E} \ left (\ mathbf {r}, \ upomega \ direita) - \ frac {\ upomega ^ 2} {{\ mathrm {c}} ^ 2} \ mathbf {E} \ left (\ mathbf {r}, \ upomega \ right) =0 $$ (1)
onde ω é a frequência do feixe incidente e ∈ ( r , Ω) é a constante dielétrica complexa do material com perdas. O campo elétrico E e a permissividade ∈ estão ambas relacionadas com a frequência ω assim como com o vetor posição r . Dois operadores de projeção ortogonal P e Q podem ser usados para separar a função de onda ∣ E > em um modo claro P ∣ E > e um modo escuro Q ∣ E >, ou seja, um modo radiativo e um modo não radiativo [15, 38]. Por meio de derivação complicada, a razão entre a intensidade do campo total e a intensidade do modo brilhante pode ser dada como
$$ {I} _ {\ mathrm {a}} \ left (\ upomega \ right) =\ frac {{\ left (\ frac {\ upomega ^ 2 - {\ upomega _ {\ mathrm {a}}} ^ 2 } {2 {W} _ {\ mathrm {a}} {\ upomega} _ {\ mathrm {a}}} + q \ right)} ^ 2 + b} {{\ left (\ frac {\ upomega ^ 2 - {\ upomega _ {\ mathrm {a}}} ^ 2} {2 {W} _ {\ mathrm {a}} {\ upomega} _ {\ mathrm {a}}} \ right)} ^ 2 + 1} $$ (2)
onde W a e ω a são a largura de banda e a frequência central da ressonância assimétrica, respectivamente. O parâmetro assimétrico q e o parâmetro de amortecimento da modulação b são indispensáveis para descrever eu a (ω) [15, 16]. A Eq. (2) sugere que eu a (ω) exibe um perfil assimétrico, que finalmente resulta na forma da linha de Fano assimétrica na curva de transmitância.
A intensidade do modo de brilho R s segue um perfil suave de Lorentz. Depende da frequência ω e obedece à seguinte equação:
$$ {I} _ {\ mathrm {s}} \ left (\ upomega \ right) =\ frac {a ^ 2} {{\ left (\ frac {\ omega ^ 2 - {\ omega _ {\ mathrm {s }}} ^ 2} {2 {W} _ {\ mathrm {s}} {\ omega} _ {\ mathrm {s}}} \ right)} ^ 2 + 1} $$ (3)
dos quais W s e ω s são, respectivamente, a largura de banda e a frequência central do espectro exibido na Fig. 2b, e a é o valor máximo da amplitude da ressonância. A força total eu ( ω ) da ressonância pode ser calculada pelo produto de I a e eu s , a partir do qual podemos finalmente obter a transmitância T (ω).
$$ I \ left (\ omega \ right) ={I} _ {\ mathrm {a}} \ left (\ omega \ right) \ times {I} _ {\ mathrm {s}} \ left (\ omega \ direita) $$ (4) $$ T \ left (\ omega \ right) =1-I \ left (\ omega \ right) $$ (5)
A fim de atender ao requisito de conservação de energia, a não deve ser maior que 1. W a e ω a pode ser calculado a partir da frequência central e largura de banda [15, 16]. O parâmetro assimétrico q bem como o parâmetro de amortecimento de modulação b pode ser obtido através do método dado por [16]. Dessa forma, podemos obter o espectro de transmissão teórico dessa estrutura assimétrica. Na Fig. 2f, a curva preta representa o espectro de transmissão dado pelo método FDTD e a curva vermelha fornece os resultados do nosso cálculo baseado na teoria eletromagnética da ressonância de Fano. A tendência consistente da curva preta e vermelha indica que é razoável atribuir as características de transmissão do ressonador ao acoplamento do modo claro e modo escuro. Esta conclusão também coincide com a distribuição do campo na Fig. 3.
O parâmetro geométrico d descreve a distância entre o eixo da faixa 2 e o ponto central de toda a estrutura (Fig. 1c). Isso pode afetar muito a frequência central de quedas de transmissão, bem como seus coeficientes de transmissão. Espectros de transmissão correspondentes com d diferentes são mostrados na Fig. 2d, e. A curva preta e a curva vermelha representam o espectro de transmissão baseado em simulação e cálculo teórico, respectivamente. Com d mudando de 10 para 30 μm, é claro que uma queda acentuada de Fano se aprofunda, resultante da força de acoplamento crescente entre o modo claro e o modo escuro. Além disso, a frequência central do modo R d existe um deslocamento distinto para o azul quando a faixa 2 é colocada mais perto da faixa 1. Com base no modelo do circuito LC, a frequência de ressonância de R d é dado por [45].
$$ {\ omega} _ {\ mathrm {d}} =\ frac {1} {2 \ uppi \ sqrt {\ mathrm {LC} / 2}} \ propto \ frac {1} {\ mathrm {l}} $$ (6)
onde l é o comprimento equivalente do ressonador correspondente. A equação (6) indica que a frequência central ω d está em proporção inversa a l . Em nossa estrutura, comprimento equivalente l é indicado pelo comprimento da linha ponto-traço na Fig. 1c. Isso ocorre porque as distribuições de campo de R d são principalmente restritos às tiras 1 e 2. O comprimento da tira 1 (e 2) e a distância entre as duas tiras juntas decidem l. Quando d aumenta, a distância entre as duas faixas diminui. Portanto, como mostrado na Fig. 1c, o comprimento equivalente diminui quando d muda de 10 para 30 μm. Isso leva ao aumento de R d Frequência de ressonância.
De acordo com a teoria da ressonância de Fano sugerida por Fano em 1961 [12], o processo de autoionização é estudado e a forma assimétrica da linha de ressonância é atribuída à interferência entre um continuum e um estado discreto. Essa também é a origem das características assimétricas do ressonador metamaterial apresentadas neste artigo. Conforme mostrado na Fig. 4, um sistema de três níveis pode ser utilizado para esclarecer o mecanismo de transição da estrutura. R 0 serve como o estado fundamental de todo o sistema. Modo brilhante R 1 é um modo radiativo que pode ser excitado diretamente pelo feixe normalmente incidente. Neste sistema, o estado não radiativo R 2 pode ser considerado como um “modo escuro” [21], conforme discutido anteriormente. R 2 pode ser excitado através da quebra de simetria. A introdução de uma assimetria oferece um canal para permitir que o modo claro se acople ao modo escuro e, portanto, leva à ressonância de Fano [46].
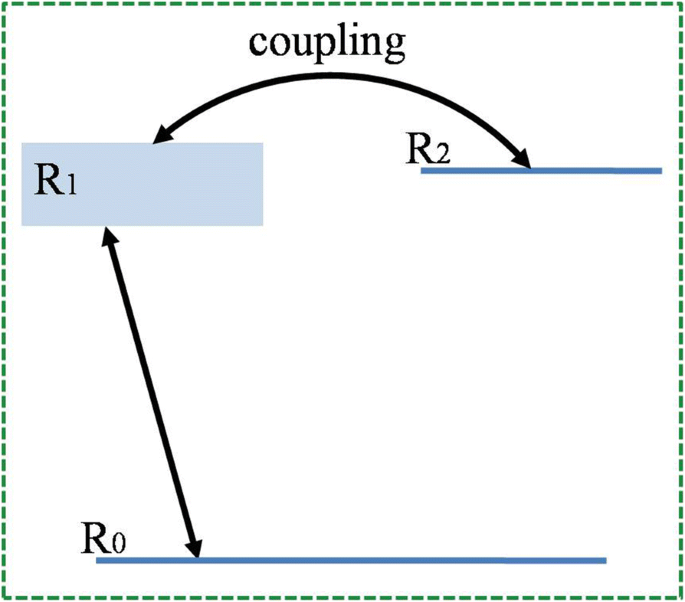
Diagrama esquemático do sistema de três níveis
A forte interação entre a onda eletromagnética incidente e a camada de analito torna alto- Q Fano ressonância, um método promissor para realizar a detecção ultrassensível do índice de refração n [8]. O dispositivo proposto na Fig. 5a pode funcionar como um sensor eficaz para detectar o índice de refração n da camada de analito no topo, cuja espessura é de 4 μm. A frequência central do mergulho Fano mudará com a mudança de n . Portanto, podemos obter o índice de refração analisando a frequência ressonante de R d . A Figura 5b mostra o deslocamento da frequência ressonante do mergulho Fano no dispositivo. Um distinto deslocamento para o vermelho aparece quando n é aumentado de 1 para 1,6. A sensibilidade do sensor S é igual a \ (\ frac {\ varDelta f} {\ varDelta n} \). Aqui, S do sensor é calculado como 0,105 THz / RIU (unidade de índice de refração). É bem sabido que FOM (Figura de mérito) é um critério vital para o desempenho de um sensor [47]. Pode ser calculado por FOM =\ (\ frac {S} {\ mathrm {linewidth}} \). Nessa estrutura apresentada, o valor do FOM pode chegar a 7.501, que está em um nível ideal [47, 48]. A capacidade de detecção também é geralmente discutida por FOM * =\ (\ frac {S ^ {\ ast}} {I} \) e S * =\ (\ frac {\ varDelta I} {\ varDelta n} \), que está relacionado à intensidade detectada. O resultado do cálculo de S * nesta estrutura é 2,6 / RIU. E o FOM * em nossa estrutura é calculado em 10. Também fizemos alguns trabalhos para descobrir a variação da resposta com a espessura da camada de analito. Consulte o arquivo adicional 1.
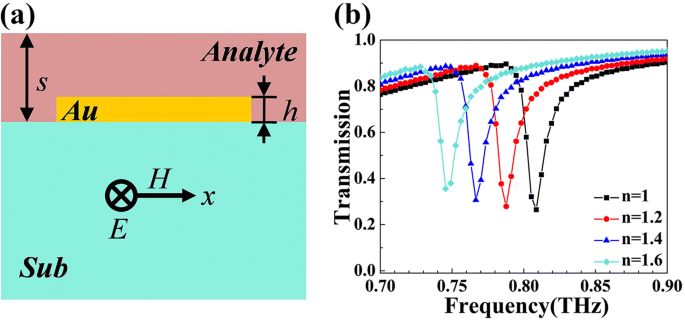
a Seção transversal do dispositivo de detecção. b Dependência do espectro de transmissão nas mudanças do índice de refração n
Múltiplas ressonâncias Fano podem ter aplicações em muitas situações. No entanto, a maioria dos metamateriais Fano plasmônicos são projetados para suportar ressonância Fano única [11, 17]. Portanto, não é fácil para eles perceberem múltiplas ressonâncias de Fano por meio do ajuste da estrutura. Neste artigo, percebemos várias ressonâncias de Fano adicionando mais tiras horizontais ao design original do metamaterial. Apresentamos uma estrutura de cinco tiras como um exemplo representativo. O diagrama esquemático do ressonador de cinco tiras é mostrado na Fig. 6a. As tiras 1, 2, 3 e 4 são do mesmo tamanho e paralelas entre si. Seu comprimento é l x =120 μm e a largura é w =20 μm. Faixa 3 está localizada no meio, e a distância d entre os eixos da faixa 2 e da faixa 3 é de 32 μm. A faixa 5 é perpendicular às outras quatro faixas. Seu comprimento é l y =150 μm e a largura é w =20 μm. As condições de contorno e o tamanho da malha são mantidos os mesmos da simulação do ressonador de quatro faixas. O resultado da simulação é mostrado na Fig. 6b, na qual podemos encontrar claramente duas quedas acentuadas de Fano em 0,75 THz e 0,91 THz. O Q os valores desses dois mergulhos são, respectivamente, 61 e 65. Mais mergulhos Fano devem ser gerados se mais tiras horizontais forem adicionadas à estrutura.
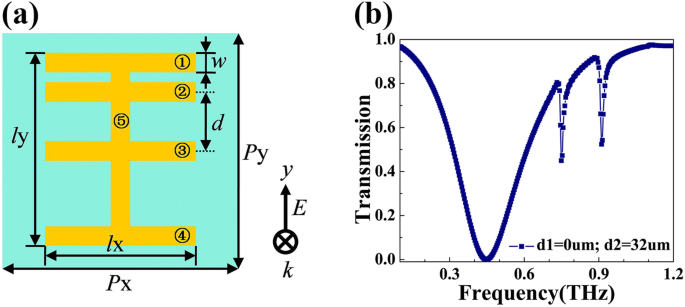
a Vista superior da estrutura de cinco tiras proposta. b Curva de transmitância simulada do ressonador de cinco faixas
Conclusão
Em conclusão, projetamos um ressonador plano de quatro faixas que pode suportar ressonância Fano nítida com um alto Q -valor. A largura de banda do mergulho Fano é 0,014 THz e seu Q -fator é 58. A interação entre o modo claro e o modo escuro resulta no aparecimento do perfil Fano assimétrico. O espectro de transmissão teórico é calculado neste artigo. Além disso, vários altos- Q As ressonâncias de Fano podem ser realizadas adicionando-se mais faixas horizontais à estrutura. Esta estrutura pode ser aplicada em sensores e outros campos.
Abreviações
- EIT:
-
Transparência induzida eletromagneticamente
- EM:
-
Eletromagnética
- FOM:
-
Figura de mérito
- PIT:
-
Transparência induzida por plasma
- Q :
-
Fator de qualidade
- RIU:
-
Unidade de índice de refração
Nanomateriais
- Aplicações de Ressonância
- Nano grafema, memória transparente flexível à base de silício
- Nanobiossensor de ouro com base na ressonância de plasma de superfície localizada é capaz de diagnosticar a brucelose humana, apresentando um método rápido e acessível
- Sensor plasmônico baseado em nanoprismas dielétricos
- Gerando e manipulando fatores de alta qualidade de ressonância de Fano no ressonador Nanoring por empilhamento de meio Nanoring
- Estimativa do armazenamento de energia do supercapacitor com base em equações diferenciais fracionais
- Fotodetector controlado por comprimento de onda baseado em nanobelt de CdSSe único
- Metassuperfícies plasmônicas opticamente ativas com base na hibridização de acoplamento In-Plane e Out-of-Plane Coupling
- Projeto de um absorvedor Terahertz de banda ultralarga ajustável com base em múltiplas camadas de fitas de grafeno
- Projeto de absorvedor de metamaterial Terahertz Quad-Band usando um ressonador retangular perfurado para aplicações de detecção



