Estimativa do armazenamento de energia do supercapacitor com base em equações diferenciais fracionais

Resumo

Neste artigo, são apresentados novos resultados sobre o uso apenas de medições de tensão em terminais de supercapacitores para estimativa de energia acumulada. Para tanto, é realizado um estudo baseado na aplicação de modelos de ordem fracionária de circuitos de carga / descarga de supercapacitores. Estimativas de parâmetros dos modelos são então usadas para avaliar a quantidade de energia acumulada no supercapacitor. Os resultados obtidos são comparados com a energia determinada experimentalmente pela medição da tensão e da corrente nos terminais do supercapacitor. Todos os testes são repetidos para várias formas e parâmetros de sinal de entrada. A consistência muito alta entre os resultados estimados e experimentais confirma completamente a adequação da abordagem proposta e, portanto, a aplicabilidade do cálculo fracionário à modelagem do armazenamento de energia do supercapacitor.

Histórico

A partir de hoje, os supercapacitores são os principais componentes de muitos dispositivos e sistemas, por exemplo, sistemas de backup de energia e recuperação de eletricidade, bem como aplicações automotivas, veículos híbridos e muitos outros. A capacidade de acumular carga sem quaisquer reações químicas faz com que tais elementos tenham um número centenas de vezes maior de ciclos de carga / descarga em comparação com baterias típicas [1]. Além disso, altas taxas de carga / descarga os tornam eficazes para aplicações em sistemas de recuperação de energia usados, por exemplo, em transporte ou fontes de energia renováveis [2, 3]. Em todas essas aplicações, o parâmetro-chave é a informação sobre a quantidade de energia acumulada no supercapacitor [4, 5]. Infelizmente, a relação bem conhecida para capacitores típicos que permite determinar a informação, ou seja, (1/2) C U ² , não pode ser usado [6]. A quantidade de energia acumulada não pode ser determinada com base na tensão nos terminais do capacitor apenas. A principal razão para isso é o processo de difusão associado à redistribuição de carga [1, 7]. É por isso que muitos pesquisadores têm tentado determinar um modelo de supercapacitor que permitisse estimar o comportamento de um sistema real. Atualmente, os pesquisadores adotam principalmente as combinações de elementos eletrônicos típicos, por exemplo, RC quadripolo ou série e combinações paralelas de tais elementos. No entanto, todos esses modelos assumem uma relação entre a corrente do supercapacitor e a tensão em seu terminal na forma de uma equação diferencial típica de ordem inteira [3–5, 7].

Mas acontece que algumas possibilidades completamente novas para estimativa de energia em tais sistemas podem ser obtidas pela aplicação do cálculo fracionário [8, 9]. O cálculo difere-integral de ordem não-inteira foi proposto há mais de 300 anos, mas questões importantes de implementação estão relacionadas com o advento dos computadores e seu uso na modelagem de sistemas dinâmicos de tempo discreto [10-14]. A aplicação do cálculo fracionário ao problema de estimativa dos parâmetros do supercapacitor não é uma questão nova. Existem muitas publicações neste campo [15–25]. Os autores realizam a tarefa de estimar parâmetros nos domínios da frequência e do tempo [26].

Este artigo é uma versão estendida da apresentação da conferência do autor [27], na qual uma abordagem de ordem fracionária foi brevemente introduzida para estimar a energia acumulada no supercapacitor.

A estimativa precisa dos parâmetros dos supercondensadores também é de extrema importância na avaliação de sua confiabilidade [28-31]. Os processos de degradação permanente dentro do supercapacitor podem alterar a resistência e a capacitância em série equivalente. Assim, a determinação precisa desses parâmetros, com base no método proposto, também permite avaliar com precisão o desempenho do capacitor.

Este artigo começa com algumas preliminares relacionadas à integração e diferenciação de ordem fracionária. A seguir, apresenta o método de estimativa de parâmetros usado durante os testes e propõe um novo método de cálculo de energia baseado no cálculo fracionário. A seção Resultados e Discussão apresentam a energia calculada para vários cenários e os compara com os valores de referência (medidos). As conclusões e contribuições estão resumidas na seção Conclusões.

Métodos

O uso de materiais porosos em supercapacitores e a forma específica de acumulação de carga fazem com que as abordagens tradicionais baseadas em modelos derivados de ordem inteira não sejam suficientemente precisas. Muitos pesquisadores propuseram várias soluções na forma de combinação de RC típicos elementos com valores constantes ou variáveis [4, 7]. Mas verifica-se que definitivamente melhor precisão pode ser obtida usando cálculo diferencial de ordem não-inteira para definir as relações entre a corrente e a tensão do supercapacitor [17, 19]. Além disso, tal solução pode resultar em uma estrutura de modelo muito simples, enquanto fornece uma precisão muito alta [18].

Cálculo diferencial-integral de ordem fracional

O cálculo diferencial de ordem fracionária é conhecido há mais de 300 anos. No entanto, apenas alguns anos recentes trouxeram sua popularidade na modelagem de fenômenos e processos físicos. Acredita-se que a descrição da dinâmica com uma derivada ou integral de ordem não-inteira pode ser um dos métodos mais eficazes para modelagem de propriedades reais de muitos fenômenos complexos e processos industriais, especialmente com base em novos materiais e tecnologias [10, 12, 13 , 32–34].

Diferencial de ordem não-inteira ou cálculo integral é uma generalização do cálculo clássico para ordem α que pertence ao conjunto de números reais \ (\ mathcal {R} \). O operador diferencial integral de ordem \ (\ alpha \ in \ mathcal {R} \) da função f ( t ) no intervalo [ a , t ] pode ser escrito da seguinte forma
$$ {{} _ {a} \ mathcal {D} _ {\ textit t} ^ {\ alpha}} f (t) =\ left \ {{\ begin {array} {lcl} {\ frac {\ mathrm {d} ^ {\ alpha} \ textit {f (t)}} {\ mathrm {d} \ textit {t} ^ {\ alpha}}} &\ text {para} &\ alpha> 0 \\ f ( t) &\ text {for} &\ alpha =0 \\ \ int_ {a} ^ {t} f (\ tau) \ textrm {d} {\ tau ^ {\ alpha}} &\ textrm {for} &\ alpha <0, \\ \ end {array}} \ right. $$ (1)
assumindo que a função f ( t ) é várias vezes diferenciável e integrável. Quanto ao operador (1), existem muitas definições para sua realização. Essas definições diferem nas propriedades e áreas de aplicação. As mais populares são as definições de Riemann – Liouville, Caputo e Grünwald – Letnikov (GL) [34]. Este último será usado neste artigo no formulário
$$ {} _ {a} \ mathcal {D} _ {t} ^ {\ alpha} f (t) ={\ lim} _ {h \ to 0} \ frac {1} {h ^ {\ alpha} } \ sum \ limits_ {j =0} ^ {\ left [{\ frac {t} {h}} \ right]} (- 1) ^ {j} {\ alpha \ choose j} f (t-jh) , $$ (2)
onde o binômio \ (\ alpha \ choose j \) é definido como segue
$$ {\ alpha \ choose j} =\ left \ {\ begin {array} {lll} 1 &\ textup {for} &j =0 \\ \ frac {\ alpha (\ alpha-1) \ dots (\ alpha -j + 1)} {j!} &\ text {para} &j> 0. \ end {array} \ right. $$ (3)
A fim de obter um modelo fracionário em momentos discretos de tempo, a definição de GL em uma forma discreta é simplificada como
$$ \ Delta_ {h} ^ {\ alpha} f (t) =\ frac {1} {h ^ {\ alpha}} \ sum \ limits_ {j =0} ^ {t} (- 1) ^ {j } {\ alpha \ escolha j} f (tj). $$ (4)
Existem vários esquemas de discretização para o GL Eq. (4). Os mais populares incluem diferenças anteriores (Euler), trapezoidais (Tustin) e operadores Al Alaoui. Usando o método de Euler, a derivada fracionária em momentos de tempo discretos k pode ser apresentado como
$$ \ Delta_ {h} ^ {\ alpha} f (k) =\ frac {1} {h ^ {\ alpha}} \ sum \ limits_ {j =0} ^ {k} (- 1) ^ {j } {\ alpha \ escolha j} f (kj), \; k =0,1, \ ldots. $$ (5)
A soma infinita das amostras anteriores deve ser em sistemas reais limitada a um valor finito devido à memória limitada e tempo de cálculo limitado. Agora, a aproximação de tempo discreto truncado ou de comprimento finito de GL é
$$ \ Delta ^ {\ alpha} f (k) =\ frac {1} {h ^ {\ alpha}} \ sum \ limits_ {j =0} ^ {L} (- 1) ^ {j} {\ alfa \ escolha j} f (kj), \; k =0,1, \ ldots, $$ (6)
onde f ( l ) =0 para l <0 e L é o comprimento do modelo (6) [23]. Reduzir o número de amostras resulta em menor precisão de cálculo. Isso é importante para sistemas operando em um tempo contínuo. Alguns outros tipos de solução são algoritmos que aproximam differo – integrais fracionários com modelos de ordem inteira. Um exemplo podem ser filtros recursivos Oustaloup [35]. Outro modelo de comprimento finito eficaz é o FFLD, sendo uma combinação do modelo truncado (6) e uma diferença baseada em Laguarre [24, 36, 37].

Todos os resultados de identificação, bem como medições de energia, são obtidos com base em todas as amostras na janela de observação (longa) L , ou seja, com precisão máxima. A Figura 1 apresenta as respostas ao degrau de integração e diferenciação obtidas com base em (6), para k =0,1,…, L e para vários valores de integração / ordem de diferenciação α . Assumindo diferentes valores de ordem α , pode-se modelar com mais precisão diferentes processos físicos, especialmente os de difusão.

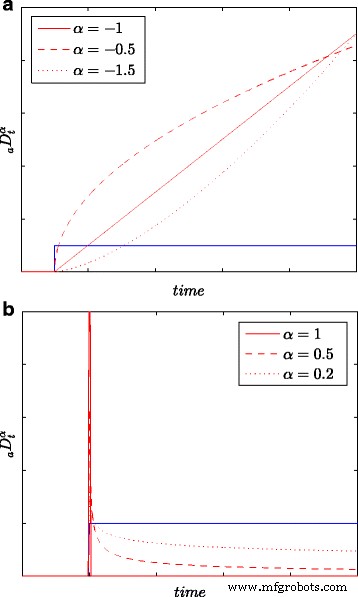
Respostas da etapa para integração ( a ) e diferenciando ( b ) modelos com vários pedidos α

Estimativa de parâmetro para modelo fracional

Os resultados de todas as medições de energia e procedimentos de identificação apresentados neste artigo foram obtidos para um supercapacitor carregado de uma fonte de tensão controlada. Em tal sistema, o supercapacitor atual i _C ( t ) deve ser limitado por um resistor R conectado em série com o supercapacitor C (Figura 2). A estimativa de todos os parâmetros do supercapacitor é realizada com base na resposta do quadripolo u _C ( t ) para a etapa de tensão u ( t ) em sua entrada. Escolhendo o valor apropriado da ordem derivada α permite levar em conta um modelo de supercapacitor dos fenômenos físicos relacionados aos processos de difusão associados à redistribuição de carga durante os processos de carga e descarga. O resistor paralelo r _P além disso, permite a modelagem da corrente de fuga. Usando o cálculo diferencial fracionário para modelar supercapacitores, a estrutura do modelo pode ser de baixa complexidade. Para supercapacitor carregado da fonte de tensão, um modelo consiste em apenas dois elementos, ou seja, um simples RC quadripolo (Fig. 2a). Para capacidades baixas, a resistência em série r _S é importante (Fig. 2b), enquanto a corrente de fuga I _L pode ser adicionalmente representado pela resistência paralela r _P (Fig. 2c). Usando o cálculo de ordem fracionária para modelar o supercapacitor, a relação entre a tensão nos terminais do capacitor e sua corrente pode ser expressa da seguinte forma
$$ i_ {C} (t) =C _ {\ alpha} \ frac {\ mathrm {d} ^ {\ alpha} u_ {C} (t)} {\ mathrm {d} t ^ {\ alpha}}, $$ (7)

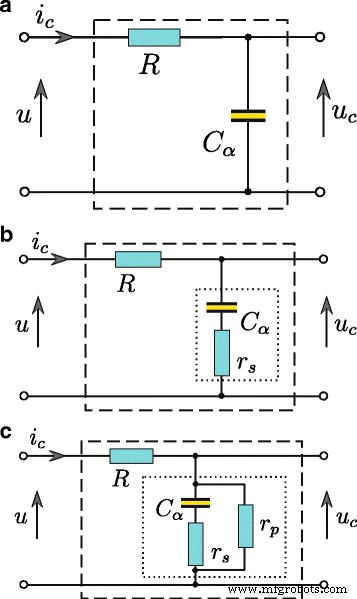
Supercapacitor RC modelos, modelo básico ( a ), expandido com uma resistência em série ( b ), e com resistência paralela adicional ( c )

onde o operador d ^α / d t ^α significa um operador de diferenciação de ordem α e a unidade SI de C _α é [F / s ^{1− α} ] A configuração básica do supercapacitor apresentada na Fig. 2a pode ser tratada como um sistema inercial de primeira ordem e pode ser representada pela função de transferência fracionária
$$ G (s ^ {\ alpha}) =\ frac {U_ {C} (s)} {U (s)} =\ frac {1} {Ts ^ {\ alpha} +1}, $$ (8 )
onde T = R C _α . Levando em consideração a resistência em série r _S (Fig. 2b), o circuito é tratado como um sistema de correção de retardo de fase com a função de transferência (compare [24])
$$ G (s ^ {\ alpha}) =\ frac {1} {T_ {1} s ^ {\ alpha} +1} + \ frac {T_ {2} s ^ {\ alpha}} {T_ {1 } s ^ {\ alpha} +1}, $$ (9)
onde T ₁ = C _α ( R + r _S ) e T ₂ = r _S C _α . Além disso, permitindo o resistor paralelo r _P representando a corrente de fuga I _L (Fig. 2c), a função de transferência do sistema pode ser expressa como
$$ G (s ^ {\ alpha}) =\ frac {T_ {2} s ^ {\ alpha} +1} {T_ {1} s ^ {\ alpha} + K}, $$ (10)
onde K = R / r _P +1, T ₁ = C ( R r _s / r _P + R + r _S ) e T ₂ = r _S C . No domínio do tempo, a Eq. (10) pode ser apresentado como
$$ \ frac {\ mathrm {d} ^ {\ alpha} u_ {C} (t)} {\ mathrm {d} t ^ {\ alpha}} =\ frac {1} {T_ {1}} (u (t) -Ku_ {C} (t)) + \ frac {T_ {2}} {T_ {1}} \ frac {\ mathrm {d} ^ {\ alpha} u (t)} {\ mathrm {d } t ^ {\ alpha}}. $$ (11)
O tempo de resposta do modelo definido por (11) foi obtido transformando-o na forma apresentada graficamente na Fig. 3, onde as operações de integração e diferenciação são de ordem fracionária α . Este modelo foi usado durante o processo de estimativa dos parâmetros do supercapacitor. O supercapacitor testado foi identificado usando o sistema apresentado na Fig. 4a. O procedimento de controle de todo o sistema foi desenvolvido utilizando o software Matlab / Simulink com xPC Toolbox. O sistema consistia em um PC desktop (xPC Target) com a placa de medição NI-DAQ instalada e um computador mestre (xPC Host). Os computadores foram interligados pela rede Ethernet. O supercapacitor foi carregado e descarregado por fonte de tensão (controlada por tensão) (Fig. 4b) de eficiência de corrente de até ± 3 A. O sistema de medição foi operado com a frequência de amostragem de 100 Hz, enquanto todas as medições e sinais de controle analógico foram processado com resolução de 16 bits [25].

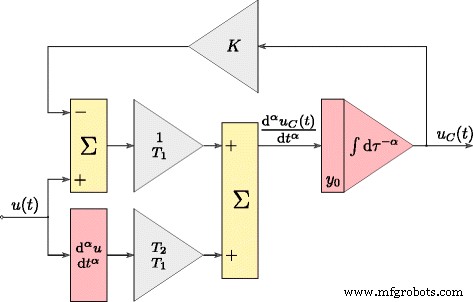
Estrutura Matlab do modelo supercapacitor no domínio do tempo

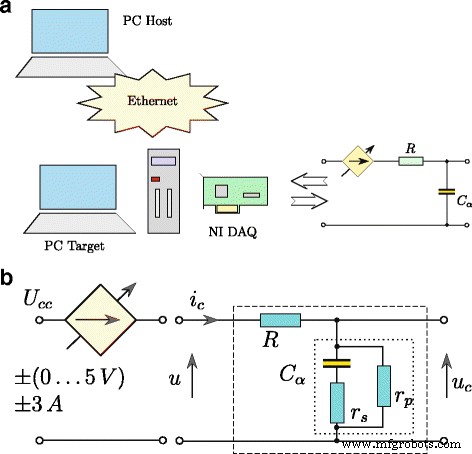
Estrutura do sistema de medição ( a ) e esquema de carregamento / descarregamento do supercapacitor ( b )

O principal método para determinar as propriedades dinâmicas de um sistema é baseado na análise da resposta ao degrau [38]. Em relação ao modelo do sistema, este método permite estimar seus parâmetros. Para este estudo, o sinal de degrau com várias tensões (0,5 / 1,0 / 1,5 / 2,0 / 2,7 V) e duração constante (500 s) foram usados (ver Fig. 5 e Tabela 2). Por outro lado, uma das aplicações típicas dos supercondensadores é o acúmulo ou entrega de energia aos sistemas de potência. Neste caso, a taxa de variação da tensão é bastante pequena. Para simular, foi utilizado o sinal de 400 mVpp e 0,03 rad / s com deslocamento de 2 V (Fig. 6). Além disso, a fim de examinar a influência das mudanças de tensão e frequência nos parâmetros estimados, vários valores destes últimos foram usados (ver Tabela 3).

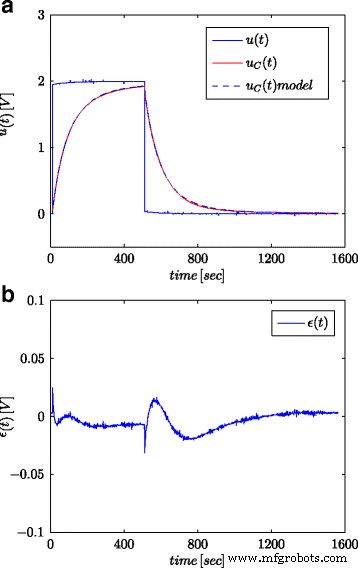
Respostas da etapa para o supercapacitor testado e seu modelo fracionário ( a ) e o erro de resposta do modelo ( b )

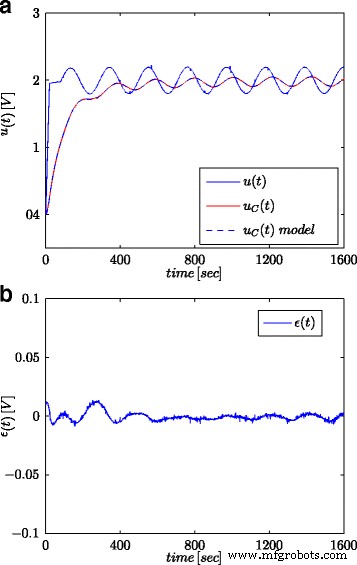
Respostas da onda sinusoidal para o supercapacitor testado e seu modelo fracionário ( a ) e o erro de resposta do modelo ( b )

Existem vários métodos para estimar os parâmetros do modelo. O principal objetivo do procedimento de identificação no domínio do tempo aplicado neste trabalho foi estimar o vetor de parâmetros desconhecidos θ =[ α , C _α , r _S , r _P ] do modelo fracionário apresentado por (11). O método dos mínimos quadrados foi usado para minimizar o erro inicial. Um critério de otimização envolveu a minimização do erro padrão \ (\ | \ epsilon (k) \ | _ {2} ^ {2} \), onde
$$ \ epsilon (k) =u_ {C} (k) - \ hat {u} _ {C} (k), $$ (12)
onde u _C ( k ) é a tensão de saída medida a partir do sistema testado no momento k , enquanto \ (\ hat {u} _ {C} (k) \) é a tensão de saída do modelo considerado para o sinal de entrada u ( k ) O problema de identificação agora se reduz a encontrar um vetor de parâmetro θ ∈ Θ _anúncio isso minimizaria o critério do quadrado J de tal maneira que
$$ \ min _ {\ theta \ in \ Theta_ {ad}} \ left \ {J =\ sum_ {0} ^ {N} {\ epsilon (k) ^ {T} \ epsilon (k)} \ right \} , $$ (13)
onde Θ _anúncio denota o conjunto de valores de parâmetros admissíveis e N significa o tempo de simulação. Existem muitos algoritmos de otimização que podem ser usados para resolver o problema (13). Os resultados apresentados neste trabalho foram obtidos através da implementação do algoritmo genético no ambiente Matlab.

Cálculo de energia

Uma mudança na energia armazenada no supercapacitor depende da energia fornecida ao capacitor por unidade de tempo e pode ser descrita como segue
$$ \ mathrm {d} E (t) =P (t) \ mathrm {d} t. $$ (14)
Expressando a potência fornecida ao capacitor como um produto da corrente e da tensão nos terminais do capacitor, a mudança na energia em determinado momento t pode ser expresso como
$$ \ mathrm {d} E (t) =u_ {C} (t) i_ {C} (t) \ mathrm {d} t. $$ (15)
A energia total durante o intervalo de tempo [ t ₁ , t ₂ ] pode ser obtido integrando as mudanças de energia ao longo desse tempo
$$ E_ {tot} =\ int_ {t_ {1}} ^ {t_ {2}} \ mathrm {d} E (t) =\ int_ {t_ {1}} ^ {t_ {2}} u_ {C } (t) i_ {C} (t) \ mathrm {d} t. $$ (16)
Contabilizando a Eq. (7), o armazenamento total de energia pode ser determinado como
$$ E_ {tot} =C _ {\ alpha} \ int_ {t_ {1}} ^ {t_ {2}} u_ {C} (t) \ frac {\ mathrm {d} ^ {\ alpha} u_ {C } (t)} {\ mathrm {d} t ^ {\ alpha}} \ mathrm {d} t. $$ (17)
Supondo que t ₁ =0 e \ (E_ {t_ {1}} =0 \), a energia total armazenada no supercapacitor durante o intervalo de tempo [0, t ] é
$$ E (t) =C _ {\ alpha} \ int_ {0} ^ {t} u_ {C} (\ tau) \ frac {\ mathrm {d} ^ {\ alpha} u_ {C} (\ tau) } {\ mathrm {d} \ tau ^ {\ alpha}} \ mathrm {d} \ tau. $$ (18)
Observe que para α =1 Eq. (18) pode ser reduzido ao clássico
$$ E (t) =\ frac {1} {2} Cu_ {C} (t) ^ {2}. $$ (19)

Resultados e discussão

Inicialmente, foi realizado o procedimento de estimação do vetor de parâmetros do modelo do supercapacitor por meio do cálculo fracionário. A estimativa foi realizada com base no sistema apresentado na Fig. 2c, gerando um degrau de tensão ou onda senoidal em sua entrada. As respostas do modelo foram calculadas com base em (11). Os resultados obtidos pelos dois procedimentos de identificação são muito semelhantes, especialmente no caso da capacitância fracionária C _α e a ordem fracionária α (ver Tabela 1). Algumas diferenças nas estimativas de resistência da série r _S pode ser resultado de sua dependência da freqüência. O sinal de degrau consiste em muitos harmônicos de alta frequência, enquanto a onda senoidal apenas um - o 0,03 rad / s. Os resultados apresentados foram obtidos para o supercapacitor comercial Samwha Green-Cap EDLC (DB), classificado como 2,7 V com capacitância nominal de 100 F e 8 m Ω resistência máxima série equivalente ( r _S ) a 1 kHz.

As Figuras 5a e 6a mostram a voltagem medida do supercapacitor e as respostas do modelo calculado, para sinais de degrau e sinusoidal, respectivamente, enquanto as Figs. 5b e 6b mostram o erro de resposta do modelo.

Todos os resultados obtidos mostram alta consistência entre as respostas do modelo e as medidas reais, apesar de modelos relativamente simples terem sido propostos. Algumas discrepâncias podem resultar do fato de que os parâmetros do modelo devem ser estimados no sistema de supercapacitor carregado e descarregado usando a fonte de corrente [25]. Além disso, estimativas muito altas de r _P pode sugerir que esta resistência poderia ser excluída do modelo de supercapacitor mostrado na Fig. 2c. Essas estimativas muito altas e suas grandes discrepâncias para diferentes entradas indicam que os sinais de teste usados para estimar este parâmetro não são adequados. O modelo (10) foi utilizado como a forma mais geral. Porém, para determinar com precisão todos os seus parâmetros, foi necessário utilizar outros procedimentos e sinais de teste. O valor de r _P caracteriza a corrente de fuga I _L e deve ser determinado usando o sinal de tensão constante, mas por um longo tempo - da ordem de várias dezenas de horas.

Embora o objetivo principal do estudo fosse medir a energia, várias condições de excitação afetaram amplamente todas as estimativas dos parâmetros (ver Tabela 2). Por exemplo, o aumento da amplitude do degrau de tensão alterou significativamente a ordem de integração fracionária, como resultado do efeito crescente dos fenômenos de difusão dentro do supercapacitor. Também pode ser visto na Tabela 2 que o supercapacitor é bastante não linear. Como resultado das mudanças na ordem de integração, a variação da capacidade fracionária também é observada. Isso também se aplica à excitação sinusoidal. Os valores dos parâmetros estimados - especialmente α e C _α —Depende da amplitude e frequência (consulte a Tabela 3). Para frequências baixas, o valor da amplitude é importante, enquanto para frequências mais altas o supercapacitor se comporta como se estivesse excitado com uma tensão constante.

Cálculo de energia

As Figuras 7a e 8a mostram os valores medidos da tensão e da corrente do supercapacitor para a configuração apresentada na Fig. 4b. Esses valores foram usados para o cálculo da energia total armazenada no capacitor (marcado como E ₁ nas Figs. 7b e 8b) de acordo com (16). Assim como para os processos de identificação dos parâmetros, os cálculos foram realizados tanto para o degrau de tensão quanto para a onda senoidal na entrada do sistema. A energia calculada dessa forma para cada tempo t foi comparada com a energia calculada com base na tensão e capacidade de acordo com (19) (marcada como E ₃ nas Figs. 7b e 8b) e energia calculada com cálculo de ordem fracionária (marcada como E ₂ nas Figs. 7b e 8b) de acordo com (18). Para a Eq. (19), um valor nominal de supercapacitor foi adotado ( C _n ), enquanto em (18) foi utilizado o valor obtido no processo de estimação apresentado na Tabela 1. A Figura 7b mostra os resultados das medições e cálculos de energia para a etapa de tensão, enquanto a Fig. 8b mostra essas mesmas quantidades para a onda senoidal. Cálculos semelhantes foram feitos para diferentes níveis de tensão e excitações senoidais. A Figura 9a, b mostra um exemplo de energias medidas e calculadas para duas etapas de tensão de 0,5 V e 2,7 V, respectivamente. A Figura 10 mostra as variações de energia para um sinal senoidal com frequência de 0,03 rad / seg e diferentes amplitudes de 0,1 / 0,25 / 0,5 e 0,7 V. Pode-se observar que as diferenças nos valores de energia determinados correspondem a diferenças nos valores estimados da ordem fracionária α . Quanto maior for a diferença do valor - 1, maior será a diferença nas energias calculadas.

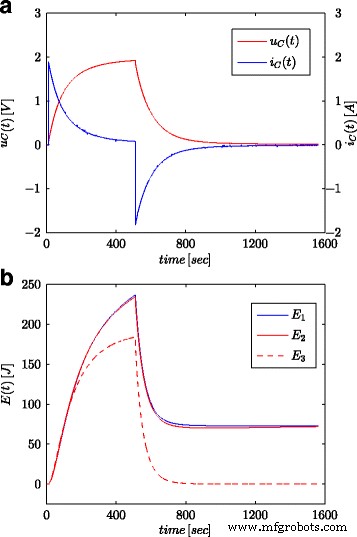
Respostas escalonadas para tensão e corrente do supercapacitor ( a ) e valores de energia calculados ( b )

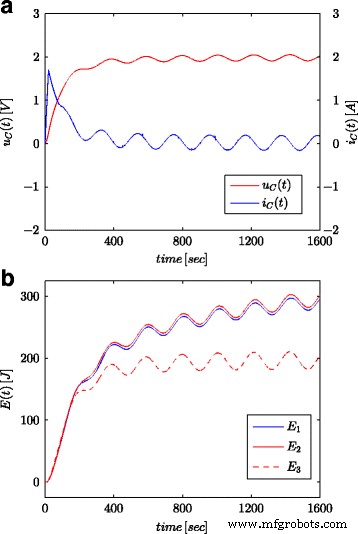
Respostas sinusoidais para tensão e corrente do supercapacitor ( a ) e valores de energia calculados ( b )

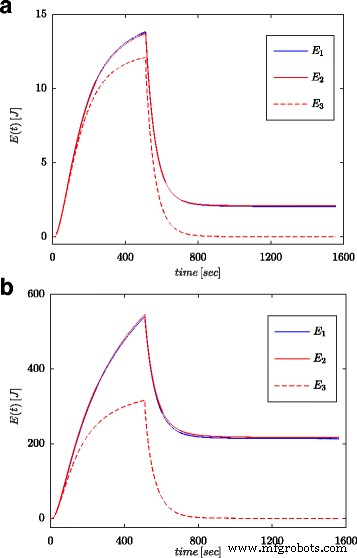
Quantidades de energia calculadas para excitações de passo de 0,5 V ( a ) e 2,7 V ( b )

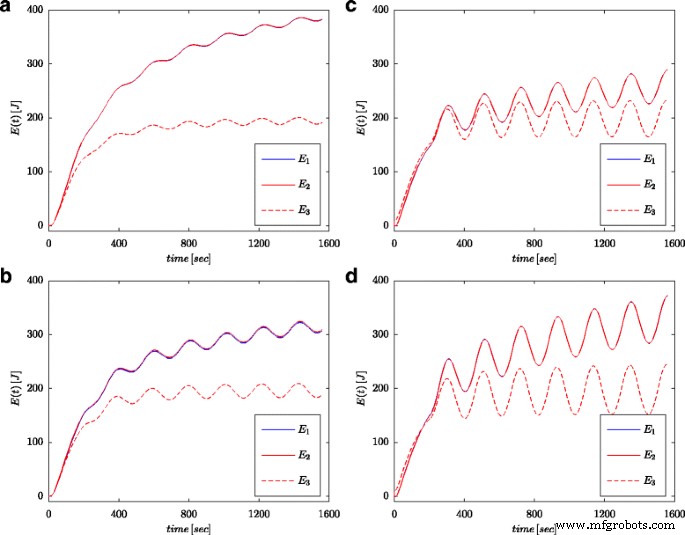
Quantidades de energia calculadas para excitações senoidais com frequência 0,03 rad / se amplitudes 0,1 V ( a ), 0,25 V ( b ), 0,5 V ( c ), e 0,7 V ( d )

Discussão

O uso de eletrodos de material poroso em supercondensadores em forma de carvão ativo isolado por um separador muito fino e o uso de mecanismos de acumulação de carga como a chamada camada dupla, proporciona um enorme aumento em sua capacidade. No entanto, a aplicação de novos materiais e novas soluções de design resulta no fato de que os cálculos matemáticos tradicionais na forma de derivadas de ordem inteira e integrais parecem imprecisos. As medições e cálculos realizados comprovam a natureza de ordem fracionária dos supercondensadores. Por estimativa correta de ordem não inteira α de derivada / integral, pode-se modelar com precisão fenômenos e processos que ocorrem dentro do supercapacitor usando modelos matemáticos simples.

Levando em consideração o valor real da energia acumulada determinado por (16), o modelo de ordem inteira com parâmetros nominais (19) subestima a quantidade de energia, enquanto o modelo fracionário (18) indica quase o mesmo valor.

Os testes e medições realizados foram relacionados ao carregamento e descarregamento do supercapacitor por uma fonte de tensão. Em condições industriais, os supercapacitores são geralmente carregados e descarregados por fontes de corrente. Isso pode mudar a natureza do sistema porque o capacitor não é mais um sistema inercial, mas se torna um típico integrador. No entanto, as medições realizadas pelo autor também indicam a ocorrência de processos de difusão nesses casos. De qualquer forma, a utilidade da derivada / integral de Gründwald-Letnikov é confirmada aqui. Outra questão está relacionada com a implementação do operador diferencial integral GL como, por exemplo, a diferença GL finita ou truncada (6), que pode ser computacionalmente onerosa. Em pesquisas futuras, compararemos os aproximadores de Oustaloup [35] e FFLD [24, 36, 37] para resolver efetivamente o problema de implementação.

A quantidade de armazenamento de energia no supercapacitor calculado apenas no valor medido da tensão terminal do supercapacitor e usando o modelo (19) não é apropriado. O modelo (19) só é válido se a corrente do capacitor for caracterizada pela derivada de ordem inteira da tensão do capacitor ( i _C ( t ) =d u _C ( t ) / d t ) Isso não é verdade para o supercapacitor, devido à sua construção e aos materiais especiais usados. No entanto, o mesmo problema ocorre com supercapacitores muito grandes carregados pela fonte de corrente. Existem também elementos bastante novos como super-baterias. Em todas essas aplicações, as mudanças de corrente não são caracterizadas pela derivada de ordem inteira da tensão do terminal como consequência das propriedades específicas desses elementos.

Conclusões

Neste artigo, uma nova abordagem para estimar a quantidade de energia acumulada em supercondensadores foi apresentada. A análise foi conduzida aproveitando certas propriedades exclusivas dos modelos de ordem fracionária. Foi demonstrado que a aplicação de tal modelagem sofisticada leva a resultados muito precisos, que podem ser obtidos mesmo que os modelos em si não sejam de alta complexidade. Isso se deve a uma habilidade natural da dinâmica de ordem não-inteira para modelar processos de difusão, assim como a redistribuição de carga em supercapacitores. Os resultados deste trabalho confirmaram a natureza fracionária dos supercondensadores.

Influência da rigidez elástica e adesão da superfície no salto de nanopartículas Avaliação de estruturas de grafeno / WO3 e grafeno / CeO x como eletrodos para aplicações de supercapacitor

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias