Geração de terceiro harmônico plasmônico de alta eficiência com grafeno em uma grade difrativa de silício na região do infravermelho médio

Resumo

Beneficiando-se da grande suscetibilidade não linear de terceira ordem do grafeno e da intensidade de campo significativamente aumentada dos plasmons de grafeno (GPs), o grafeno tem mostrado grande potencial para aumentar a eficiência de conversão da geração de terceiro harmônico plasmônico. No entanto, ainda falta uma configuração eficaz que possa excitar os GPs de frequência fundamental (FF) e guiar os GPs de frequência de terceiro harmônico (THF) gerados simultaneamente. Aqui, propusemos uma grade de silício difrativa sob uma folha de grafeno para gerar e transmitir THF GPs. Os GPs FF são eficientemente excitados iluminando uma onda plana de incidência normal devido à ressonância de modo guiado e, em seguida, são convertidos em GPs THF com uma grande eficiência de conversão, originada da intensidade de campo gigante dos GPs FF. Demonstramos numericamente que, uma grande eficiência de conversão de geração de terceiro harmônico de 3,68 × 10 ⁻⁷ pode ser realizado com uma pequena densidade de potência incidente de 0,19 MW / cm ² em 28,62 μm. Além disso, os THF GPs gerados podem ser guiados de forma eficiente ao longo de guias de ondas de GP de baixa perda que são conectados a ambos os lados da seção de grade. Nossos resultados podem estimular a produção de fontes de luz à base de grafeno para fotônica de silício no infravermelho médio e distante.

Introdução

A geração de harmônicos é um processo óptico não linear, no qual N fótons com a mesma frequência ω interagindo com um material não linear são combinados para gerar novos fótons com frequência Nω . Como um meio de estender fontes de luz coerentes a comprimentos de onda curtos, a geração de terceiro harmônico (THG) atraiu um tremendo interesse de pesquisa. Convencionalmente, a geração de harmônicos de alta eficiência é realizada em cristais exóticos, mas que compromete a integração fotônica de alta densidade [1]. O silício se tornou a escolha de material maduro como um transportador óptico de informações para transmitir sinais de luz em circuitos fotônicos altamente integrados. Efeitos ópticos não lineares, como espalhamento Raman estimulado [2] e THG [3,4,5], têm grande potencial para ampliar as funcionalidades da fotônica de silício. No entanto, a emissão de luz eficiente com o uso de silício permanece um problema desafiador devido ao seu gap indireto. Usar interações ópticas não lineares, como THG, parece uma abordagem bastante promissora para fornecer luz coerente para fotônica de silício. Em geral, a eficiência de conversão de THG (CE) para um guia de onda óptico pode ser aprimorada usando a combinação de fase entre o modo fundamental e o modo de terceiro harmônico. Este método normalmente requer configurações complicadas, que geralmente são difíceis de implementar em situações práticas. Um método eficaz e robusto para melhorar o THG CE pode ser feito aumentando a intensidade da luz dentro do material não linear, o que nos oferece a oportunidade de relaxar as exigências rigorosas para a condição de combinação de fases. Isso foi realizado recentemente usando cristais fotônicos de silício de luz lenta com fator de qualidade ultra-alta [3,4,5], microbastões de sílica de pequeno volume modal [6] e plasmons de superfície [7,8,9,10]. Foi relatado que os cristais fotônicos de silício melhoraram o THG CE para a magnitude de ~ 10 ⁻⁷ devido à velocidade de grupo reduzida de c / 40 [4]. Muito recentemente, os plasmons de superfície provaram ser capazes de aumentar o THG CE para a ordem de 10 ⁻⁵ devido ao forte aumento do campo elétrico [7].

Nos últimos anos, o comprimento de onda de operação da fotônica de silício se estendeu para as regiões do infravermelho médio e distante (IV) devido a muitas aplicações potenciais, como sensoriamento químico e biológico [11]. O uso de plasmônicos em regiões de infravermelho médio e distante é atraente porque a perda de propagação de um guia de onda plasmônica diminui drasticamente em comprimentos de onda mais longos e também porque a seção transversal de modo de tais guias de onda é sub-comprimento de onda, o que aumentaria significativamente as interações luz-matéria, como Conversão de THG [7,8,9,10, 12, 13]. Estudos recentes provaram que o grafeno serve como um excelente material óptico não linear para aumentar o efeito não linear, levando a várias aplicações, incluindo mistura de quatro ondas [14, 15], THG [16,17,18], comutação totalmente óptica [19], e biestabilidade ótica [20, 21], devido à sua grande susceptibilidade ótica não linear de terceira ordem. Especialmente, o limiar observado de biestabilidade ótica pode ser bastante reduzido, graças à grande suscetibilidade ótica não linear de terceira ordem do grafeno [20, 21]. Mais interessante, em contraste com o modo plasmon em metais, plasmons de grafeno (GPs) têm vetores de onda significativamente maiores, bem como confinamento de luz muito maior, o que indica a capacidade de aumentar ainda mais o CE de THG [13]. No entanto, um acoplamento direto entre os GPs de frequência fundamental (FF) e as ondas de radiação é evitado devido ao seu descasamento de momento, o que torna a implementação desse esquema uma questão difícil na prática. É por esta razão que os pesquisadores empregaram a ressonância de modo guiado de grades para resolver o problema de acoplamento [12, 18, 20]. O esquema proposto na Ref. [18] é propositalmente projetado para excitar diretamente os GPs FF e, portanto, aumentar o CE de ondas de espaço livre de frequência de terceiro harmônico (THF) no domínio terahertz.

Neste artigo, também usamos a ressonância de modo guiado de grades para excitar com eficiência os FF GPs nas folhas de grafeno. Diferente da configuração na Ref. [18] onde os GPs são usados ​​para aumentar o CE de ondas de espaço livre THF no domínio terahertz, aqui, os GPs são utilizados para gerar THF GPs em frequências infravermelhas em um chip de silício. A intensidade de campo gigante de FF GPs em combinação com grande susceptibilidade não linear de terceira ordem do grafeno resulta em um CE visivelmente melhorado de THF GPs na folha de grafeno em regiões de infravermelho médio e distante. Notamos um estudo anterior sobre o uso de condição de correspondência de quase-fase para melhorar o CE de THF GPs em uma superfície de grafeno [13]. No entanto, enfatizamos aqui, embora um alto CE entre FF e THF GP seja alcançável na Ref. [13], um acoplamento direto entre as ondas radiativas e os GPs está faltando. Em contrapartida, o esquema apresentado não só pode ser acoplado diretamente com as ondas FF espaciais, mas também pode gerar de forma altamente eficiente os THF GPs, tornando a proposta adequada para integração em uma plataforma fotônica de silício. Além disso, os conversores de frequência plasmônica demonstrados têm as vantagens de compactação e alta CE, enquanto requerem uma pequena potência incidente [22, 23].

Métodos

A condutividade da superfície do grafeno pode ser estimada pela fórmula de Kubo amplamente usada sob a suposição de potencial químico (também denominado como energia de Fermi), μ _c . Nas frequências infravermelho e terahertz, com | μ _c | ≫ k _B T ( k _B é constante de Boltzmann e T é a temperatura), a condutividade da superfície do grafeno pode ser aproximada como
$$ {\ displaystyle \ begin {array} {l} {\ sigma} _g =i \ frac {e ^ 2 {k} _BT} {\ pi {\ mathrm {\ hslash}} ^ 2 \ left (\ omega + i {\ tau} ^ {- 1} \ right)} \ left [\ frac {\ mu_c} {k_BT} +2 \ ln \ left (\ exp \ left (- \ frac {\ mu_c} {k_BT} \ right ) +1 \ direita) \ direita] \\ {} \ kern2.25em + i \ frac {e ^ 2} {4 \ pi \ mathrm {\ hslash}} \ ln \ left [\ frac {2 \ left | { \ mu} _c \ right | - \ mathrm {\ hslash} \ left (\ omega + i {\ tau} ^ {- 1} \ right)} {2 \ left | {\ mu} _c \ right | + \ mathrm {\ hslash} \ left (\ omega + i {\ tau} ^ {- 1} \ right)} \ right] \ end {array}} $$ (1)
onde e é a carga do elétron, ℏ é a constante de Planck reduzida, ω é a frequência radiana, e τ é o tempo de relaxamento do momentum que representa o mecanismo de perda. Em nosso estudo, a temperatura de trabalho é considerada T =300 K. Tomando a folha de grafeno individual como uma monocamada não interagente, a condutividade óptica do grafeno de poucas camadas é nσ _g [24], onde n é o número de camadas de grafeno ( n <6). Modelamos o grafeno como um material anisotrópico e a permissividade efetiva no plano pode ser escrita como [25, 26].
$$ {\ varepsilon} _x ={\ varepsilon} _z =1 + \ frac {in {\ sigma} _g {\ eta} _0} {k_0 {d} _g} $$ (2)
onde η ₀ (=377 Ω) é a impedância do ar, k ₀ é o vetor de onda no ar, e d _g é a espessura total de n - folhas de grafeno de camada. A permissividade fora do plano do grafeno, ε _y , é mantido constante em 2,5, independentemente do nível de Fermi [27, 28].

Resultados e discussão

Excitação de GPs FF com uma grade de silicone

Em primeiro lugar, consideramos a excitação dos FF GPs e a geração dos THF GPs em folhas de grafeno sustentadas por grade dielétrica (GSSDG) como mostrado na Fig. 1. Considerando a situação prática de que a área do grafeno pode ser centenas de vezes maior do que a seção da grade, presume-se que as folhas de grafeno são planas no topo das grades e não se conformam com as grades. Observamos alguns estudos de pesquisa em GP apoiados por folhas de grafeno sustentadas por grades onde as folhas de grafeno são assumidas como planas [12, 13]. Especialmente, descobrimos que os resultados experimentais são bem consistentes com os resultados da simulação, onde as folhas de grafeno são consideradas planas na modelagem [12]. O GSSDG é considerado infinito ao longo de x direção e periódica ao longo de z direção. A espessura da camada de grade de silício sob as folhas de grafeno é considerada como sendo 2 μm. Neste caso, a camada de grade pode ser considerada infinitamente espessa na modelagem, uma vez que o substrato de silício abaixo da grade não afeta a distribuição de campo dos GPs no modelo de grade de grafeno. A relação dispersiva dos GPs apoiados por esta configuração pode ser expressa como [29].
$$ \ frac {\ varepsilon_ {r1}} {\ sqrt {\ beta ^ 2 - {\ varejpsilon} _ {r1} {k} _0 ^ 2}} + \ frac {\ varejpsilon_ {r2}} {\ sqrt { \ beta ^ 2 - {\ varepsilon} _ {r2} {k} _0 ^ 2}} =- \ frac {in {\ sigma} _g} {{\ omega \ varepsilon} _0} $$ (3)
onde β é a constante de propagação dos GPs ao longo de z- eixo, ε ₀ é a permissividade no ar, e ε _{r 1} (=1) e ε _{r 2} são as constantes dielétricas dos meios dielétricos acima e abaixo das camadas de grafeno, respectivamente. Como o período da grade é muito menor do que o comprimento de onda da luz no ar, a grade de silício pode ser modelada aproximadamente como um meio efetivo com a permissividade equivalente [30].
$$ {\ varejpsilon} _ {r2} =f {\ varejpsilon} _ {\ mathrm {silício}} + \ left (1-f \ right) {\ varejpsilon} _0 $$ (4)
onde ε _silício (=11,9) é a permissividade do silício em frequências infravermelho e terahertz [31], e f (= w / p ) é a taxa de enchimento do silício ( f é fixada em 0,5 neste trabalho).

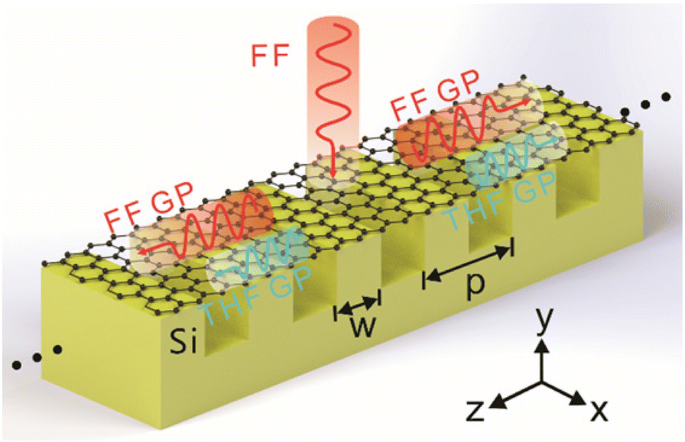
O esquema do GSSDG como um conversor de comprimento de onda THG. Os GPs FF (curvas vermelhas) são excitados com uma onda plana polarizada x de incidência normal de FF e então geram os GPs THF (curvas azuis) devido às grades de silício sob as folhas de grafeno. O período da grade é p e w denota a largura do silício

A relação de dispersão dos GPs no GSSDG para diferentes parâmetros ( τ , μ _c e d _g ) é mostrado na Fig. 2. Em todo o trabalho, o domínio de tempo de diferenças finitas bidimensionais (FDTD) com um software comercial da Lumerical FDTD Solution é conduzido para fazer a modelagem numérica. Na simulação desta parte, os limites de camada correspondentes perfeitos e os limites periódicos são usados ​​no y e z direções, respectivamente, enquanto toda a estrutura é considerada infinita ao longo do x direção. Os tamanhos de malha com 0,1 nm ao longo de y direção e 10 nm ao longo de z direção são usados ​​para descrever o grafeno, enquanto malhas não uniformes com um valor máximo de 20 nm ao longo de y direção e malha uniforme de 10 nm ao longo de z direção são adotadas nas regiões além das folhas de grafeno. Pode-se observar na Fig. 2a, d, g que, dentro da faixa de comprimento de onda considerada, o vetor de onda dos GPs é dezenas de vezes maior que o do ar, o que indica que o campo óptico dos GPs está fortemente confinado ao superfície de grafeno. No entanto, o descasamento de fase entre os GPs e as ondas de radiação impede o acoplamento direto entre eles. A grade difrativa de silício abaixo das folhas de grafeno mostradas na Fig. 1 pode fornecer um momento adicional para superar a diferença do vetor de onda de modo que os GPs FF possam ser eficientemente excitados com uma incidência de onda plana. O período de grade, p , precisa atender à equação de correspondência de fase como
$$ \ operatorname {Re} \ left ({\ beta} _ {\ mathrm {FF}} \ right) =j2 \ pi / p + {k} _0 \ sin \ theta $$ (5)
onde β _FF é a constante de propagação dos GPs FF ao longo de z -eixo, j é a ordem de difração, e θ é o ângulo de incidência. Para excitar os GPs FF de comprimento de onda efetivo de λ _FF com a ordem de difração fundamental j =1 sob a condição de incidência normal θ =0, a seguinte expressão deve ser satisfeita
$$ {\ lambda} _ {\ mathrm {FF}} =\ operatorname {Re} \ left ({n} _ {\ mathrm {eff}} \ right) p $$ (6)
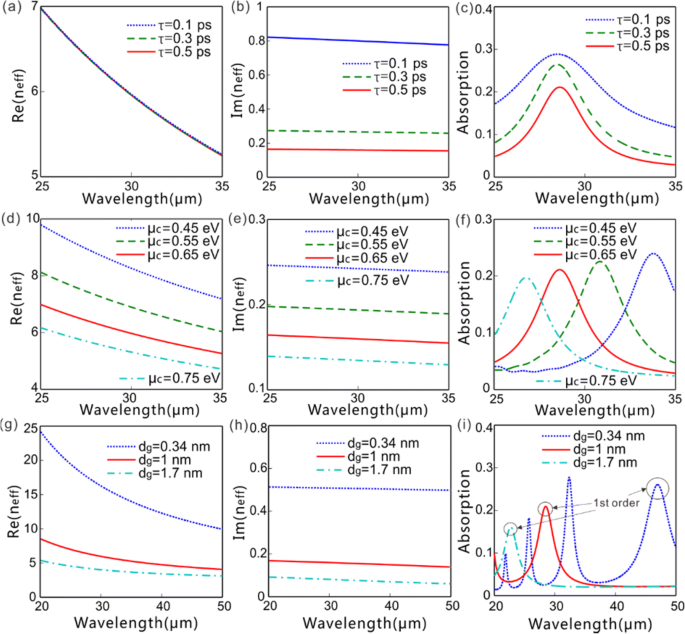
O verdadeiro [Re ( n _eff )] e imaginário [Im ( n _eff )] partes do índice efetivo e absorção versus comprimento de onda com diferentes valores de μ _c , τ e d _g . a - c Re ( n _eff ), Im ( n _eff ), e absorção versus comprimento de onda ( τ =0,1, 0,3 e 0,5 ps, associado a μ =0,14, 0,42, 0,69 m ² V ⁻¹ s ⁻¹ , respectivamente) com μ _c =0,65 eV e d _g =1 nm. d - f Re ( n _eff ), Im ( n _eff ), e absorção versus comprimento de onda ( μ _c =0,45, 0,55, 0,65 e 0,75 eV) com τ =0,5 ps e d _g =1 nm. g - i Re ( n _eff ), Im ( n _eff ), e absorção versus comprimento de onda [ d _g =0,34 nm ( n =1), 1 nm ( n =3), e 1,7 nm ( n =5)] com μ _c =0,65 eV e τ =0,5 ps. Para todos os casos, o período de grade é fixado em p =4 μm

A Figura 2 apresenta a dependência do real [Re ( n _eff )] e imaginário [Im ( n _eff )] parte dos índices efetivos e absorção no comprimento de onda da luz com diferentes valores de τ , μ _c e d _g . Aparentemente, explica como os parâmetros do grafeno influenciam os GPs FF excitados sob a iluminação de uma onda plana polarizada x de incidência normal de FF, onde o período de grade é fixado em 4 μm. Tanto o real [Re ( n _eff )] e partes imaginárias [Im ( n _eff )] dos índices de refração efetivos dos GPs FF diminui com o aumento do comprimento de onda da luz dentro da faixa de comprimento de onda considerada (Fig. 2a, b, d, e, g, h). Isso significa que, com um comprimento de onda de luz mais curto, os GPs ficam mais fortemente confinados em torno das folhas de grafeno, resultando em uma constante de propagação maior e uma perda de propagação maior. A absorção é altamente sensível ao comprimento de onda e aumenta drasticamente à medida que o comprimento de onda incidente se aproxima do comprimento de onda de ressonância (Fig. 2c, f, i). O tempo de espalhamento do portador τ determina a mobilidade da portadora μ no grafeno como \ (\ tau ={\ mu \ mu} _c / e {\ nu} _F ^ 2 \) com a velocidade de Fermi de ν _F =9,5 × 10 ⁴ em. Considerando que uma mobilidade de portadora de μ > 10 m ² V ⁻¹ s ⁻¹ foi obtido experimentalmente em grafeno suspenso de alta qualidade [32], o que leva a τ > 1,5 ps, nossa configuração de τ ≤ 0,5 ps pode refletir a perda prática de transporte do grafeno de forma conservadora. O τ , associado à mobilidade da portadora μ , influencia suavemente o Re ( n _eff ) e o comprimento de onda de excitação de FF GPs, mas afeta muito o Im ( n _eff ) e absorção (Fig. 2a-c). O μ aprimorado _c diminui Re ( n _eff ) e Im ( n _eff ) simultaneamente, portanto, reduz o comprimento de onda de ressonância de FF GPs em conformidade (Fig. 2d – f). O Re ( n _eff ), Im ( n _eff ), e o comprimento de onda de ressonância de FF GPs reduz com o aumento da espessura do grafeno, correspondendo ao número de camadas de grafeno (Fig. 2g – i).

A seguir, pegamos τ =0,5 ps, μ _c =0,65 eV e d _g =1 nm como exemplos. A relação de dispersão dos GPs no GSSDG é mostrada na Fig. 3a, onde as curvas de dispersão calculadas concordam bem com os resultados da simulação obtidos pelo software comercial Lumerical FDTD Solutions. A Figura 3b mostra a resposta óptica das folhas de grafeno com e sem a grade de silício. Pode ser visto claramente que a eficiência de absorção (mais de 20%) é significativamente aumentada em λ =28,62 μm quando a grade está envolvida ( p =4 μm). Em contraste, a eficiência de absorção é mantida em um nível baixo (abaixo de 2%) em toda a faixa espectral considerada, se a grade não for levada em consideração. A absorção visivelmente aumentada para o primeiro caso pode ser atribuída à excitação dos GPs em λ =28,62 μm. Podemos encontrar no | E | distribuições em λ =28,62 μm (Fig. 3c) que o GPs excitado é o modo de ressonância de onda guiada fundamental ( j =1). Pode-se ver na Fig. 3d que o comprimento de onda ressonante do modo fundamental com respeito ao período de grade das simulações numéricas, concorda bem com o resultado teórico previsto pela Eq. (6).

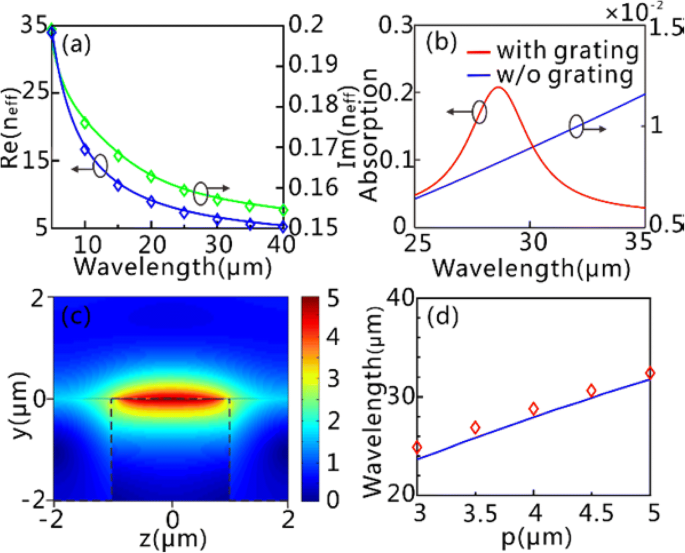
GPs FF e aprimoramento de campo no GSSDG. a Curvas de dispersão dos GPs no GSSDG. As linhas sólidas azuis e verdes correspondem ao real [Re ( n _eff )] e imaginário [Im ( n _eff )] parte do índice efetivo recuperado da Eq. (3), respectivamente, enquanto os losangos azul e verde são obtidos a partir de simulações numéricas. b Espectros de absorção com substrato de grade (linha vermelha) e substrato de silício puro sem a grade (linha azul). c O normalizado | E | distribuições do modo GPs fundamentais em 28,62 μm. As linhas tracejadas pretas delineiam a camada de silício. d O comprimento de onda de excitação do modo GPs fundamental versus o período de grade. A linha azul é recuperada da Eq. (6), e os losangos vermelhos são de simulação numérica. Em b e c , P é definido como 4 μm. Todos os resultados da simulação são recuperados pelo software comercial Lumerical FDTD Solutions

Deve-se notar que, um campo plasmônico bastante intensificado na superfície do grafeno ocorre devido à redução significativa da velocidade de grupo dos GPs FF (dezenas de vezes menor do que a velocidade da luz no ar). O campo plasmônico sofre aumento de campo elétrico 5 vezes mais alto que as ondas planas iluminantes, o que pode ser altamente esperado para gerar THF GPs com um CE significativamente melhorado, em combinação com a grande não linearidade óptica de terceira ordem do grafeno [16, 17]. A resposta não linear do grafeno pode ser descrita pelo coeficiente de condutividade não linear definido como [17].
$$ {\ sigma} _3 \ left (\ omega \ right) =i \ frac {3 {e} ^ 2 {\ left ({ev} _F ^ 2 \ right)} ^ 2} {32 \ pi {\ mathrm {\ hslash}} ^ 2 {\ mu} _c {\ omega} ^ 3} $$ (7)
onde a velocidade de Fermi ν _F =9,5 × 10 ⁴ em.

Geração de THF GPs

Em seguida, comparamos a intensidade do campo elétrico dos THF GPs na superfície do grafeno quando as folhas de grafeno são sustentadas com e sem grade. As condições de contorno nas simulações FDTD são as mesmas usadas nas Figs. 2 e 3. A intensidade do campo elétrico normalizado (NEFI) em função do comprimento de onda é apresentada na Fig. 4a, quando as folhas de grafeno são iluminadas por luz de onda contínua de incidência normal (CW) com densidade de potência de 0,11 MW / cm ² e o comprimento de onda central de 28,62 μm. Aqui, o NEFI é obtido normalizando a intensidade do campo elétrico para seu valor em 28,62 μm (FF) com a estrutura de grade. Pode-se observar que um pico aparente ocorre no THF no espectro NEFI com estrutura de grade (GSSDG), em comparação com o espectro NEFI sem grade envolvida. Definindo o CE como \ ({\ int} _0 ^ p {P} _y ^ {THF} dz / \ left ({P} ^ {FF} p \ right) \), onde \ ({P} _y ^ {THF } \) é o y componente do vetor de poynting em THF, e P ^FF é a densidade de potência da luz incidente, o CE atinge até 5,71 × 10 ⁻⁷ para o GSSDG. Pode-se inferir facilmente que, a excitação dos FF GPs contribui para o aprimoramento do CE dos THF GPs. As distribuições de campo da parte real de E _y no THF mostrado na Fig. 4b validar a geração de THF GPs na superfície do grafeno.

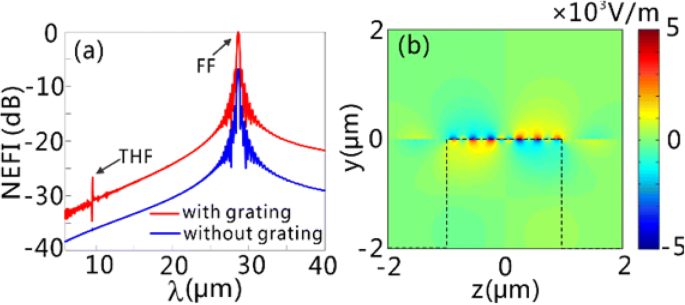
Geração de THF GPs no GSSDG. a O NEFI para a estrutura com (linha vermelha) e sem (linha azul) grade normalmente iluminada por luz CW com a densidade de potência de 0,11 MW / cm ² e o comprimento de onda central de 28,62 μm. Os dois picos na linha vermelha denotam os GPs FF ( λ =28,62 μm) e os THF GPs gerados ( λ =9,54 μm), respectivamente. b A distribuição da parte real de E _y para os THF GPs gerados. A linha tracejada preta em b representa os contornos da camada de silício. Os parâmetros estruturais do GSSDG são iguais aos da Fig. 3

O GSSDG como fonte de luz para fotônica de silício infravermelho médio

A seguir, consideramos o uso do conversor de comprimento de onda plasmônico GSSDG para fornecer diretamente a fonte de luz para os circuitos fotônicos integrados de silício. Como um exemplo mostrado na Fig. 5a, dois guias de onda de grafeno-silício plasmon (GSPWs) são fixados ao GSSDG em ambos os lados. Os GSPWs são escolhidos de forma que sejam capazes de guiar os GPs em uma ampla banda espectral cobrindo os GPs FF e THF. Uma vez que as distribuições modais de campo dos modos FF e THF GP no GSSDG (assimétrico em relação à superfície de grafeno) apresentam forte similaridade com os modos GP suportados no GSPW, pode-se então deduzir que, uma vez que a seção da grade é iluminada com incidência normal As ondas FF, os GPs FF e THF gerados acima da região da grade podem ser acoplados de forma eficiente aos GSPWs em ambos os lados. Realizamos simulações FDTD para validar nossa previsão. Os limites de camada correspondentes do prefeito são usados ​​em y e z direções na modelagem. Simulamos uma onda de luz FF de incidência normal que atinge a seção da grade e mostramos as distribuições do campo elétrico para os GPs FF e THF (Fig. 5b, c). Uma fonte de luz de campo total / campo espalhado é usada para garantir que apenas a seção da grade seja iluminada com luz incidente na simulação [33]. O limite de absorção perfeitamente combinado foi usado para absorver totalmente todas as ondas de luz que atingem o limite da região de computação. A Figura 5b mostra que os GPs FF são excitados na superfície de grafeno acima da grade e, em seguida, se propagam ao longo dos GSPWs em ambos os lados. Na Fig. 5c, podemos ainda encontrar a aparência dos THF GPs na superfície do grafeno, tanto na seção da grade quanto nos GSPWs. Aqui, o CE é definido como
$$ \ mathrm {CE} =\ int {P} _z ^ {T \ mathrm {HF}} \ mathrm {dz} / \ left ({P} ^ {\ mathrm {FF}} {N} _pp \ right) $$ (8)
onde \ ({P} _z ^ {\ mathrm {THF}} \) é o z -componente do vetor de potência em THF, \ (\ int {P} _z ^ {\ mathrm {THF}} \ mathrm {dz} \) é a densidade de potência de saída de THF GP no GSPW, P ^FF é a densidade de potência das ondas de luz FF incidentes, e N _p é o número do período de grade. Pode-se ver na Fig. 5d que, o CE de THG atinge o valor máximo de 3,68 × 10 ⁻⁷ (- 64,3 dB) no limite da grade e atenua exponencialmente ao longo da direção de propagação devido à perda de absorção ôhmica do grafeno.

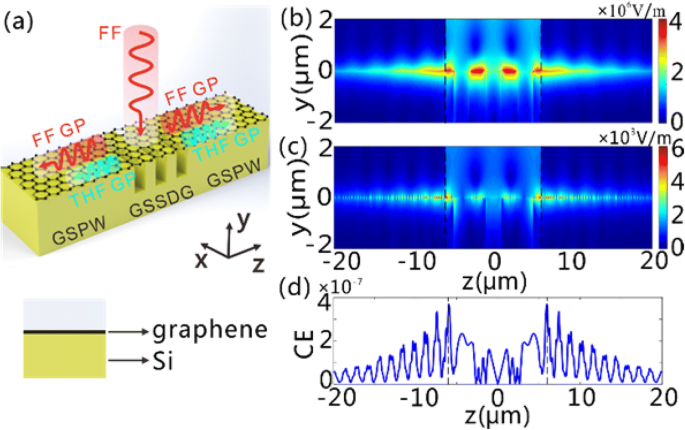
Geração de GPs FF e THF no GSSDG e nos GSPWs conectados. a Os esquemas do GSSDG e dos GSPWs conectados em ambos os lados quando uma onda plana polarizada x de incidência normal de FF ilumina a estrutura. Os THF GPs são gerados e guiados ao longo dos dois GSPWs depois que os FF GPs estão entusiasmados com o GSSDG. A seção transversal do GSPW é apresentada no painel abaixo, no qual as folhas de grafeno e a camada de Si são denotadas. b , c O | E | distribuições de b FF e c THF GPs no y - z plano conforme a seção da grade é iluminada pela luz CW com a densidade de potência de 0,19 MW / cm ² em 28,62 μm. d O CE de THG ao longo do z direção. As linhas pretas tracejadas em b - d representam as interfaces entre o GSSDG e GSPWs. Em b - d , N _p é fixado em três

É importante discutir os fatores que afetam o THG CE, que é a chave para avaliar o desempenho do dispositivo de um conversor de comprimento de onda THG. Para um processo THG, sempre se espera obter o maior CE com uma potência de bomba relativamente pequena. Estudos anteriores demonstraram que, aumentando a intensidade do campo local nos materiais não lineares de terceira ordem, obtém-se uma melhoria notável do CE de THG com uma potência da bomba significativamente reduzida [3, 4, 7]. A Figura 6a mostra a influência da densidade de potência das ondas de luz incidentes na CE máxima nos GSPWs, que é aumentada com a densidade de potência. Observe que o CE máximo atinge até 3,68 × 10 ⁻⁷ mesmo que a densidade de potência das ondas de luz incidentes seja tão baixa quanto 0,19 MW / cm ² , que é 6–7 ordens de magnitude menor do que aqueles dentro da mesma banda espectral [22, 23]. Mostramos na Fig. 6b que o número usado de período de grade, N _p , afeta o CE nos GSPWs também. Quando N _p é aumentada, uma porção de redução dos THF GPs gerados no centro da grade atinge os GSPWs por causa da perda de propagação aumentada induzida pela absorção de grafeno. No entanto, a potência de entrada, associada a N _p , apresenta aprimoramento linear. Portanto, o máximo CE dos THF GPs diminui com o aumento de N _p . Enfatizamos aqui que a densidade de potência de saída absoluta de THF GPs deve ser mais significativa para orientar o projeto de um conversor de comprimento de onda THG para aplicações práticas, uma vez que a densidade de potência incidente é fixa. Embora o máximo CE dos THF GPs esteja em N _p =2 em nosso caso, a densidade de potência de saída de THG se aproxima do máximo quando N _p ≥ 3 (Fig. 6b). Portanto, empregamos 3 períodos de grade para a demonstração da geração de THF GPs nos GSPWs. Para futura implementação experimental com o projeto atual, a área da fonte FF de entrada excede a região da grade e é mantida constante ao gerar THF GP com diferentes números de grade. Neste caso, o CE deve ser escrito como
$$ \ mathrm {CE} =\ int {P} _z ^ {\ mathrm {THF}} \ mathrm {dz} / \ left ({P} ^ {\ mathrm {FF}} S \ right) $$ (9 )
onde a área da fonte FF, S , é constante. Assim, a densidade de potência de saída será proporcional ao CE e, portanto, deve-se selecionar corretamente o número de grade ideal para maximizar a densidade de potência de saída de THF GP.

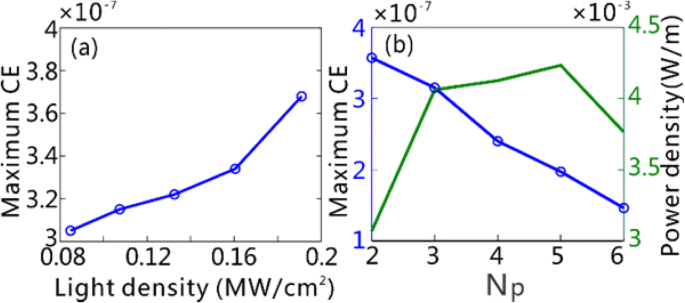
a O máximo CE de THG em função da densidade de potência incidente para N _p =3. b A CE máxima e a densidade de potência de saída máxima de THG em função do número de períodos de grade N _p usado, respectivamente. A densidade de potência incidente é fixada em 0,11 MW / cm ²

As características físicas do grafeno também podem afetar o desempenho do dispositivo de THF GPs, uma vez que a estrutura estudada mostrada na Fig. 5a está pronta. A energia Fermi, μ _c , e o número de camadas de grafeno mudará significativamente o comprimento de onda de ressonância de FF GPs (Fig. 2f, i) e, portanto, afetará o comprimento de onda de geração de THF GPs também. Em contraste, o τ , associado à mobilidade da portadora μ , mal influencia o comprimento de onda de ressonância de FF GPs, bem como o comprimento de onda de geração de THF GPs (Fig. 2c). No entanto, a perda de propagação de FF GPs e THF GPs pode ser reduzida pelo uso de um τ muito maior (Fig. 2b), o que aumenta notavelmente o CE de THF GPs. Considerando que uma mobilidade de portadora de μ > 10 m ² V ⁻¹ s ⁻¹ ( τ > 1,5 ps) é alcançável no experimento [32], nossos resultados de simulação ( τ =0,5 ps) mostrado nas (Figs. 3, 4, 5 e 6) pode apresentar de forma conservadora o desempenho do dispositivo do gerador de THF GP na Fig. 5a.

Por fim, vale a pena discutir as influências da rugosidade da superfície das folhas de grafeno no desempenho do dispositivo. A rugosidade da superfície do grafeno pode potencialmente espalhar o plasmon e, portanto, a perda de plasmon será aumentada [34]. O gerador de THF GP proposto mostrado na Fig. 5 pode ser fabricado com base na atual tecnologia de micro / nano fabricação. Pode-se primeiro girar um polimetilmetacrilato (PMMA) de 270 nm de espessura sobre o substrato de silício. A camada de PMMA é desenvolvida com MIKE \ IPA após um subsequente processo de litografia por feixe de elétrons. Depois disso, uma camada de Cr de 60 nm de espessura é depositada no resist com o método de deposição por evaporação por feixe de elétrons. O substrato de grade de silício pode ser formado com técnicas de corrosão, como máquina de plasma acoplada indutivamente. Seguido pelo método de corrosão úmida, a camada residual de Cr é removida pelo método de corrosão úmida. Por fim, as folhas de grafeno são transferidas para a grade de silício para formar a estrutura final mostrada na Fig. 5.

Conclusão

Demonstramos numericamente a geração de THF GPs em uma folha de grafeno em grades de silício com as ondas planas de incidência normal em regiões de infravermelho médio e distante. Foi demonstrado que THF GPs são gerados e transmitidos na superfície do grafeno, e o CE é dramaticamente aprimorado devido à intensidade de campo significativamente aumentada dos FF GPs excitados em combinação da grande susceptibilidade não linear de terceira ordem do grafeno. Os THF GPs gerados podem ser convenientemente acoplados a um GSPW, o que facilita muito a integração do conversor de comprimento de onda à base de grafeno em uma plataforma de silício. Our proposal can stimulate making graphene-based light sources for mid- and far-infrared photonics on a silicon platform and hence broaden the functionalities of silicon photonics, such as signal processing, spectroscopy, and sensing.

Abreviações

CE:

Conversion efficiency

CW:

Continuous wave

FDTD:

Domínio do tempo de diferença finita

FF:

Fundamental frequency

GP:

Graphene plasmon

GSPW:

Graphene-silicon plasmon waveguide

GSSDG:

Graphene sheets sustained by dielectric grating

PMMA:

Metacrilato de polimetila

THF:

Third-harmonic frequency

THG:

Third-harmonic generation

Insight sobre a captação celular e o tráfico intracelular de nanopartículas Estudo comparativo sobre a estabilidade microestrutural de níquel nanocristalino eletrodepositado pré-recozido durante a laminação da embalagem