Efeito óptico não linear aprimorado em células híbridas de cristal líquido com base em cristal fotônico

Resumo

A resposta ótica não linear de células híbridas fotorrefrativas de cristal líquido (LC) foi estudada por meio da técnica holográfica dinâmica em um arranjo de mistura de duas ondas. As células LC incluem substratos de silício não uniformes compreendendo um cristal fotônico de alcance micrométrico. Uma fina camada LC é definida entre o substrato de silício e um substrato de vidro plano coberto por um eletrodo transparente (ITO). Uma rede de difração dinâmica foi induzida no volume LC pela mistura de duas ondas de feixes de laser com aplicação simultânea de campo elétrico DC à célula. O modelo teórico da autodifração Raman-Nath foi desenvolvido. Este modelo permite o cálculo de características ópticas não lineares em amostras finas com base em dados experimentais de mistura de duas ondas e levando em consideração as perdas de luz na absorção e / ou espalhamento. As células híbridas LC demonstram forte efeito óptico não linear, prospectivo para muitas aplicações em microsistemas eletro-ópticos, como SLMs, bem como em sistemas multicanais.

Histórico

Entre as principais vantagens dos sistemas de processamento óptico está a capacidade de utilizar a alta largura de banda temporal e espacial da fotônica. Um componente fundamental nesses sistemas é um dispositivo que modula a luz. Os moduladores de luz espacial (SLM), impondo informações sobre campos de dados ópticos em sistemas de processamento óptico de informações, por muito tempo foram considerados essenciais para a exploração eficiente das capacidades de velocidade, processamento paralelo e interconexão inerentes à óptica. Esses dispositivos geralmente modificam a fase, polarização, amplitude e / ou intensidade de uma distribuição de luz espacial como uma função de informações de acionamento elétrico ou a intensidade de outra distribuição de luz [1]. As vantagens dos materiais eletro-ópticos de cristal líquido para SLMs incluem sua alta birrefringência e operação de baixa tensão. Colocar cristais líquidos em cima de circuitos integrados de silício foi proposto no início de 1980 para produzir monitores portáteis [2]. Devido à mais ampla fabricação de circuitos integrados de silício, que podem conter fotodetectores, amplificadores e elementos de memória, os SLMs de cristal líquido eletro-óptico em silício (LCoS) tornaram-se uma ferramenta padrão na maioria dos laboratórios ópticos. A próxima etapa, altamente desejada, sugere o manuseio de informações totalmente ópticas, que poderia ser alcançado por meio da modificação controlada por luz das propriedades ópticas do meio. Muitos dos SLMs opticamente endereçados adotaram a estrutura de sanduíche básica com o fotocondutor transferindo uma tensão de polarização aplicada ao sanduíche para um material de modulação, por exemplo, cristais líquidos na válvula de luz de cristal líquido (LCLV) [3].

Quase todos os efeitos ópticos não lineares existentes foram observados em composições de LC dopadas com corante, nas quais as moléculas de corante absorvedor acionam a reorientação do diretor de LC [4]. Alternativamente, a ação da luz nas moléculas fotossensíveis afeta o parâmetro de ordem do LC que, por sua vez, resulta em mudanças substanciais e rápidas dos índices de refração locais do LC [5]. No ano passado, os centros fotossensíveis populares tornaram-se nanopartículas embutidas no volume LC [6]. Os sistemas LC não absorventes também têm atraído muito interesse como válvulas de luz LC puro-nemático fotorrefrativo. O principal mecanismo óptico não linear em LC é a reorientação coletiva de moléculas em um volume de LC sob excitação a laser que frequentemente aparece com campo elétrico aplicado. No presente trabalho, usamos LC nemático puro. O mecanismo óptico não linear em células LC sugere um efeito fotorrefrativo induzido pela superfície, que altera a orientação das moléculas LC na massa iniciada a partir da superfície. Este efeito foi investigado em células LC contendo diferentes materiais de superfície, como camadas de polímero fotorrefrativo [7, 8], camadas condutoras com impurezas embutidas [9], placas de metal nobre [10] e cristais fotorrefrativos [11]. Via de regra, a orientação inicial das moléculas em uma superfície era plana. Outro tipo de células, que apresentam efeito fotorrefrativo induzido pela superfície, consistem em substratos de vidro simples cobertos com eletrodos ITO e preenchidos com um LC nemático puro, mas a principal característica estudada é a orientação homeotrópica das moléculas [12, 13]. Tal efeito é estudado no presente trabalho. Usamos, no entanto, células híbridas onde um dos substratos é um cristal fotônico feito de silício. O aprimoramento das propriedades físicas dos materiais depositados em superfícies nano ou microestruturadas, incluindo propriedades ópticas, elétricas e outras, torna-se uma das direções prioritárias da nanociência fundamental. Em nossa pesquisa, investigamos a possibilidade de fortalecimento do efeito óptico não linear em uma célula LC devido à influência de uma superfície microestruturada de um substrato, que forma a célula.

Para investigar as propriedades ópticas não lineares em células híbridas LC contendo uma superfície reflexiva, aplicamos a técnica holográfica dinâmica baseada na mistura de duas ondas de feixes de laser na geometria de reflexão [14]. Sabe-se que a holografia dinâmica é baseada em três efeitos principais, que atuam simultaneamente:(1) criação de um padrão de interferência periódica dentro de um meio não linear com o auxílio de dois ou mais feixes de laser coerentes; (2) modulação do índice de refração sob a ação desse padrão de interferência; em nosso caso, significa induzir uma grade dinâmica de fase dentro de um meio não linear; (3) autodifração dos feixes de gravação na grade dinâmica. Até agora, a mistura de ondas é conhecida como uma técnica eficaz para muitas aplicações em óptica não linear (ver, por exemplo, [15]). Basta citar a multiplexação espacial e comutação de feixes de laser, controle totalmente ótico dos parâmetros dos feixes, memória ótica dinâmica, lógica, etc. No presente trabalho, demonstramos que este método também pode ser aplicado como uma técnica experimental simples para determinar características ópticas não lineares de filmes finos. Desenvolvemos uma abordagem matemática para calcular o coeficiente de refração não linear em um meio do tipo Kerr, a partir do qual a susceptibilidade óptica não linear pode ser determinada. O modelo matemático cobre a autodifração de ondas no regime Raman-Nath, ou seja, para a condição de uma grade fina. Esta abordagem geralmente é satisfeita para a maioria das amostras finas que normalmente têm espessura de até dezenas de micrômetros. Esses meios incluem também células LC. Observe que um método alternativo para determinar a suscetibilidade não linear óptica de materiais transparentes é a técnica de varredura z [16]. Mas mostramos que o método de mistura de duas ondas é bastante simples para a realização experimental e é muito adequado para a investigação dos meios dinâmicos, incluindo aquele que funciona apenas na geometria de reflexão.

Métodos

Materiais e Amostras

A estrutura das células híbridas LC é mostrada na Fig. 1. A célula híbrida tem um tipo sanduíche, é formada por substratos de vidro e silício e preenchida com nemático LC; suas bordas são coladas. A espessura da camada LC nemática é de 20 μm. O substrato de vidro plano é coberto com eletrodo ITO. O segundo substrato é cortado de um wafer de silício dopado com fósforo, suas dimensões são 17 × 17 mm ² . Sua resistividade é 4,5 Ω⋅cm, sua espessura é 380 μm e sua orientação é 〈100〉. O substrato de silício contém duas áreas, a saber, uma superfície com parte microestruturada periódica, que na verdade é um cristal fotônico na faixa do micrômetro, e uma parte plana da superfície.

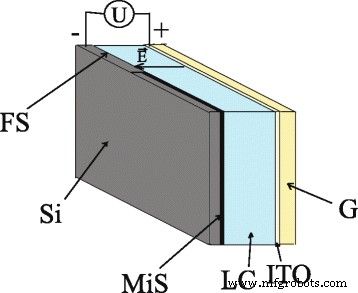
Estrutura de uma célula híbrida LC:substrato de silício ( Si ); superfície de silício microestruturada ( MiS ); superfície plana de silício ( FS ); cristais líquidos ( LC ); substrato de vidro ( G ); Eletrodo ITO ( ITO ); tensão aplicada ( U ); vetor de campo elétrico (\ (\ overrightarrow {E} \))

Os três substratos de Si, usados em nossa investigação, são mostrados na Fig. 2. As microestruturas representam poços gravados dispostos em uma matriz quadrada (os substratos 1 e 2) ou em uma matriz triangular (o substrato 3). As covas são micropiramides quadradas, que diferem pela forma, tamanho e disposição. Existem (1) pirâmides regulares, (2) pirâmides truncadas (poços) e (3) pirâmides ligeiramente truncadas. As micropiramidas regulares têm 2 μm de altura, o mesmo lado da base de 2 μm e periodicidade de 3 μm. Os poços têm parâmetros semelhantes, mas são compactados. As pirâmides ligeiramente truncadas têm o lado da base 1,5 μm e a periodicidade 3,5 μm. As microestruturas foram formadas no lado polido do wafer de silício por técnica fotolitográfica padrão seguida por ataque anisotrópico para os substratos 1 e 3, ou por ataque de plasma para o substrato 2.

Imagens de superfícies de silício microestruturadas feitas em microscópio óptico. As micropiramidas têm as seguintes formas:pirâmides regulares (1), covas (2) e pirâmides ligeiramente truncadas (3)

Dois LC nemáticos foram usados:nemático puro 5CB (4 × - ( n -pentil) -4-cianobifenil) e mistura nemática E7. Em todos os casos, a orientação molecular em uma camada de cristal líquido é homeotrópica e aparece espontaneamente em superfícies de ITO e silício com a temperatura de processamento sendo mantida não superior a 50 ° C. Investigamos quatro amostras, que diferem pela forma da microestrutura e pelo LC utilizado. As amostras com substratos de silício 1 e 2 consistem em duas partes:uma parte contém uma superfície mal estruturada e a segunda parte é uma superfície plana. Nessas amostras, temos a oportunidade de comparar a resposta não linear em uma célula plana (contendo uma parte plana do substrato de Si) e em uma célula microestruturada (contendo uma parte microestruturada do substrato de Si).

Dessa forma, em nossos experimentos, temos as seguintes células híbridas:

1)
abreviado M1:substrato de vidro + ITO / 5CB / substrato 1 de Si, superfície microestruturada
2)
abreviado F1:substrato de vidro + ITO / 5CB / Si substrato 1, superfície plana
3)
abreviado M2:substrato de vidro + ITO / 5CB / substrato 2 de Si, superfície microestruturada
4)
abreviado F2:substrato de vidro + ITO / 5CB / Si substrato 2, superfície plana
5)
abreviado M3:substrato de vidro + ITO / 5CB / Si substrato 3, superfície microestruturada
6)
abreviado M4:substrato de vidro + ITO / E7 / substrato 3 de Si, superfície microestruturada

Configuração experimental

A Figura 3 mostra o esquema da configuração experimental, que se baseia no método holográfico dinâmico com mistura de duas ondas. Semicondutor contínuo Nd:YAG laser (duplicação de frequência, λ =532 nm, P =52 mW, geração de modo único) é uma fonte de luz. Por meio de um divisor de feixe BS e um espelho M, a radiação laser é dividida em dois feixes B ₀ e B ₁ , convergindo na célula em um pequeno ângulo θ ≈ 0,01 rad. As intensidades de entrada I ₀ e eu ₁ são equalizados com a ajuda do filtro F1, e no nosso caso, I ₀ = eu ₁ =3,3 W / cm ² . O diâmetro de um ponto de laser em uma célula é de 1 mm.

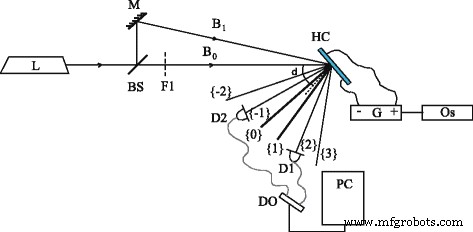
Esquema de configuração experimental:laser ( L ); espelho ( M ); divisor de feixe ( BS ); filtro óptico ( F1 ); vigas ( B ₀ ) e ( B ₁ ); fotodiodos ( D1 ) e ( D2 ); célula híbrida LC ( HC ); osciloscópio ( Os ); gerador ( G ); oscilografia digital ( DO ); computador ( PC ) As ordens de difração de saída são {0} e {1} as ordens principais; {−1} e {2} as primeiras ordens de difração; {−2} e {3} as segundas ordens de difração. δ é o ângulo de rotação da célula

Dois feixes de laser B ₀ e B ₁ formar um padrão de interferência dentro da amostra. Ambos os feixes incidentes têm p linear polarização. Assim, o padrão de interferência de modulação de intensidade é criado. A célula LC normal faz o ângulo δ com a bissetriz de B ₀ e B ₁ . O campo elétrico DC é aplicado devido à fonte G com a tensão U controlado na faixa de 0 a 15 V. O substrato de vidro ITO é definido como o eletrodo positivo. Medimos as intensidades das primeiras ordens de difração {−1} e {2} usando os fotodiodos D1 e D2 via osciloscópio digital controlado por computador DO. Os ângulos de rotação das células foram ajustados para maximizar o sinal de difração e pareceram ser δ ≈ 40 - 55 ⁰ para amostras diferentes. Esses resultados coincidem com os experimentos de outros grupos (por exemplo [9, 12]); a razão para tal efeito está além do escopo de nosso estudo.

Modelo de autodifração de ondas na aproximação de Raman-Nath

A autodifração de ondas foi considerada em vários trabalhos [17, 18]. Quando ocorre a autodifração de duas ondas de entrada na fina grade de índice de refração fotoinduzida, muitas ordens de difração aparecem na saída. Ao medir as intensidades nas primeiras ordens de difração, pode-se calcular a profundidade de modulação da rede ( Δn ) Uma vez que no meio semelhante a Kerr, a condição Δn = n ₂ eu ₀ é válido (onde eu ₀ é a intensidade do feixe de excitação), o coeficiente da refração não linear n ₂ é possível calcular.

Nesta seção, procuramos a solução para a eficiência de difração das primeiras ordens de difração no caso de grade de índice de refração senoidal não deslocada. Então, as intensidades em ordens simétricas serão iguais. A modelagem é iniciada a partir da equação de onda, na qual tanto o campo elétrico \ (\ overrightarrow {E} \) e a parte modulada da permissividade dielétrica Δε resultante do efeito não linear tipo Kerr depende da coordenada z (ao longo da propagação da onda):
$$ {\ nabla} ^ 2 \ overrightarrow {E} \ left (z, t \ right) =\ frac {1} {c ^ 2} \ frac {\ partial ^ 2} {\ partial {t} ^ 2} \ left [{\ varepsilon} _0 + \ varDelta \ varepsilon \ left (z, t \ right) \ right] \ overrightarrow {E} \ left (z, t \ right) $$ (1)
onde c é a velocidade da luz no vácuo, \ ({\ varepsilon} _0 ={n} _0 ^ 2 \) representa a permissividade dielétrica de um meio e n ₀ é o seu índice de refração. Buscaremos a solução da equação de onda (1) na soma de todas as ordens de difração, que são ondas planas polarizadas na direção do eixo \ (\ overrightarrow {y} \):
$$ \ overrightarrow {E} =\ frac {1} {2} \ overrightarrow {y} \ left \ {{\ displaystyle \ sum_ {m =- \ infty} ^ {+ \ infty} {\ overrightarrow {A}} _m \ left (z, t \ right) {e} ^ {i \ left [{\ omega} _0 t- \ left ({\ overrightarrow {k}} _ 0- m \ overrightarrow {K} \ right) \ overrightarrow { r} \ right]} {e} ^ {- \ frac {1} {2} \ alpha z} + c. c.} \ right \} $$ (2)
onde ω ₀ é a frequência da radiação laser, \ (\ overrightarrow {r} \) é a coordenada e “ c. c . ” denota o termo conjugado complexo. Em nossa representação, é conveniente expressar o coeficiente de atenuação como α = α _abs + α _sc , que leva em consideração as perdas de radiação laser tanto na absorção α _abs e espalhando α _s . A Figura 4 mostra o diagrama de vetor de onda de autodifração na aproximação de Raman-Nath. Isso demonstra que a onda do m -ésima ordem de difração corresponde à direção espacial descrita pelo vetor de onda \ ({\ overrightarrow {k}} _ m \). Ordens de difração m =0 e m =1 pertence a duas vigas emocionantes B ₀ e B ₁ . O vetor de onda do m -ésima ordem de difração é \ ({\ overrightarrow {k}} _ m ={\ overrightarrow {k}} _ 0- m \ overrightarrow {K} \), e \ (\ overrightarrow {K} \) é o vetor de onda de a grade fotoinduzida. A modulação de permissividade Δε é definido na forma de uma grade:
$$ \ varDelta \ varepsilon \ left (z, t \ right) =\ frac {1} {2} \ left [{\ overrightarrow {\ varepsilon}} _ 1 \ left (z, t \ right) {e} ^ { - i \ overrightarrow {K} \ overrightarrow {r}} + c. c. \ right] $$ (3)

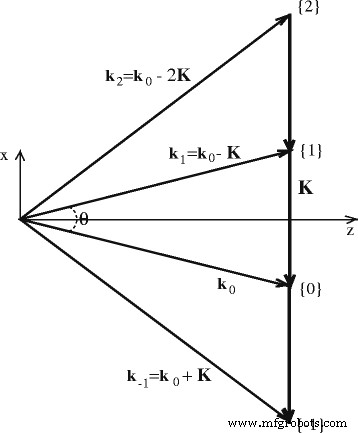
Diagrama de vetor de onda de autodifração de duas ondas coerentes (descrito por \ ({\ overrightarrow {k}} _ 0 \) e \ ({\ overrightarrow {k}} _ 1 \)) na aproximação de Raman-Nath

Substituindo a solução (2) e (3) na Eq. (1), obtém-se a relação para uma amplitude variável lenta A _m do m -ésima ordem:
$$ \ frac {\ partial {A} _m} {\ partial z} + i \ frac {\ left ({k} _0 ^ 2- {k} _m ^ 2 \ right)} {2 {k} _ {mz }} {A} _m- \ frac {1} {2} \ alpha \ cdot {A} _m =- i \ frac {k _ {\ upsilon} ^ 2} {4 {k} _ {mz}} \ left [ {\ varepsilon} _1 {A} _ {m + 1} + {\ varejpsilon} _1 ^ {*} {A} _ {m-1} \ right] $$ (4)
onde k _υ =2 π / λ é o vetor de onda no vácuo, e a marca “∗” denota a conjugação complexa. Visto que em nossa representação, os principais feixes de registro das ordens m =0 e m =1 são idênticos na entrada, bem como em toda a espessura da amostra, segue-se que ε ₁ é real e não depende da coordenada z (veja [18]):\ ({\ varepsilon} _1 (t) ={\ varepsilon} _1 ^ {*} (t) \). Para posterior transformação da Eq. (4), introduzimos uma nova função \ ({U} _m \ left (z, t \ right) ={A} _m \ left (z, t \ right) \ exp \ left (- \ frac {1} { 2} \ alpha z \ right) \ exp \ left (im \ frac {\ pi} {2} \ right) \), designar T =Exp (- αz ) as perdas de intensidade de luz no meio, e definir \ ({\ varepsilon} _1 =T {\ tilde {\ varepsilon}} _ 1 \). Ao introduzir uma nova variável \ (\ tilde {z} ={k} _ {\ upsilon} / \ left ({n} _0 \ cos \ left (\ theta / 2 \ right) \ right) \ cdot \ left (1 - T \ right) / \ left (2 \ alpha \ right) \), onde θ é o ângulo convergente, Eq. (4) pode ser escrito como:
$$ 2 \ frac {\ partial {U} _m} {\ partial \ tilde {z}} ={\ tilde {\ varepsilon}} _ 1 \ left [- {U} _ {m + 1} + {U} _ {m-1} - i \ frac {2 m \ left (m-1 \ right)} {\ phi} {U} _m \ right] $$ (5)
onde parâmetro ϕ é definido por \ (\ phi =T {\ tilde {\ varepsilon}} _ 1 / \ left (2 {n} _0 ^ 2 {\ sin} ^ 2 \ left (\ theta / 2 \ right) \ right) \) .

Nas condições da aproximação Raman-Nath, é possível negligenciar o último termo na parte direita da Eq. (5) (Ref. [18]), ou seja, 2 m ( m - 1) / ϕ <<1 para qualquer m . Então, introduzindo uma nova variável \ (\ zeta =\ tilde {z} {\ tilde {\ varepsilon}} _ 1 (t) \), obtemos nossa equação principal na aproximação de Raman-Nath:
$$ 2 \ frac {\ partial {U} _m \ left (\ zeta, t \ right)} {\ partial \ zeta} + {U} _ {m + 1} \ left (\ zeta, t \ right) - {U} _ {m-1} \ left (\ zeta, t \ right) =0 $$ (6)
Essa relação formalmente é uma representação bem conhecida para a função de Bessel, portanto, sua solução pode ser expressa por meio das funções de Bessel na forma:
$$ {U} _m \ left (\ zeta, t \ right) ={\ displaystyle \ sum_ {n =0} ^ {\ infty} {C} _n ^ m (t) {J} _n \ left (\ zeta \ direita)} $$ (7)
A Eq. (6) satisfaz propriedades de simetria \ ({U} _0 {U} _0 ^ {*} ={U} _1 {U} _1 ^ {*} \) para o par dos feixes principais, bem como para todos os pares dos feixes difratados (\ ({U} _2 {U} _2 ^ {*} ={U} _ {- 1} {U} _ {- 1} ^ {*} \)). Observe que em z =0, E ₀ (0, t ) = E ₁ (0, t ) ≠ 0, mas E _m (0, t ) =0 para m ≠ 0, 1 e, em seguida, intensidades de saída das primeiras ordens de difração I _{−1} ( d , t ) e eu _{2} ( d , t ) será igual e definido por uma fórmula (ver também [18]):
$$ {I} _ {\ left \ {- 1 \ right \}} \ left (d, t \ right) ={I} _ {\ left \ {2 \ right \}} \ left (d, t \ direita) =T {I} _0 \ esquerda (0, t \ direita) \ esquerda [{J} _1 ^ 2 \ esquerda (\ zeta \ direita) + {J} _2 ^ 2 \ esquerda (\ zeta \ direita) \ direita] $$ (8)
onde d é a espessura de um meio não linear; eu ₀ é a intensidade de um feixe de laser; J ₁ e J ₂ são as funções de Bessel do primeiro tipo da primeira e segunda ordens, respectivamente. Já que em nosso caso, as intensidades eu ₀ e eu ₁ são iguais, ou seja, 2 I ₀ = eu _laser , conseqüentemente, o valor de ζ pode ser escrito como:
$$ \ zeta =\ tilde {z} {\ tilde {\ varepsilon}} _ 1 =\ frac {k _ {\ upsilon}} {n_0 \ cdot \ cos \ left (\ theta / 2 \ right)} \ frac {1 - T} {2 \ alpha} {\ tilde {\ varepsilon}} _ 1 \ approx \ frac {k_0} {n_0} \ frac {1- T} {2 \ alpha} 2 {n} _0 \ varDelta n $$ ( 9)
Em um meio semelhante ao Kerr Δn = n ₂ eu ₀ , onde n ₂ representa o coeficiente de refração não linear, então o valor final de ζ tem uma forma mais simples:
$$ \ zeta =\ frac {2 \ pi} {\ lambda} \ frac {1- T} {\ alpha} {n} _2 {I} _0 $$ (10)
A eficiência de difração η da primeira ordem de difração é determinado como η = eu _{−1} / ( TI ₀ ) Por outro lado, a eficiência de difração pode ser obtida experimentalmente medindo a intensidade I _{−1} e o coeficiente de transmissão de uma célula T . A fórmula comum (8) é válida para calcular a eficiência de difração em uma grande faixa. Para menores eficiências de difração, η ≤ 2%, a boa aproximação será apenas o primeiro termo polinomial de (8): η ≈ ζ ² / 4. Consequentemente, pode-se obter uma relação simples para n ₂ :
$$ {n} _2 =\ frac {\ lambda} {\ pi} \ frac {\ alpha} {1- T} \ frac {\ sqrt {\ eta}} {I_0} $$ (11)
Deve-se notar que a Eq. Derivada (11) tem a mesma forma, como a equação que é convencionalmente obtida para o caso da difração de apenas um feixe de sonda de uma dada grade de índice de refração (ver, por exemplo, Ref. [19]). Mas para grandes valores de η , que é usual para células LC, uma relação mais precisa (8) e (10) deve ser usada para calcular os valores ζ e n ₂ .

Saber o valor n ₂ , pode-se definir a suscetibilidade não linear do meio com o auxílio da expressão:
$$ {\ chi} ^ {(3)} \ left [\ mathrm {esu} \ right] ={n} _2 \ left [\ frac {\ mathrm {c} {\ mathrm {m}} ^ 2} { W} \ right] \ cdot \ frac {9 \ cdot {10} ^ 4} {4 \ pi} c \ cdot {\ varepsilon} _e \ cdot {n} _0 ^ 2 $$ (12)
onde ε _e é a constante elétrica. No caso do nemático 5CB, usamos o índice de refração para a orientação homeotrópica das moléculas n ₀ = n _⊥ =1,51 como aquele do índice de refração comum; da mesma forma para a mistura nemática E7, n ₀ = n _⊥ =1,5268.

A abordagem teórica desenvolvida é válida para filmes finos que possuam não linearidade óptica tipo Kerr, quando as perdas de luz tanto na absorção quanto no espalhamento são grandes. Uma vez que o método de autodifração não requer uma fonte de laser adicional como uma sonda, a mistura de duas ondas torna-se um método simples para o diagnóstico de não linearidade óptica de meios finos, incluindo células LC.

Resultados e discussões

Sugerimos que o mecanismo óptico não linear em células híbridas LC seja um efeito fotorrefrativo induzido pela superfície, que altera a orientação das moléculas LC no volume iniciado a partir da superfície [12, 13]. Nos experimentos de mistura de duas ondas, a amostra é iluminada por um padrão de interferência de luz periódica formado por dois feixes de laser coerentes. Este padrão cria uma modulação de carga espacial na interface LC-substrato. A distribuição periódica resultante do campo elétrico na superfície estimula a modulação da orientação do diretor no substrato. A reorientação das moléculas começa na superfície e se espalha no volume LC.

O desempenho experimental típico de mistura de duas ondas com células LC híbridas é mostrado na Fig. 5. Na ausência de campo elétrico, observamos uma estrutura bidimensional regular dos feixes de laser principais refletidos de um substrato microestruturado da célula (Fig. 5a ) Após a aplicação da voltagem DC, muitas ordens de difração aparecem ao lado de cada par dos feixes principais devido à excitação da grade de índice de refração dentro da célula (Fig. 5b). No caso das células planas F1 e F2, não existe um padrão de multi-espalhamento, observamos apenas uma linha central após a aplicação da tensão. Medimos as intensidades nas primeiras ordens de difração {−1} e {+2} na linha central no estado estacionário para todas as células:células planas e células com superfície microestruturada. Em seguida, calculamos a eficiência de difração de acordo com η = Ī _{−1} / ( TI ₀ ), onde Ī _{−1} é a intensidade média das duas primeiras ordens de difração ( Ī _{−1} =( eu _{−1} + eu _{2} ) / 2) e T é o coeficiente de transmissão da célula.

Padrões típicos de espalhamento para dois feixes de laser interferentes formados por células LC não lineares híbridas com superfície microestruturada. a Padrão de dispersão de uma célula híbrida sem campo elétrico aplicado. b Formação de várias ordens de difração (a autodifração Raman-Nath) na aplicação de tensão elétrica DC. A linha central é mostrada em ( b ) por uma linha tracejada

Observe que o efeito fotorrefrativo induzido pela superfície, explorado em nossos experimentos, depende fortemente do ângulo de rotação da amostra em relação à bissetriz do ângulo de convergência entre duas ondas de entrada (ver, por exemplo, [9, 12, 13]). Assim, com a posição normal da amostra, quando a placa da amostra é perpendicular à bissetriz das ondas, nenhuma ordem de difração é observada. Ao mesmo tempo, em nosso caso, quando a amostra é girada em relação a essa bissetriz, a grade de índice de refração fotoinduzida parece ser deslocada em relação ao padrão de interferência de luz. Este efeito deve se manifestar na existência de transferência de energia entre ordens de difração. No caso de nossas células híbridas e dois feixes de laser com intensidades de entrada iguais, observamos que a diferença das intensidades nas primeiras ordens de difração não ultrapassa 10%. Tomamos um valor médio entre essas duas intensidades medidas que é usado para cálculos posteriores do coeficiente de refração não linear. Este valor pertence à faixa de precisão de nossas estimativas dos coeficientes ópticos não lineares. Observe também que o modelo matemático desenvolvido é reduzido a uma fórmula resultante bastante simples e não inclui as mudanças de fases da onda em um volume de uma camada não linear. O efeito da resposta não local no meio e a transferência de energia entre as ondas serão considerados cuidadosamente em nossos próximos trabalhos.

Na Tabela 1, reunimos os parâmetros experimentais medidos para as células híbridas LC. O coeficiente de transmissão é definido como T = eu ^fora / eu ₀ , onde eu ₀ é a intensidade de um único feixe incidente, e I ^fora é a intensidade do feixe de saída. T inclui duas partes: T = R _s T _a , onde R _s leva em consideração a perda de intensidade para espalhamento da superfície microestruturada para formar um padrão de luz periódico; e T _a =Exp (- αd _eff ) descreve a perda de intensidade na absorção durante a propagação da luz em uma grande quantidade de células LC. Na Tabela 1 também apresentamos os valores d _eff , que é uma espessura efetiva para um feixe de propagação em uma célula. Observe, em nossas medições, negligenciamos as perdas na reflexão da luz do limite do vidro de entrada de uma célula.

As eficiências de difração medidas para todas as células na dependência da voltagem aplicada são mostradas na Fig. 6. Pode-se ver que a eficiência de difração atinge seu máximo para uma determinada voltagem, que difere em várias células; esta tensão é maior para células microestruturadas em comparação com uma plana (compare F1 e M1, F2 e M2); bem como esta tensão é alterada na dependência de uma forma da microestrutura (compare M1, M2, M3, M4). Enfatizamos também que as eficiências de difração atingem valores bastante grandes em células LC (até 9% para as células M1 e F1). Usamos valores medidos de η para calcular as características ópticas não lineares das células LC investigadas, ou seja, o coeficiente de refração não linear n ₂ e suscetibilidade não linear efetiva χ ⁽³⁾ , levando em consideração que as células LC possuem não linearidade óptica semelhante a Kerr.

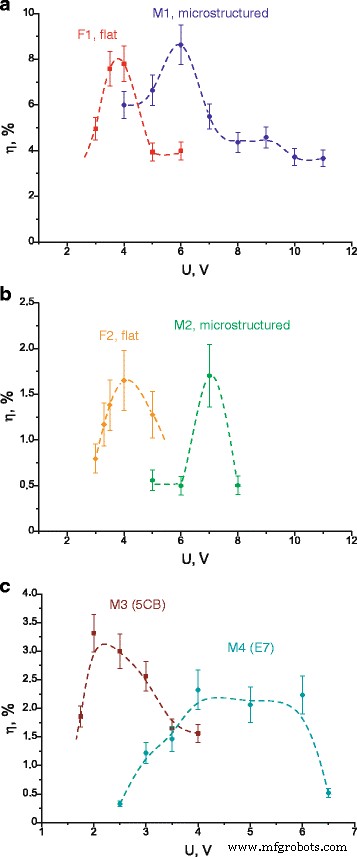
Eficiência de difração de primeira ordem de difração na dependência da tensão aplicada. a Células M1 e F1. b Células M2 e F2. c Células M3 e M4. Linhas tracejadas apresentado apenas para visualização

Coeficientes de refração não linear calculados a partir de medições experimentais das eficiências de difração são mostrados na Fig. 7 para todas as células. No caso das células M1 e F1, bem como M3 e M4, n ₂ é calculado a partir das fórmulas principais (8) e (10) como as eficiências de difração medidas η > 3,5%. Usamos a fórmula aproximada (12) para as células M2 e F2, conforme o obtido η <2%. Obtemos que o coeficiente máximo de refração não linear é maior em uma célula com substrato microestruturado em comparação com células planas (ver Fig. 7a, b). A Tabela 2 apresenta os valores de susceptibilidade não linear calculados a partir dos valores máximos de n ₂ na Fig. 7. A suscetibilidade não linear parecia estar essencialmente aumentada (em 30–100%) nas células com substrato microestruturado em relação às células feitas de substratos planos. Razões que levam ao aumento da profundidade de modulação da grade dinâmica nas células contidas em substratos microestruturados são o assunto para pesquisas futuras. Supomos que esse efeito esteja relacionado com a reorientação inicial das moléculas que surgem na superfície microestruturada.

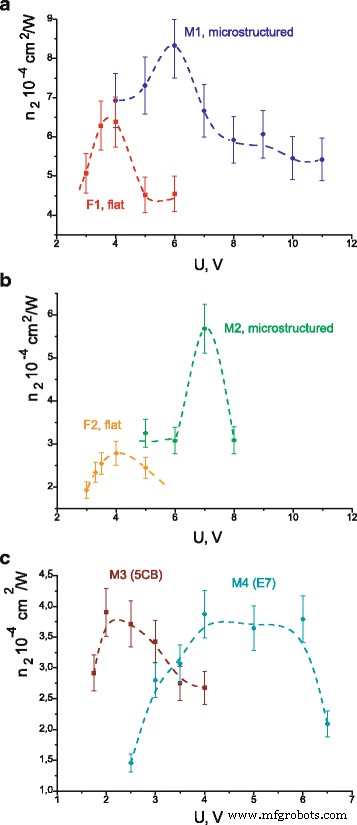
Coeficientes calculados de refração não linear em dependência da voltagem aplicada para células M1 e F1 ( a ); M2 e F2 ( b ); M3 e M4 ( c ) Linhas tracejadas são apenas para visualização

Conclusões

Nós investigamos o efeito óptico não linear em novas células híbridas LC baseadas em um cristal fotônico de silício. The cell consists of two different materials separated by a thin LC layer with homeotropic orientation of molecules. One material is a glass substrate with ITO electrode. The second one is silicon substrate with periodic microstructured surface. Microstructures in a shape of periodically arranged micro-pyramids are etched on the silicon surface by applying the chemical photolithography method or plasma etching one.

We apply the dynamic holography method with two-wave mixing to define the efficiency of self-diffraction of the dynamic grating induced in LC layer. A theoretical model for the Raman-Nath self-diffraction, offered for calculating the diffraction efficiency in the first diffraction orders, have allowed us to determine the nonlinear refraction coefficient n ₂ , and nonlinear susceptilibity χ ⁽³⁾ of the cells. We have also made a comparative analyses of nonlinear parameters obtained for cells with and without microstructures. Nonlinear susceptibility appeared to be essentially enhanced (by 30 − 100%) in the microstructured cells with respect to the cells made of flat surfaces. The underlying mechanism of the optical nonlinearity is the surface-induced photorefractive effect in the pure nematic LC. The increased modulation depth of the refractive index might be connected with initial reorientation of the molecules arising on the microstructured substrate.

The developed theoretical approach could be valid for determination of nonlinear optical characteristics of thin films possessing Kerr-like optical nonlinearity, in which the losses on the both absorption and scattering are large, as well as in the either transmission or reflection geometries. Photorefractive hybrid LC cells are perspective as new samples of electro-optical microsystems, including multi-channel SLMs. Additionally, two-wave mixing technique in such nonlinear cells may be successfully implemented in multi-channel couplers, switches, and optical communication lines. They may be also applied in networks, if to ensure the independent control of each channel in LCD structures.

Abreviações

5CB:: 4′-(n -pentyl)-4-cyanobiphenyl
E7:: Liquid crystal mixture
F1:: Hybrid LC cell, composed by flat part of Si plate 1/5CB/glass plate covered by ITO
F2:: Hybrid LC cell, composed by flat part of Si plate 2/5CB/glass plate covered by ITO
ITO:: Conductive layer of indium-tin-oxide
LC:: Cristais líquidos
M1:: Hybrid LC cell, composed by microstructured part of Si plate 1/5CB/glass plate covered by ITO
M2:: Hybrid LC cell, composed by microstructured part of Si plate 2/5CB/glass plate covered by ITO
M3:: Hybrid LC cell, composed by microstructured part of Si plate 3/5CB/glass plate covered by ITO
M4:: Hybrid LC cell, composed by microstructured part of Si plate 4/E7/glass plate covered by ITO
Si:: Silício

Detectando Exciton Espacialmente Localizada em Superredes de Pontos Quânticos Auto-Organizados InAs / InGaAs:Uma Forma de Melhorar a Eficiência Fotovoltaica Supercapacitores elásticos miniaturizados e lineares de alta taxa

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias