Barreiras Schottky e tipos de contato controláveis de tensão e campo elétrico em Graphene-MoTe2 van der Waals Heteroestrutura

Resumo

Os dichalcogenetos de metais de transição bidimensionais (2D) com superfícies intrinsecamente passivadas são candidatos promissores para dispositivos optoeletrônicos ultrafinos, pois seu desempenho é fortemente afetado pelo contato com os eletrodos metálicos. Aqui, cálculos de primeiro princípio são usados para construir e investigar as propriedades eletrônicas e interfaciais do MoTe 2D ₂ em contato com um eletrodo de grafeno, tirando o máximo proveito deles. Os resultados obtidos revelam que as propriedades eletrônicas do grafeno e MoTe ₂ as camadas são bem preservadas em heteroestruturas devido à fraca interação intercamada de van der Waals, e o nível de Fermi se move em direção à banda de condução mínima de MoTe ₂ camada formando assim um n digite contato Schottky na interface. Mais interessante, a altura da barreira Schottky e os tipos de contato no Graphene-MoTe ₂ a heteroestrutura pode ser efetivamente ajustada por deformação biaxial e campo elétrico externo, o que pode transformar a heteroestrutura de um n digite contato Schottky para um p digite um ou para contato ôhmico. Este trabalho fornece uma visão mais aprofundada para ajustar os tipos de contato e estratégias eficazes para projetar MoTe ₂ de alto desempenho com base em nanodispositivos eletrônicos Schottky.

Introdução

Cristais em camadas bidimensionais (2D) têm atraído interesse crescente devido às suas novas propriedades físicas e aplicações potenciais em vários campos desde a descoberta do grafeno [1]. Características e desempenho não convencionais, como o efeito Hall quântico meio-inteiro [2], tunelamento de Klein [3] e supercondutividade [4], foram descobertos em vários materiais 2D. Para o grafeno, no entanto, a estrutura de banda do tipo cone de Dirac sem um gap próximo ao nível de Fermi dificulta suas aplicações diretas em transistores. Isso tem estimulado a busca por materiais alternativos a partir de outros materiais 2D [5,6,7,8,9,10,11,12,13,14] com propriedades versáteis, entre as quais dichalcogenetos de metais de transição em camadas (TMDs) ganharam grande atenção . Os intervalos de banda de TMDs podem ser ajustados de cerca de 0,8 eV a 2,0 eV e são comparáveis aos de semicondutores convencionais, permitindo que TMDs sejam candidatos especialmente bons para aplicações optoeletrônicas. Por serem semelhantes ao grafite, a maioria dos TMDs são materiais de estrutura em camadas com interação de van der Waals (vdW) entre as camadas, portanto, podem ser esfoliados em poucas camadas ou em uma única camada [15, 16]. Verificou-se que os TMDs têm características dependentes da espessura e passariam por uma transição de gap indireto-direto [16, 17] quando eles são alterados de bulk para poucas camadas ou monocamada. Os TMDs de monocamada têm várias estruturas, como fases H e fases T (ou fases T ′), enquanto as fases H geralmente exibem características semicondutoras.

Como membro de TMDs, bulk MoTe ₂ inclui três fases interessantes:fase hexagonal (2H, semicondutora) [18], fase monoclínica (1 T ′, metálica) [19] e octaédrica (T _d , fase semimetal de Weyl tipo II [20, 21], em que a fase 2H é a mais estável. MoTe da fase 2H ₂ tem uma lacuna de banda indireta de cerca de 1,0 eV para bulk e uma lacuna de banda direta de cerca de 1,1 eV para monocamada [22, 23], o que indica que a lacuna de banda é quase independente do número de camadas e pode ser aplicada para o próximo - fotodetectores infravermelhos. Por conveniência, no texto a seguir, 2H-MoTe ₂ é simplesmente referido como MoTe ₂ . Comparado com outros TMDs, MoTe ₂ tem muitas vantagens, por exemplo, a condutividade é menor [24], o coeficiente de Seebeck é maior [24] e as habilidades de detecção são melhores [18, 25]. Combinando as vantagens do MoTe ₂ e grafeno, fabricando um tipo de heteroestrutura por grafeno e MoTe ₂ para aplicativos de dispositivo pode ser considerado. Na verdade, recentemente heteroestruturas verticais baseadas em materiais de estrutura em camadas 2D têm atraído interesses crescentes [26,27,28,29,30,31,32,33] devido à ausência de ligações pendentes nas superfícies de componentes isolados e fracos Fixação do nível femi. Para heteroestruturas verticais baseadas em grafeno-TMDs, os experimentos confirmaram sua excelente alta relação liga-desliga, alta foto-resposta, baixa corrente escura e boa eficiência quântica [34,35,36,37,38], em comparação com TMDs simples com base em tipos. Embora a maioria das heteroestruturas verticais baseadas em TMDs de grafeno sejam construídas com outros TMDs, como MoS ₂ , alguns experimentos investigaram o grafeno-MoTe ₂ heteroestrutura [39,40,41,42,43] devido às propriedades eletrônicas e ópticas únicas de MoTe ₂ . Foi relatado [39] que a relação liga-desliga do grafeno-MoTe ₂ a heteroestrutura vertical é tão alta quanto ~ (0,5 - 1) × 10 ⁻⁵ , e a capacidade de resposta da foto pode chegar a 20 mAW ⁻¹ , que são comparáveis aos valores correspondentes de grafeno-MoS ₂ dispositivo. Mais tarde, com base no grafeno-MoTe ₂ - heteroestrutura vdW vertical de grafeno, um fotodetector de infravermelho próximo foi fabricado [40, 42] com um desempenho superior, incluindo alta fotorresposta, alta eficiência quântica externa, resposta rápida e processos de recuperação e livre de uma fonte externa de fonte de alimentação de dreno em comparação com outros fotodetectores de semicondutores em camadas. Então, um grafeno-MoTe ₂ O transistor vertical vdW que exibe características ambipolares em forma de V adequadas [41] foi relatado. Conseqüentemente, o grafeno-MoTe ₂ heteroestruturas são candidatos promissores para nanodispositivos optoeletrônicos com alta responsividade, alta velocidade e flexível. Nesse sentido, é essencial realizar uma investigação teórica sobre o grafeno-MoTe ₂ heteroestrutura vertical que não foi relatada ainda.

Para a heteroestrutura metal-semicondutor, o tipo de contato (contato Schottky ou contato ôhmico) deve ser considerado, pois determina a existência de características retificadoras ou não para a heteroestrutura. Para o contato Schottky, a altura da barreira Schottky (SBH) teria um papel fundamental no comportamento dos dispositivos correspondentes [44] e tem sido investigada intensamente. A fim de obter alto desempenho para as aplicações reais do dispositivo, seria desejável que o SBH pudesse ser ajustado. Muitas estratégias têm sido propostas para modular a SBH, entre as quais a aplicação de um campo elétrico externo e deformação biaxial são as formas mais comuns.

Neste artigo, com base em cálculos de primeiros princípios, estrutura eletrônica e campo eletrônico externo e dependência de deformação do SBH de grafeno-MoTe ₂ heteroestruturas foram investigadas. Os resultados calculados demonstram que as propriedades eletrônicas do grafeno e MoTe ₂ monocamada são preservadas muito bem depois de serem empilhadas verticalmente como uma heteroestrutura. A barreira Schottky da heteroestrutura pode ser alterada entre p digite e n digite aplicando um campo elétrico externo ou deformação, e a heteroestrutura pode até alcançar o contato ôhmico quando o campo elétrico externo ou deformação é forte o suficiente.

Métodos Computacionais

Cálculos de primeiro princípio foram realizados usando o Vienna Ab-initio Simulation Package (VASP) [45,46,47] com base na teoria do funcional da densidade (DFT). Os pseudopotenciais do projetor de onda aumentada (PAW) [48] foram aplicados para modelar a interação íon-elétron e a aproximação de gradiente generalizado de Perdew-Burke-Ernzerhof (PBE) (GGA) [49] para tratar a correlação de troca de elétrons. Para todos os cálculos, o método DFT-D2 [50] de Grimme representando o termo de interação vdW é empregado e a energia de corte da onda plana é definida como 600 eV. O limite de convergência é definido para 10 ⁻⁶ eV para energia e 0,01 eV / Å para força. A zona de Brillouin k a malha de pontos é definida como 9 × 9 × 1 no esquema Monkhost-Pack. Um espaço de vácuo de 25 Å ao longo do z direção é adotada para evitar a interação entre as camadas vizinhas. Como foi revelado que o efeito de acoplamento spin-órbita em estruturas de banda de 2H-MoTe ₂ é muito fraco [51], todos os cálculos não consideram o acoplamento spin-órbita.

O grafeno-MoTe ₂ heteroestrutura é construída por grafeno e MoTe ₂ monocamada através do empilhamento dos dois materiais 2D ao longo da direção vertical. Grafeno e MoTe ₂ adote a rede hexagonal e seus parâmetros de rede são 2,46 Å [52] e 3,52 Å [53], respectivamente. Portanto, a incompatibilidade de rede é menor do que o critério anterior de 5%. De acordo com as estruturas de grafeno e MoTe ₂ monocamada, aqui, três modos de empilhamento típicos são considerados:HS-1, HS-2 e HS-3, que são mostrados na Fig. 1. Para o modo de empilhamento HS-1, um átomo de Te localiza-se apenas sob o local oco do rede de grafeno; para HS-2, um átomo de Te fica sob um sítio de átomo C da rede de grafeno; para HS-3, um átomo de Te fica sob outro sítio de átomo C não equivalente da rede de grafeno.

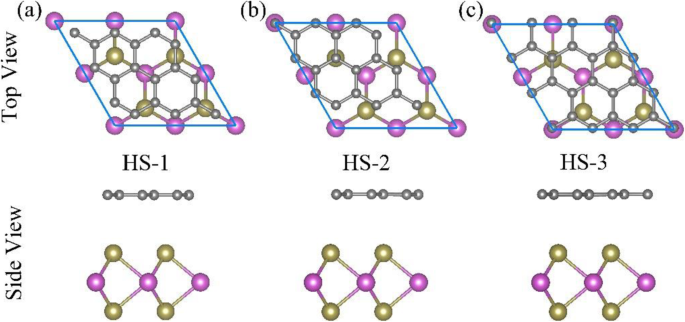
Vista superior e vista lateral de três modos de empilhamento típicos para o grafeno-MoTe ₂ heteroestrutura:( a ) HS-1, ( b ) HS-2, ( c ) HS-3. As bolas cinza, rosa e verde representam os átomos de carbono, molibdênio e telúrio, respectivamente

Quando a dependência da deformação do SBH é investigada, a deformação é aplicada igualmente ao longo das direções em zigue-zague e poltrona do grafeno, respectivamente.

Resultados e discussão

As estruturas de cristal de rede para MoTe ₂ monocamada e três modos de empilhamento típicos (HS-1, HS-2 e HS-3) do grafeno-MoTe ₂ heteroestrutura foram totalmente otimizados. As energias de ligação obtidas dos três modos de empilhamento típicos são quase iguais, ou seja, -0,85 eV, enquanto as distâncias entre camadas de equilíbrio dos três modos são todas aproximadamente iguais a 3,53 Å. Portanto, nos concentramos exclusivamente no grafeno-MoTe HS-1 ₂ heteroestrutura para a discussão a seguir e omite "HS-1" para simplificar no texto a seguir. As estruturas geométricas otimizadas de MoTe ₂ monocamada e grafeno-MoTe ₂ heteroestrutura são mostradas na Fig. 2. Obviamente, MoTe ₂ a monocamada adota a rede hexagonal e a constante de rede otimizada é 3,52 Å, o que é consistente com os resultados do experimento [53, 54]. Isso pode ser visto claramente na estrutura de bandas do MoTe ₂ monocamada, como é mostrado na Fig. 3, que MoTe ₂ monocamada é um semicondutor com um gap de 1,14 eV, o que também é consistente com os resultados do experimento [22, 23]. Quando grafeno e MoTe ₂ monocamadas são empilhadas verticalmente como uma heteroestrutura, a distância entre camadas de equilíbrio é 3,53 Å, que é comparável ao valor de Sb-MoTe ₂ heteroestrutura (cerca de 3,94 Å) [55]. Também pode ser visto na Fig. 2 que as estruturas geométricas do MoTe ₂ camada e camada de grafeno no Graphene-MoTe ₂ a heteroestrutura quase permanece a mesma que as estruturas originais de MoTe ₂ monocamada e grafeno, o que indica que a interação entre essas duas camadas é fraca. A energia de ligação das estruturas de equilíbrio -0,85 eV é menor do que a do Sb-MoTe ₂ heteroestrutura (cerca de −0,37 eV) [55], então a heteroestrutura é energeticamente estável. Tanto a distância de equilíbrio entre duas camadas quanto a energia de ligação são comparáveis àquelas de heteroestruturas baseadas em grafeno vdW típicas, como carboneto de fósforo hidrogenado de grafeno [56], grafeno-AsSb [29], grafeno-SMoSe e grafeno-SeMoS [30] , e grafeno-fosforeno [57], indicando que a interação entre MoTe ₂ e o grafeno é do tipo vdW fraco.

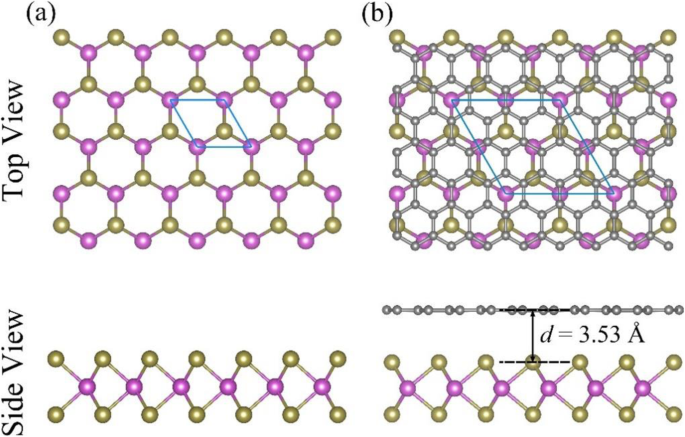
Vista superior e vista lateral das estruturas otimizadas de ( a ) MoTe ₂ monocamada e ( b ) grafeno-MoTe ₂ heteroestrutura. As bolas cinza, rosa e verde representam os átomos de carbono, molibdênio e telúrio, respectivamente. Os paralelogramos azuis denotam as células unitárias 2D

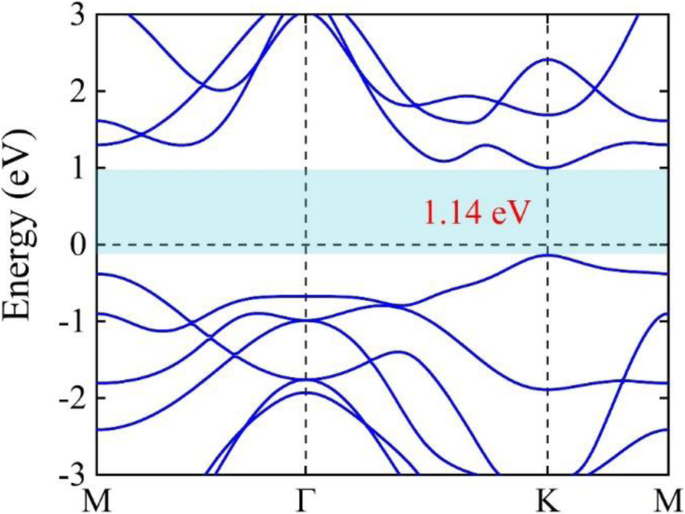
Estrutura de banda eletrônica de MoTe ₂ monocamada. A região azul claro representa o gap entre as bandas de valência e condução

Na verdade, a redistribuição e transferência de carga ocorreria inevitavelmente quando o grafeno e MoTe ₂ monocamadas são empilhadas para formar a heteroestrutura. A diferença de densidade de carga 3D no grafeno-MoTe ₂ heteroestrutura definida como Δ ρ = ρ _H - ρ _G - ρ _MT foi calculado, onde ρ _H , ρ _G e ρ _MT são as densidades de carga da heteroestrutura, grafeno isolado e MoTe ₂ monocamada, respectivamente. O resultado é mostrado na Fig. 4a, na qual as regiões azul e rosa escuro representam o acúmulo e o esgotamento de carga, respectivamente. Obviamente, a região azul está logo abaixo do MoTe ₂ camada, que indica que os elétrons se acumulam em torno do MoTe ₂ camada; enquanto a camada de grafeno é circundada pela área rosa escura, implicando que os buracos se acumulam em torno da camada de grafeno. Para ver a propriedade da transferência de carga mais claramente, a média planar 〈∆ ρ 〉, Que é definido como o valor médio da diferença de densidade de carga 3D Δ ρ em aviões com z =const. que são paralelas à camada de grafeno, é mostrado como uma linha azul na Fig. 4a, onde os valores negativos e positivos representam a depleção e o acúmulo de elétrons, respectivamente. O resultado verifica que alguns elétrons são transferidos da camada de grafeno para MoTe ₂ camada, e há oscilações em 〈 ∆ρ 〉 No grafeno e MoTe ₂ camada. A função de localização de elétrons (ELF) também é representada graficamente na Fig. 4b, a partir da qual pode ser visto que a forma de ELF em torno do átomo de Te perto da camada de grafeno é obviamente diferente daquela em torno do átomo de Te do outro lado, sugerindo que existência de interação vdW interlayer na heteroestrutura.

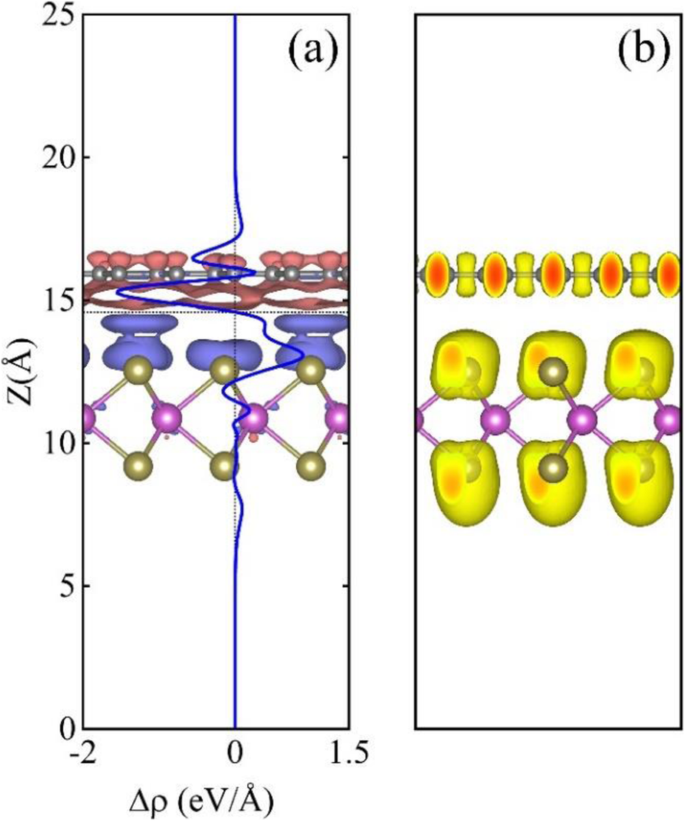
a A diferença de densidade de carga 3D e a diferença de densidade de carga média (linha azul) como uma função da posição no grafeno-MoTe ₂ heteroestrutura ao longo do z direção, onde as regiões azul e rosa escuro denotam o acúmulo e deficiência de elétrons, respectivamente. A linha tracejada horizontal marca a localização central entre a camada de grafeno e MoTe ₂ camada. b Função de localização de elétrons do grafeno-MoTe ₂ heteroestrutura com o isovalor de 0,7

Muitas propriedades físicas são determinadas pelas estruturas de banda e densidade de estados (DOS), e as estruturas de banda calculadas e DOS do grafeno-MoTe ₂ as heteroestruturas são mostradas na Fig. 5, onde o nível de Fermi é definido como zero. O cone de Dirac da camada de grafeno ao redor do nível de Fermi ainda está bem preservado; entretanto, um gap de banda de cerca de 10,6 meV é aberto. Ou seja, há um acoplamento intercalar pequeno, mas perceptível na heteroestrutura. As bandas contribuídas pelo MoTe ₂ camada demonstra que as características do semicondutor de MoTe ₂ camada com uma lacuna de banda direta são retidos. A diferença de banda de MoTe ₂ camada é de 0,85 eV na heteroestrutura, que é alterada em comparação com o resultado de 1,14 eV para o MoTe isolado ₂ monocamada. Uma característica marcante na Fig. 5 é que a estrutura da banda pode ser considerada como a simples soma das bandas das camadas isoladas. Não é surpreendente que a interação entre a camada de grafeno e o MoTe ₂ camada é insuficiente para modificar as características da estrutura de banda de cada componente na heteroestrutura, de modo que o efeito de interação intercamada na estrutura de banda é muito fraco. Isso indica ainda que a interação vdW domina entre MoTe ₂ camada e camada de grafeno na heteroestrutura, preservando assim as propriedades intrínsecas da chave.

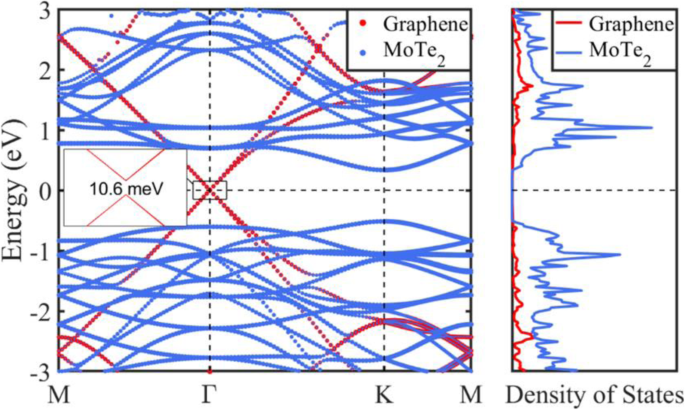
Estruturas de banda e densidade parcial de estados da camada de grafeno e MoTe ₂ camada no grafeno-MoTe ₂ heteroestrutura

As propriedades de contato de heteroestruturas são importantes para aplicações de dispositivos. Um grafeno-MoTe ₂ transistor baseado em heterojunção foi projetado, e o diagrama esquemático é mostrado na Fig. 6a, onde o MoTe ₂ monocamada é usada como o material do canal e o grafeno como fonte ou dreno e eletrodos de porta. Devido à diferença nas funções de trabalho do metal e do semicondutor, há uma curvatura de banda na interface, que pode ser estimada pela diferença de nível de Fermi (Δ E _F ), definido por Δ E _F = W _{G - MT} - W _MT , onde W _{G - MT} e W _MT são as funções de trabalho das heteroestruturas e o MoTe ₂ correspondente monocamada, respectivamente. O W calculado _{G - MT} e W _MT são 4,36 eV e 4,84 eV, respectivamente, conforme mostrado na Fig. 6b. Os resultados são consistentes com os valores experimentais [39]. Consequentemente, a curvatura da banda (Δ E _F ) é cerca de 0,48 eV na heteroestrutura, que é comparável ao resultado da heteroestrutura de carboneto de fósforo hidrogenado com grafeno [56].

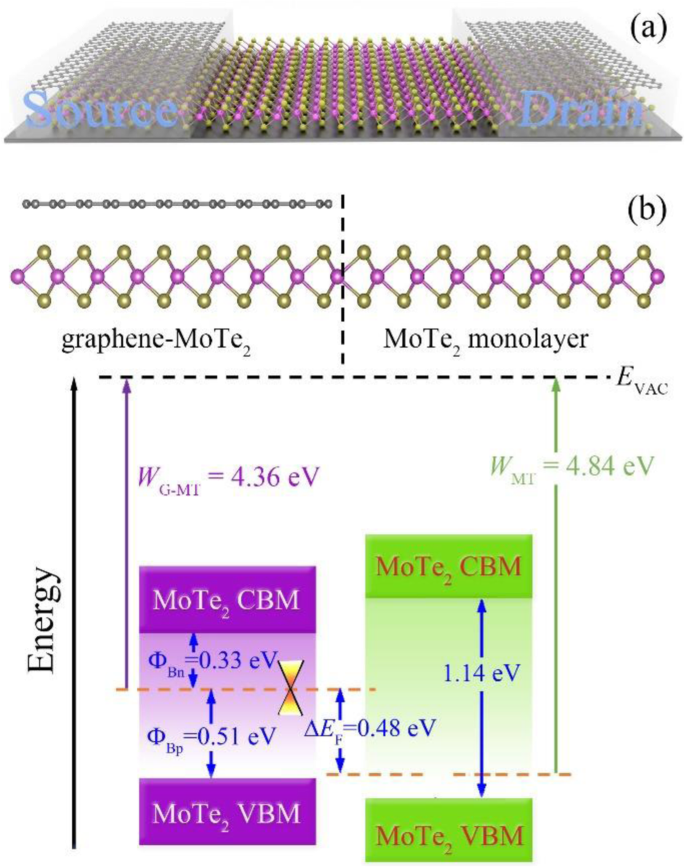
a O diagrama esquemático de um grafeno-MoTe ₂ transistor baseado em heteroestrutura. b Alinhamento de banda de grafeno-MoTe ₂ heteroestrutura com relação ao nível de vácuo, onde o cone vermelho representa a posição do ponto de Dirac da camada de grafeno na heteroestrutura. CBM e VBM representam o mínimo da banda de condução e o máximo da banda de valência, respectivamente. W _G-MT e W _MT são as funções de trabalho do Graphene-MoTe ₂ heteroestrutura e MoTe ₂ monocamada, respectivamente

Uma das propriedades de contato mais importantes das heteroestruturas semicondutoras de metal é a barreira Schottky na interface vertical (entre a camada de grafeno e o MoTe ₂ camada), que determina o fluxo de corrente através da interface de heteroestruturas, desempenhando assim um papel significativo no desempenho do dispositivo correspondente. Em geral, de acordo com os tipos de semicondutores em heteroestruturas, SBH é dividido em n digite e p tipo, respectivamente. O n tipo SBH ( Φ _Bn ) é definido como a diferença de energia entre o mínimo da banda de condução (CBM) do semicondutor ( E _C ) e o nível de Fermi do metal ( E _F ), ou seja, Φ _Bn = E _C - E _F . O p tipo SBH ( Φ _Bp ) é definido como a diferença de energia entre o nível de Fermi do metal e a banda de valência máxima (VBM) do semicondutor ( E _V ), ou seja, Φ _Bp = E _F - E _V . Os resultados SBH do grafeno-MoTe ₂ a heteroestrutura é mostrada na Fig. 6b. Devido à transferência de carga, o nível de Fermi se move do lado da banda de valência do MoTe ₂ monocamada para o lado da banda de condução de MoTe ₂ camada na heteroestrutura, o que denota que o SBH da heteroestrutura é n digite com o valor de cerca de 0,33 eV na interface. Ou seja, a condução de carga da heteroestrutura será principalmente por meio de elétrons.

Para melhorar o desempenho de transistores baseados em heteroestrutura, seria desejável sintonizar o SBH. É demonstrado que o SBH pode ser ajustado através da aplicação de um campo elétrico externo e deformação no plano [29, 30, 58]. Uma série de cálculos para a estrutura de banda da heteroestrutura sob diferentes campos elétricos externos foram feitos, e os resultados são mostrados na Fig. 7, onde a direção para o campo elétrico externo positivo aponta de MoTe ₂ camada para a camada de grafeno, enquanto o valor negativo é ao longo da direção oposta. Na região de contato Schottky, Φ _Bn exibe uma relação aproximadamente linear ascendente com o campo elétrico, enquanto Φ _Bp se comporta de forma inversa. Esses resultados sugerem que os campos elétricos positivos e negativos permitem que o nível de Fermi mude em direção ao VBM e CBM do MoTe ₂ camada na heteroestrutura, respectivamente. Sob o campo elétrico negativo, Φ _Bn é menor que Φ _Bp o tempo todo, indicando que a barreira Schottky é n modelo. Quando o campo elétrico positivo é um pouco maior que zero, Φ _Bn começa a ser maior que Φ _Bp , o que significa que a barreira Schottky foi alterada de n digite p digite no grafeno-MoTe ₂ interface. É óbvio que o gap (aproximadamente igual à soma de Φ _Bn e Φ _Bp ) do MoTe ₂ camada quase permanece constante sob o campo elétrico externo, o que denota que o campo externo tem pouco efeito nas propriedades eletrônicas primitivas. Isso pode ser entendido da seguinte forma:embora o campo elétrico externo possa alterar os autovalores de energia do elétron de valência, como CBM e VBM, seus valores relativos permanecem inalterados, resultando no gap permanecendo constante. Em outras palavras, o campo elétrico externo não poderia alterar a estrutura da banda, exceto a curvatura da banda. Também pode ser visto claramente na Fig. 7 que o SBH torna-se negativo quando o campo elétrico positivo é maior que 1,0 V / nm, o que significa que os elétrons do grafeno seriam injetados em MoTe ₂ sem qualquer barreira, indicando que MoTe ₂ possui uma condutividade metálica, realizando assim uma transição de contato Schottky-para-ôhmico. Para o campo elétrico negativo quando a intensidade excede 1,0 V / nm, a heteroestrutura também pode ser sintonizada com o contato ôhmico. Todos esses resultados demonstram que a aplicação de um campo elétrico externo é uma estratégia eficaz para modular o SBH e o tipo de contato para o grafeno-MoTe ₂ heteroestrutura.

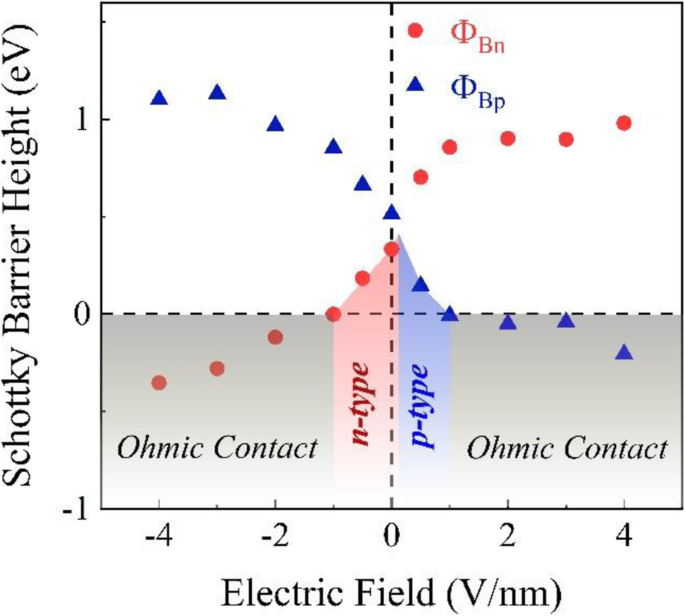
A altura da barreira Schottky do grafeno-MoTe ₂ heteroestrutura em função do campo elétrico externo. As áreas azuis e vermelhas denotam o contato Schottky como p digite e n tipo, respectivamente. A área cinza marca a região de contato ôhmico

O SBH como uma função da deformação biaxial no plano também é calculado e os resultados são exibidos na Fig. 8. Para a aplicação da deformação biaxial, o z As coordenadas dos átomos de Te são relaxadas enquanto as posições dos outros átomos permanecem fixas após a mudança do tamanho da célula unitária. É mostrado que a deformação também pode sintonizar o SBH da heteroestrutura entre n digite e p digite e conduza a heteroestrutura para se aproximar do contato ôhmico. Os comportamentos de dependência de deformação de SBH são muito diferentes daqueles da dependência de campo elétrico. A situação se torna muito mais complexa. Para uma ampla faixa de deformação, Φ _Bn é menor que Φ _Bp , embora apenas em uma faixa estreita de deformação de tração Φ _Bp mantém-se menor que Φ _Bn . Ou seja, a faixa de deformação de n -tipo SBH (a cepa é de cerca de −10 ~ 4%) é muito mais amplo do que o de p tipo (cerca de 4 ~ 7%). Quando a deformação de tração atinge 7% e a deformação compressiva atinge 10%, o contato ôhmico para a heteroestrutura também aparece. É importante notar que o gap do MoTe ₂ camada na heteroestrutura mudaria fortemente com a variação da deformação na região de contato Schottky, que é fortemente diferente com os resultados do caso de campo elétrico. Quando as redes estão sob tensão, elas se desviam do estado de equilíbrio, causando a mudança na estrutura da banda. Na verdade, não apenas o valor do gap, mas também o tipo de gap (direto ou indireto) seria alterado pela deformação. Para pequenas tensões, MoTe ₂ camada permanece uma lacuna de banda direta enquanto muda para lacuna de banda indireta para grande deformação. Aqui, deve ser apontado que para um transistor real as condições reais para realizar a transição de contato Schottky-para-Ohmic podem ser um pouco diferentes com os resultados calculados devido às situações reais.

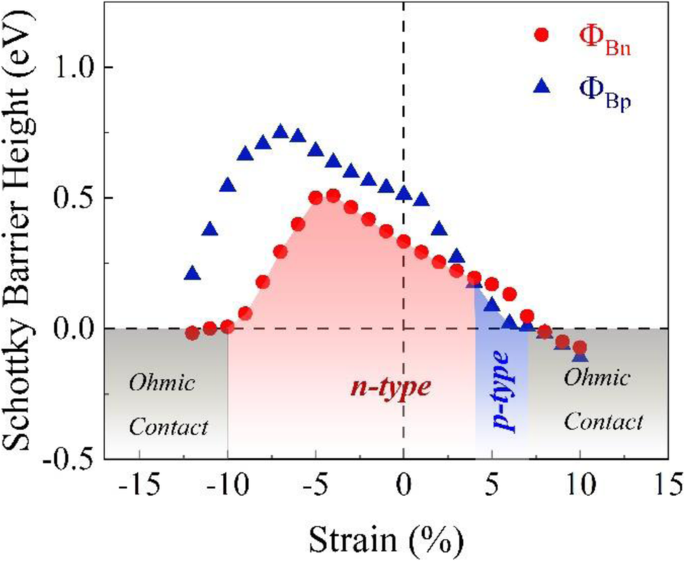
A altura da barreira Schottky do grafeno-MoTe ₂ heteroestrutura em função da deformação. As áreas azuis e vermelhas denotam o contato Schottky como p digite e n tipo, respectivamente. A área cinza marca a região de contato ôhmico

Os resultados acima sugerem que tanto a aplicação de um campo elétrico externo quanto a deformação biaxial no plano são métodos eficazes para controlar SBH e o tipo de contato do grafeno-MoTe ₂ heteroestrutura, que é indispensável para projetar transistores de efeito de campo baseados em heteroestrutura 2D vdW. Além disso, o grafeno-MoTe ₂ a heteroestrutura pode ser aplicada para diodos Schottky sintonizáveis em dispositivos nanoeletrônicos e optoeletrônicos.

Conclusões

Em resumo, as estruturas de banda do grafeno-MoTe ₂ heteroestrutura sob diferentes campos elétricos e deformações biaxiais têm sido investigadas sistematicamente com base em cálculos de primeiro princípio. As estruturas eletrônicas do grafeno e MoTe ₂ são bem preservados após serem empilhados juntos ao longo da direção vertical, o que sugere que a interação intercamada da heteroestrutura pertence ao tipo vdW. No entanto, o nível Fermi se move em direção ao CBM do MoTe ₂ camada após a formação da heteroestrutura, ou seja, os contatos Schottky são n tipo com um SBH de 0,33 eV. O SBH e o tipo de contatos na interface da heteroestrutura podem ser modulados de forma eficaz pela aplicação de um campo elétrico externo ou deformação. Quando um campo elétrico é aplicado, na região de contato Schottky, o n o tipo SBH exibe uma relação linear aproximadamente ascendente com o campo elétrico, e p tipo SBH se comporta inversamente. A heteroestrutura pode ser ajustada para o contato ôhmico para um campo elétrico maior que 1,0 V / nm em ambos os lados positivo e negativo. Para o caso da aplicação de deformação biaxial, a situação é mais complexa do que para o caso do campo elétrico. A faixa de deformação de n tipo SBH é muito mais amplo do que p modelo. Quando a deformação de tração atinge 7% ou a deformação compressiva atinge 10%, o contato ôhmico também aparece. Todos os resultados demonstram que a aplicação de um campo elétrico ou deformação é uma boa forma de controlar o SBH bem como o tipo de contato da heteroestrutura, podendo inclusive conduzir o sistema ao contato ôhmico. Esses recursos são bastante significativos para o projeto de dispositivos nanoeletrônicos e optoeletrônicos de alto desempenho.

Disponibilidade de dados e materiais

Os conjuntos de dados que suportam as conclusões deste artigo estão incluídos no artigo, e mais informações sobre os dados e materiais podem ser disponibilizados ao interessado mediante solicitação motivada dirigida ao autor correspondente.