Mecanismo de deformação de subsuperfície em nanocorte de arseneto de gálio usando simulação de dinâmica molecular

Resumo

Durante o processo de nano corte, o arsenieto de gálio monocristalino é confrontado com várias deformações e danos na superfície / subsuperfície que influenciam significativamente o desempenho do produto. Neste artigo, simulações de dinâmica molecular de nano corte em arseneto de gálio são conduzidas para investigar o mecanismo de deformação superficial e subsuperficial. Os deslocamentos são encontrados na subsuperfície usinada. A transformação de fase e a amorfização são estudadas por meio de números de coordenação. Os resultados revelam a existência de uma fase intermediária com um número de coordenação de cinco durante o processo de corte. Modelos com diferentes velocidades de corte são estabelecidos para investigar os efeitos no deslocamento. O efeito da anisotropia de cristal no tipo de deslocamento e densidade é estudado por meio de modelos com diferentes orientações de corte. Além disso, a tensão de subsuperfície também é analisada.

Introdução

O arsenieto de gálio (GaAs) é um tipo típico de composto III-V e também um dos materiais semicondutores mais importantes. Favorecido por suas grandes propriedades, como bandgap direto, alta mobilidade de elétrons e alta resistividade, o arseneto de gálio monocristalino encontra ampla aplicação em várias áreas, como dispositivos ópticos infravermelhos e dispositivos de micro-ondas. Com o desenvolvimento contínuo de sua produção, os requisitos estritos de rugosidade da superfície, precisão da forma da superfície e danos subterrâneos são cada vez mais exigidos. A tecnologia de nanocorte é benéfica para melhorar o desempenho dos elementos ópticos de arseneto de gálio e expandir o campo de suas aplicações. O processo de nanocorte do cristal de arseneto de gálio enfrenta muitas dificuldades, como rachaduras quebradiças, anisotropia e outros danos subterrâneos. Portanto, o estudo do mecanismo de nano corte do arseneto de gálio é de grande importância na solução dos problemas de usinagem, melhorando a qualidade da superfície do arseneto de gálio e desenvolvendo a tecnologia de processamento nanométrica relacionada.

Muitos estudos realizaram experimentos em nanoescala com arsenieto de gálio. Fang et al. [1] comparou as características de nanoindentação e nanoscratch de arsenieto de gálio e silício. Taylor et al. [2] investigaram as nanoindentações de carga ultrabaixa em arsenieto de gálio (100) com uma ponta de canto em cubo. Bradby et al. [3] encontraram os eventos pop-in do arsenieto de gálio em uma reentrância esférica. Fang et al. [4, 5] investigaram as propriedades de usinagem de semicondutores frágeis e moles e obtiveram a superfície do espelho de arsenieto de gálio pela primeira vez por torneamento de diamante. Embora muitos estudos sobre indentação e propriedades físicas do arseneto de gálio tenham sido relatados, pouco se sabe sobre seu processo de nano corte e o mecanismo de formação de danos. Isso se deve principalmente à grande dificuldade em conduzir os experimentos e subsequentes caracterizações. Por outro lado, é quase impossível inspecionar o processo de nano corte e medir os dados nanométricos usando medição on-line devido à escala nanométrica e à alta velocidade de corte. Por outro lado, é caro conduzir uma série de experimentos de usinagem e medição nanométrica.

A simulação de dinâmica molecular (MD) é um dos métodos mais eficientes para explorar o mecanismo de usinagem nanométrica. Shimada et al. [6, 7] provaram que a simulação MD é uma forma eficaz de descrever o processo de usinagem nanométrica. Komanduri et al. [8] encontraram o fenômeno de transição estrutural do silício no processo de nano corte com simulação MD. Pei et al. [9] estudaram a formação de deslocamento de cobre com os modelos MD em larga escala de usinagem nanométrica. Lai et al. [10] estudaram os efeitos do ângulo de ataque crítico e da deformação do material de germânio no corte nanométrico e, além disso, investigaram o processo de nano corte parcialmente sobreposto [11]. Além disso, a abordagem de modelagem multiescala se desenvolveu muito na área de usinagem de ultraprecisão [12,13,14]. A simulação multiescala combina métodos de simulação em diferentes escalas, como o modelo MD em nanoescala e o modelo FE em nano / micro escala [15], para estudar o processo de usinagem de forma mais abrangente e realista. Neste artigo, o mecanismo de deformação subsuperficial do processo de nano-corte é enfocado, portanto a simulação MD é selecionada como método de pesquisa.

Quanto aos materiais estudados, a maioria dos estudos de simulação de MD em usinagem nanométrica enfoca os elementos semicondutores como silício e germânio ou metais como cobre e alumínio. Poucos estudos foram relatados sobre a análise numérica em nano corte de arseneto de gálio. Fan et al. [16] investigaram a resposta dúctil do arsenieto de gálio por simulação MD e experimentos de torneamento. Yi et al. [17] estudaram a transformação de fase e anisotropia do arseneto de gálio no processo de nanoscratch via simulação MD. Neste trabalho, uma série de simulações tridimensionais de MD são realizadas para investigar a deformação dúctil no processo de nanocorte em arseneto de gálio monocristalino. O efeito dos parâmetros de corte, como velocidade de corte e orientação de corte, também são estudados sistematicamente.

Métodos

Modelos de simulação MD são estabelecidos para estudar o comportamento de deformação do cristal frágil de arsenieto de gálio no processo de nano-corte. O modelo de simulação tridimensional MD é mostrado na Fig. 1. A peça é construída como arsenieto de gálio monocristalino, cristalizando na rede de zincblenda com átomos de Ga e As ocupando as duas sub-redes FCC. O tamanho da peça é 85 nm × 30 nm × 35 nm. O modelo da peça consiste em três camadas:camada limite, camada termostática e camada newtoniana. A peça de trabalho é fixada pela camada limite, enquanto a camada termostática é definida a uma temperatura constante de 293 K para imitar a dissipação de calor no processo de usinagem real. A camada newtoniana é a área de corte que revelará o mecanismo do processo de nano corte. Os movimentos dos átomos na camada newtoniana obedecem à segunda lei de Newton clássica. Para imitar a ferramenta de diamante no processo de corte real, um modelo de ferramenta de diamante hemisférico com um raio de aresta de ferramenta de 10 nm é construído e a profundidade de corte é definida como 4 nm. A ferramenta de diamante é ajustada em certas velocidades para cortar a peça de trabalho. Com a limitação do recurso de computação, o modelo é minimizado e simplificado, mas ainda é convincente para explicar a deformação dúctil e formação de danos em escala nanométrica. A ferramenta de diamante é simplificada como um hemisfério para estudar os comportamentos de remoção dúctil na direção horizontal como fluxo lateral e empilhamento nos dois lados da ferramenta, que são as características importantes da simulação tridimensional. Para estudar o efeito dos parâmetros do processo, são construídos modelos com diferentes velocidades e orientações de corte. A Tabela 1 lista os parâmetros dos modelos.

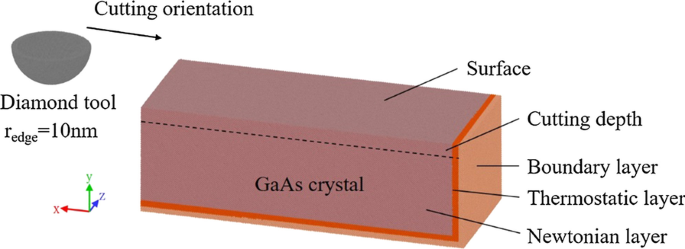
Modelo de simulação MD

O potencial é a base para o cálculo da força e energia entre os átomos e também é uma das configurações mais importantes na simulação MD. No estudo anterior, um sistema de potencial consistindo de três tipos de potencial foi determinado para a simulação do modelo de arsenieto de gálio e ferramenta de diamante [18]. Neste sistema, um potencial de Tersoff-Brenner é usado para descrever a interação entre Ga e As, mostrando um bom efeito de simulação [19]. Um potencial repulsivo exponencial é estabelecido para descrever a interação entre a ferramenta de diamante e a peça de trabalho de arseneto de gálio por meio de um método químico quântico, que está na forma de um potencial de Born-Mayer simplificado [18]. Um potencial Tersoff-ZBL é usado na ferramenta de diamante. O sistema potencial está resumido na Fig. 2.

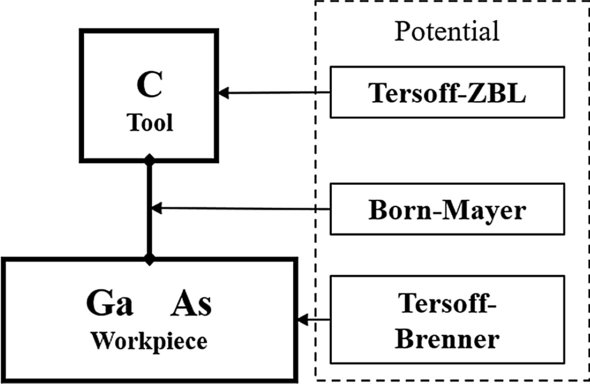
Sistema potencial no modelo

O LAMMPS é utilizado para realizar a simulação MD, enquanto a visualização e análise são via OVITO, incluindo a análise de deslocamento (DXA), cálculo de tensões e análise de coordenação. O relaxamento da peça de trabalho é definido como um conjunto NPT para minimizar a energia do sistema e estabilizar a superfície livre, enquanto o processo de nano corte é definido como um conjunto NVE. O intervalo de tempo para a integração na simulação é 1,0 fs.

Resultados e discussão

Descrição geral

Como é mostrado na Fig. 3, a peça de trabalho de arseneto de gálio é usinada a uma distância de corte de 60 nm com uma velocidade de corte de 400 m / s ao longo da direção [\ (\ overline {1} \) 00] no (010) avião. A peça é colorida com o deslocamento do átomo no y -direção. Observa-se que os átomos na frente da ferramenta fluem para cima, tornando-se aparas por extrusão. Um monte de átomos flui para baixo e forma a superfície usinada. Em ambos os lados da ranhura usinada, os átomos se acumulam com uma altura de 2 nm devido à extrusão e aração da ferramenta. O resultado revela que a deformação e remoção do frágil cristal de arseneto de gálio representa um comportamento dúctil quando a usinagem é em escala nanométrica. Poucos aglomerados de arseneto precipitando na superfície usinada são evidentes no processo de simulação. Este estudo revela a presença de precipitação de arseneto após o recozimento [20]. O potencial de Tersoff-Brenner foi capaz de simular a precipitação de aglomerados de arseneto [19]. No processo de corte, o material da superfície é aquecido com um calor de corte e então recozido, formando aglomerados de arseneto. No entanto, essa precipitação não é uma grande preocupação no processo de nano corte. Portanto, esses átomos ficarão ocultos na análise subsequente.

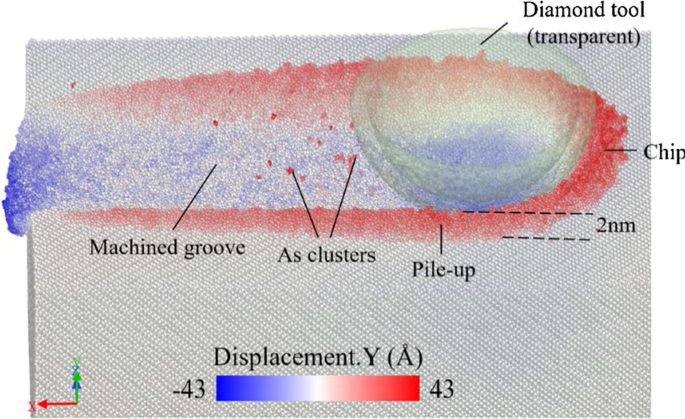
Resultado da simulação de nanocorte colorido com o deslocamento do átomo no y -direção

Compare a curva da força de corte durante o processo de usinagem na Fig. 4. Inicialmente, a força tangencial e a força normal aumentam com o corte da ferramenta no material. A força lateral flutua em torno de 0 porque as forças se cancelam no z -direção. Quando as forças são estabilizadas, a força normal e a força tangencial flutuam em torno de 1700 nN e 700 nN, respectivamente. Verifica-se que a força no y A direção é dominante no processo de corte por causa do grande ângulo de ataque negativo efetivo da ferramenta de diamante, conforme apresentado no modelo. O ângulo de saída negativo traz uma grande tensão de compressão, o que causa uma alta força normal no processo de corte.

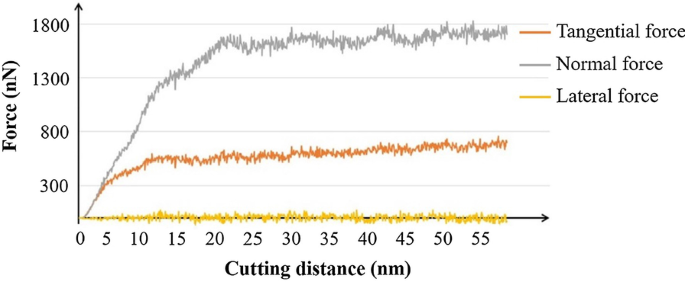
Força de corte no processo de nano corte

Deslocamentos e falhas de empilhamento

A formação de danos subterrâneos é uma parte importante do estudo do mecanismo de nano-corte. É necessário descobrir o mecanismo de formação de danos do arseneto de gálio durante a usinagem para otimizar ainda mais os parâmetros de processamento. Os cristais possuem anisotropia na estrutura atômica, sendo um dos problemas mais sérios no processo de usinagem, o que afetaria o desempenho do processo em diferentes orientações.

A distribuição de deslocamentos na subsuperfície usinada é mostrada na Fig. 5, e o movimento da ferramenta é ao longo de (010) [\ (\ overline {1} \) 00] orientação de corte. Os deslocamentos são observados ao redor do sulco usinado, formando uma camada de deslocamento de cerca de 8 nm. Dois tipos principais de deslocamentos estão presentes na subsuperfície usinada. Os deslocamentos de 1/2 [110] deslizam principalmente nas duas paredes laterais da ranhura usinada, enquanto os deslocamentos de 1/6 [112] se distribuem sob a parte inferior da ranhura. Os deslocamentos 1/2 [110] e 1/6 [112] provaram ser deslocamentos perfeitos (linhas azuis) e deslocamentos parciais (linhas verdes), respectivamente. A formação de deslocamentos significa os movimentos transitivos dos átomos locais, o que implica que a deformação e a remoção estão no estado dúctil. Está provado que o material quebradiço também apresenta um estado dúctil em uma escala suficientemente pequena.

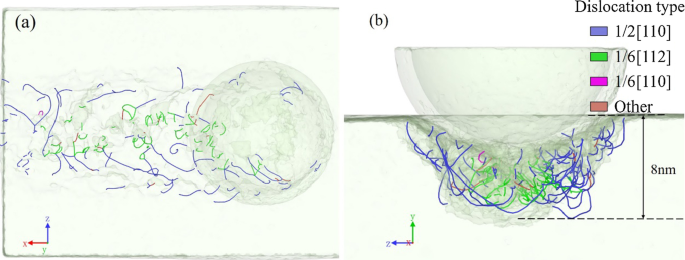
Vistas em perspectiva da distribuição de deslocamento na subsuperfície usinada, em a y -direcção e b x -direção

A tensão de von Mises, que é calculada incluindo os componentes da tensão de cisalhamento, é geralmente usada para determinar a formação do deslocamento. A Figura 6 é a vista em corte transversal do deslocamento e a distribuição de tensões de von Mises. A área de alta tensão está concentrada sob a ferramenta por causa da extrusão. Quando a tensão exercida pela ferramenta excede a resistência ao escoamento do material da peça, o material deslizará ao longo da superfície de deslizamento e o movimento relativo do material de deslizamento causará deslocamentos. Portanto, os deslocamentos nucleados e se estendem para o cristal único por causa da alta tensão na área de usinagem. A energia local será liberada pelo movimento atômico.

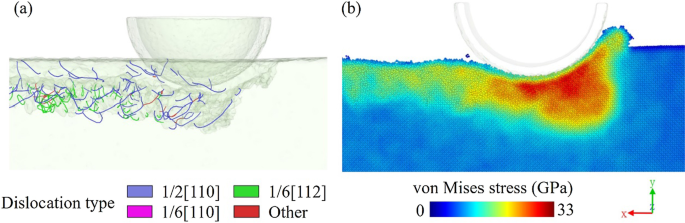
a Distribuição de deslocamento e b Distribuição de tensão de von Mises na subsuperfície do modelo de nano corte

Os deslocamentos nos materiais frágeis e dúcteis são muito diferentes. O arsenieto de gálio é um cristal quebradiço típico, e os deslocamentos estão concentrados perto da superfície usinada. No entanto, os deslocamentos em materiais dúcteis como o cobre irão se estender e deslizar profundamente na peça de trabalho e formar um cluster de deslocamento de alta densidade durante o processo de corte [21], como mostrado na Fig. 7a. Os deslocamentos resultam da deformação dúctil dos materiais. A extensão de aglomerados de deslocamento para materiais dúcteis leva a uma ampla gama de deformações dúcteis e uma tensão difusa. No entanto, a localização de deslocamentos em materiais frágeis como o arseneto de gálio indica que a deformação dúctil ocorre apenas próximo à superfície sem uma liberação completa da tensão. Quando a tensão é concentrada em um valor limite, outros tipos de danos, como transformações de fase ou rachaduras, podem aparecer. Em nosso estudo anterior [18], a formação de rachaduras de arseneto de gálio foi estudada, e foi descoberto que o modo de remoção mudará do modo dúctil com formação de deslocamento para o modo frágil com rachaduras quando a velocidade de corte aumenta. A formação de deslocamento irá liberar a tensão que pode causar o início da fissura e o modo de deformação tenderá a ser dúctil em vez de quebradiço neste caso.

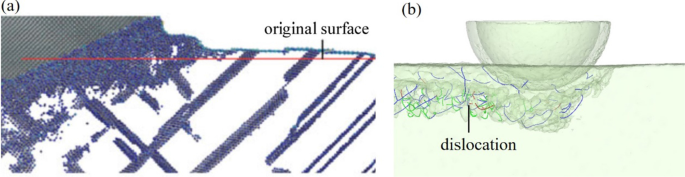
Deslocamento em nano corte de diferentes materiais monocristalinos: a cobre [21] e b arsenieto de gálio

A Figura 8 revela as falhas de empilhamento encontradas na subsuperfície usinada. Os átomos na peça de trabalho são coloridos com base no número de coordenação. Para uma inspeção conveniente, átomos de quatro coordenação com uma estrutura original de zincblende são ocultados. Pode-se observar que existem átomos de três coordenação colocados periodicamente na subsuperfície usinada. Combinado com os deslocamentos parciais encontrados sob o fundo da ranhura, os deslocamentos parciais que são emitidos principalmente dos contornos de grão ou superfícies livres podem causar a formação de falhas de empilhamento ou geminação [22, 23]. As falhas de empilhamento no modelo não são planos atômicos completamente deslocados, mas várias pequenas áreas nos limites do cristal único e da camada amorfa, portanto, os deslocamentos parciais existem nos limites das falhas de empilhamento. Também pode ser inferido que pode haver falhas de empilhamento na subsuperfície usinada real.

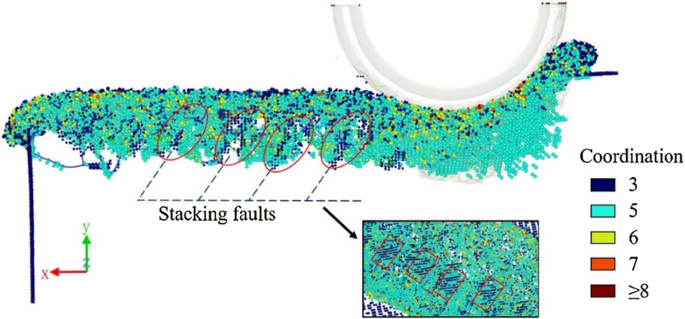
Falhas de empilhamento na subsuperfície usinada

Transformação de fase e amorfização

A estrutura de rede do material pode mudar devido à alta tensão durante o nano corte. Ao estudar o processo de transformação de fase, um melhor entendimento do corte de arseneto de gálio pode ser alcançado, o que é útil para otimizar os parâmetros do processo ou projetar o experimento de pré-tratamento antes do nano corte.

O arsenieto de gálio monocristalino tem uma estrutura de zincblenda sob pressão e temperatura normais. No entanto, a estrutura muda para um GaAs-II de seis coordenadas quando a tensão compressiva atinge 17 GPa [24]. A transformação de fase termina com uma estrutura wurtzite conforme a tensão aumenta além de 60 GPa [25].

A Figura 9a apresenta a mudança estrutural no modelo com uma velocidade de corte de 400 m / s na orientação (010) [\ (\ overline {1} \) 00]. Uma camada da área usinada é observada exibindo uma estrutura amorfa com uma espessura de cerca de 6 nm sem a estrutura característica do cristal.

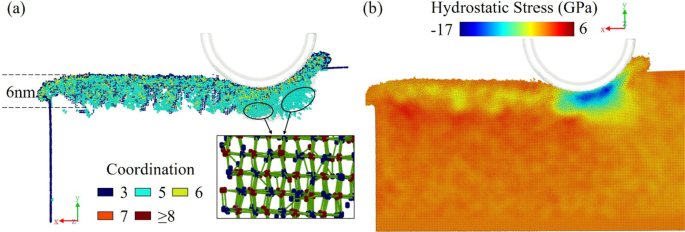
Distribuição de a átomos de alta coordenação e estrutura de cinco coordenação e b distribuição de estresse hidrostático

É óbvio que alguns átomos sob a posição de usinagem se transformam em uma estrutura de cinco coordenação. Semelhante à estrutura bct-5 de formação de cristal de silício com tensão compressiva, esta estrutura de coordenação de cinco é considerada como um intermediário na formação de GaAs-I de seis coordenadas. A tensão hidrostática aumenta e causa a distorção da rede com o corte da ferramenta. No entanto, como é mostrado na distribuição da tensão hidrostática da Fig. 9b, a tensão hidrostática máxima é de 17 GPa, que apenas atinge o valor crítico de transformação de GaAs-I para GaAs-II. A área subsuperficial onde a tensão hidrostática é superior a 17 GPa é muito pequena e a maior parte da área da peça tem uma tensão hidrostática abaixo do limite de transição. Como resultado, é difícil encontrar grandes pedaços de átomos com uma estrutura de seis coordenação e a estrutura de cinco coordenação é uma fase intermediária de GaAs-I a GaAs-II.

A Figura 10 representa as curvas da função de distribuição radial de uma área selecionada no processo de corte, que é a área abaixo da ferramenta de diamante. As curvas de distribuição radial antes, durante e depois do processamento são calculadas. A peça apresenta uma estrutura de zincblenda ordenada no início, cuja curva consiste em picos regulares. Quando a ferramenta de diamante atinge a área selecionada, a função de distribuição radial mostra um estado desordenado em curto e longo alcance. Isso implica na presença de uma forte amorfização com o arranjo desordenado dos átomos na área. No entanto, a curva da subsuperfície usinada implica que a estrutura pode se recuperar e torna-se ordenada no curto alcance e desordenada no longo alcance. Com a liberação da tensão, o material mudará a estrutura para uma com um estado de energia mínimo. Os átomos com uma fase intermediária podem mudar para amorfo ou outro estado. Assim, a curva mostra um estado usinado estável com arsenieto de gálio amorfo. Pode-se descobrir que há um pico lateral em 3,3 Å no processo de usinagem, e o pico desaparece quando a ferramenta sai. Esse fenômeno revela a formação e desaparecimento da fase intermediária, que pode ser considerada como a deformação elástica no processo de corte. Sem a força da ferramenta, parte dos átomos obterá recuperação para a estrutura do zincblende, e os demais mudarão para outra fase estável ou estado amorfo, que representa a deformação dúctil permanente.

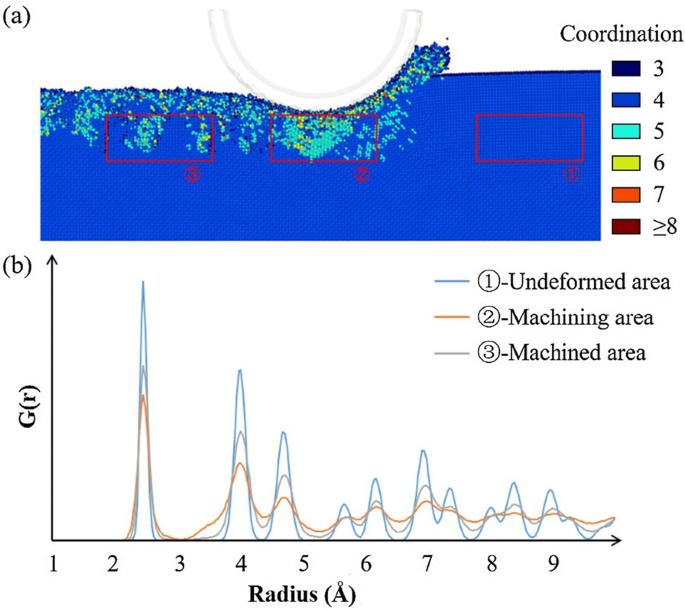
Função de distribuição radial da área selecionada: a áreas selecionadas; b curvas de função de distribuição radial correspondentes

Velocidade de corte e efeitos de orientação na deformação do subsolo

A formação de danos de superfície / subsuperfície é influenciada por muitos fatores e diferentes parâmetros de corte afetarão a formação do deslocamento.

As distribuições de deslocamento com diferentes velocidades de corte são comparadas na Fig. 11a-c. A densidade de deslocamento diminui gradualmente à medida que a velocidade de corte aumenta. A subsuperfície usinada é ricamente fornecida com deslocamentos, especialmente quando a velocidade de corte está abaixo de 200 m / s. Quando o processo de corte está sob uma alta taxa de deformação, não há tempo suficiente para a nucleação e propagação do deslocamento. Como resultado, há menos luxações e a deformação dúctil induzida por luxações também é menos dominante. O material será deformado e desorganizado rapidamente, e o tempo de recuperação também será curto, e átomos amorfos com estrutura não regular serão mais fáceis de formar. Portanto, uma velocidade de corte maior é uma forma de conter a formação de deslocamentos. A Figura 11d-f são as vistas em seção transversal da distribuição de tensões de von Mises nos três modelos correspondentes. Em uma velocidade de corte mais alta, a tensão do material próximo à ferramenta é relativamente maior por causa da grande energia de corte. Comparando os três modelos, o modelo de 800 m / s tem uma maior concentração de tensões na frente da ferramenta, e a subsuperfície usinada apresenta uma região de tensões mais contínua com valores mais altos. Ao contrário, o estresse é liberado devido à formação de deslocamentos nos modelos de baixa velocidade. A deformação dúctil induzida pelos deslocamentos liberará a energia de deformação local e a tensão causada pela flexão e deformação elástica da rede. Portanto, na peça com maior velocidade de corte, o estado de tensões pode ser severo devido à ausência de deslocamentos, facilitando a formação de trincas no processo de corte.

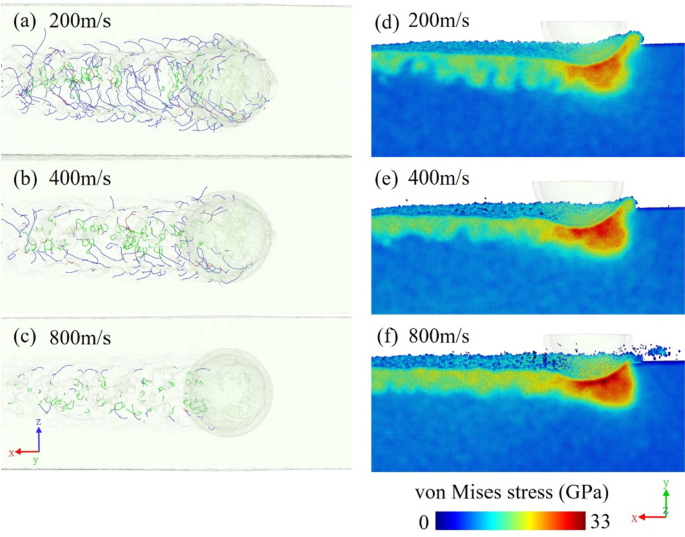
Vistas em perspectiva da distribuição de deslocamento e distribuições de tensão de von Mises em modelos com diferentes velocidades de corte de a , d 200 m / s, b , e 400 m / s e c , f 800 m / s

A anisotropia é um problema sério no processo de nano corte do cristal [26, 27], incluindo o arsenieto de gálio de cristal único. Devido à sua estrutura de cristal único, o cristal de arseneto de gálio apresenta propriedades distintas em diferentes orientações de cristal. Três modelos com diferentes planos e orientações de corte são construídos para estudar a anisotropia. As orientações de corte são (010) [\ (\ overline {1} \) 00], (\ (\ overline {1} \) 10) [\ (\ overline {1} \) \ (\ overline {1} \ ) 0], e \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \). A Figura 12a-f reflete as grandes diferenças que existem entre as distribuições de deslocamento. Conforme afirmado acima, existem dois tipos de deslocamentos no modelo (010) [\ (\ overline {1} \) 00]. Quando a direção de corte está ao longo da direção \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \), a maioria dos deslocamentos estão na parte inferior da ranhura usinada, enquanto alguns deslocamentos agrupados estendem-se à superfície na frente da ferramenta. Poucos deslocamentos são encontrados em ambos os lados da parede lateral na Fig. 12b. Na orientação de corte \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \), deslocamentos semelhantes a árvores que se estendem do meio para ambos os lados são observados , cobrindo a subsuperfície usinada, conforme revelado na Fig. 12c. No entanto, ao contrário do primeiro modelo, existem poucos deslocamentos parciais no \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) e \ ((\ overline {2} 11) modelos \, [\ overline {1} \ overline {1} \ overline {1}] \), e a maioria dos deslocamentos são deslocamentos perfeitos ao longo da orientação [110]. Da mesma forma, as falhas de empilhamento não são encontradas na área usinada de \ (\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) e \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) modelos, correspondendo à ausência de deslocamentos parciais. Isso também prova o efeito da anisotropia no material.

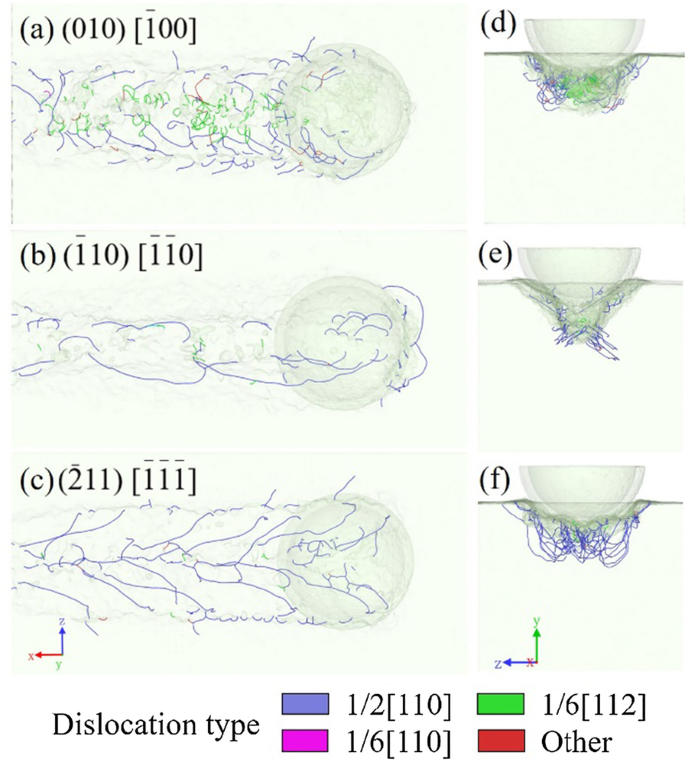
Vistas em perspectiva da distribuição de deslocamento nos modelos com orientações de corte ao longo de a , d \ ((010) \, [\ overline {1} 00] \), b , e \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) e c , f \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \)

A Figura 13a-f compara a distribuição de deslocamento e a distribuição de tensão de von Mises dos três modelos com diferentes orientações de corte. A orientação do cristal tem um efeito óbvio na propagação de tensões. Nos modelos (010) [\ (\ overline {1} \) 00] e \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) , a tensão é concentrada na frente da ferramenta de diamante, mas as direções de extensão são diferentes. No entanto, a área de tensão concentrada do modelo \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) é mais ampla, e a região de alta tensão na frente da ferramenta se estende até a superfície. Por causa da diferença nas orientações do cristal, os componentes de tensão ao longo da direção de deslizamento serão diferentes, resultando em diferentes aparências de deslocamentos. Quando o ângulo da direção da tensão e da superfície de deslizamento são pequenos, é mais provável que o deslizamento apareça e o material se deforme no modo dúctil. Ao contrário, a trinca e a fratura frágil tendem a iniciar quando a razão entre a tensão de tração perpendicular ao plano de clivagem e a tensão de cisalhamento ao longo do plano de deslizamento aumenta.

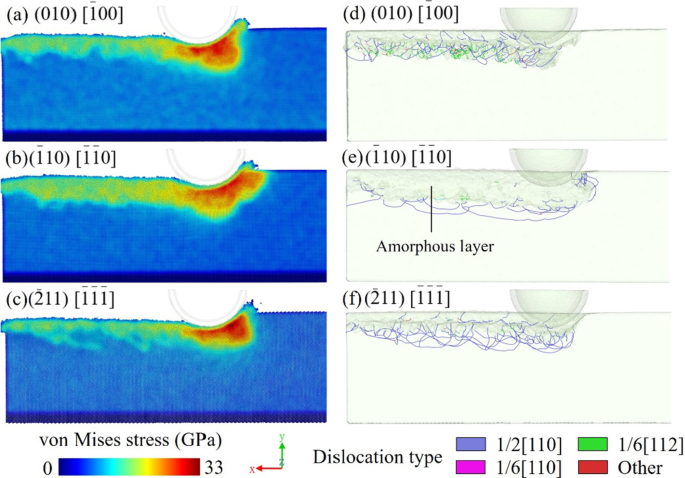
Distribuição de tensão de Von Mises e distribuição de deslocamento nos modelos com orientações de corte ao longo de a , d \ ((010) \, [\ overline {1} 00] \), b , e \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \) e c , f \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \)

Comparando as distribuições de tensão e deslocamento, os modelos com uma densidade de deslocamento mais alta podem ter menor tensão na subsuperfície usinada. A Figura 13e mostra uma camada de dano amorfo mais espessa na subsuperfície do modelo \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \), que corresponde às densas regiões de deslocamento em os outros modelos. Este fenômeno mostra que a anisotropia pode afetar os tipos de danos. No modelo \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \), a tensão concentrada é difícil de ser liberada por causa da menor formação de deslocamento. Como resultado, o arranjo dos átomos é perturbado sob um estado de forte estresse. A faixa de tensão é maior na subsuperfície usinada e a tensão residual é maior. Pelo contrário, o modelo \ ((\ overline {2} 11) \, [\ overline {1} \ overline {1} \ overline {1}] \) tem uma camada de tensão mais fina na subsuperfície usinada devido ao maior densidade de deslocamento. A formação do deslocamento libera parte do estresse durante o processo de corte. No estudo anterior [18], quando o modo de dano dúctil muda de deslocamento para amorfização, a subsuperfície usinada exibe um estado de estresse severo e dano amorfo. As rachaduras de subsuperfície são mais fáceis de formar no limite do cristal amorfo e único. Pode-se inferir que as rachaduras são mais prováveis de ocorrer quando a orientação de corte é ao longo da direção \ ((\ overline {1} 10) \, [\ overline {1} \ overline {1} 0] \). A formação de deslocamento pode reduzir a formação de danos frágeis. Além do mecanismo de clivagem, também é uma razão pela qual a formação de fissuras é afetada pela anisotropia.

No processo de corte, o material próximo à ferramenta de corte recebe alta tensão e severa compressão, o que causará mudanças estruturais no material, como transformação de fase e amorfização. Sob a camada amorfa, o deslizamento ocorrerá em uma área maior e os deslocamentos se formarão no cristal único devido aos efeitos de estresse generalizados. Estas são as principais deformações dúcteis no nano corte de arseneto de gálio. Diferentes condições de corte afetarão o estado de tensão local e a facilidade de formação de deslocamento. Quando os deslocamentos são difíceis de gerar devido à alta velocidade de processamento ou anisotropia, o modo de deformação dúctil tende a ser dominado por amorfo por causa da amorfização causada pelo estresse não liberado. A rachadura também será fácil de se formar nessa situação. Ao contrário, os deslocamentos serão o principal componente da deformação dúctil se as condições forem adequadas ao escorregamento do material.

Conclusão

A simulação MD é usada para estudar o mecanismo de formação de danos no processo de nano corte de cristal de arseneto de gálio. O movimento atômico e a força de corte do processo também são analisados. The dislocation, stacking fault, and phase transformation are mainly studied as the surface/subsurface damages. The conclusions can be summarized as follows:

1.
In the nano-cutting of gallium arsenide, the dislocation and structural transformation are found as the main deformation mechanism in the machined subsurface.
2.
Dislocations and stacking faults are observed in the machined subsurface groove, and the formations of stacking faults and partial dislocations are consistent.
3.
An intermediate phase with five-coordination is found in front of the tool because hydrostatic stress is close to but not higher than the transition threshold (17 GPa). An amorphous layer forms in the machined subsurface.
4.
With increasing cutting speed, the dislocation density decreases because of the high strain rate. Anisotropy has a great effect on the dislocation type and density. Partial dislocations are easier to form in the (010) [\(\overline{1}\)00] model. Moreover, the \((\overline{1}10)\,[\overline{1}\overline{1}0]\) model has a lower dislocation density and a more severe amorphization.

Disponibilidade de dados e materiais

The datasets generated or analysed during the current study are not publicly available due the data also forms part of an ongoing study, but are available from the corresponding author on reasonable request.

Abreviações

MD:: Dinâmica Molecular
GaAs:: Gallium arsenide
FE:: Finite element
FCC:: Face centered cubic
Tersoff-ZBL:: Tersoff-Ziegler–Biersack–Littmark
LAMMPS:: Simulador atômico / molecular maciçamente paralelo em larga escala
OVITO:: Open visualization tool
NPT:: Number-pressure–temperature, isothermal-isobaric ensemble
NVE:: Number-volume-energy, microcanonical ensemble

Au @ Ag Core @ Shell Nanopartículas Sintetizadas com Rumex hymenosepalus como Agente Antimicrobiano Fabricação conformada de um tapete de nanofibra eletrofiado em um coletor de hidrogel em forma de cartilagem de orelha 3D baseado em eletrofiação assistida por hidrogel

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias