Não ligue para as células no mapa de Karnaugh

Até este ponto, consideramos problemas de redução lógica em que as condições de entrada foram completamente especificadas. Ou seja, uma tabela verdade de 3 variáveis ​​ou mapa de Karnaugh tinha 2 ⁿ =2 ³ ou 8 entradas, uma tabela ou mapa completo.

Nem sempre é necessário preencher a tabela de verdade completa para alguns problemas do mundo real. Podemos ter a opção de não preencher a tabela completa.

Por exemplo, ao lidar com números BCD (Binary Coded Decimal) codificados como quatro bits, podemos não nos importar com os códigos acima da faixa BCD de (0, 1, 2… 9). Os códigos binários de 4 bits para os números hexadecimais (Ah, Bh, Ch, Eh, Fh) não são códigos BCD válidos.

Assim, não precisamos preencher esses códigos no final de uma tabela verdade, ou K-map, se não nos importarmos.

Normalmente, não nos importamos em preencher esses códigos, porque eles (1010, 1011, 1100, 1101, 1110, 1111) nunca existirão enquanto estivermos lidando apenas com números codificados em BCD. Esses seis códigos inválidos são não se importa tanto quanto nós estamos preocupados.

Ou seja, não nos importamos com qual saída nosso circuito lógico produz para esses não importa.

Não se preocupe

Não se preocupe com um mapa de Karnaugh, ou tabela de verdade, pode ser 1 s ou 0 s, contanto que não nos importemos com qual é a saída para uma condição de entrada que nunca esperamos ver. Representamos essas células com um asterisco, *, entre os 1 normais se 0 s.

Ao formar grupos de células, trate a célula irrelevante como um 1 ou um 0 , ou ignore o não se importa.

Isso é útil se nos permite formar um grupo maior do que seria possível sem a preocupação. Não há nenhum requisito para agrupar todos ou qualquer um dos não importa.

Use-os em um grupo apenas se isso simplificar a lógica.







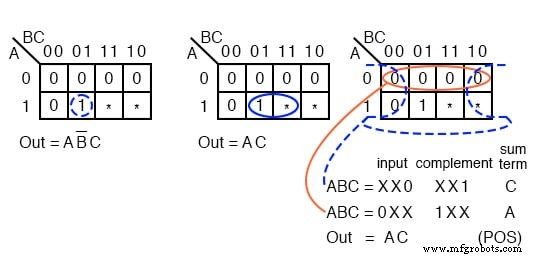
Acima está um exemplo de uma função lógica em que a saída desejada é 1 para entrada ABC =101 no intervalo de 000 a 101 . Não nos importamos qual é a saída para as outras entradas possíveis ( 110, 111) . Mapeie esses dois sem se importar. Mostramos duas soluções.

A solução à direita Out =AB’C é a solução mais complexa, uma vez que não usamos as células não importam. A solução no meio, Out =AC, é menos complexa porque agrupamos uma célula irrelevante com o único 1 para formar um grupo de dois.

A terceira solução, um Produto-das-somas à direita, resulta do agrupamento de não importa com três zeros formando um grupo de quatro 0 s. Este é o mesmo, menos complexo, Out =AC .

Nós ilustramos que as células não se importam podem ser usadas como 1 s ou 0 s, o que for útil.





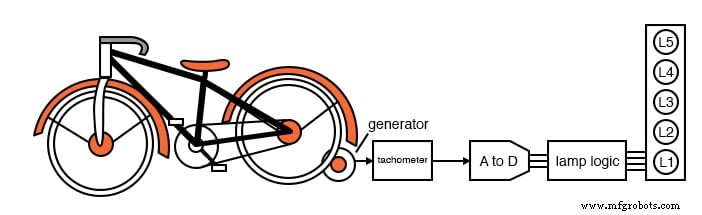
A classe de eletrônica do Lightning State College foi solicitada a construir a lógica da lâmpada para uma exposição de bicicletas ergométricas no museu de ciências local. À medida que o motociclista aumenta a velocidade de pedalada, as lâmpadas acendem em um gráfico de barras.

Nenhuma lâmpada acenderá sem movimento. À medida que a velocidade aumenta, a lâmpada inferior, L1, acende, depois L1 e L2 e, a seguir, L1, L2 e L3, até que todas as lâmpadas acendam na velocidade mais alta. Uma vez que todas as lâmpadas acendam, nenhum aumento adicional na velocidade terá qualquer efeito no visor.

Um pequeno gerador CC acoplado ao pneu da bicicleta emite uma tensão proporcional à velocidade. Ele aciona uma placa de tacômetro que limita a tensão na extremidade superior da velocidade onde todas as lâmpadas se acendem. Nenhum aumento adicional na velocidade pode aumentar a tensão além deste nível.

Isso é crucial porque o conversor downstream de A para D (analógico para digital) emite um código de 3 bits, ABC , 2 ³ ou códigos de 8, mas temos apenas cinco lâmpadas. A é o bit mais significativo, C o bit menos significativo.

A lógica da lâmpada precisa responder aos seis códigos de A a D. Para ABC =000 , nenhum movimento, nenhuma lâmpada acesa. Para os cinco códigos (001 a 101) As lâmpadas L1, L1 e L2, L1 e L2 e L3, até todas as lâmpadas acenderão, conforme a velocidade, a voltagem e o código de A a D (ABC) aumentam.

Não nos importamos com a resposta aos códigos de entrada (110, 111) porque esses códigos nunca sairão de A a D devido à limitação no bloco do tacômetro. Precisamos projetar cinco circuitos lógicos para acionar as cinco lâmpadas.









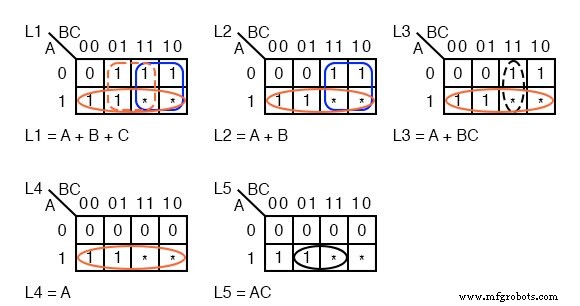
Uma vez que nenhuma das lâmpadas acende para ABC =000 de A a D, insira 0 em todos os K-maps para a célula ABC =000 . Uma vez que não nos importamos com os códigos que nunca serão encontrados (110, 111) , insira asteriscos nessas duas células em todos os cinco mapas K.

A lâmpada L5 acenderá apenas para o código ABC =101 . Insira um 1 nessa célula e cinco 0 s nas células vazias restantes de L5 K-map.

L4 acenderá inicialmente para o código ABC =100 , e permanecerá iluminado para qualquer código superior, ABC =101 , porque todas as lâmpadas abaixo de L5 acenderão quando L5 acender. Digite 1 s em células 100 e 101 do mapa L4 para que acenda para esses códigos. Quatro 0 Preenche as células L4 restantes

L3 acenderá inicialmente para o código ABC =011 . Ele também acenderá sempre que L5 e L4 acenderem. Insira três 1 s nas células 011, 100, 101 para o mapa L3. Preencha três 0 s nas células L3 restantes.

L2 acende para ABC =010 e códigos maiores. Preencher 1 s nas células 010, 011, 100, 101 , e dois 0 s nas células restantes.

O único momento em que L1 não está aceso é para nenhum movimento. Já existe um 0 na célula ABC =000 . Todas as outras cinco células recebem 1 s.

Agrupe o 1 Como mostrado acima, usando não se importa sempre que um grupo maior resulta. O mapa L1 mostra três termos de produto, correspondendo a três grupos de 4 células.

Usamos ambos não se preocupa em dois dos grupos e um não se importa no terceiro grupo. A despreocupação nos permitiu formar grupos de quatro.

De maneira semelhante, os mapas L2 e L4 produzem grupos de 4 células com o auxílio das células don don't care. A redução L4 é notável porque a lâmpada L4 é controlada pelo bit mais significativo do conversor A para D, L5 =A .

Nenhuma porta lógica é necessária para a lâmpada L4. Nos mapas L3 e L5, as células individuais formam grupos de duas com células irrelevantes. Em todos os cinco mapas, a equação booleana reduzida é menos complexa do que sem a preocupação.







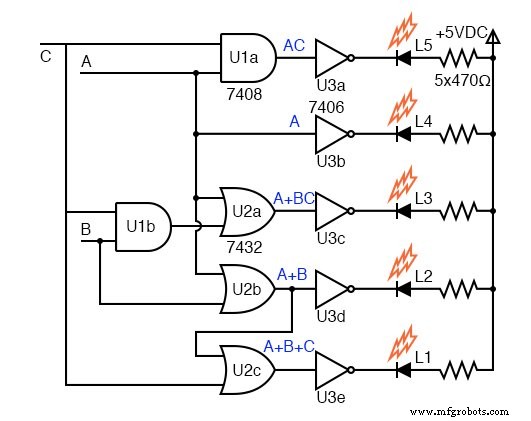
O diagrama do portão para o circuito está acima. As saídas das cinco equações K-map acionam os inversores. Observe que o L1 OU porta não é uma porta de 3 entradas, mas uma porta de 2 entradas com entradas (A + B), C , gerando A + B + C O coletor aberto inversores, 7406 , são desejáveis ​​para acionar LEDs, embora não façam parte do projeto lógico do K-map.

A saída de uma porta de coletor aberto ou inversor é em circuito aberto no coletor interno ao pacote de circuito integrado de modo que toda a corrente do coletor possa fluir através de uma carga externa. Um alto ativo em qualquer um dos inversores puxa a saída para baixo, extraindo corrente através do LED e do resistor limitador de corrente.

Os LEDs provavelmente seriam parte de um relé de estado sólido conduzindo lâmpadas de 120 VAC para uma exposição de museu, não mostrada aqui.



PLANILHAS RELACIONADAS:

• Planilha de circuitos de exibição digital
• Planilha de mapeamento de Karnaugh