Fazendo um diagrama de Venn se parecer com um mapa de Karnaugh

Começando com o círculo A em um universo retangular A ’ na figura (a) abaixo, transformamos um diagrama de Venn em quase um mapa de Karnaugh.







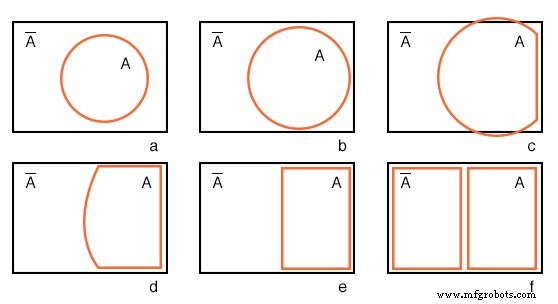
Expandimos o círculo A em (b) e (c), conformar-se ao universo retangular A ’ em (d), e alterar A para um retângulo em (e). Qualquer coisa deixada fora de A é A ’ . Atribuímos um retângulo a A ’ em (f). Além disso, não usamos sombreamento em mapas de Karnaugh. O que temos até agora se assemelha a um mapa de Karnaugh de 1 variável, mas é de pouca utilidade. Precisamos de várias variáveis.







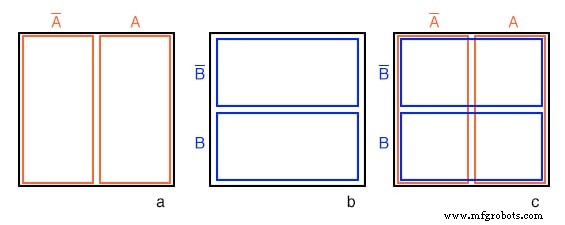
A Figura (a) acima é igual ao diagrama de Venn anterior mostrando A e A ’ acima, exceto que os rótulos A e A ’ estão acima do diagrama em vez de dentro das respectivas regiões. Imagine que passamos por um processo semelhante às figuras (a-f) para obter um “diagrama de Venn quadrado” para B e B ’ como mostramos na figura do meio (b).

Vamos agora sobrepor os diagramas nas Figuras (a) e (b) para obter o resultado em (c), assim como temos feito para os diagramas de Venn. A razão de fazermos isso é para que possamos observar o que pode ser comum a duas regiões sobrepostas — digamos, onde A sobrepõe-se B . A célula inferior direita na figura (c) corresponde a AB onde A sobrepõe-se B .







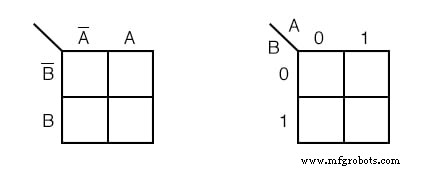
Não perdemos tempo desenhando um mapa de Karnaugh como (c) acima, esboçando uma versão simplificada como acima à esquerda. A coluna de duas células em A ’ é considerado associado a A ’ , e o título A está associado à coluna de células abaixo dele. A linha encabeçada por B ’ está associado às células à direita dele.

De maneira semelhante B está associado às células à direita dele. Por uma questão de simplicidade, não delineamos as várias regiões tão claramente como com os diagramas de Venn.

O mapa de Karnaugh acima à direita é uma forma alternativa usada na maioria dos textos. Os nomes das variáveis ​​são listados ao lado da linha diagonal.

O A acima da diagonal indica que a variável A (e A ’ ) é atribuído às colunas. O 0 é um substituto para A ’ , e o 1 substitutos para A . O B abaixo da diagonal está associada às linhas: 0 para B ’ , e 1 para B

Exemplo:

Marque a célula correspondente à expressão booleana AB no mapa de Karnaugh acima com um 1







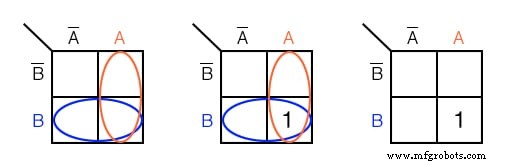
Solução:

Sombreie ou circule a região correspondente a A . Em seguida, sombreie ou delimite a região correspondente a B . A sobreposição das duas regiões é AB . Coloque um 1 nesta célula. Não incluímos necessariamente o A e B regiões como acima à esquerda.

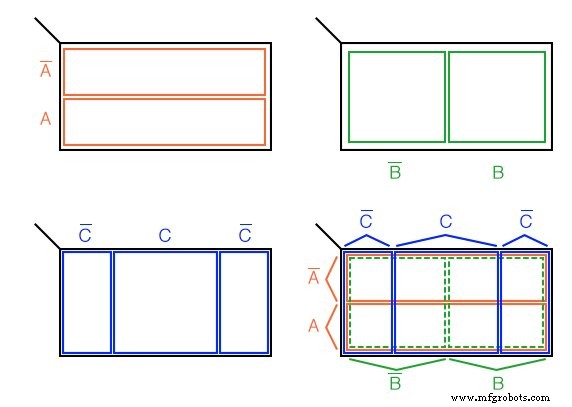
K-map de 3 variáveis ​​

Desenvolvemos um mapa de Karnaugh de 3 variáveis ​​acima, começando com o diagrama de Venn como regiões. O universo (dentro do retângulo preto) é dividido em duas regiões retangulares estreitas e estreitas para A ' e A . As variáveis ​​ B ’ e B divida o universo em duas regiões quadradas. C ocupa uma região quadrada no meio do retângulo, com C ' dividido em dois retângulos verticais em cada lado do C quadrado.

Na figura final, sobrepomos todas as três variáveis, tentando rotular claramente as várias regiões. As regiões são menos óbvias sem a impressão em cores, mais óbvias quando comparadas com as outras três figuras.

Este K-Map de 3 variáveis (Mapa de Karnaugh) tem 2 ³ =8 células , os pequenos quadrados dentro do mapa. Cada célula individual é identificada exclusivamente pelas três variáveis ​​booleanas ( A, B, C ) Por exemplo, ABC ’ seleciona exclusivamente a célula mais inferior direita (*), A’B’C ’ seleciona a célula mais à esquerda (x).







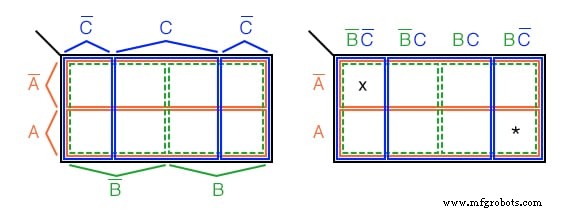
Normalmente não rotulamos o mapa de Karnaugh conforme mostrado acima, à esquerda. Embora esta figura mostre claramente a cobertura do mapa por variáveis ​​booleanas únicas de uma região de 4 células.

Os mapas de Karnaugh são rotulados como a ilustração à direita. Cada célula ainda é identificada exclusivamente por um termo do produto de 3 variáveis , um Booleano AND expressão. Pegue, por exemplo, ABC ’ seguindo o A linha à direita e o BC ’ coluna para baixo, ambas se cruzando na célula inferior direita ABC ’ . Veja (*) a figura acima.







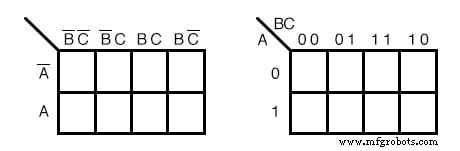
As duas formas diferentes acima de um mapa de Karnaugh de 3 variáveis ​​são equivalentes e é a forma final que assume. A versão à direita é um pouco mais fácil de usar, pois não precisamos escrever tantos cabeçalhos alfabéticos booleanos e barras complementares, apenas 1s e 0s Use a forma do mapa à direita e procure o da esquerda em alguns textos . Os cabeçalhos das colunas à esquerda B’C ’, B’C, BC, BC’ são equivalentes a 00, 01, 11, 10 a direita. Os cabeçalhos de linha A, A ’ são equivalentes a 0, 1 no mapa certo.