Predição e análise eficientes de trapping óptico em nanoescala via elemento finito rasgando e método de interconexão

Resumo

A simulação numérica desempenha um papel importante para a previsão de aprisionamento óptico baseado em pinças nano-ópticas plasmônicas. No entanto, estruturas complicadas e intensificação drástica do campo local dos efeitos plasmônicos trazem grandes desafios aos métodos numéricos tradicionais. Neste artigo, um método de simulação numérica preciso e eficiente baseado em um elemento finito dual primal rasgando e interconectando (FETI-DP) e tensor de tensão de Maxwell é proposto, para calcular a força ótica e o potencial de retenção de nanopartículas. Uma abordagem de esparsificação de baixa classificação é introduzida para melhorar ainda mais o desempenho da simulação FETI-DP. O método proposto pode decompor um problema complexo e de grande escala em problemas simples e de pequena escala, usando divisão de domínio não sobreposta e discretização de malha flexível, que exibe alta eficiência e paralelizabilidade. Resultados numéricos mostram a eficácia do método proposto para a previsão e análise de armadilhas ópticas em nanoescala.

Introdução

Pinças ópticas plasmônicas baseadas em plasmons de superfície (SPs) chamam muita atenção e têm sido amplamente aplicadas para capturar nanopartículas [1,2,3,4,5,6]. SP é um fenômeno de ressonância causado pelo acoplamento da luz incidente com um comprimento de onda específico e elétrons livres na interface dos metais e dielétricos [7]. Os SPs permitem que as pinças ópticas ultrapassem o limite de difração. Além disso, o aumento drástico do campo local dos SPs pode reduzir a demanda de intensidade da luz incidente [7, 8]. No entanto, os SPs estão intimamente relacionados ao material e às dimensões dos objetos, bem como ao comprimento de onda da luz incidente, o que requer um grande número de experimentos para determinar os parâmetros ideais das pinças ópticas SP na prática. Com base nisso, o método de simulação desempenha um papel cada vez mais importante como meio auxiliar para o projeto e otimização de pinças ópticas SP [9]. Nessas simulações, o cálculo da força óptica é necessário para prever um aprisionamento estável. Para objetos regulares, como esferas, a força óptica pode ser derivada analiticamente da teoria de Lorenz-Mie generalizada [10, 11]. No entanto, para objetos com configurações complicadas, os métodos numéricos que resolvem as equações de Maxwell que regem rigorosamente são necessários para modelar os campos eletromagnéticos e a força óptica e potencial subsequentes.

Esses métodos numéricos podem ser categorizados principalmente em métodos de equações diferenciais (DEMs) e métodos de equações integrais (IEMs) [12,13,14,15]. Em comparação com os IEMs, os métodos de equação diferencial (DEMs) mostram habilidades superiores para lidar com geometrias e componentes complicados. DEMs também têm a vantagem de um cálculo direto da distribuição de campo próximo, que desempenha um papel importante na análise de SPs. Como um DEM representativo, o método de domínio de tempo de diferença finita (FDTD) é implementado no domínio do tempo, que pode facilmente obter informações de banda larga e respostas transitórias [16, 17]. No entanto, o FDTD exige um modelo dispersivo preciso para descrever as propriedades do material dependente da frequência em SPs, enquanto a precisão da solução FDTD depende muito da precisão de aproximação deste modelo dispersivo [18]. Além disso, o FDTD depende de malhas estruturadas, que muitas vezes levam a erros de escada para superfícies curvas. Como outro DEM representativo, o método dos elementos finitos (FEM) tem sido amplamente adotado, uma vez que pode facilmente manipular o material dispersivo no domínio da frequência e eliminar o erro de escada por malha não estruturada [19,20,21,22]. Comparado com o FDTD, o FEM pode adotar diretamente parâmetros de material medidos sem qualquer modelo dispersivo aproximado. No entanto, aprimoramentos drásticos de campo local nos SPs exigem malhas finas na discretização do FEM. Além disso, objetos com grandes dimensões e objetos múltiplos aumentarão dramaticamente o número de incógnitas. Esses fatores causarão sistemas matriciais mal condicionados e enormes consumos computacionais, que trazem grandes desafios ao FEM tradicional para a análise de trapping óptico aprimorado por SP.

Neste artigo, um método eficiente de rasgo e interconexão de elemento finito primal dual (FETI-DP) é apresentado para simular o aprisionamento óptico em nanoescala. O FETI-DP adota um esquema de decomposição de domínio não sobreposto, que divide um problema complexo original de grande escala em uma série de problemas simples de pequena escala para superá-los. Ele impõe uma condição de transmissão nas interfaces de subdomínio para garantir a continuidade do campo e introduz uma variável dupla para reduzir o problema tridimensional original (3D) a ser um problema bidimensional (2D) pelo multiplicador de Lagrange. Variáveis primárias nos cantos do subdomínio são extraídas para acelerar a taxa de convergência da solução iterativa do problema dual [23,24,25,26]. Uma abordagem de esparsificação de baixa classificação é desenvolvida para melhorar o desempenho do FETI-DP. Ele usa algoritmos de dados esparsos para melhorar a eficiência para resolver os problemas de subdomínio e o problema dual [27, 28]. O método proposto fornece subdomínios totalmente desacoplados, que permitem a simulação paralela de força óptica para o aprisionamento de nanopartículas. O tensor de tensão de Maxwell (MST) que revela a relação entre o campo eletromagnético e o momento mecânico é adotado para avaliar a força óptica [29]. Com base na força óptica obtida, o potencial óptico pode ainda ser calculado para a análise de um aprisionamento estável. Comparado com os IEMs, o método proposto é mais poderoso para lidar com materiais compostos e resolver o campo próximo para o trapping óptico baseado em SP. Comparado com o FDTD, o método proposto pode manipular com precisão o material de metal dispersivo nos sistemas de captura óptica baseados em SP e eliminar o erro de escada para os objetos com limite de curva. Comparado com o FEM, o método proposto é adequado para computação em larga escala de trapping óptico. Diversos exemplos são analisados e os resultados numéricos demonstram a precisão e eficiência do método proposto para a previsão e análise de armadilhas ópticas em nanoescala.

Métodos

Formulações FETI-DP

Para a implementação FETI-DP, o domínio computacional original Ω é primeiro dividido em uma série de subdomínios não sobrepostos Ω ⁱ ( eu =1, 2, 3 ⋯, N _s ), conforme mostrado na Fig. 1. Em cada subdomínio Ω ⁱ , um sistema de elementos finitos de subdomínio pode ser derivado da equação de onda vetorial como
$$ \ nabla \ times {\ mu} _r ^ {- 1} \ nabla \ times {\ mathbf {E}} ^ i- {k} _0 ^ 2 {\ varepsilon} _r {\ mathbf {E}} ^ i ={jk} _0 {\ eta} _0 {\ mathbf {J}} _ {\ mathrm {imp}} ^ i \ kern1.08em \ mathrm {in} \ kern0.24em {\ Omega} ^ i $$ (1 ) $$ \ hat {n} \ times \ nabla \ times {\ mathbf {E}} ^ i + {jk} _0 \ hat {n} \ times \ left (\ hat {n} \ times {\ mathbf {E} } ^ i \ right) =0 \ kern0.96em \ mathrm {on} \ kern0.24em {\ Gamma} _ {\ mathrm {ABC}} ^ i $$ (2)

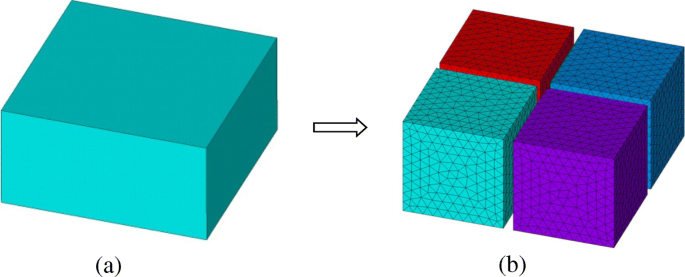
Um esquema de divisão de domínio com subdomínios não sobrepostos no método FETI-DP. a Domínio original. b Subdomínios divididos e malhas discretizadas

onde E ⁱ denota o campo elétrico desconhecido a ser resolvido em \ ({\ Omega} ^ i \), k ₀ e η ₀ são o número de onda do espaço livre e a impedância intrínseca, respectivamente, e \ ({\ mathbf {J}} _ i ^ {\ mathrm {imp}} \) é a corrente impressa. \ ({\ Gamma} _ {\ mathrm {ABC}} ^ i \) significa a condição de contorno absorvente (ABC) para truncar a região aberta infinita. Deve-se notar que k ₀ deve ser substituída pela impedância de onda no meio se o meio circundante não for de espaço livre, o que é comum para o aprisionamento óptico. Na interface do subdomínio Γ ⁱ , uma condição de contorno assumida é necessária para gerar um problema de valor de contorno completo em Ω ⁱ . Aqui, uma condição de transmissão do tipo Robin com uma variável auxiliar desconhecida Λ _i é imposto como
$$ {\ hat {n}} ^ i \ times \ left ({\ mu} _r ^ {- 1} \ nabla \ times {\ mathbf {E}} ^ i \ right) + {\ alpha} ^ i { \ hat {n}} ^ i \ times \ left ({\ hat {n}} ^ i \ times {\ mathbf {E}} ^ i \ right) ={\ boldsymbol {\ Lambda}} ^ i \ kern1. 2em \ mathrm {on} \ kern0.36em {\ Gamma} ^ i $$ (3)
onde \ ({\ hat {n}} ^ i \) denota o vetor de saída normal da unidade na interface do subdomínio Γ ⁱ , e α ⁱ é um parâmetro complexo que geralmente pode ser escolhido como jk ₀ . Todos os subdomínios são então discretizados por elementos tetraédricos. Em cada elemento, expandimos E com funções de base vetorial N e coeficiente de campo elétrico desconhecido E Como
$$ \ mathbf {E} =\ sum \ limits_ {p =1} ^ s {E} _p {\ mathbf {N}} _ p $$ (4)
onde s denota o número de funções de base do vetor em cada elemento tetraédrico. s é escolhido como 6 para a função de base de ordem baixa tradicional com base na aresta, enquanto é maior para a função de base de vetor de ordem alta, uma vez que são introduzidas funções de base adicionais com base na face ou no volume.

Aplicando o método de Galerkin, a equação da matriz FEM em Ω ⁱ sobre o coeficiente de campo elétrico desconhecido E ⁱ pode ser obtido como
$$ \ left (\ begin {array} {cc} {\ mathbf {K}} _ {rr} ^ i &{\ mathbf {K}} _ {rc} ^ i \\ {} {\ mathbf {K}} _ {cr} ^ i &{\ mathbf {K}} _ {cc} ^ i \ end {array} \ right) \ left (\ begin {array} {l} {E} _r ^ i \\ {} {E } _c ^ i \ end {array} \ right) =\ left (\ begin {array} {l} {f} _r ^ i - {\ mathbf {B}} _ r ^ {i ^ T} {\ lambda} ^ i \\ {} {f} _c ^ i \ end {array} \ right) $$ (5)
onde as notações subscritas c e r distinguir os graus de liberdade de canto (DOFs) e os DOFs restantes, que extrai os DOFs de canto como uma variável primária para construir o esquema dual-primal (DP). Aqui, K é a matriz do sistema FEM e f é o vetor de excitação. B é uma matriz booleana que extrai os DOFs da interface de um subdomínio. λ é uma variável dupla gerada a partir da expansão de Λ _i , que também é chamado de multiplicador de Lagrange.

Em seguida, os subdomínios adjacentes podem ser interconectados reforçando o campo elétrico tangencial e a continuidade do campo magnético nas interfaces. Montamos todas as interfaces de subdomínio e eliminamos todas as incógnitas internas do subdomínio E ⁱ . Uma equação de interface global reduzida sobre a variável dupla λ pode ser obtido como
$$ \ left [{\ tilde {\ mathbf {K}}} _ {rr} + {\ tilde {\ mathbf {K}}} _ {rc} {\ tilde {\ mathbf {K}}} _ {cc } ^ {- 1} {\ tilde {\ mathbf {K}}} _ {cr} \ right] \ lambda ={\ tilde {f}} _ r - {\ tilde {\ mathbf {K}}} _ {rc } {\ tilde {\ mathbf {K}}} _ {cc} ^ {- 1} {\ tilde {f}} _ c $$ (6)
A equação (6) pode ser resolvida por métodos iterativos, como o método residual mínimo generalizado (GMRES). \ ({\ tilde {\ mathbf {K}}} _ {cc} \) é o sistema de canto global, que pode acelerar a convergência iterativa no espaço primal. O pré-condicionador adequado pode ser empregado para melhorar a taxa de convergência iterativa, como o inverso aproximado e a decomposição LU incompleta. Uma vez que a variável dupla λ for resolvido, o campo elétrico dentro de cada subdomínio pode ser avaliado de forma independente por (5). Para a construção da matriz global \ ({\ tilde {\ mathbf {K}}} _ {rr} \), é necessário construir a função de Green numérica do subdomínio \ ({\ mathbf {Z}} _ {rr} ^ i \) com uma forma de
$$ {\ mathbf {Z}} _ {rr} ^ i ={\ mathbf {B}} _ r ^ i {\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} {{\ mathbf {B}} _ r ^ i} ^ T $$ (7)
onde o inverso da matriz FEM do subdomínio \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) está incluído. Além disso, para matrizes \ ({\ tilde {\ mathbf {K}}} _ {rc} \), \ ({\ tilde {\ mathbf {K}}} _ {cr} \), e \ ({\ tilde {\ mathbf {K}}} _ {cc} \) e vetores \ ({\ tilde {f}} _ r \) e \ ({\ tilde {f}} _ c \), o \ ({\ left ({ \ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) deve ser calculado. As construções de \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) no estágio de pré-processamento, bem como seus produtos de vetor de matriz (MVPs) em estágios de solução iterativa são computacionalmente caros. Embora \ ({\ mathbf {K}} _ {rr} ^ i \) seja esparso, \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \ ) são densos, o que significa altos custos computacionais. A seguir, um método de esparsificação de baixa classificação é introduzido para acelerar o cálculo de \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \). Uma vez que algumas submatrizes no sistema de interface global podem ser representadas na forma de matriz de classificação baixa, seu cálculo pode ser realizado com algoritmo de classificação inferior, o que melhora o desempenho do FETI-DP. Pode-se ver que o FETI-DP fornece operações de subdomínio independentes, de modo que pode explorar a computação paralela para melhorar a eficiência. Para um esquema paralelo eficiente, um princípio de divisão de domínio é tornar o número de DOFs em cada subdomínio o mais balanceado possível. Portanto, o tamanho dos subdomínios deve estar relacionado à densidade de discretização da malha. Normalmente, pequenos subdomínios são adotados em áreas de malha fina, enquanto subdomínios grandes são adotados em áreas de malha grosseira.

Esparsificação de baixa classificação

Uma abordagem de esparsificação de baixa classificação é proposta para fornecer uma maneira esparsa de dados para melhorar a eficiência do FETI-DP. Aqui, dados esparsos significa que essas matrizes não são realmente esparsas, mas são esparsas no sentido de que certos sub-blocos delas podem ser representados por formas de matriz de decomposição de baixa classificação como
$$ \ mathbf {M} ={\ mathbf {XY}} ^ {\ mathrm {T}} \ kern0.72em \ left (\ mathbf {M} \ in {\ mathrm {\ mathbb {C}}} ^ { m \ times n}, \ mathbf {X} \ in {\ mathrm {\ mathbb {C}}} ^ {m \ times k}, \ mathbf {Y} \ in {\ mathrm {\ mathbb {C}}} ^ {n \ vezes k} \ direita) $$ (8)
onde X e Y estão em formas de matriz completa, e a classificação k é muito menor que m e n . A matriz \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) pode ser representada por formas de matriz esparsas de dados, uma vez que possui a propriedade de matriz de uma integral operador. Portanto, desde que \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} ^ {- 1} \) possua propriedade de baixa classificação em determinado subdomínio, pode ser eficientemente calculado e armazenado em formulários de dados esparsos com a abordagem de esparsificação de baixa classificação, que acelera os MVPs na solução iterativa.

Os processos da abordagem de esparsificação de baixa classificação podem ser divididos nas seguintes etapas:(1) construir uma árvore de cluster subdividindo o conjunto de funções de base em cada subdomínio, (2) construir uma árvore de cluster de bloco pela interação de duas árvores de cluster, ( 3) gerar uma forma de dados esparsos de \ ({\ mathbf {K}} _ {rr} ^ i \) por uma condição de admissibilidade, (4) realizar algoritmos formatados de baixa classificação para obter a representação de dados esparsos de \ ( {\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \), e (5) insira a solução de sistemas FETI-DP por algoritmo de dados esparsos. Um pré-condicionador adequado pode ser empregado para acelerar a solução. Deve-se notar que a fatoração LU de dados esparsos \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ={\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS} } \) é adotado para substituir a inversão da matriz \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \). Uma técnica de dissecção aninhada é empregada para melhorar ainda mais a eficiência da esparsificação de baixa classificação. A dissecção aninhada usa separadores para produzir grandes sub-blocos de zero fora da diagonal, que manterão zero durante a fatoração LU para que possam reduzir significativamente os preenchimentos.

Para gerar \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \), primeiro construímos uma árvore de cluster T _eu por subdivisão recursiva do conjunto de funções de base baseadas na borda do subdomínio I ={1,2, …… N } usando a caixa delimitadora. Com a dissecção aninhada, um cluster t dentro da caixa delimitadora correspondente é dividido em três sucessores { s ₁ , s _sep , s ₂ }, onde s ₁ e s ₂ são os conjuntos de índices das duas caixas delimitadoras desconectadas e s _sep é o conjunto de índices do separador. A Figura 2a mostra um exemplo simples desse processo. Então, uma árvore de cluster de bloco T _{eu × I} pode ser construído interagindo com duas árvores de cluster T _eu , como mostrado na Fig. 2b, que pode ser escolhido como a árvore de agrupamento do conjunto de funções de base com base na borda original e do conjunto de funções de base de teste no método de Galerkin. Em seguida, precisamos introduzir uma condição de admissibilidade com base na dissecção aninhada para distinguir blocos completos, blocos de decomposição de baixa classificação e blocos zero fora da diagonal em T _{eu × I} [23]. Assim, \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) pode ser produzido preenchendo os blocos correspondentes com as entradas diferentes de zero de \ ({\ mathbf {K}} _ {rr} ^ i \). Finalmente, a fatoração LU de dados esparsos de \ ({\ left ({\ mathbf {K}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ={\ left ({\ mathbf {L }} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \ ) pode ser calculado recursivamente a partir de
$$ {\ mathbf {K}} _ {rr} ^ i =\ left [\ begin {array} {ccc} {\ mathbf {K}} _ {11} &&{\ mathbf {K}} _ {13 } \\ {} &{\ mathbf {K}} _ {22} &{\ mathbf {K}} _ {23} \\ {} {\ mathbf {K}} _ {31} &{\ mathbf {K }} _ {32} &{\ mathbf {K}} _ {33} \ end {array} \ right] =\ left [\ begin {array} {ccc} {\ mathbf {L}} _ {11} &&\\ {} &{\ mathbf {L}} _ {22} &\\ {} {\ mathbf {L}} _ {31} &{\ mathbf {L}} _ {32} &{\ mathbf { L}} _ {33} \ end {array} \ right] \ left [\ begin {array} {ccc} {\ mathbf {U}} _ {11} &&{\ mathbf {U}} _ {13} \\ {} &{\ mathbf {U}} _ {22} &{\ mathbf {U}} _ {23} \\ {} &&{\ mathbf {U}} _ {33} \ end {array} \ right] $$ (9)

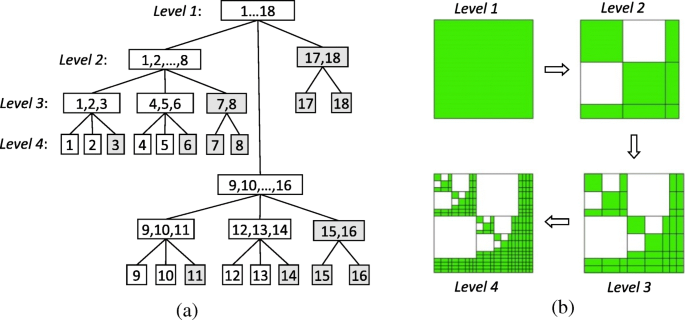
Construções de uma árvore de cluster e uma árvore de cluster de bloco de 4 níveis com base na dissecção aninhada. a Construção de uma árvore de cluster por subdivisão recursiva do conjunto de funções de base com base na borda I ={1,2,… 18}. b Construção de uma árvore de agrupamento de blocos onde branco blocos são matrizes zero e verdes os blocos podem ser matrizes completas ou matrizes de decomposição de baixa classificação

onde a aritmética de matriz completa convencional é substituída por suas contrapartes com dados esparsos [28]. Um erro de truncamento adaptativo ε _t é empregado para controlar a precisão das aproximações de classificação inferior. Os fatores LU obtidos \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) e \ ({\ left ({\ mathbf {U} } _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \) são armazenados e usados para construir \ ({\ mathbf {Z}} _ {rr} ^ i \) por
$$ {\ mathbf {Z}} _ {rr} ^ i ={\ mathbf {B}} _ r ^ i {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} {\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} {\ mathbf {B} } _r ^ i $$ (10)
onde \ ({\ mathbf {B}} _ r ^ i {\ left ({\ mathbf {U}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} \) e \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} ^ {- 1} {\ mathbf {B}} _ r ^ i \) pode ser calculado pelo solucionador triangular superior e inferior de dados esparsos. O \ ({\ left ({\ mathbf {L}} _ {rr} ^ i \ right)} _ {\ mathrm {DS}} \), \ ({\ left ({\ mathbf {U}} _ { rr} ^ i \ right)} _ {\ mathrm {DS}} \), e \ ({\ mathbf {Z}} _ {rr} ^ i \) insira o cálculo FETI-DP com dados esparsos para frente e para trás substituições (FBSs) e MVPs com dados esparsos.

Força óptica e potencial

De acordo com a teoria eletrodinâmica, a força óptica pode ser avaliada pelo tensor de tensão de Maxwell (MST) que revela a relação entre o campo eletromagnético e o momento mecânico [29]. Uma vez que a distribuição do campo eletromagnético em torno do objeto é obtida, a força óptica pode ser calculada integrando o MST sobre uma superfície fechada em torno do objeto. Com base na distribuição do campo elétrico obtido, o MST em quaisquer coordenadas pode ser construído por
$$ \ overleftrightarrow {\ mathbf {T}} =\ frac {1} {2} \ operatorname {Re} \ left [\ varepsilon {\ mathbf {EE}} ^ {\ ast} + \ mu {\ mathbf {HH }} ^ {\ ast} - \ frac {1} {2} \ left (\ varepsilon {\ left | \ mathbf {E} \ right |} ^ 2 + \ mu {\ left | \ mathbf {H} \ right |} ^ 2 \ right) \ overleftrightarrow {\ mathbf {I}} \ right] $$ (11)
onde o asterisco sobrescrito denota o conjugado de campo elétrico ou campo magnético, ε são μ são a permissividade e a permeabilidade, e \ (\ overleftrightarrow {\ mathbf {I}} \) é uma matriz de identidade 3 × 3. Pelo produto externo dos vetores, a forma tensorial de \ (\ overleftrightarrow {\ mathbf {T}} \) pode ser escrita como
$$ \ overleftrightarrow {\ mathrm {T}} =\ left [\ begin {array} {lll} {T} _ {xx} &{T} _ {xy} &{T} _ {xz} \\ {} {T} _ {yx} &{T} _ {yy} &{T} _ {yz} \\ {} {T} _ {zx} &{T} _ {zy} &{T} _ {zz} \ end {array} \ right] =\ left [\ begin {array} {ccc} \ varepsilon {E} _x {E} _x ^ {\ ast} + \ mu {H} _x {H} _x ^ {\ ast } - \ frac {\ varepsilon {\ left | \ mathbf {E} \ right |} ^ 2 + \ mu {\ left | \ mathbf {H} \ right |} ^ 2} {2} &\ varepsilon {E} _x {E} _y ^ {\ ast} + \ mu {H} _x {H} _y ^ {\ ast} &\ varepsilon {E} _x {E} _z ^ {\ ast} + \ mu {H} _x { H} _z ^ {\ ast} \\ {} \ varepsilon {E} _y {E} _x ^ {\ ast} + \ mu {H} _y {H} _x ^ {\ ast} &\ varejpsilon {E} _y {E} _y ^ {\ ast} + \ mu {H} _y {H} _y ^ {\ ast} - \ frac {\ varepsilon {\ left | \ mathbf {E} \ right |} ^ 2 + \ mu { \ left | \ mathbf {H} \ right |} ^ 2} {2} &\ varepsilon {E} _y {E} _z ^ {\ ast} + \ mu {H} _y {H} _z ^ {\ ast} \\ {} \ varepsilon {E} _z {E} _x ^ {\ ast} + \ mu {H} _z {H} _x ^ {\ ast} &\ varepsilon {E} _z {E} _y ^ {\ ast } + \ mu {H} _z {H} _y ^ {\ ast} &\ varepsilon {E} _z {E} _z ^ {\ ast} + \ mu {H} _z {H} _z ^ {\ ast} - \ frac {\ varepsilon {\ left | \ mathbf {E} \ right |} ^ 2 + \ mu {\ left | \ mathbf {H} \ right |} ^ 2} {2} \ end {array} \ right] $$ (12)
onde o subscrito x , y , z denota os componentes em três direções. De acordo com a expansão de E descrito em (4), as entradas de MST T _mn ( m , n = x , y , z ) podem ser convertidos em formas expandidas no cálculo FETI-DP como
$$ {\ displaystyle \ begin {array} {l} {T} _ {mn} =\ sum \ limits_ {p, q =1} ^ s {E} _p {E} _q \ left \ {\ varejpsilon {\ esquerda ({\ mathbf {N}} _ p \ direita)} _ m {\ esquerda ({\ mathbf {N}} _ q ^ {\ ast} \ direita)} _ n- \ frac {1} {\ omega ^ 2 \ mu } {\ left (\ nabla \ times {\ mathbf {N}} _ p \ right)} _ m {\ left (\ nabla \ times {\ mathbf {N}} _ q ^ {\ ast} \ right)} _ n \ right . \\ {} \ kern1.75em \ left .- \ frac {1} {2} \ left [\ varepsilon \ left ({\ mathbf {N}} _ p \ right) \ left ({\ mathbf {N}} _q ^ {\ ast} \ right) - \ frac {1} {\ omega ^ 2 \ mu} \ left (\ nabla \ times {\ mathbf {N}} _ p \ right) \ left (\ nabla \ times {\ mathbf {N}} _ q ^ {\ ast} \ right) \ right] \ right \} \ kern1.75em \ mathrm {if} \ m =n. \ end {array}} $$ (13) $$ {T } _ {mn} =\ sum \ limits_ {p, q =1} ^ s {E} _p {E} _q \ left \ {\ varepsilon {\ left ({\ mathbf {N}} _ p \ right)} _ m {\ left ({\ mathbf {N}} _ q ^ {\ ast} \ right)} _ n- \ frac {1} {\ omega ^ 2 \ mu} {\ left (\ nabla \ times {\ mathbf {N} } _p \ right)} _ m {\ left (\ nabla \ times {\ mathbf {N}} _ q ^ {\ ast} \ right)} _ n \ right \} \ kern1.25em \ mathrm {if} \ m \ ne n $$ (14)
onde ω é a frequência angular; N e s foram descritos na Eq. (4).

Finalmente, a força óptica exercida sobre o objeto pode ser calculada integrando o MST sobre qualquer superfície fechada que o rodeia por
$$ \ mathbf {F} ={\ oint} _S \ left (\ overleftrightarrow {\ mathbf {T}} \ cdot \ hat {n} \ right) \ dS. $$ (15)
Observe que o cálculo da força óptica também pode ser implementado em paralelo, uma vez que a integral do MST é atribuída aos subdomínios correspondentes. Para um aprisionamento óptico estável, uma das principais condições é que a força do gradiente deve ser maior do que a força de espalhamento. Em outras palavras, a direção da força total deve ser idêntica à da força gradiente, que sempre aponta para a posição onde a intensidade do campo elétrico é mais forte.

O potencial óptico é outro parâmetro atraente que revela a estabilidade do aprisionamento óptico. Com base na força óptica obtida, a profundidade do potencial óptico U na posição r ₀ pode ser calculado por
$$ \ mathbf {U} \ left ({r} _0 \ right) =- {\ int} _ {\ infty} ^ {r_0} \ mathbf {F} \ left (\ mathbf {r} \ right) \ cdot \ mathbf {r}, $$ (16)
onde o subscrito ∞ denota infinito definido como o ponto de referência com potencial zero. O valor de U pode ser representado por k _B T, onde k _B denota a constante de Boltzmann de 1,3806488 × 10 ⁻²³ J / K e T são a temperatura ambiente. Geralmente, a partícula pode superar o movimento browniano em solução e ficar presa de forma estável quando U > 1 k _B T está satisfeito. Caso contrário, a partícula não pode ser presa de forma estável. Uma vez que a força óptica total inclui o componente de força de gradiente conservativo e o componente de força de espalhamento não conservativo, a força óptica total F de (15) é não conservador [30, 31]. No entanto, desde que o movimento da nanopartícula seja restrito a uma dimensão, isso produz uma definição inequívoca de um potencial óptico de (16), embora a força óptica total seja não conservativa.

Resultados e discussão

Três exemplos são apresentados para demonstrar a eficácia do método proposto. Uma vez que metais nobres são comumente usados para excitar o plasmon de superfície, selecionamos materiais representativos de ouro e prata para as análises. O primeiro exemplo calcula a força óptica da nanopartícula de prata para verificar a precisão do método proposto. O segundo e o terceiro exemplos simulam e discutem o aprisionamento óptico de nanopartículas de ouro. Para todos os exemplos, o domínio infinito é truncado com ABC e as distâncias entre o ABC e os objetos são definidas como um comprimento de onda, o que é suficiente para atingir uma precisão aceitável. Todos os cálculos são executados em uma estação de trabalho Dell equipada com processadores Intel Xeon de 3,6 GHz.

Nanocápsula de prata

Um objeto de nanocápsula de prata é considerado pela primeira vez para testar a precisão e eficiência do método FETI-DP proposto na previsão de força óptica. A Figura 3 aeb apresenta sua configuração e dimensões. Os parâmetros constitutivos da prata são todos os valores medidos retirados de [32]. Para implementar o esquema FETI-DP, todo o domínio de análise é primeiro dividido em 24 subdomínios. Malhas mais densas são necessárias perto da superfície do metal para modelar o efeito de intensificação do campo plasmônico local. Elementos tetraédricos são adotados para a discretização, o que leva a um total de 6,9 × 10 ⁵ desconhecidos, incluindo 4,1 × 10 ⁴ desconhecidos duais e 313 desconhecidos de canto. A luz incidente ilumina ao longo da direção de + z , enquanto a direção da polarização do campo elétrico é - x .

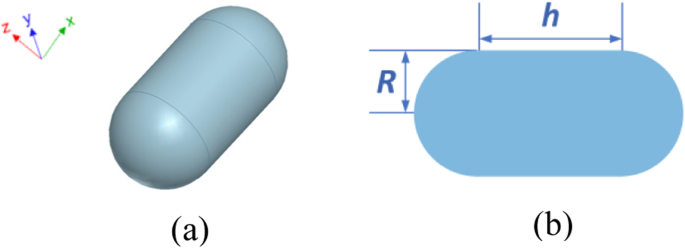
Configuração de uma estrutura de nanocápsula de prata. a Visualização 3D. b Vista frontal e dimensões, onde R =30 nm e h =60 nm

Primeiro, mudamos o comprimento de onda da luz incidente λ de 200 nm a 400 nm para simular as forças ópticas exercidas na nanocápsula. Como o FETI-DP trabalha no domínio da frequência, as forças ópticas são calculadas em 15 pontos de frequência de amostragem. A Figura 4 mostra a curva calculada das forças ópticas exercidas na nanocápsula de prata. Para indicar a precisão do FETI-DP, os resultados da força óptica do FETI-DP são comparados com os do software comercial Lumerical FDTD Solutions [33], e pode-se observar uma boa concordância.

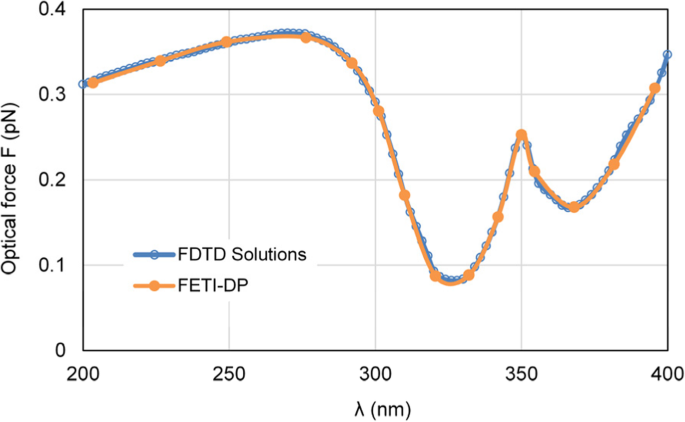
Resultados das forças ópticas exercidas na nanocápsula de prata, variando com o comprimento de onda λ de luz incidente, incluindo os resultados do FETI-DP e as soluções de software comercial FDTD

Em seguida, o desempenho do FETI-DP é testado para diferentes números de subdomínios. Aumentamos o número de subdomínios de 4 para 24, mantendo a densidade de discretização. Atribuímos cada processador para lidar com um subdomínio. Table 1 reports the time used for the construction of global interface Eq. (6) and the total solution time. It can be seen that the FETI-DP can fully exploit parallel computing resources and significantly improve the solution efficiency. Besides, the accuracy of the FETI-DP with the number of subdomains increasing is also examined and reported in Table 1. Here, the accuracy is defined by the 2-norm relative error of the optical force as δ _OF = ‖OF _i − OF _ref ‖/‖OF _ref ‖, where OF _i is the optical force using i subdomains and OF _ref denotes the reference optical force using two subdomains. It can be seen that the accuracy keeps almost constant with the number of subdomains increasing.

Gold Nanosphere Dimer

The second example analyzes the optical trapping of a gold nanosphere by using a gold nanosphere dimer. The plasmonic effects at the dimer gap can effectively enhance the optical force for trapping nanoparticle. Figure 5 a and b gives the configuration and dimensions of this system. The constitutive parameters of gold are all measured values taken from [32]. The surrounding medium is water with a relative refractive index of n = 1.33. The incident light is a plane wave with the power of 10 mW/μm² , the electric field polarization direction is +x , and the incident direction is −z . The optical force exerted on the object nanosphere is calculated by the FETI-DP method. For the FETI-DP implementation, the whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which results in 3.5 × 10⁶ unknowns, including 1.6 × 10⁵ dual unknowns and 1738 corner unknowns.

Configuration of an optical trapping system of a gold nansphere dimer in water. a 3D view. b Front view and dimensions, where R = 25 nm, r = 5 nm, and g = 2 nm

First, we test the parallel performance of the proposed FETI-DP by using various numbers of processors. Table 2 reports the solution time for Eq. (6) as well as the total solution time. Besides, the speedups for the parallel computation are also provided in Table 2. Here, the speedup is defined by
$$ \mathrm{Speed}\ \mathrm{up}=\raisebox{1ex}{${T}_1$}\!\left/ \!\raisebox{-1ex}{${T}_{N_p}$}\right. $$ (17)
where $ {T}_{N_p} $ denotes the total wall-clock time using N _p processors. It can be seen that the FETI-DP significantly improves the solution efficiency and exhibits good parallel speedup. For this large number of unknowns, the total memory usage of all the processors is only 57.2 GB.

Then, the effectiveness of the low-rank sparsification approach is examined. With the low-rank sparsification, the subdomain matrix can be factorized by data-sparse algorithm and stored as data-sparse matrices. The construction time and memory usage are only 18 s and 0.5 GB, while they are 67 s and 1.7 GB by conventional matrix algorithm. It can be seen that we get 72% time saving and 70% memory compression. Related to the memory usage, the subsequent MVPs can also get 70% time-saving.

Next, the FETI-DP is tested for the optical force calculation with the wavelength λ varying from 277 nm to 818 nm. In practice, the analyses of optical force under incident light of different wavelengths are often necessary for searching the plasmonic resonance wavelength, where drastic field enhancement occurs and the strongest optical force can be obtained. Two cases are considered with the nanosphere located at (0, 0, 20 nm) and (0, 0, − 20 nm). Figure 6 a and b plots the calculated optical forces exerted on the nanosphere for different λ . It can be seen that the maximum optical force occurs at λ = 472 nm, which is the plasmonic resonance wavelength. The optical force at this resonance wavelength enhanced by nearly 40 times as against that at non-resonance wavelength. Moreover, the optical force always points to the dimer gap, as shown in Fig. 6, where the electric field intensity is strongest. It is also the direction of gradient force to trap the object. Figure 7 a and b shows the calculated electric field enhancement distributions at the non-resonance wavelength of λ = 300 nm and the resonance wavelength of λ = 472 nm, respectively. It can be seen that the electric field intensity has been increased by almost 250 times due to the plasmonic resonance effect.

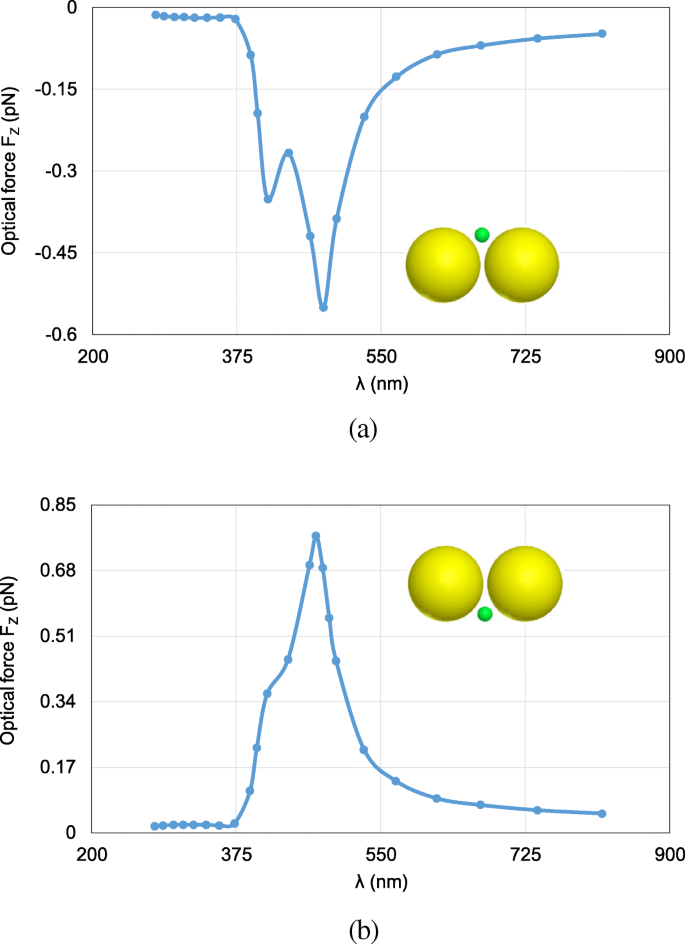
Calculated results of optical forces exerted on the nanosphere in the system of gold nanosphere dimer, varying with the wavelength λ of incident light. a The object nanosphere is located at (0, 0, 20 nm). b The object nanosphere is located at (0, 0, − 20 nm)

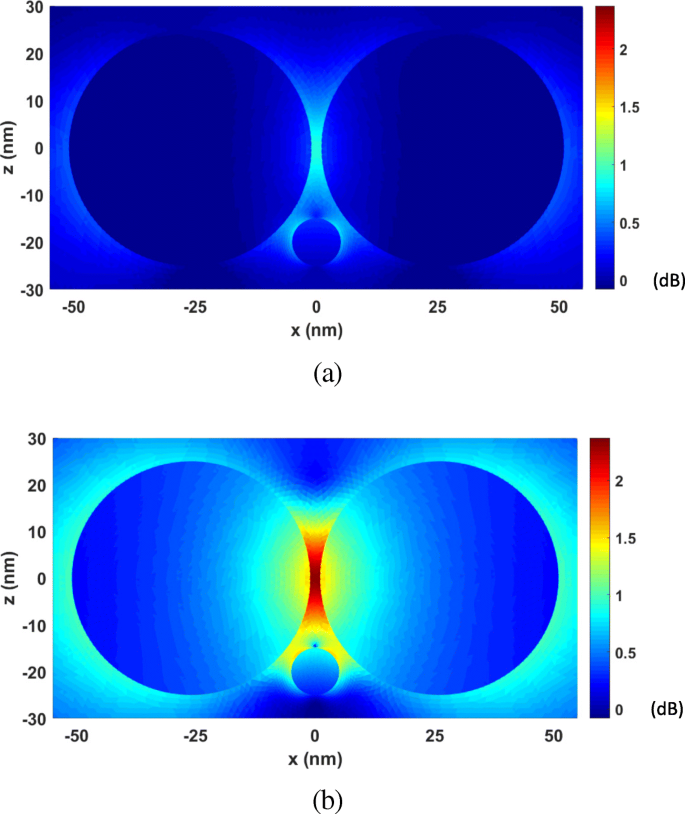
The electric field enhancement distributions on the xoz plane for the system of gold nanosphere dimer. a λ = 300 nm (non-resonance wavelength). b λ = 472 nm (resonance wavelength)

Besides, the optical force and optical potential are calculated with the nanosphere moving from (0, 0, − 30 nm) to (0, 0, − 17 nm) along the z -eixo. Since the most typical and interesting behavior of trapping forces and potentials are those acting along z -direction, we here consider the axial trapping potential by integration along the z -eixo. Because the motion of the nanoparticle is restricted to one dimension, the definition of an optical potential is unambiguous from (16), even though the total optical force from (15) is non-conservative. As shown in Fig. 8 a, b, with the nanosphere moving to the dimer gap, the optical force and optical potential depth obviously increase. At the position of (0, 0, − 17 nm), an optical potential depth of 4.6 k _B T is produced, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

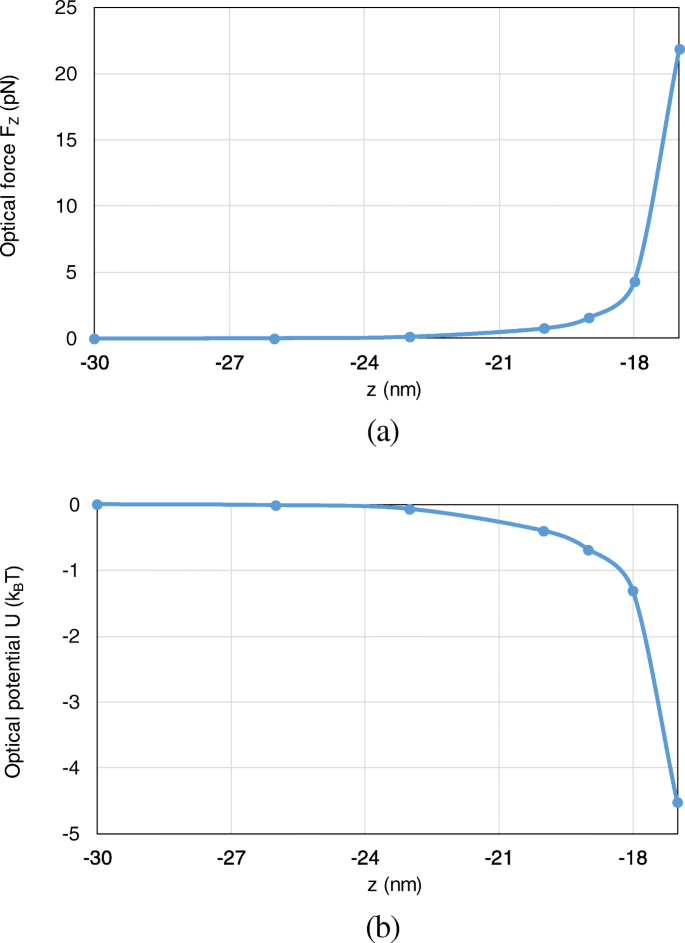
The optical forces and optical potentials exerted on the nanosphere in the system of gold nanosphere dimer, when the nanosphere moves from (0, 0, − 30 nm) to (0, 0, − 17 nm). a The optical forces. b The optical potentials

Finally, we test the effects of the dielectric substrate for this example. The optical forces are calculated with and without a substrate, respectively. For both two cases, the nanosphere is located at (0, 0, − 20 nm) and the incident wavelength is chosen as the resonance wavelength. For the case without substrate, the calculated result of the optical force is |F ₀ | = 0.769 pN. For the case with a substrate, the gold nanosphere dimer is put on a dielectric substrate with a thickness of 60 nm and a relative permittivity of ε _r = 2.25. The calculated result of the optical force is |F ₁ | = 0.761 pN. The relative error between these two results of optical forces is about 1.0 × 10⁻² , which is defined as |F ₁ − F ₀ |/|F ₀ |

Gold Truncated Cone Dimer

The third example deals with the optical trapping of a gold nanosphere by using a gold truncated cone dimer. Figure 9 gives the configuration and dimensions of this system. The constitutive parameters of gold are taken from [32]. The dielectric substrate has a relative permittivity of ε _r = 2.25. The surrounding medium is water with a relative refractive index of n = 1.33. The incident light is plane wave with the power of 10 mW/μm² , the electric field polarization direction is +x , and the incident direction is −z . The whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which leads to 3.1 × 10⁶ unknowns, including 1.3 × 10⁵ dual unknowns and 1227 corner unknowns.

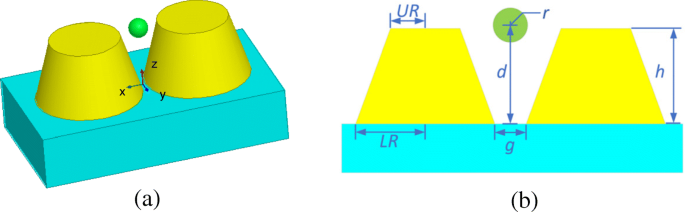
Configuration of an optical trapping system of a gold truncated cone dimer based on a dielectric substrate in water. a 3D view. b Front view and dimensions, where UR = 20 nm, LR = 30 nm, h = 35 nm, and g = 2 nm

First, we analyze the optical forces by changing λ from 277 nm to 818 nm. Figure 10 plots the calculated optical forces exerted on the nanosphere for different λ . The nanosphere is located at (0, 0, 35 nm). It can be seen that the maximum optical force occurs at λ = 464 nm, which is the plasmonic resonance wavelength, and the optical force here is enhanced by nearly 30 times at non-resonance wavelength. Moreover, the total optical force always points to −z , as shown in Fig. 10, which is the direction of the gradient force. This confirms that the gradient force is greater than the scattering force, which is one of the conditions that the nanosphere can be stably trapped. Figure 11 a and b presents the calculated electric field distributions at the non-resonance wavelength of λ =300 nm and the resonance wavelength of λ = 464 nm, respectively. It can be seen that electric field intensity has been increased by almost 500 times due to the localized surface plasmon resonance.

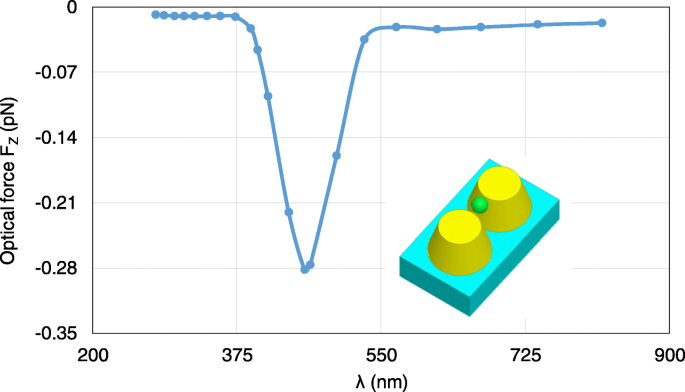
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer, varying with λ . The nanosphere is located at (0, 0, 35 nm)

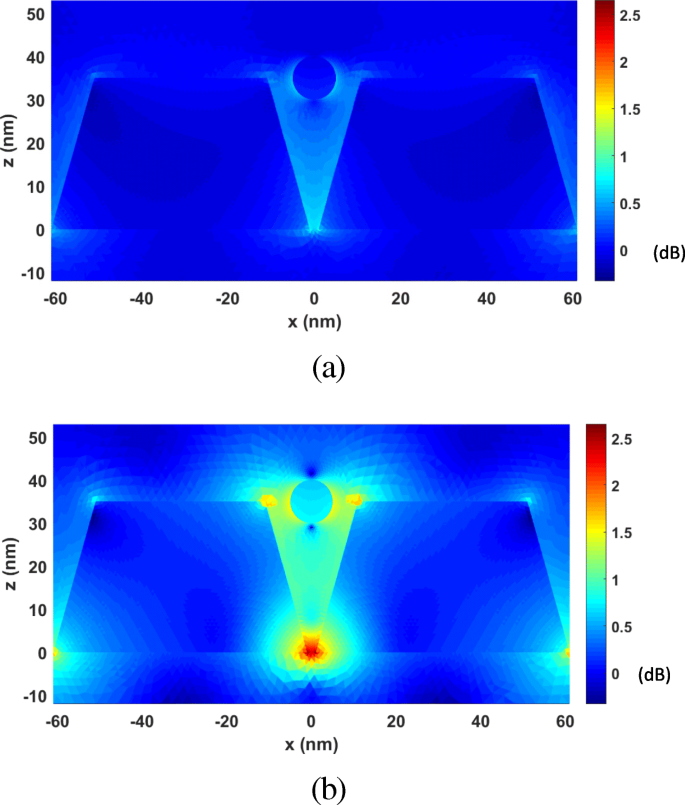
The electric field enhancement distributions on the xoz plane for the system of gold truncated cone dimer. a λ =300 nm (non-resonance wavelength). b λ =464 nm (resonance wavelength)

Then, the location of the nanosphere is changed to 0, 5, and 35 nm to observe the optical force. Figure 12 gives the calculated optical forces exerted on the nanosphere, where obvious y -component of optical force can be observed, while greater z -component of optical force exists. The total optical force still points to the position with the strongest electric field to trap the nanosphere.

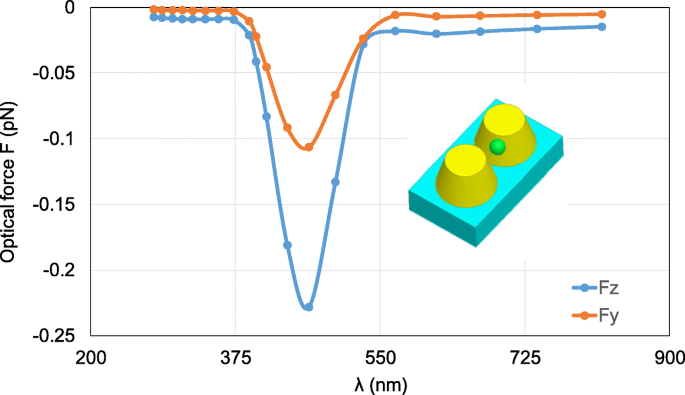
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer varying λ . The nanosphere is located at (0, 5 nm, 35 nm)

Furthermore, we analyze the optical potential with the nanosphere moving from (0, 0, 50 nm) to (0, 0, 20 nm) along the z -eixo. Here, we consider the axial trapping potential along z -direction, which restricts the motion of the nanoparticle to one dimension and leads to an unambiguous definition of optical potential. Both the optical force and potential are calculated. As can be observed from Fig. 13 a, b, with the nanosphere moving to the dimer gap, the optical force and the optical potential depth obviously increase. At (0, 0, 20 nm), an optical potential depth of 3.8 k _B T is obtained, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

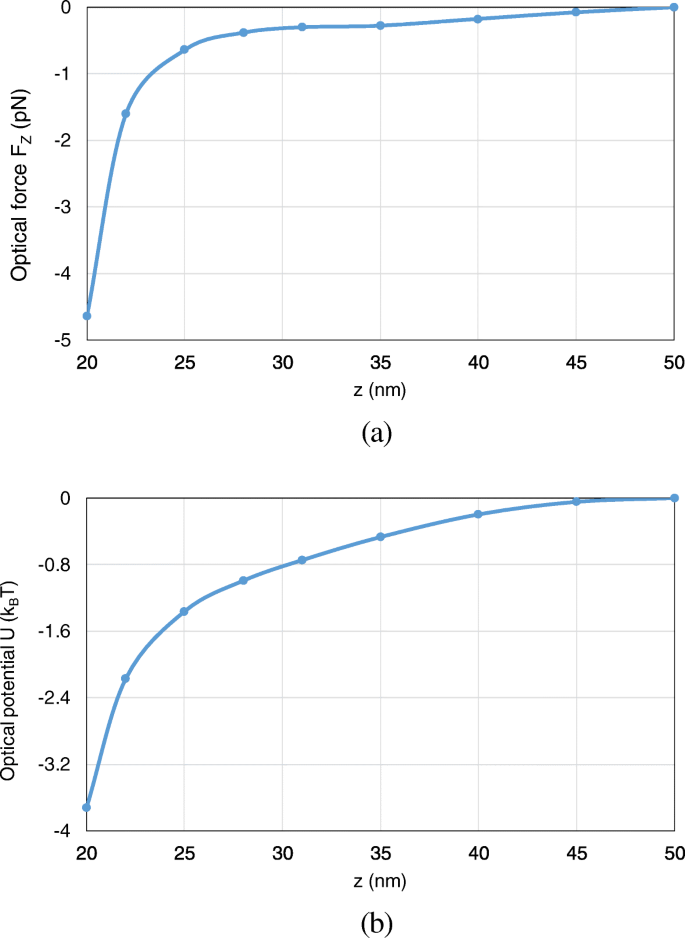
The optical forces and optical potentials exerted on the nanosphere in the system of gold truncated cone dimer, when the nanosphere moves from (0, 0, 50 nm) to (0, 0, 20 nm). a The optical forces. b The optical potentials

Finally, we test the computational costs of the FETI-DP by changing the number of unknowns from 1.0 million to 3.2 million based on different mesh size. In practice, the tests under different mesh density are usually necessary to meet different accuracy requirements. Such a large-scale complex problem brings great challenges to conventional numerical methods. However, the FETI-DP can easily handle this problem. Thirty-two processors are employed for the FETI-DP simulation, while each processor deals with a subdomain. Table 3 reports the computational costs of the FETI-DP. It can be seen that the FETI-DP exhibits high simulation efficiency and low memory requirement.

Conclusão

An FETI-DP method combined with low-rank sparsification is proposed for the prediction and analysis of optical trapping of metal nanoparticles. The proposed method provides fully decoupled subdomain problems, which converts a large-scale complex problem into a series of small-scale simple problems. It is well-suited for parallel computation and can significantly improve the efficiency of numerical simulation. Examples demonstrate that the proposed method exhibits excellent performance of large-scale computation and is well-suited for the fast and accurate simulation of optical trapping at nanoscale.

Disponibilidade de dados e materiais

All data generated or analyzed during this study are included in this article.

Abreviações

ABC:: Absorbing boundary condition
DOF:: Degrees of freedom
FDTD:: Domínio do tempo de diferença finita
FEM:: Finite element method
FETI-DP:: Dual-primal finite element tearing and interconnecting
MST:: Maxwell stress tensor
MVP:: Matrix-vector product

Relações matemáticas mágicas para nanoclusters - errata e adendo Nanohelix de porta dupla como uma nova superrede binária ajustável

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias