Solução Minterm vs Maxterm

Até agora, temos encontrado soluções de Soma de Produto (SOP) para problemas de redução lógica. Para cada uma dessas soluções SOP, há também uma solução Product-Of-Sums (POS), que pode ser mais útil, dependendo da aplicação.

Antes de trabalhar com uma solução Product-Of-Sums, precisamos apresentar algumas novas terminologias. O procedimento abaixo para mapear os termos do produto não é novo neste capítulo.

Queremos apenas estabelecer um procedimento formal para mintermos para comparação com o novo procedimento para maxtermos.







Minterm

Um mintermo é uma expressão booleana resultando em 1 para a saída de uma única célula, e 0 s para todas as outras células em um mapa de Karnaugh, ou tabela verdade. Se um mintermo tiver um único 1 e as células restantes como 0 s, parece cobrir uma área mínima de 1 s.

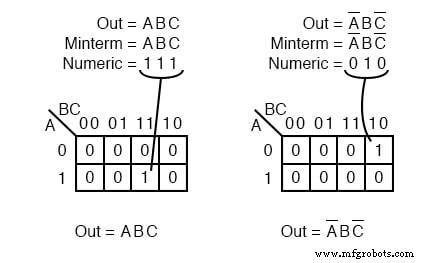
A ilustração acima à esquerda mostra o mintermo ABC , um único termo de produto, como um único 1 em um mapa que é 0 s. Não mostramos o 0 s em nossos mapas de Karnaugh até este ponto, visto que é costume omiti-los, a menos que seja especificamente necessário. Outro mintermo A’BC ’ é mostrado acima à direita.

O ponto a ser revisto é que o endereço da célula corresponde diretamente ao mintermo que está sendo mapeado. Ou seja, a célula 111 corresponde ao mintermo ABC acima à esquerda.

Acima à direita, vemos que o mintermo A’BC ’ corresponde diretamente à célula 010 . Uma expressão ou mapa booleano pode ter vários mintermos.

Referindo-nos à figura acima, vamos resumir o procedimento para colocar um mintermo em um K-map:

• Identifique o termo do mintermo (termo do produto) a ser mapeado.
• Escreva o valor numérico binário correspondente.
• Use o valor binário como um endereço para colocar um 1 no K-map
• Repita as etapas para outros mintermos (termos P em uma soma de produtos).

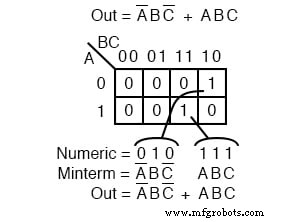
Uma expressão booleana mais frequentemente do que não consistirá em vários mintermos correspondendo a várias células em um mapa de Karnaugh como mostrado acima. Os vários mintermos neste mapa são os mintermos individuais que examinamos na figura anterior acima.

O ponto que revisamos para referência é que o 1 s saem do K-map como um endereço de célula binário que converte diretamente em um ou mais termos de produto.

Diretamente, queremos dizer que um 0 corresponde a uma variável complementada, e um 1 corresponde a uma variável verdadeira. Exemplo: 010 converte diretamente para A’BC ’ .

Não houve redução neste exemplo. Porém, temos um resultado de Soma de Produtos dos mintermos.

Referindo-nos à figura acima, vamos resumir o procedimento para escrever a equação booleana reduzida da Soma dos Produtos a partir de um K-map:

• Forme grupos maiores de 1 s possível cobrindo todos os mintermos. Os grupos devem ser uma potência de 2.
• Escreva o valor numérico binário para os grupos.
• Converta o valor binário em um termo de produto.
• Repita as etapas para outros grupos. Cada grupo produz um p-termos em uma Soma de Produtos.

Nada de novo até agora, um procedimento formal foi escrito para lidar com mintermos. Isso serve como um padrão para lidar com maxtermos.

Em seguida, atacamos a função booleana que é 0 para uma única célula e 1 s para todos os outros.







Maxterm

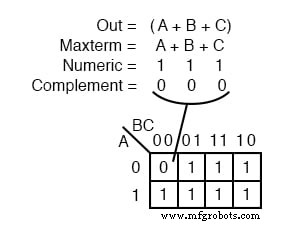
Um maxterm é uma expressão booleana resultando em um 0 para a saída de uma única expressão de célula e 1 s para todas as outras células no mapa de Karnaugh, ou tabela verdade. A ilustração acima à esquerda mostra o maxterm (A + B + C) , um único termo de soma, como um único 0 em um mapa que é 1 s.

Se um maxterm tiver um único 0 e as células restantes como 1 s, parece cobrir uma área máxima de 1 s.

Existem algumas diferenças agora que estamos lidando com algo novo, maxtermos. O maxterm é um 0 , não um 1 no mapa de Karnaugh. Um maxtermo é um termo de soma, (A + B + C) em nosso exemplo, não um termo de produto. Também parece estranho que (A + B + C) está mapeado na célula 000 .

Para a equação Out =(A + B + C) =0 , todas as três variáveis ​​ (A, B, C) deve ser individualmente igual a 0 . Apenas (0 + 0 + 0) =0 será igual a 0 . Assim, colocamos nosso único 0 para mintermo (A + B + C) na célula A, B, C =000 no K-map, onde as entradas são todas 0 .

Este é o único caso que nos dará um 0 para o nosso maxterm. Todas as outras células contêm 1 s porque qualquer valor de entrada diferente de ( (0,0,0) para (A + B + C) rende 1 s após avaliação.

Referindo-se à figura acima, o procedimento para colocar um maxterm no K-map é:

• Identifique o termo de Soma a ser mapeado.
• Escreva o valor numérico binário correspondente.
• Forme o complemento
• Use o complemento como um endereço para colocar um 0 no K-map
• Repita para outros maxtermos (termos de soma na expressão Produto das somas).

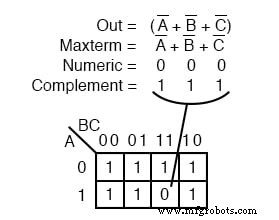
Outro maxtermo A ’+ B’ + C ’ é mostrado acima. Numérico 000 corresponde a A ’+ B’ + C ’ . O complemento é 111 . Coloque um 0 para maxterm (A ’+ B’ + C ’) nesta célula (1,1,1) do K-map conforme mostrado acima.

Por que deveria (A ’+ B’ + C ’) causar um 0 estar na célula 111 ? Quando A ’+ B’ + C ’ é (1 ’+ 1’ + 1 ’) , todos 1 s in, que é (0 + 0 + 0) depois de receber os complementos, temos a única condição que nos dará um 0 . Todos os 1 s são complementados com todos os 0 s, que é 0 quando OU ed.







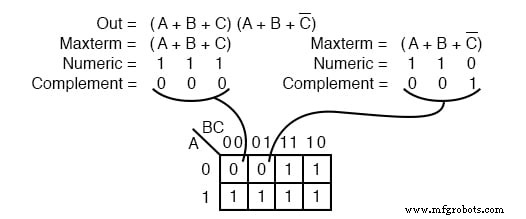
Uma expressão ou mapa Boolean Product-Of-Sums pode ter vários maxtermos, conforme mostrado acima. Maxterm (A + B + C) produz 111 numérico que complementa a 000 , colocando um 0 na célula (0,0,0) . Maxterm (A + B + C ’) produz 110 numérico que complementa a 001 , colocando um 0 na célula (0,0,1) .

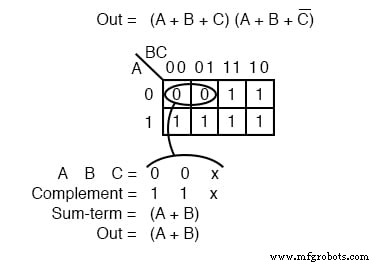
Agora que temos a configuração do k-map, o que realmente nos interessa é mostrar como escrever uma redução do produto das somas. Forme o 0 s em grupos. Isso seria um grupo de dois abaixo. Escreva o valor binário correspondente ao termo da soma que é (0,0, X) .

Ambos A e B são 0 para o grupo. Mas, C é ambos 0 e 1 então escrevemos um X como um marcador de posição para C . Forme o complemento (1,1, X) . Escreva o termo de soma (A + B) descartando o C e o X que ocupou o seu lugar.

Em geral, espere ter mais termos de soma multiplicados juntos no resultado Produto-das-somas. Porém, temos um exemplo simples aqui.







Vamos resumir o procedimento para escrever a redução booleana do produto das somas para um K-map:

• Forme grupos maiores de 0 s possível, cobrindo todos os maxtermos. Os grupos devem ser uma potência de 2.
• Escreva o valor numérico binário para o grupo.
• Complemente o valor numérico binário para o grupo.
• Converta o valor do complemento em um termo de soma.
• Repita as etapas para outros grupos. Cada grupo produz um termo de soma em um resultado de Produto das somas.

Exemplos

Exemplo:

Simplifique a expressão booleana Product-Of-Sums abaixo, fornecendo um resultado no formato POS.







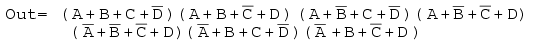
Solução:

Transfira os sete maxtermos para o mapa abaixo como 0 s. Certifique-se de complementar as variáveis ​​de entrada para encontrar a localização adequada da célula.







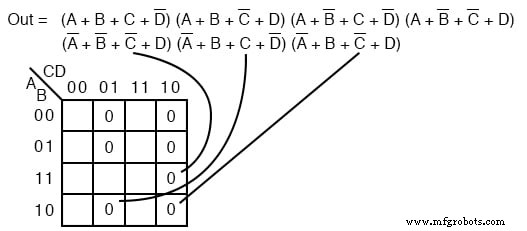
Nós mapeamos o 0 s conforme aparecem da esquerda para a direita, de cima para baixo no mapa acima. Localizamos os últimos três maxtermos com linhas líderes.

Uma vez que as células estão no lugar acima, forme grupos de células como mostrado abaixo. Grupos maiores darão um termo de soma com menos entradas. Menos grupos produzirão menos termos de soma no resultado.







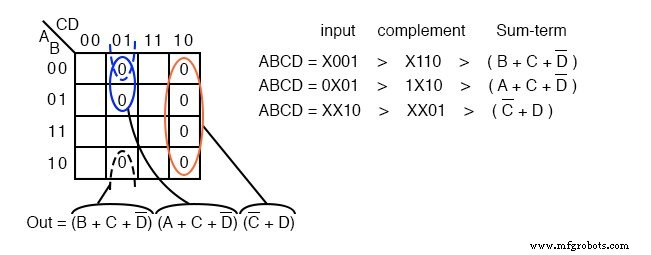
Temos três grupos, portanto esperamos ter três termos de soma em nosso resultado de PDV acima. O grupo de 4 células produz um termo de soma de 2 variáveis. Os dois grupos de 2 células nos dão dois termos de soma de 3 variáveis.

Os detalhes são mostrados sobre como chegamos aos termos de soma acima. Para um grupo, escreva o endereço de entrada do grupo binário e, em seguida, complemente-o, convertendo-o no termo de soma booleano. O resultado final é produto das três somas.

Exemplo:

Simplifique a expressão booleana Product-Of-Sums abaixo, fornecendo um resultado na forma SOP.











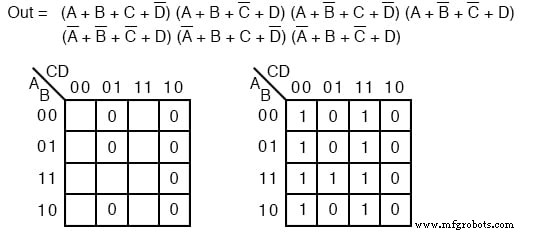
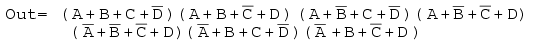
Solução: Isso parece uma repetição do último problema. Exceto que pedimos uma Solução de Soma de Produtos em vez do Produto de Soma que acabamos de terminar. Mapeie o maxterm 0 s do Produto-das-somas dados como no problema anterior, abaixo à esquerda.







Em seguida, preencha o 1 implícito s nas células restantes do mapa acima à direita.







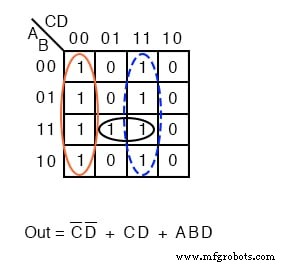
Formar grupos de 1 s para cobrir todos 1 s. Em seguida, escreva o resultado simplificado da Soma de Produtos como na seção anterior deste capítulo. Isso é idêntico a um problema anterior.







Acima, mostramos a solução Product-Of-Sums, do exemplo anterior, e a solução Soma-Of-Products do problema atual, para comparação.

Qual é a solução mais simples? O POS usa portas 3-OR e porta 1-AND, enquanto o SOP usa portas 3-AND e porta 1-OR. Ambos usam quatro portas cada.

Olhando mais de perto, contamos o número de entradas de porta. O POS usa 8 entradas; o SOP usa 7 entradas. Pela definição de solução de custo mínimo, a solução SOP é mais simples.

Este é um exemplo de resposta tecnicamente correta que é de pouca utilidade no mundo real.

A melhor solução depende da complexidade e da família lógica que está sendo usada. A solução SOP geralmente é melhor se usar a família lógica TTL, já que as portas NAND são o bloco de construção básico, que funciona bem com implementações SOP.

Por outro lado, uma solução POS seria aceitável ao usar a família de lógica CMOS, uma vez que todos os tamanhos de portas NOR estão disponíveis.







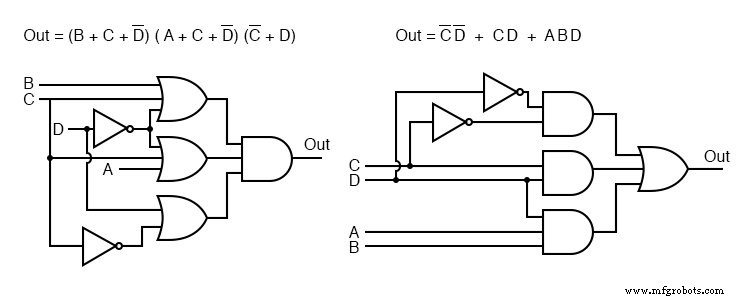
Os diagramas de passagem para ambos os casos são mostrados acima, Produto das somas à esquerda e Soma dos produtos à direita.

Abaixo, damos uma olhada mais de perto na versão Soma-de-Produtos de nossa lógica de exemplo, que é repetida à esquerda.







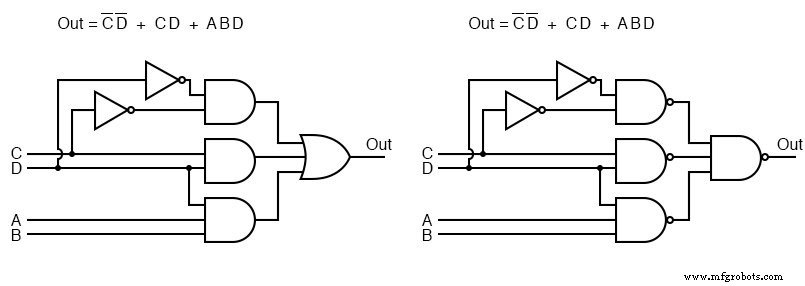
Acima de todas as portas AND à esquerda foram substituídas por portas NAND à direita. A porta OR na saída foi substituída por uma porta NAND. Para provar que a lógica AND-OR é equivalente à lógica NAND-NAND, mova as bolhas invertidas do inversor na saída das portas 3-NAND para a entrada do NAND final, conforme mostrado indo de cima à direita para baixo à esquerda.







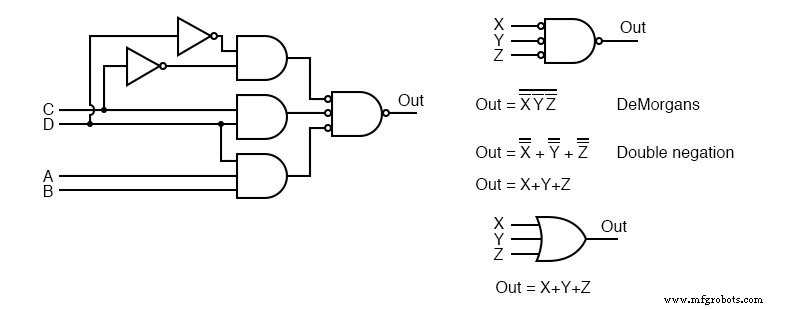
Acima à direita, vemos que a porta NAND de saída com entradas invertidas é logicamente equivalente a uma porta OR pelo teorema de DeMorgan e negação dupla.

Esta informação é útil na construção de lógica digital em um ambiente de laboratório onde as portas NAND da família lógica TTL estão mais prontamente disponíveis em uma ampla variedade de configurações do que outros tipos.

O procedimento para construir a lógica NAND-NAND, no lugar da lógica AND-OR, é o seguinte:

• Produza um design lógico de soma de produtos reduzido.
• Ao desenhar o diagrama de fiação do SOP, substitua todas as portas (AND e OR) por portas NAND.
• As entradas não utilizadas devem ser vinculadas à lógica Alta.
• Em caso de solução de problemas, os nós internos no primeiro nível de saídas da porta NAND NÃO correspondem aos níveis lógicos do diagrama AND-OR, mas são invertidos. Use o diagrama lógico NAND-NAND. No entanto, as entradas e a saída final são idênticas.
• Rotule quaisquer pacotes múltiplos U1, U2, .. etc.
• Use a planilha de dados para atribuir números de pinos às entradas e saídas de todos os portões.

Exemplo:

Vamos revisitar um problema anterior envolvendo uma minimização de SOP. Produza uma solução Produto-das-somas. Compare a solução POS com o SOP anterior.







Solução:

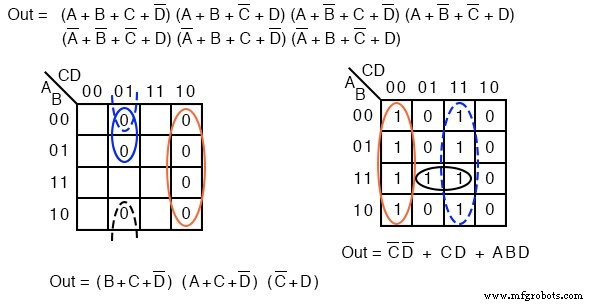
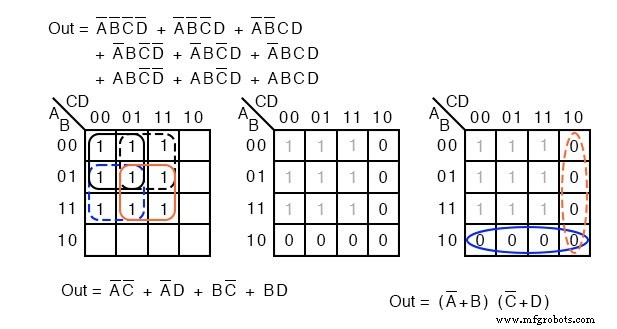
Acima, à esquerda, temos o problema original começando com uma expressão booleana não simplificada de 9 minutos. Revendo, formamos quatro grupos de 4 células para produzir um resultado SOP de 4 produtos-termo, parte inferior esquerda.

Na figura do meio, acima, preenchemos os espaços vazios com o 0 implícito s. O 0 s formam dois grupos de 4 células. O grupo azul sólido é (A ’+ B) , o grupo vermelho tracejada é (C ’+ D) . Isso produz dois termos de soma no resultado do Produto das somas, acima à direita Fora =(A ’+ B) (C’ + D)

Comparando a simplificação do SOP anterior, à esquerda, com a simplificação do POS, à direita, mostra que o POS é a solução de menor custo. O SOP usa 5 portas no total, o POS usa apenas 3 portas.

Esta solução POS parece atraente até mesmo ao usar a lógica TTL devido à simplicidade do resultado. Podemos encontrar portas AND e uma porta OR com 2 entradas.







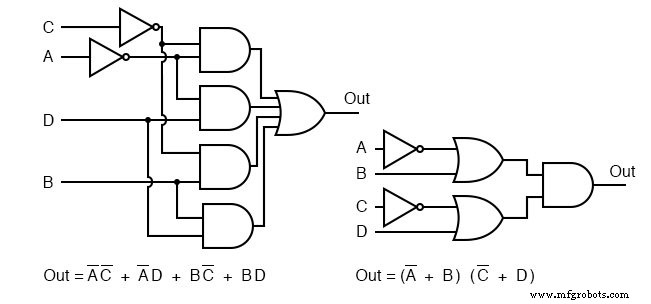
Os diagramas de portas SOP e POS são mostrados acima para nosso problema de comparação.

Dadas as pinagens para as portas de circuito integrado da família lógica TTL abaixo, rotule o diagrama maxterm acima à direita com os designadores de circuito (U1-a, U1-b, U2-a, etc.) e os números dos pinos.







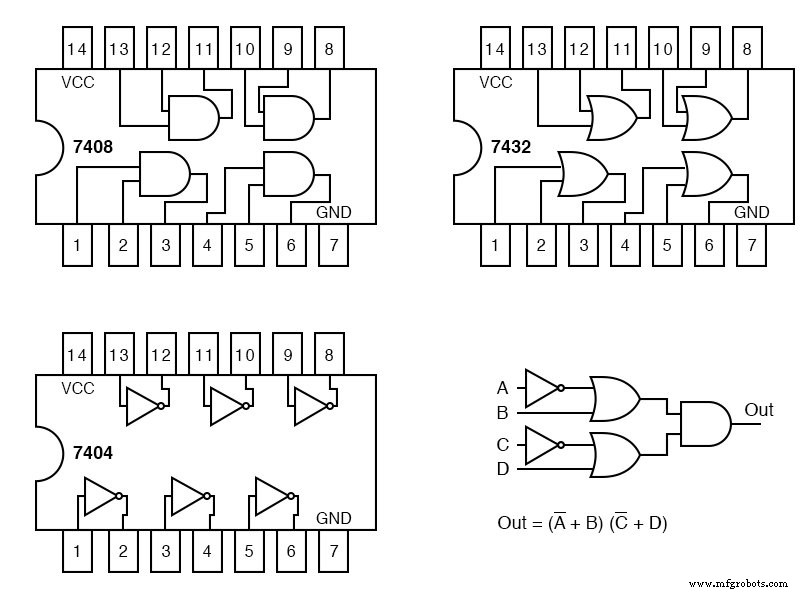
Cada pacote de circuito integrado que usarmos receberá um designador de circuito:U1, U2, U3. Para distinguir entre as portas individuais dentro do pacote, elas são identificadas como a, b, c, d, etc.

O pacote do inversor hexadecimal 7404 é U1. Os inversores individuais nele são U1-a, U1-b, U1-c, etc. U2 é atribuído ao 7432 quad OR gate. U3 é atribuído ao 7408 quad AND gate.

Com referência aos números de pinos no diagrama de pacote acima, atribuímos números de pinos a todas as entradas e saídas de porta no diagrama esquemático abaixo.

Agora podemos construir este circuito em um ambiente de laboratório. Ou podemos projetar uma placa de circuito impresso para isso. Uma placa de circuito impresso contém “fiação” de folha de cobre apoiada por um substrato não condutor de fenólico ou fibra de vidro epóxi.

As placas de circuito impresso são usadas para a produção em massa de circuitos eletrônicos. Aterre as entradas de portas não utilizadas.







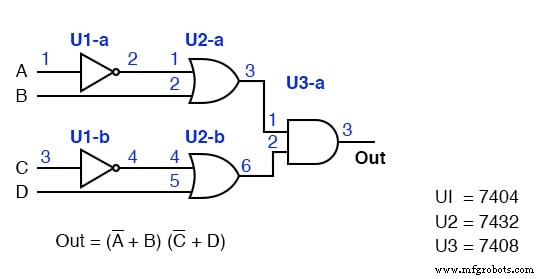
Identifique o diagrama de solução POS anterior acima à esquerda (terceira figura atrás) com designadores de circuito e números de pinos. Isso será semelhante ao que acabamos de fazer.







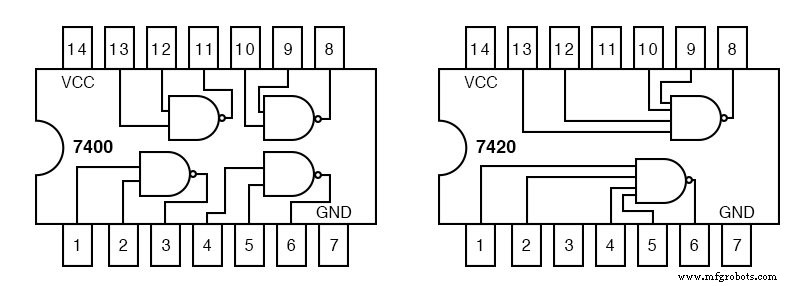
Podemos encontrar portas AND de 2 entradas, 7408 no exemplo anterior. No entanto, temos problemas para encontrar uma porta OR de 4 entradas em nosso catálogo TTL.

O único tipo de porta com 4 entradas é a porta 7420 NAND mostrada acima, à direita.

Podemos transformar a porta NAND de 4 entradas em uma porta OR de 4 entradas invertendo as entradas para a porta NAND como mostrado abaixo. Portanto, usaremos a porta NAND de 4 entradas do 7420 como uma porta OR, invertendo as entradas.







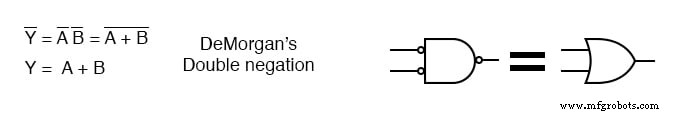
Não usaremos inversores discretos para inverter as entradas para a porta NAND de 4 entradas 7420, mas iremos acioná-lo com portas NAND de 2 entradas no lugar das portas AND exigidas na solução SOP, mintermo.

A inversão na saída das portas NAND de 2 entradas fornece a inversão da porta OR de 4 entradas.







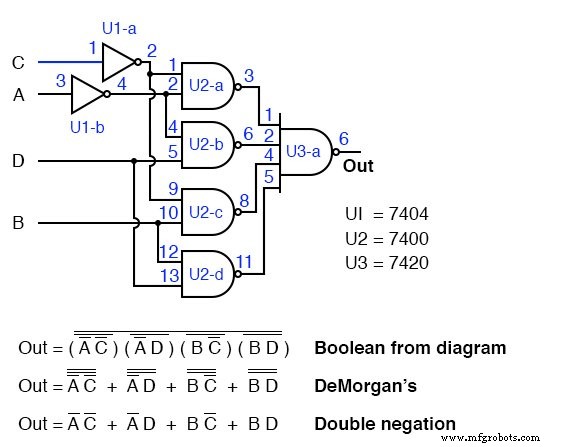
O resultado é mostrado acima. É a única maneira prática de realmente construí-lo com portas TTL usando a lógica NAND-NAND em substituição à lógica AND-OR.



PLANILHAS RELACIONADAS:

• Planilha de mapeamento de Karnaugh