Ângulos de Euler do robô:a cartilha essencial

É difícil entender as rotações do robô, não é? Os ângulos de Euler são uma dor no pescoço. Aqui está a cartilha essencial para tirar a dor.

Orientações! Eles só me fazem querer arrancar meu cabelo. Se você já teve que programar a pose final de um robô usando coordenadas e rotações, sabe do que estou falando.

À primeira vista, definir a pose do efetor final do seu robô parece simples, não é?

Você simplesmente diz "Quero mover a ferramenta do robô para isto localização e quero que ela aponte neste direção."

Intuitivamente, você sabe exatamente qual orientação deseja que a ferramenta tenha. No entanto, quando se trata de descrever a orientação usando números precisos, de repente essa tarefa simples se torna uma confusão.

Por que as orientações do robô são difíceis de entender

É fácil descrever as coordenadas X, Y, Z (translacionais) da ferramenta de um robô.

Para descrever uma tradução, basta inserir as coordenadas — ex. Point[X, Y, Z] =[100, 1000, 1500] mm — e há apenas um local ao qual isso pode se referir, supondo que você esteja usando a mesma referência de base. Pode significar apenas 100 mm ao longo do eixo X, 1 metro ao longo do eixo Y e 1,5 metros ao longo do eixo Z.

Mas, como você descreve a orientação da ferramenta?

Você poderia dizer:
Rotação[XYZ] =[5, 45, 15]°
no entanto, você também poderia dizer (arredondando os números)
Rot[XY'Z”] =[-7,9, 44,7, 16,2]°
ou
Rot[ZY'Z”] =[7,9, 45,2, 5,0]°
ou mesmo
Quaternion[q1-q4] =[0,9, -0,1, 0,4, 0,1]

 Tudo isso se refere exatamente à mesma orientação!
O que torna ainda mais impressionante é que diferentes fabricantes de robôs usam convenções diferentes. Tudo pode se tornar uma dor de cabeça, mesmo quando você está familiarizado com a geometria 3D.

O problema:simplesmente não pensamos em rotações

O verdadeiro problema é que não pensamos naturalmente em termos de rotações.

Entendemos intuitivamente as coordenadas de tradução porque as usamos em nossa vida cotidiana (por exemplo, “Está na segunda prateleira abaixo, quatro livros da esquerda.” ). No entanto, quando temos que descrever uma orientação, recorremos a apontar com o dedo e dizer “É nessa direção”.

Infelizmente, os robôs precisam de informações mais precisas do que um vago “está ali.”

O que precisamos é uma compreensão sólida dos Ângulos de Euler.

O que são ângulos de Euler?

Vamos dar um passo atrás e começar com o básico.

O método mais comum para descrever as orientações do robô são os Ângulos de Euler. Ângulos de Euler consiste em três números, cada um descrevendo uma rotação em torno de um eixo. Existem diferentes convenções de ângulo de Euler, dependendo da ordem das rotações.

Primeiro, vamos simplificar isso para um exemplo de um eixo.

Imagine uma bússola.

Muitas vezes, o eixo Z do mundo se refere ao eixo que se estende do céu ao chão. Então, você pode pensar na agulha de uma bússola sendo uma rotação em torno do eixo Z (chamada Rot[Z]). Quando você segura a bússola à sua frente e a seta aponta para 135°, significa que o Norte está sobre seu ombro esquerdo, então você está voltado para o Sudeste. Não importa onde você coloque a bússola (no chão, na cabeça, etc) se ela tiver a mesma orientação, o ângulo será sempre de 135°.

Até agora, tão simples.

Nossa bússola tem apenas um valor de rotação (ou seja, Rot[Z]), mas para descrever qualquer orientação 3D precisamos de três valores. É aqui que começa a ficar um pouco mais complicado.

Outros métodos para descrever as orientações do robô são Quaternions ou Poses (matrizes 4×4).

Vamos começar a trabalhar

De agora em diante, será útil ter um auxílio visual interativo.

Eu sugiro que você baixe uma cópia gratuita do RoboDK neste link, o que torna muito fácil visualizar os referenciais e ver as coordenadas resultantes.

Inicie o RoboDK e crie um quadro de referência usando o botão “Adicionar quadro de referência” ou selecionando a opção no menu Programa. Você deve ver um quadro vermelho, verde e azul aparecer no meio da tela.

Você pode girar o quadro assim:mantenha pressionada a tecla Alt, clique e arraste uma das setas curvas que aparecem.

Como pilotar um avião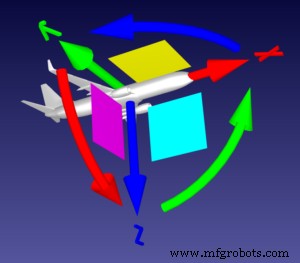

Vamos usar a analogia de um avião, conforme descrito muito claramente no fórum de robôs.

Imagine que o referencial é um plano. A ponta da seta reta vermelha (o eixo X) é a ponta de seu nariz-cone e a seta reta verde (o eixo Y) é sua asa esquerda.

Nesse caso, mover as setas curvas tem as seguintes funções:

• Seta vermelha curva =Rot[X]:O Roll do avião, que permite que o avião gire em torno de seu eixo horizontal.
• Seta verde curva =Rot[Y]:O Pitch do avião, que aponta o nariz-cone para cima ou para baixo.
• Seta azul curva =Rot[Z]:a guinada do avião, que determina a direção em que o avião está indo.

Se o piloto quisesse que o avião virasse para a esquerda e para baixo, gradualmente, o avião não giraria apenas no eixo Z - não é assim que os aviões funcionam.

Em vez disso, o avião iria:

1. Abaixe o cone do nariz:Rot[Y]
2. Rolar o avião para a esquerda:-Rot[X]
3. Guia para a esquerda:Rot[Z]

Todo esse movimento seria representado como Rot[XYZ]. Tente mover o quadro um pouco você mesmo no RoboDK até se sentir confortável com esses conceitos.

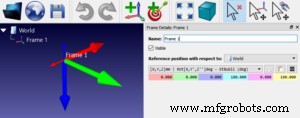
Em seguida, clique duas vezes no nome do quadro no canto superior esquerdo da janela principal para abrir o painel "Detalhes do quadro".

Uma orientação, várias rotações possíveis

Usando o RoboDK, tente as seguintes tarefas.

Antes de cada tarefa, redefina o quadro abrindo o ícone do menu “hambúrguer” (três linhas horizontais) no painel Detalhes do quadro e selecionando “Redefinir (definir identidade)”.

1. Selecione o menu suspenso na parte superior das coordenadas e escolha a rotação Stäubli (X->Y'->Z") em vez de Genérico.
2. Gire o quadro para que o azul (Z) aponte para baixo e o vermelho (X) aponte para trás (ou seja, ambos são invertidos de sua posição inicial e verde (Y) é o mesmo que a posição inicial), mas apenas faça girando em torno do eixo Y.
3. Reinicialize o quadro e mova-o para a mesma rotação novamente. No entanto, desta vez use apenas uma rotação Z e depois uma rotação X.
4. Reinicialize o quadro e mova-o para a mesma rotação novamente. No entanto, desta vez use apenas uma rotação X e depois uma rotação Z.

Como você pode ver, pode haver mais de uma maneira de obter a mesma orientação.

O primeiro método poderíamos chamá-lo de Rot[Y], pois inclui apenas uma rotação em torno do eixo Y. O segundo método poderíamos chamá-lo de Rot[Z, X'], pois inclui uma rotação em torno do eixo Z e uma rotação em torno do novo eixo X. A terceira chamaríamos Rot[X, Z']. O símbolo principal significa que a rotação acontece em relação ao último movimento em vez dos eixos estáticos.

Este é o conceito fundamental por trás dos ângulos de Euler. Você pode girar um quadro para a mesma orientação de várias maneiras alterando a sequência de eixos e rotações.

Diferentes fabricantes de robôs escolheram diferentes combinações de rotações. Por exemplo, Stäubli usa uma convenção XY’Z”, Adept usa uma convenção ZY’Z”, KUKA usa uma convenção ZY’X” e Fanuc &Motoman usa convenção XYZ. Por outro lado, a ABB usa Quaternion e a Universal Robots usa um vetor de orientação. Mas todas as convenções podem ser usadas para representar qualquer orientação no espaço.

Você encontrará mais informações na Documentação do RoboDK.

Teste diferentes convenções de robô

Espero que isso esteja começando a fazer sentido. No entanto, este é apenas o começo. Para realmente dominar as convenções de ângulos de Euler no RoboDK, acho útil brincar com o software seguindo este guia.

Você pode ver o efeito de suas rotações em números nas caixas azul claro, roxo e amarelo no painel "Detalhes do quadro".

Por padrão, a convenção Generic XYZ é escolhida para novos quadros de referência. Tente selecionar diferentes fabricantes de robôs no menu suspenso acima das caixas coloridas. Tente inserir valores numéricos nas caixas para ver seus efeitos no quadro de referência.

Para um tutorial aprofundado sobre ângulos de Euler, também posso recomendar esta página em Mecademic.