Método para medição de parâmetros de movimento em vários graus de liberdade com base em grades de difração de acoplamento cruzado de polidimetilsiloxano

Resumo

Este trabalho apresenta um método de medição de parâmetros de movimento com vários graus de liberdade baseado no uso de redes de difração de acoplamento cruzado que foram preparadas nas duas faces de um substrato de polidimetilsiloxano (PDMS) usando tecnologia de processamento de plasma de oxigênio. O feixe de laser que viaja pela grade óptica de acoplamento cruzado seria difratado em um arranjo de pontos bidimensional. O deslocamento e o tamanho da lacuna do arranjo de pontos eram funções do movimento da fonte de laser, conforme explicado pelo efeito de difração de Fraunhofer. Um dispositivo de carga acoplada (CCD) de 480 × 640 pixels foi usado para adquirir imagens do arranjo de pontos bidimensional em tempo real. Um algoritmo proposto foi então usado para obter os parâmetros de movimento. Usando este método e o CCD descrito acima, as resoluções do deslocamento e do ângulo de deflexão foram de 0,18 μm e 0,0075 rad, respectivamente. Além disso, um CCD com uma contagem de pixels mais alta pode melhorar as resoluções do deslocamento e do ângulo de deflexão para escalas sub-nanométricas e micro-radianas, respectivamente. Finalmente, as posições dinâmicas de aeronaves de asas rotativas pairando foram rastreadas e verificadas usando o método proposto, que pode ser usado para corrigir a posição da aeronave e fornecer um método para estabilização da aeronave no céu.

Histórico

Parâmetros de movimento com vários graus de liberdade podem fornecer informações precisas de localização e atitude sobre um alvo específico, que têm sido amplamente utilizados para grandes estruturas em aplicações como o controle de estabilidade de atitude de aeronaves, a estabilidade de mira de sistemas de sonda de arma, braço robótico movimento, o alinhamento de peças de precisão e posicionamento da peça para processamento industrial [1,2,3].

Portanto, métodos de detecção de alta precisão foram usados ​​para detectar informações de vários graus de liberdade (por exemplo, retidão, inclinação e ângulo de deflexão) sobre os alvos, e esses métodos exigiam sensores de alto desempenho, incluindo a característica de detecção de alta velocidade , sincronização, alta precisão de medição e em tempo real. Esses métodos foram amplamente usados ​​em aplicações aeroespaciais, veículos aéreos não tripulados, manufatura de precisão e alinhamento óptico [4,5,6].

O método de medição precisa em tempo real e desacoplamento das informações dinâmicas do movimento de vários graus de liberdade foram os elementos-chave para determinar a estabilidade da atitude da portadora. Hsieh [7] propôs uma matriz de detecção tridimensional que usava três grupos de módulos para detectar os diferentes graus de liberdade, em que diferentes módulos de detecção foram usados ​​para medir as diferentes informações de posição e um algoritmo foi usado para calcular a informações de graus de liberdade. Liu [8] apresentou um método de medição de parâmetros de movimento com vários graus de liberdade baseado na mudança no ângulo relativo entre duas grades de montagem para realizar as medições de informação. No entanto, a abordagem acima estava sujeita a erros de montagem de dois ou mais elementos sensores e a complexidade dos cálculos de acoplamento, e sua precisão também depende do sistema de instrumentos de alta precisão.

Com o desenvolvimento da tecnologia de fabricação de micro-nano, nanotecnologia e nanomateriais, os pesquisadores estudaram os métodos de detecção de parâmetros de movimento de vários graus de liberdade com base na implementação de um único chip, da perspectiva da miniaturização e aplicação de baixo custo no campos de nanomateriais, materiais ópticos e nanodispositivos. Tana [9] relatou um algoritmo de detecção de parâmetros de movimento com vários graus de liberdade com um feixe não difrator baseado em uma estrutura de prisma miniaturizado portátil, o que poderia minimizar os erros de medição. Nossa equipe apresentou um método de medidor de deformação vetorial baseado em um único elemento sensor que pode ser aplicado a medições de deformação vetorial de superfície usando sensores mecânicos integrados de múltiplos eixos e forneceu a base para a pesquisa neste artigo [8, 10].

Neste trabalho, um deslocamento vetorial de vários graus de liberdade e um método de medição de ângulo foram demonstrados com base em um único elemento; este elemento foi fabricado usando tecnologia de processamento de plasma de oxigênio para formar uma estrutura de grade óptica gradiente ortogonal em ambos os lados de um substrato de polidimetilsiloxano (PDMS) que foi pré-dobrado em forma de elipse. Essas grades ópticas cruzadas podem fazer com que um feixe de laser de entrada seja difratado em uma matriz de pontos bidimensional. As informações de localização do ponto de difração podem ser usadas para atingir o ângulo do feixe incidente calculado pelo algoritmo de localização em tempo real. Com base neste método e em um dispositivo de carga acoplada (CCD) de 480 × 640 pixels, as resoluções de medição do deslocamento e do ângulo de deflexão foram de 0,18 μm e 0,0075 rad, respectivamente. Além disso, pixels maiores CCD podem melhorar a resolução de medição do deslocamento e o ângulo de deflexão para níveis sub-nanométricos e micro-radianos, respectivamente. Finalmente, a posição dinâmica de uma aeronave de asas rotativas pairando foi rastreada usando o método proposto em tempo real; as informações adquiridas podem ser usadas para corrigir a posição da aeronave e prova um novo método para estabilização de aeronaves no céu.

Experimental

Preparação de polidimetilsiloxano (PDMS)

O PDMS (Sylgard 184) foi adquirido da Dow Corning. As membranas PDMS (10:1) foram preparadas por spin coating em wafers de silício e foram curadas imediatamente após a centrifugação a temperaturas inferiores a 80 ° C durante 2 h. Substratos de PDMS com espessura de 600 μm foram preparados controlando a velocidade de rotação.

Preparação da grade ortogonal dupla

De acordo com os requisitos experimentais, os filmes PDMS foram preparados com uma área de 3 × 3 cm ² . Os filmes PDMS foram então pré-tensionados em relação ao original 1,5 vezes na direção X usando um estágio de tradução caseiro. SiO enrugado _x camadas foram então formadas no O ₂ substrato PDMS pré-tensionado tratado com plasma (IoN Wave 10, PVA-TePla, Alemanha) sob condições de uma taxa de fluxo de oxigênio de 30 sccm e um tempo de oxidação de 40 s. Estruturas nanograting uniformes e ordenadas foram formadas na superfície do substrato PDMS depois de relaxado o pré-tensionado. Conforme mostrado na Fig. 1a, este processo foi repetido tomado do outro lado do substrato PDMS com uma diferença angular de 90 °, para formar as estruturas de grade ortogonal em ambos os lados do substrato PDMS.

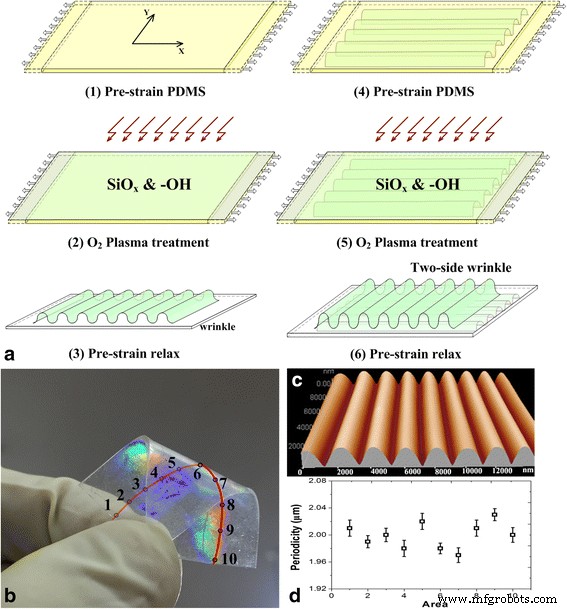
Processo de fabricação e caracterizações morfológicas de grades ópticas duplas de PDMS. a Fabricação de grade ótica dupla. b As imagens ópticas da grade. c Imagem de microscopia de força atômica da grade. d A uniformidade de periodicidade para as amostras

Criação da plataforma de teste

O sistema de sensor de ângulo de deslocamento de quatro graus de liberdade foi construído e inclui uma fonte de luz laser, um conjunto de plataforma de ângulo e deslocamento, um suporte de amostra, uma tela, uma câmera CCD e um computador. Conforme mostrado na Fig. 2a, a fonte de luz laser He-Ne (comprimento de onda do laser 680 nm) foi instalada no conjunto de plataforma de ângulo e deslocamento que consistia em uma plataforma giratória elétrica e uma estrutura de ajuste tridimensional manual (Beijing Zolix Instrument Co., Ltd .). A plataforma possui precisão rotacional de 0,1 ° e precisão de deslocamento de 2 μm. Esta grade óptica cruzada pode fazer com que o feixe de laser seja difratado em uma matriz de pontos bidimensional. Uma câmera semicondutora de óxido metálico complementar (CMOS) com 480 × 640 pixels foi usada para adquirir uma imagem da matriz de pontos bidimensionais em tempo real usando algoritmos de processamento de imagem MATLAB, que foi usado para extrair cada localização do ponto de difração e, em seguida, calcular o x- e y - deslocamentos do eixo e as informações do ângulo. Uma plataforma de teste na forma de uma aeronave de quatro rotores (Typhoon Q500, Yuneec Electric Aviation) foi fornecida. E informações de quatro graus de liberdade foram adquiridas para obter a atitude de pairar em ambientes fechados.

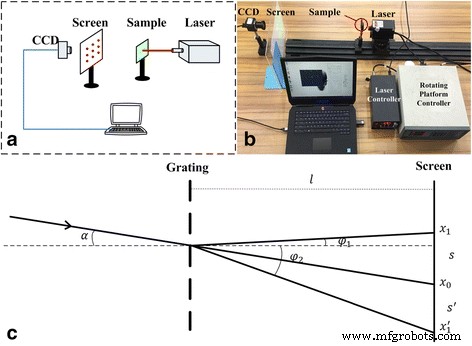
O princípio e o sistema de teste para o parâmetro de movimento MODF. a diagrama do sistema. b Configuração do sistema. c Princípio de teste de deslocamento e ângulo

Análise e discussão

Caracterização de grade de PDMS ortogonal

O processo de fabricação foi mostrado como na Fig. 1a. A modificação da superfície hidrofílica do PDMS usou a tecnologia de plasma de oxigênio. Um SiO _x camada e grupos hidrofílicos (por exemplo, −OH) foram, portanto, formados nos substratos PDMS pré-dobrados pelo plasma de oxigênio. Quando a pré-deformação no substrato do PDMS excede um valor crítico, estruturas de grade foram formadas na superfície do PDMS após o relaxamento da pré-deformação [11, 12]. A periodicidade das grades foi alcançada pelo ajuste das condições de pré-flexão e plasma aplicadas e pode ser calculada em nossos trabalhos anteriores. Conforme mostrado na Fig. 1c, as topografias das micro- / nanogratings foram caracterizadas por microscopia de força atômica (AFM) (CSPM5500; Benyuan Co.). Conforme mostrado na Fig. 1b, d, 10 áreas foram selecionadas ao longo da linha central em um lado da amostra para estudar a periodicidade e a uniformidade das estruturas de grade. A periodicidade correspondente de grades de 10 áreas foi uniforme e teve um período de (2 ± 0,05) μm em toda a superfície da amostra.

Grade de difração para caracterização de parâmetro de posição e ângulo de movimento

O feixe de laser viaja pela amostra (com a grade) para difratar na matriz de pontos de luz, de acordo com a teoria de difração de Fraunhofer [13]. A posição do ponto de difração estava diretamente relacionada à posição e ao ângulo do feixe incidente e, portanto, a informação de posição do feixe incidente pode ser detectada pela informação de localização dos pontos de difração.

A Figura 2 mostra a plataforma móvel e giratória para rastrear o posicionamento e os pontos de difração correspondentes do feixe incidente. De acordo com a teoria de difração de Fraunhofer, quando a rede de difração e a distância da tela são fixas, a relação entre o feixe incidente, o feixe difratado e o comprimento de onda pode ser expressa da seguinte forma:
$$ d \ left (\ sin \ varphi \ pm \ sin \ alpha \ right) =m \ lambda \ left (m =0,1,2, \ dots \ right) $$ (1)
Aqui, λ era o comprimento de onda do feixe incidente, d foi o período da grade, α foi o ângulo de incidência, φ era o ângulo de difração, e m foi a ordem de difração de grade.

Quando o ângulo de incidência α não era igual a 0, “+” indica então que o feixe de difração e o feixe incidente estão distribuídos no mesmo lado da normal de grade, enquanto “-” indica que o feixe de difração e o feixe incidente existem em dois lados da normal. Em um ângulo de incidência específico, as distâncias entre a primeira ordem dos pontos de difração e a ordem zero dos pontos de difração não eram iguais na tela. Portanto, a distância entre os pontos pode mudar com o ângulo de incidência. O ângulo do feixe incidente pode ser calculado quantitativamente através do cálculo da posição do ponto de luz de difração. Simultaneamente, a localização móvel do feixe incidente causa movimento da ordem zero do ponto de difração. A informação da posição do feixe incidente pode ser calculada pela informação de localização da ordem zero do ponto do feixe de difração.

A Figura 2c mostra uma única direção do diagrama de difração de grade, onde x ₀ era a primeira ordem de pontos de difração, e x ₁ e \ ({x} _1 ^ {\ hbox {'}} \) indicam a segunda ordem dos pontos de difração. Da Fig. 2c, s e s 'Eram a distância entre a primeira e a segunda ordem de pontos de difração que foram expressos da seguinte forma:
$$ s =l \ tan \ alpha + l \ tan {\ varphi} _1 $$ (2) $$ {s} ^ {\ hbox {'}} =l \ tan \ alpha -l \ tan {\ varphi} _2 $$ (3)
Da Eq. (1):
$$ d \ left (\ sin {\ varphi} _1 + \ sin \ alpha \ right) =\ lambda $$ (4) $$ d \ left (\ sin {\ varphi} _2- \ sin \ alpha \ right) =\ lambda $$ (5)
Do exposto, o modelo de correlação entre o ângulo de incidência do feixe e o espaçamento do ponto de difração pode ser obtido como:
$$ s =l \ tan \ alpha + \ tan \ left (\ arcsin \ left (\ frac {\ lambda} {d} - \ sin \ alpha \ right) \ right) $$ (6) $$ {s} ^ {\ hbox {'}} =l \ tan \ alpha - \ tan \ left (\ arcsin \ left (\ frac {\ lambda} {d} + \ sin \ alpha \ right) \ right) $$ (7)

Detecção e caracterização de parâmetros de movimento multi-graus de liberdade baseados em grade de difração ortogonal

O feixe de laser que viaja através de uma grade óptica de direção única pode formar os pontos de difração únicos. A orientação ortogonal pode ser formada à medida que o feixe de laser passa pelas grades ortogonais nos dois lados do substrato PDMS. Um feixe de difração de grade unidimensional será formado quando um feixe de luz é transmitido ao longo da direção da grade em um lado da tela e as dimensões foram definidas no x -eixo. Um feixe de difração de grade unidimensional foi então formado ortogonal ao x -eixo quando um feixe de luz passa ao longo da direção da grade no outro lado da tela e a dimensão é então definida no y -eixo. Uma matriz de pontos de difração bidimensional foi formada na tela, como mostrado na Fig. 3b.

O parâmetro de movimento MODF depende do movimento dos pontos de difração. a Pontos de difração unidimensionais foram gerados pela grade unidirecional. b A matriz de pontos bidimensionais foi gerada pela grade óptica cruzada dupla. c O movimento da matriz de pontos foi controlado pelo movimento da fonte de laser. d O espaço em movimento entre a matriz de pontos foi controlado como o ângulo de incidência do feixe de laser

Quando a posição de um feixe de laser foi alterada, a ordem zero da posição do ponto de luz de difração mostrará um movimento correspondente, e a posição do bitmap de difração mudará de acordo com a teoria de difração de Fraunhofer. A posição do feixe incidente pode ser calculada diretamente com base na direção do movimento da rede e, em seguida, detectada a informação de posição percebida do feixe de luz ao longo do x- e y -eixo. Como mostrado na Fig. 3c, a primeira ordem da posição do ponto de difração não pode calcular com precisão o deslocamento da luz devido aos efeitos de acoplamento do deslocamento e da deflexão. Além disso, a ordem zero da localização do ponto de difração estava relacionada apenas à localização da fonte. Portanto, seria mais preciso usar a ordem zero do deslocamento do ponto de difração para calcular a posição da fonte de luz. Conforme mostrado na Fig. 3d, as informações do ângulo de deflexão dos feixes de luz incidentes ao longo do x -eixo e o y -eixo pode ser calculado pela distância entre o ponto de luz no x -eixo e o y -eixo baseado no modelo relacionado entre o ângulo e a mudança do ponto.

No entanto, a limitação do motivo do deslocamento dos pontos de difração depende do ângulo de incidência e da distância entre a grade e a tela com base na Eq. (1). Em nossos trabalhos, a grade foi fixada com a tela, o que significa que a variação da distância entre a grade e a tela foi zero. Não houve deslocamento de pontos de difração quando a fonte de laser estava se movendo ao longo do z -eixo. Também, quando a fonte de laser estava girando ao longo do z -eixo, a variação do ângulo de incidência foi zero, o que resultaria no não deslocamento dos pontos de difração.

Em nossos experimentos, o ângulo muda (Δ θ _x ) ao longo do x -eixo pode ser calculado em termos de espaçamentos de coluna ( s _x , \ ({s} _x ^ {\ hbox {'}} \)) dos pontos de difração, e a mudança do ângulo (∆ θ _y ) ao longo do y -eixo pode ser calculado com base nos espaçamentos das colunas ( s _y , \ ({s} _y ^ {\ prime} \)) dos pontos de difração. A plataforma do portfólio foi ajustada para alterar a localização da fonte de luz e, em seguida, as imagens da câmera foram adquiridas pelo software MATLAB a cada 0,02 s para extrair a posição dos pontos de difração para comparação com os valores anteriores, que foram usados ​​para calcular os deslocamentos da matriz de pontos no x -eixo e o y -eixo e as alterações no espaçamento de coluna e espaçamento de linha da matriz.

Com base no algoritmo, o deslocamento da matriz de pontos pode ser analisado manipulando a imagem antes e depois do movimento para calcular o ∆ x , ∆ y , ∆ θ _x , e ∆ θ _y . Como o ponto de laser inclui vários pixels na imagem e sua energia está de acordo com a distribuição gaussiana, o método de ajuste de distribuição gaussiana foi usado para remover o ruído de fundo da imagem para extrair a localização do centro do ponto de laser com precisão. A função gaussiana do ponto de laser é expressa da seguinte forma:
$$ I \ left (x, y \ right) =H \ cdot \ exp \ left \ {- \ left [\ frac {{\ left (x \ hbox {-} xo \ right)} ^ 2} {\ sigma_1 ^ 2} + \ frac {{\ left (y \ hbox {-} yo \ right)} ^ 2} {\ sigma_2 ^ 2} \ right] \ right \} $$ (8)
Aqui, eu ( x , y ) foi a intensidade do local e H era a amplitude, ( x ₀ , y ₀ ) eram as coordenadas do centro do ponto de luz e σ ₁ , σ ₂ foram os desvios padrão no x -eixo e o y -eixo, respectivamente.

Um logaritmo pode ser aplicado a ambos os lados da equação acima para obter a localização do centro do ponto, que pode ser expresso da seguinte forma:
$$ {x} _0 =- \ frac {c} {2a} $$ (9) $$ {y} _0 =- \ frac {d} {2b} $$ (10)
Aqui, a , b , c e d foram os coeficientes polinomiais que foram obtidos pelo ajuste gaussiano de todos os pixels no local.

As mudanças de distância entre dois pontos de difração foram calculadas por duas imagens antes e depois do movimento. E o ponto central dos pontos de difração foi definido como o sistema de centros de coordenadas antes do movimento:o deslocamento absoluto e os sistemas de coordenadas de deslocamento relativo do ponto de luz. O sistema de coordenadas de deslocamento absoluto do ponto de luz de difração tomou uma tela de quietude como referência. As informações de movimento ( Δx , Δy ) da rede em ambas as telas pode ser calculada pela ordem zero da coordenada do ponto de difração (isto é, a posição central). O sistema de coordenadas de deslocamento relativo para o ponto de luz tomou a ordem zero do ponto de difração como referência, que pode ser usado para calcular as mudanças no espaçamento da matriz de pontos ( S _x ) e o espaçamento entre linhas ( S _y )

A Figura 4 mostra a caracterização dos quatro graus de liberdade. Quando o feixe de laser estava cortando ao longo do x -eixo, houve um movimento correspondente da rede de difração no x -eixo, mas o deslocamento foi cerca de zero no y -eixo. A sensibilidade de deslocamento foi de cerca de 5,4 pixels / μm. Este método pode ser usado para calcular a informação de localização para a fonte de luz ao longo do eixo com alta precisão, como mostrado na Fig. 4a.

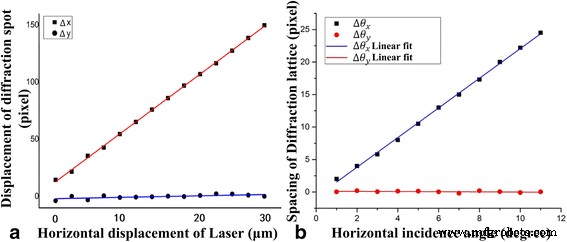
Caracterização de quatro graus de liberdade. a O deslocamento da fonte do laser depende do deslocamento dos pontos de difração. b O ângulo de incidência da fonte de laser depende da lacuna entre os pontos de difração

Quando o laser girou um pequeno ângulo ao longo do x -eixo, havia uma mudança de distância correspondente de espaçamento de linha de arranjo de pontos de difração e o espaçamento de coluna de arranjo de pontos era zero. A sensibilidade de deslocamento foi de cerca de 2,3 pixels por ângulo (/ °). Enquanto isso, a faixa de medição do ângulo era de cerca de 9,8 ° em teoria calculada pelas Eqs. (1) - (5) como a distância s =0. Atribuindo a primeira ordem dos pontos de difração coincide com a ordem zero dos pontos de difração conforme aumenta o ângulo de incidência, a mudança de distância dos pontos de difração seria zero ( s =0). Este método pode ser usado para obter a informação do ângulo da fonte de luz ao longo do x -eixo. As informações de localização e ângulo também podem ser obtidas usando este método.

A resolução de detecção de um pixel depende do algoritmo baseado no software MATLAB. Conforme calculado acima, o método tem uma sensibilidade de deslocamento de 5,4 pixels / μm, o que significa que a resolução foi de 0,18 μm . Para a sensibilidade de deslocamento de 2,3 pixels / ° , era uma resolução de 0,0075 rad. Isso mostra que, com base no método aqui apresentado e na resolução do CCD, as resoluções do deslocamento e do ângulo foram de 0,18 μm e 0,0075 rad, respectivamente. O CCD de 480 × 640 pixels foi usado para adquirir a imagem da matriz de pontos bidimensional em tempo real. Além disso, pixels maiores CCD e otimização do caminho da luz podem melhorar as resoluções do deslocamento e do ângulo de deflexão em escalas sub-nanométricas e micro-radianas, respectivamente.

Caracterização das informações dos parâmetros de movimento do rotor da aeronave pairando

Uma aeronave de asas rotativas era um tipo de sistema de aeronave civil não tripulada com baixa precisão, amplamente utilizado em aeronaves, modelos de aeronaves e navegação. O controle de estabilidade de um helicóptero representa um microcosmo de uma plataforma de combate não tripulada. Para realizar o controle de vôo de alta precisão, o aspecto mais importante era o controle constante da atitude e posição da aeronave. E o aspecto central foi a decodificação da atitude de pairar de alta precisão e das informações de posição em tempo real, de modo que as informações precisas dos parâmetros de movimento de quatro graus de liberdade sobre o pairar se tornassem um recurso essencial.

Em nosso experimento, baseado em uma rede de difração de acoplamento cruzado, um método de medição foi apresentado para obter as informações de atitude de quatro graus de liberdade do vôo da aeronave em tempo real. Primeiro, uma aeronave de quatro rotores foi usada para substituir a plataforma, que era composta pela posição e postura de um sistema de teste de quatro graus de liberdade, que se baseava em uma grade dupla para configurar os quatro graus de liberdade - sistema de teste de atitude de liberdade para aeronaves de quatro rotores. No sistema de teste, um pequeno apontador laser foi fixado no centro de uma aeronave de quatro rotores como fonte de luz e ilumina os feixes de laser verticalmente para baixo. Uma amostra com grade dupla, uma tela e uma câmera giram ao longo do centro do eixo óptico. Esta grade óptica cruzada pode fazer com que o feixe de laser seja difratado em uma matriz de pontos bidimensional. Nos experimentos, a câmera foi utilizada para adquirir a imagem da tela e transmitir as imagens ao computador em tempo real para calcular as informações de deslocamento pelo software MATLAB.

Para obter medições rápidas, precisas e em tempo real dos sinais de vôo, uma aeronave de quatro rotores estava pairando no ar e rastreando rapidamente o sinal de postura mantido por 4 s. Informações sobre os deslocamentos axiais ao longo do x -eixo e o y - os eixos para aeronaves de quatro rotores foram obtidos no tempo de 4 s, conforme mostrado na Fig. 5c. Com base no estabelecimento de um sistema de coordenadas planas (ou seja, um x -eixo e um y -eixo), o x e y os valores são convertidos nesses pontos de coordenada. O posicionamento 200 resulta em 4 s significa um ponto adquirido em 0,02 s. Isso representa o uso do método de rastreamento da aeronave a cada 0,02 s em tempo real para determinar sua localização e posição. A aeronave tem um deslocamento máximo de 2,1 mm no x -eixo e deslocamento máximo de 2,3 mm no y -eixo, de acordo com o algoritmo.

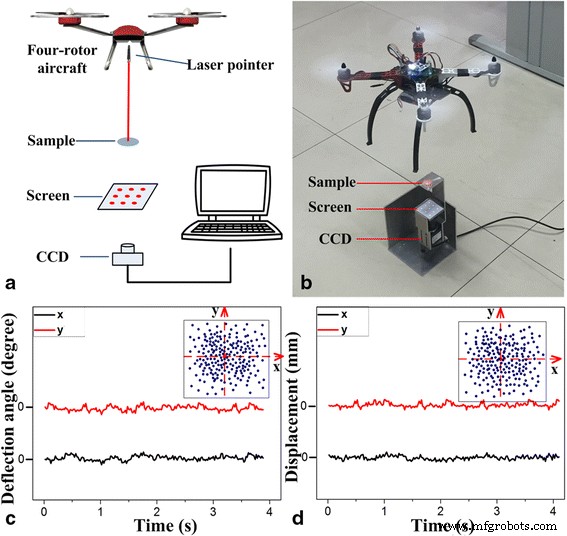
Caracterizações da atitude de naves com quatro rotores. a Diagrama do sistema. b Configuração do sistema. c Ângulo de deflexão da embarcação com rotor. d Deslocamento da nave do rotor

Além disso, as informações de ângulo de inclinação e ângulo de rotação para a aeronave foram calculadas pelo algoritmo acima e método de processamento de dados. Conforme mostrado na inserção da Fig. 5d, o diagrama de pontos do ângulo de rotação da aeronave de quatro rotores entregou informações de ângulo precisas para aeronaves rastreando em tempo real a cada 0,02 s. Observou-se que a aeronave possui um desvio angular máximo de 1 ° no x -eixo e o y- eixo. Este método pode, assim, calcular a informação de quatro graus de liberdade para a aeronave, que pode realimentar os sinais precisos de posição e ângulo para o sistema de controle de vôo em 0,02 s para melhorar a estabilidade da aeronave.

Conclusões

Em resumo, uma tecnologia simples de fabricação foi demonstrada para fabricar a estrutura de grade óptica ortogonal com periodicidade de 2 μm nos dois lados do substrato PDMS. Com base na estrutura de grade óptica ortogonal, um método foi estudado para identificar a posição do feixe e uma informação de parâmetro de movimento angular usando a informação de posição do ponto de luz de difração com base no efeito de difração de Fraunhofer. Um CCD de 480 × 640 pixels foi usado para adquirir imagens da matriz de pontos bidimensional em tempo real. Os resultados mostram que, ao utilizar este método e o CCD descrito acima, as resoluções do deslocamento e do ângulo de deflexão foram de 0,18 μm e 0,0075 rad, respectivamente. Além disso, com o CCD de pixel mais alto, as resoluções do deslocamento e do ângulo de deflexão podem melhorar em escalas sub-nanométricas e micro-radianas, respectivamente. Este método pode ser usado para detectar posições de pairar precisas e informações de ângulo para aeronaves com rotor em tempo real com alta precisão a cada 0,02 s. A informação pode dar a volta ao controle do sistema de vôo para veículos aéreos não tripulados no ar. Este método era simples, de baixo custo e alta precisão e pode realizar monitoramento em tempo real enquanto fornece uma base de pesquisa para vôo estável e controle preciso de aeronaves para plataformas de combate não tripuladas.

Síntese e propriedades eletroquímicas de materiais catódicos de LiNi0,5Mn1,5O4 com dopagem composta Cr3 + e F− para baterias de íon-lítio Estudo de primeiros princípios sobre a estabilidade e imagem STM de Borophene