Propriedades das oscilações eletromagnéticas longitudinais em metais e sua excitação em superfícies planas e esféricas

Resumo

A definição comum de permissividade espacialmente dispersiva é revisada. A resposta do gás de elétron degenerado em um campo elétrico satisfazendo a equação vetorial de Helmholtz é encontrada com uma solução para a equação de Boltzmann. A função dielétrica longitudinal calculada coincide com a obtida por Klimontovich e Silin em 1952 e Lindhard em 1954. Porém, depende do quadrado do número de onda, um parâmetro da equação vetorial de Helmholtz, mas não do vetor de onda de uma onda eletromagnética plana. Este novo conceito simplifica a simulação dos efeitos não locais, por exemplo, com uma teoria de Lorents-Mie generalizada, uma vez que nenhuma transformação de Fourier deve ser feita. Os coeficientes de Fresnel são generalizados permitindo a excitação das ondas eletromagnéticas longitudinais. Para verificar a teoria, os espectros de extinção para esferas nanométricas de prata e ouro são calculados. Para essas partículas, a teoria generalizada de Lorents-Mie fornece o deslocamento para o azul e o alargamento da ressonância do plasmon que estão em excelente acordo com os dados experimentais. Além disso, a teoria não local explica o desaparecimento da ressonância plasmônica observada para esferas de ouro com diâmetros menores ou iguais a 2 nm. Os cálculos usando as funções dielétricas de Klimontovich-Silin-Lindhard e hidrodinâmica para prata dão resultados próximos em energias de fótons de 3 a 4 eV. Mostramos que os valores absolutos dos números de onda das ondas longitudinais nos sólidos são muito maiores do que os das ondas transversais.

Histórico

A irradiação de uma superfície plana de metal por pulsos de laser de femtossegundos freqüentemente resulta na formação de estruturas de superfície periódicas induzidas por laser (LIPSSs) [1]. Além do LIPSS, ondulações hiperfinas chamadas LIPSS de alta frequência espacial (HSFL) foram observadas [1, 2]. Os períodos espaciais do HSFL são significativamente menores do que o comprimento de onda de irradiação λ ₀ . Por exemplo, para o alumínio, este período foi estimado na faixa de 20 a 200 nm em λ ₀ =0,8 μ m [2,3]. Enquanto a orientação das ondulações no LIPSS comum era perpendicular à polarização da luz do laser, a orientação do HSFL era frequentemente perpendicular e às vezes paralela à polarização. HSFL semelhantes foram formados nas superfícies de dielétricos transparentes, semicondutores e metais. A origem do HSFL foi explicada por diferentes mecanismos, como geração de segundo harmônico, o envolvimento de tipos específicos de modos de plasmon, auto-organização e aprimoramentos de campo local durante a quebra não homogênea em materiais dielétricos [2, 3].

O objetivo deste estudo é pesquisar um processo de onda que poderia produzir um padrão com um curto período Λ ≪ λ ₀ . Nós examinamos as propriedades das ondas eletromagnéticas longitudinais (L) em metais, também conhecidas como ondas de plasma. Nosso estudo consiste nas seguintes novas etapas. Primeiramente, iniciamos nossa pesquisa com a definição da dispersão espacial da permissividade. Conforme mostrado abaixo, a definição comum é inútil se um meio em estudo não for uniforme e infinito. Portanto, propomos um novo conceito de função dielétrica espacialmente dispersiva ε . Esta função estabelece a proporcionalidade direta entre dois campos de vetor, E ( r , ω ) e D ( r , ω ), mas não as amplitudes E ( k , ω ) e D ( k , ω ) de ondas planas. Consequentemente, a quantidade ε depende do quadrado do número da onda, k ² , o parâmetro do vetor da equação de Helmholtz para o campo elétrico E ( r , ω ), mas não o vetor de onda k das ondas planas. Então, para derivar essa nova função, determinamos a resposta dos elétrons de condução em um modo eletromagnético resolvendo a equação de transporte de Boltzmann escrita na aproximação do tempo de relaxação. As chamadas funções dielétricas transversais e longitudinais de Lindhard foram obtidas. Além disso, descobrimos que o Lindhard longitudinal e a função hidrodinâmica muito mais simples estão próximos em uma ampla gama de parâmetros. A extinção da luz por nanoesferas de prata e ouro foi considerada para ilustrar a teoria. Mostramos pela primeira vez que a teoria de Mie não local explica o deslocamento para o azul, alargamento e eventual desaparecimento das ressonâncias plasmônicas observadas com uma diminuição do tamanho das nanoesferas de metal nobre. Finalmente, o modelo teórico desenvolvido recentemente foi aplicado para examinar a possibilidade de envolvimento dos modos longitudinais na formação das estruturas superficiais induzidas por laser. Para tanto, modificamos a teoria de Fresnel levando em consideração as ondas longitudinais transmitidas.

Métodos

Para determinar os campos eletromagnéticos em meios homogêneos por partes, a teoria eletromagnética clássica foi aplicada. O campo elétrico E em cada domínio uniforme do meio heterogêneo foi assumido como uma solução da equação vetorial de Helmholtz (VHE):
$$ \ Delta \, \ mathbf {E} + k ^ {2} \, \ mathbf {E} =0, $$ (1)
onde Δ é a operadora Laplace.

Como de costume, os componentes tangenciais do elétrico E e magnético H os campos são contínuos além das fronteiras da mídia. Além disso, levamos em consideração que os elétrons estão confinados no metal; portanto, a seguinte condição de contorno adicional (ABC) para o componente normal da densidade de corrente j na superfície do metal S foi usado:( j n ) | _{r ∈ S} =0.

Para determinar a corrente de condução no metal, resolvemos a equação de transporte de Boltzmann (BTE) escrita na aproximação do tempo de relaxação:
$$ \ frac {\ partial f} {\ partial t} + \ mathbf {v} \, \ frac {\ partial f} {\ partial \ mathbf {r}} + \ frac {e} {m} \, \ esquerda (\ mathbf {E} + \ mathbf {v} \ times \ mathbf {B} \ direita) \, \ frac {\ partial f} {\ partial \ mathbf {v}} =\ frac {f_ {0} - f} {\ tau}, $$ (2)
onde f é a função de distribuição de partícula única no espaço de fase ( r , v ), v é a velocidade microscópica do elétron, e e m são a carga e a massa do elétron, respectivamente, B é a indução magnética, f ₀ é uma função de distribuição de equilíbrio, e τ é o momento de relaxamento.

Abaixo, derivamos fórmulas para as funções dielétricas espacialmente dispersivas. Então, nós os usamos para estudar a reflexão da luz de uma superfície plana de metal e o espalhamento da luz em uma nanosfera de metal nobre.

Resultados e discussão

Dispersão espacial de ε em um meio heterogêneo

Na literatura, uma função dielétrica espacialmente dispersiva ε é definido através da seguinte relação [4-6]:
$$ \ mathbf {D} (\ omega, \, \ mathbf {r}) =\ epsilon_ {0} \ iiint \ limits _ {- \ infty} ^ {\ infty} \! \ mathbf {d} \ mathbf {r} ^ {\ prime} \, \ epsilon \ left (\ omega, \, \ mathbf {r} - \ mathbf {r} ^ {\ prime} \ right) \, \ mathbf {E} \ left (\ omega, \, \ mathbf {r} ^ {\ prime} \ right), $$ (3)
onde ε ₀ é a constante elétrica, D ( ω , r ) é a amplitude da oscilação do vetor de deslocamento com frequência angular ω no ponto r , e E ( ω , r ^′ ) a amplitude da oscilação do campo elétrico no ponto r ^′ . Transformadas de Fourier da Eq. (3) dê a equação
$$ \ mathbf {D} (\ omega, \, \ mathbf {k}) =\ epsilon_ {0} \, \ epsilon (\ omega, \, \ mathbf {k}) \, \ mathbf {E} (\ ômega, \, \ mathbf {k}) $$ (4)
onde um espacialmente dispersivo ε ( ω , k ) depende do vetor de onda k de uma onda eletromagnética plana. Em nossa opinião, a Eq. (3) não é ambíguo apenas em um volume homogêneo infinito, mas lidamos com um sistema heterogêneo por partes onde os limites devem ser levados em consideração e k não são os mesmos em mídias diferentes.

Nossa abordagem não usa a expansão das ondas eletromagnéticas sobre ondas planas. A permissividade espacialmente dispersiva determina a relação entre D ( ω , r ) e uma solução particular para o vetor Helmholtz Eq. (1):
$$ \ mathbf {D} (\ omega, \, \ mathbf {r}) =\ epsilon_ {0} \, \ epsilon (\ omega, \, k) \, \ mathbf {E} (\ omega, \, \ mathbf {r}). $$ (5)
Aqui E ( ω , r ) denota a distribuição do campo elétrico, mas não apenas o vetor E no ponto r .

Funções Dielétricas Longitudinais e Transversais

A permissividade dos metais é comumente expressa através da condutividade σ [4]:
$$ \ epsilon =\ epsilon _ {\ mathrm {g}} + \ frac {i \, \ sigma} {\ omega \, \ epsilon_ {0}}, $$ (6)
onde ε _g é uma parte da função dielétrica permitindo a polarização do sólido; ε _g =1 para um metal simples. Para determinar σ , calculamos a densidade atual
$$ \ mathbf {j} =e \ iiint \ limits _ {- \ infty} ^ {\ infty} \! \ mathbf {v} \, f \, \ mathrm {d} \ / \ mathbf {v} =\ sigma \, \ mathbf {E}, $$ (7)
onde \ (\ mathrm {d} \ mathbf {v} =\ frac {v} {m} \, \ mathrm {d} \ epsilon \, \ mathrm {d} \, \ Omega, \) d Ω =sin θ d θ d ϕ , v , θ , ϕ são as coordenadas esféricas da velocidade. Ao contrário de pesquisas anteriores, não introduzimos o vetor de onda k mas encontrou uma solução BTE na forma de uma série infinita contendo operadores v ∇ agindo em v E :
$$ f =f_ {0} + \ frac {e} {- i \ omega + \ Gamma} \, \ frac {\ partial f_ {0}} {\ partial \ epsilon} \ left [1+ \ frac {\ mathbf {v} \, {\ mathbf {\ nabla}}} {- i \ omega + \ Gamma} \ right] ^ {- \, 1} \! \ mathbf {v} \, \ mathbf {E}, $$ (8)
onde Γ =1 / τ . Então, f ₀ foi aproximado por uma distribuição Fermi-Dirac de temperatura zero e, após integração sobre ε na Eq. (7), nós temos
$$ \ mathbf {j} =\ frac {\ omega _ {\ mathrm {p}} ^ {2} \, \ varepsilon_ {0}} {- i \ omega + \ Gamma} \, \ frac {3} {4 \ pi} \ iint \ mathbf {u} \, \ left (1+ l \, \ mathbf {u} \ mathbf {\ nabla} \ right) ^ {- \, 1} (\ mathbf {u} \, \ mathbf {E}) \, \ mathrm {d} \, \ Omega, $$ (9)
onde \ (\ omega _ {\ mathrm {p}} ^ {2} =\ frac {e ^ {2} \, n_ {e}} {m \, \ varepsilon _ {0}}, \) ω _p é a frequência do plasma, \ (\ mathbf {u} =\ frac {\ mathbf {v}} {v} \) é o vetor unitário na direção de v , \ (l =\ frac {v _ {\ mathrm {F}}} {- i \ omega + \ Gamma}, \) v _F é a velocidade de Fermi. Além disso, calculamos as integrais
$$ \ begin {array} {* {20} l} &\ textstyle \ iint \ mathbf {u} \, (\ mathbf {u} \, \ mathbf {E}) \, \ mathbf {d} \, \ Omega =\ frac {4 \ / \ pi} {3} \, \ mathbf {E} \ end {array} $$ (10) $$ \ begin {array} {* {20} l} &\ textstyle \ iint \ mathbf {u} \, (\ mathbf {u} \, \ mathbf {\ nabla}) ^ {2 n-1} (\ mathbf {u} \, \ mathbf {E}) \, \ mathbf {d} \, \ Omega =0 \ end {array} $$ (11) $$ \ begin {array} {* {20} l} &\ textstyle \ iint \ mathbf {u} \, (\ mathbf {u} \, \ mathbf {\ nabla}) ^ {2 n} (\ mathbf {u} \, \ mathbf {E}) \, \ mathbf {d} \, \ Omega =\ frac {4 \ pi} {2 n + 3 } \\ &\ times \, \ Delta ^ {n-1} \ left [\ mathbf {\ nabla} \, (\ mathbf {\ nabla} \ cdot \ mathbf {E}) - \ frac {1} {2 n + 1} \, \ mathbf {\ nabla} \ times \ mathbf {\ nabla} \ times \ mathbf {E} \ right] \ end {array} $$ (12)
onde n é um número natural. A seguinte dependência de j em um arbitrário campo elétrico E foi finalmente obtido
$$ \ begin {array} {* {20} l} \ mathbf {j} &=\ frac {\ omega _ {\ mathrm {p}} ^ {2} \, \ varepsilon_ {0}} {- i \ omega + \ Gamma} \ left \ {\ mathbf {E} + 3 \, \ sum \ limits_ {n =1} ^ {\ infty} l ^ {\, 2 n} \ right. \\ &\ quad \ left. \ times \ frac {\ Delta ^ {n-1}} {2 n + 3} \ left [\ mathbf {\ nabla} \, (\ mathbf {\ nabla} \ cdot \ mathbf {E}) - \ frac {\ mathbf {\ nabla} \ times \ mathbf {\ nabla} \ times \ mathbf {E}} {2 n + 1} \ right] \ right \}. \ end {array} $$ (13)
Existem dois tipos de soluções para a Eq. (1), livre de divergência que satisfaz a equação ∇ · E =0 e sem rotação que satisfazem a equação
$$ \ mathbf {\ nabla} \ times \ mathbf {E} =0. $$ (14)
Para uma onda plana, com E ∝ exp [ i ( k r - ω t )], Eq. (14) se transforma na relação k × E =0 que mostra que a onda é longitudinal (L). Para simular processos em corpos esféricos, é conveniente usar o vetor de harmônicos esféricos L , M e N como um conjunto completo de funções ortogonais. Nesse caso, a Eq. (14) especifica harmônicos L . O número de onda das ondas L e L modos é determinado pela seguinte lei de dispersão
$$ \ epsilon ^ {\ mathrm {L}} \ left (\ omega, \, k ^ {\ mathrm {L}} \ right) =0. $$ (15)
Das Eqs. (6) e (13) encontramos que as soluções para a Eq. (1) satisfazendo a restrição da Eq. (14) dar a seguinte permissividade longitudinal
$$ \ epsilon ^ {\ mathrm {L}} =\ epsilon _ {\ mathrm {g}} - \ frac {\ omega _ {\ mathrm {p}} ^ {2}} {\ omega \, (\ omega + i \ Gamma)} \, \ frac {3} {2} \, \ Phi \ left (a ^ {2}, \, 1, \, \ frac {3} {2} \ right) $$ (16)
onde Φ é a função Phi de Lerch,
$$ \ frac {3} {2} \, \ Phi \ left (a ^ {2}, \, 1, \, \ frac {3} {2} \ right) =\ sum \ limits_ {n =0} ^ {\ infty} \ frac {3} {2 n + 3} \, a ^ {2 \, n}, $$ (17)
\ (a =\ frac {k v _ {\ mathrm {F}}} {\ omega + i \ Gamma} \).

A permissividade obtida difere daquela definida por Kliewer e Fuchs [7] apenas na notação:
$$ \ epsilon ^ {\ mathrm {L}} =\ epsilon _ {\ mathrm {g}} + \ frac {\ omega _ {\ mathrm {p}} ^ {2}} {\ omega \, (\ omega + i \ Gamma)} \, \ frac {3} {a ^ {2}} \ left [1- \ frac {1} {ia} \ tan ^ {- 1} (ia) \ right] $$ (18)
A identidade
$$ \ frac {1} {i a} \ tan ^ {- 1} (i a) =\ frac {1} {2} \ ln \ frac {1 + a} {1-a} $$ (19)
permite reescrever a Eq. (18) como segue
$$ \ epsilon ^ {\ mathrm {L}} =\ epsilon _ {\ mathrm {g}} - \ frac {\ omega _ {\ mathrm {p}} ^ {2}} {\ omega \, (\ omega + i \ Gamma)} \, \ frac {3} {a ^ {2}} \ left [1- \ frac {1} {2 a} \, \ frac {\ ln (1 + a)} {\ ln (1 -a)} \ right]. $$ (20)
No caso de Γ =0, esta fórmula assume a forma de uma equação derivada por Klimontovich e Silin [8] que estudaram o despejo de Landau em plasma degenerado (ver [9], [10, Eq. (40.17)] e [11]). A permissividade das Eqs equivalentes. (16), (18) e (20) é comumente chamada de função dielétrica de Lindhard (com referência a [12]), embora essa função tenha sido obtida pela primeira vez por Klimontovich e Silin [8].

A permissividade transversal de Lindhard [7] pode ser encontrada na Eq. (13) quando ∇ · E =0. No caso real de v _F k ≪ ω , se reduz à função dielétrica Drude
$$ \ epsilon ^ {\ mathrm {T}} =\ epsilon _ {\ mathrm {g}} - \ frac {\ omega _ {\ mathrm {p}} ^ {2}} {\ omega ^ {2} + i \ , \ Gamma \ / \ omega}. $$ (21)
Esta função concorda com dados experimentais em muitos metais [13]. Se | a | <1, a permissividade longitudinal (16) simplifica para a função dielétrica hidrodinâmica:
$$ \ epsilon ^ {\ mathrm {L}} \ left (\ omega, \, k ^ {\ mathrm {L}} \ right) =\ epsilon _ {\ mathrm {g}} - \ frac {\ omega _ {\ mathrm {p}} ^ {2}} {\ omega ^ {2} + i \, \ Gamma \ omega- \ frac {3} {5} \, \ left (v _ {\ mathrm {F}} \, k ^ {\ mathrm {L}} \ right) ^ {2}}. $$ (22)

Reflexão de uma onda eletromagnética plana a partir de uma superfície plana de metal

Condições de limite

Nesta seção, determinamos a direção do vetor de onda k ^L e amplitude da onda L excitada no metal durante a reflexão de uma onda eletromagnética plana de uma superfície plana de metal.

Considere um incidente de onda plana na interface dielétrico-metal z =0 com o vetor de onda no xz avião. O campo elétrico no meio dielétrico 1 consiste no incidente E _i e refletiu E _r ondas, o campo em metal 2 tem o transversal transmitido E _t e, em alguns casos, E longitudinal ^L componentes. De acordo com as condições de contorno de Maxwell, os componentes transversais dos vetores do campo elétrico e magnético são contínuos no plano z =0. Além disso, os elétrons não são ejetados do metal; portanto, o componente normal da densidade de corrente elétrica é zero em z =0,
$$ \ hat {\ mathbf {z}} \, \ mathbf {j} | _ {z =0} =0. $$ (23)
onde \ (\ hat {\ mathbf {z}} \) é o vetor unitário na direção de z eixo.

Todos os termos nas condições de contorno de Maxwell devem ter a mesma dependência de x e y . Esse requisito tem várias consequências. Em primeiro lugar, pode-se estabelecer que as ondas L podem ser excitadas apenas no caso de p-polarização quando o vetor elétrico da onda incidente E ^{( i )} é paralelo ao plano de incidência. Em outras palavras, os polaritons do plasmon podem ser gerados por uma onda magnética transversal (TM). O efeito é quase o mesmo que em uma esfera de metal [14]. Em segundo lugar, fórmulas semelhantes à lei de Snell podem ser derivadas das condições
$$ k_ {1x} =k_ {2x} =k_ {2x} ^ {\ mathrm {L}} =k_ {1} \, \ sin \ theta_ {1} $$ (24)
onde índices 1 x e 2 x denotam o x -projeções dos vetores na mídia 1 e 2, respectivamente, θ ₁ é o ângulo de incidência.

Coeficientes de reflexão e transmissão

Vamos determinar o campo formado por uma onda eletromagnética p-polarizada plana incidente em uma superfície plana de metal. É conveniente expressar os componentes dos campos elétricos e magnéticos através do x componente de E ^{( i )} , a saber E x (r) =- r E x (i) para a onda refletida, E x (t) = t E x (i) para a onda transversal transmitida, e
$$ E ^ {\ mathrm {(a)}} _ {x} =\ delta \, E ^ {\ mathrm {(t)}} _ {x} =t _ {\ mathrm {L}} \, E ^ {\ mathrm {(i)}} _ {x} $$ (25)
para a onda longitudinal transmitida, aqui r é um coeficiente de reflexão, t e t _L são coeficientes de transmissão.

A partir das condições de contorno de Maxwell e ABC da Eq. (23) escrito da seguinte forma
$$ \ hat {\ mathbf {z}} \, (\ mathbf {D} - \ epsilon_ {0} \ epsilon _ {\ mathrm {g}} \, \ mathbf {E}) | _ {z =0} =0, $$ (26)
obtemos
$$ \ begin {array} {* {20} l} r &=- \ frac {(1+ \ delta) \, \ epsilon_ {1} \, k_ {2z} - \ epsilon_ {2} \, k_ {1z }} {(1+ \ delta) \, \ epsilon_ {1} \, k_ {2z} + \ epsilon_ {2} \, k_ {1z}} =1- (1+ \ delta) \, t \ end { matriz} $$ (27) $$ \ begin {array} {* {20} l} t &=\ frac {2 \, \ epsilon_ {1} \, k_ {2z}} {\ epsilon_ {2} \, k_ {1z} + (1+ \ delta) \, \ epsilon_ {1} \, k_ {2z}}, \ end {array} $$ (28) $$ \ begin {array} {* {20} l} \ delta &=\ frac {\ epsilon _ {\ mathrm {g}} - \ epsilon} {\ epsilon _ {\ mathrm {g}}} \, \ frac {k_ {2x} ^ {2}} {k_ {2z} \, k_ {2z} ^ {\ mathrm {L}}} \ end {array} $$ (29)
Em δ =0, o coeficiente r torna-se o coeficiente de reflexão de Fresnel da onda p-polarizada (ver, por exemplo, Eq. (2.49) de [4]). Sob a mesma condição, t não é o coeficiente de transmissão de Fresnel, uma vez que nossas definições de t e r diferem dos de Fresnel.

Extinção da Luz pela Nanosfera de Metal

Em um artigo anterior, um dos autores generalizou a teoria de Lorentz-Mie permitindo o ABC da Eq. (23). Um análogo do coeficiente de Fresnel r , o coeficiente de Mie b _l para o modo TM refletido do l a ordem foi encontrada para ser
$$ b_ {l} =- \ frac {(1+ \ delta_ {l}) \, \ epsilon_ {1} \, \ frac {k_ {2} \, \ psi_ {l} ^ {\ prime} (k_ {2} R)} {\ psi_ {l} (k_ {2} R)} - \ epsilon_ {2} \, \ frac {k_ {1} \, \ psi_ {l} ^ {\ prime} (k_ { 1} R)} {\ psi_ {l} (k_ {1} R)}} {(1+ \ delta_ {l}) \, \ epsilon_ {1} \, \ frac {k_ {2} \, \ psi_ {l} ^ {\ prime} (k_ {2} R)} {\ psi_ {l} (k_ {2} R)} - \ epsilon_ {2} \, \ frac {k_ {1} \, \ zeta_ { l} ^ {\ prime} (k_ {1} R)} {\ zeta_ {l} (k_ {1} R)}}, $$ (30)
Onde
$$ \ delta_ {l} =\ frac {\ epsilon ^ {\ mathrm {T}} - \ epsilon _ {\ mathrm {g}}} {\ epsilon _ {\ mathrm {g}}} \, \ frac {l \ , (l + 1) \, j_ {l} (k_ {2} R) \, j_ {l} (k_ {2} ^ {\ mathrm {L}} R)} {\ psi_ {l} ^ {\ prime} (k_ {2} R) \, k_ {2} ^ {\ mathrm {L}} R \, j_ {l} ^ {\ prime} \ left (k_ {2} ^ {\ mathrm {L}} R \ direita)}, $$ (31)
ψ _l e ζ _l são as funções Riccati-Bessel e Riccati-Hankel da ordem l , respectivamente; j _l é a função esférica de Bessel, o primo denota a derivada de uma função com respeito ao seu argumento.

Vamos comparar as previsões das teorias de Lorentz-Mie clássica e generalizada com dados experimentais. Em [15], Hilger, Tenfelde e Kreibig estudaram espectros de extinção de nanopartículas de prata depositadas em superfícies dielétricas. Na primeira etapa do estudo, os pesquisadores geraram feixes de partículas de prata com diâmetros médios de 2, 3,5 e 4 nm, determinaram a distribuição do tamanho de partícula para um dos feixes, registraram espectros de extinção e estimaram o parâmetro A =0,25 da fórmula fenomenológica Γ = Γ _b + A v _F / R , onde Γ _b é a taxa de relaxamento de metal em massa, para esferas de prata no vácuo. Primeiro, calculamos os espectros de extinção para um feixe de esferas de prata com o diâmetro médio 〈 D 〉 =2 nm e distribuição de tamanho experimental que abrange a região de D =1 a D =4 nm. Nossa teoria não contém parâmetros ajustáveis. Para definir as funções dielétricas, usamos a tabulação do índice de refração da prata bruta proposta por Lynch e Hunter [16] (ver Fig. 1). Também aplicamos as Eqs. (16), (21) e (22) com ω _p =9,17 eV, Γ _b =0,021 eV, v _F =1,39 × 10 ⁶ m / s e A =0,25. Os resultados dos cálculos e do espectro experimental são apresentados na Fig. 2.

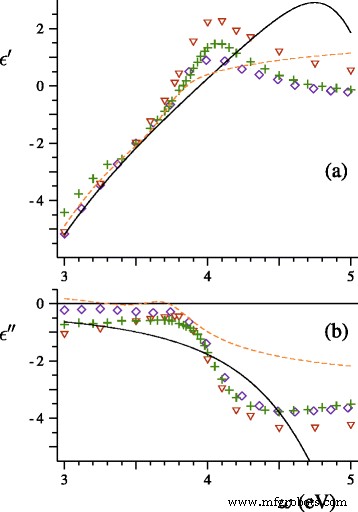
Real ( a ) e imaginário ( b ) partes da função dielétrica da prata de acordo com Johnson e Christy (◇) [20], Lynch e Hunter (+) [16], Weber (△) [21], Hao e Nordlander ( linha tracejada ) [22] e Drachev et al. ( linha sólida ) [23]

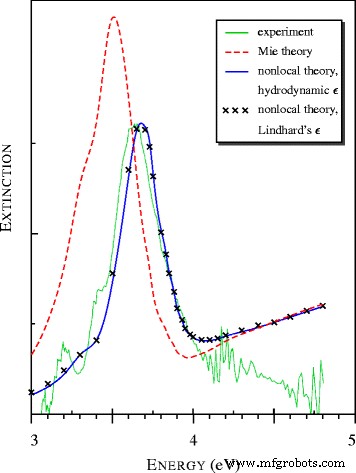
Espectros de extinção de luz por partículas nanométricas de prata observados em [15] e calculados com modelos locais e não locais. Todos os espectros teóricos são apresentados em unidades relativas comuns

Os espectros teóricos na Fig. 2 foram calculados usando o Klimontovich-Silin-Lindhard e funções dielétricas hidrodinâmicas muito mais simples. É surpreendente que ambos os cálculos forneçam resultados próximos, embora | a |> 1 na região de ressonância do plasmon.

Para as esferas de prata de tamanho nanométrico, sabe-se que o máximo no espectro de extinção, denominado ressonância de Fröhlich [17], plasmon e superfície plasmônica polariton (SPP) [15], muda de 3,5 para 3,65 eV [18]. O modelo não local está em excelente acordo com os dados experimentais, enquanto a teoria local (Mie) fornece o máximo em ω ± 3,5 eV (ver Fig. 2 e Tabela 1).

O cálculo do desvio para o azul da ressonância do plasmon pode ser apoiado pela seguinte consideração. Na aproximação eletrostática, apenas b ₁ contribui para a seção transversal de extinção Q _ext e Eq. (30) pode ser simplificado usando as seguintes aproximações
$$ \ frac {k_ {2} R \, \ psi_ {l} ^ {\ prime} (k_ {2} R)} {\ psi_ {l} (k_ {2} R)} \ simeq l + 1; \, \, \, \ frac {k_ {1} R \, \ zeta_ {l} ^ {\ prime} (k_ {1} R)} {\ zeta_ {l} (k_ {1} R)} \ simeq -\,eu. $$ (32)
Portanto, Q _ext tem um máximo em
$$ \ Re [2 \, (1+ \ delta_ {1}) \, \ epsilon_ {1} + \ epsilon_ {2}] =0. $$ (33)
A condição obtida (33) leva em consideração a excitação do L modos (pelo termo δ ₁ ) e, portanto, difere da condição de ressonância de Fröhlich [17] :.
$$ \ Re (2 \, \ epsilon_ {1} + \ epsilon_ {2}) =0. $$ (34)
No experimento [15], as frequências de pico ω _m e larguras de ressonância Δ ω dos espectros de extinção eram quase independentes de 〈 D 〉. Este recurso de Δ ω parece discordar da teoria clássica de Mie. Realmente, a teoria local prevê o alargamento das ressonâncias do plasmon com a diminuição de D (em A =0,25) como mostrado na Tabela 1. Ao mesmo tempo, a teoria não local fornece larguras de ressonância aproximadamente iguais, mas posições de pico diferentes. A superposição das contribuições de todas as partículas dá o valor de Δ ω que estão em notável concordância com os dados experimentais. É interessante que a teoria não local prediz um alargamento da ressonância de plasmon de um feixe mesmo em A =0.

Em ω > 4 eV, as curvas teóricas suaves na Fig. 2 ficam mais altas do que a mistura de picos experimentais estreitos e próximos. A absorção interband domina nesta faixa espectral como pode ser confirmado pela Fig. 1. As peculiaridades observadas do espectro são provavelmente uma consequência de uma transição das bandas contínuas para uma estrutura de nível discreto. Esse efeito do tamanho quântico foi descoberto anteriormente em um estudo das propriedades ópticas das nanoesferas de ouro [19]. Quando o tamanho da esfera de prata foi aumentado para 〈 D 〉 =3,5 nm, a absorção primeiro aumentou em relação ao máximo e formou um platô com uma série de pequenos mergulhos equidistantes. Então, a absorção diminuiu ligeiramente em 〈 D 〉 =4 nm.

A fim de estudar a formação da asa azul da ressonância do plasmon, calculamos os espectros de extinção das partículas de prata ultra-estanho e os apresentamos na Fig. 3. Uma característica notável na Fig. 3 é o desaparecimento completo da ressonância do plasmon em D =1 nm. Anteriormente, esse efeito foi observado no estudo experimental de nanoesferas de ouro [19]. Em particular, na Fig. 9 de [19], os espectros experimentais de partículas com diâmetros de 1,7, 1,9, 2,0, 2,1, 2,3 e 2,5 nanômetros foram comparados com os espectros calculados com a teoria de Mie local. A concordância foi pobre, não descrevendo o alargamento da ressonância do plasmon e sua posição [19]. As tentativas de melhorar o ajuste variando o tamanho das partículas e as modificações das funções dielétricas não foram sucessivas. De acordo com os autores de [19], a banda de oscilação coletiva anormalmente larga ou deprimida observada resiste a ser ajustada com as correções propostas da teoria de Mie local. Como pode ser visto na Fig. 4, a situação muda dramaticamente se a teoria de Mie não local for aplicada. Observe que não usamos parâmetros ajustáveis. A tabulação do índice de refração complexo por Johnson e Christy [20] foi usada para determinar a função dielétrica do ouro. Outros parâmetros, incluindo A =1 e o índice de refração de tolueno (1,37) foram retirados de [19].

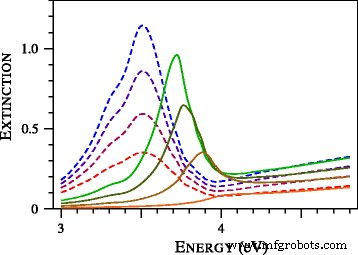
Seção transversal de extinção normalizada de partículas de prata com diâmetros de 2,2, 1,8, 1,4 e 1,0 nm calculado com local ( linhas tracejadas ) e não local ( curvas sólidas ) Teorias de Mie. Quanto menor for a partícula, menor será a curva. Todas as seções transversais teóricas são apresentadas em unidades relativas comuns

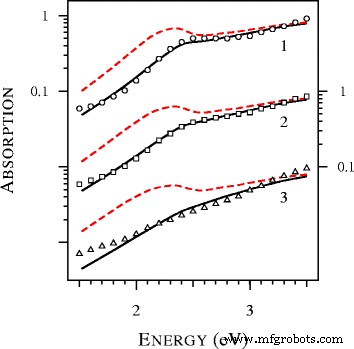
Espectros de absorção calculados com o local ( linhas tracejadas ) e não local ( linhas sólidas ) Teoria de Mie e dados experimentais ( pontos ) extraído da Fig. 9 de [19] para esferas de ouro com D =2,5, 2,1 e 1,7 nm em tolueno (curvas 1 e círculos , curvas 2 e quadrados , e as curvas 3 e triângulos , respectivamente). Todos os espectros teóricos são normalizados para a unidade em 4,12 eV e deslocados verticalmente

Números das ondas longitudinais

Os modos longitudinais diferem dos transversais por valores muito mais altos dos números de onda. Por exemplo, para os cálculos apresentados na Fig. 2, a parte real de \ (k_ {2} ^ {\ mathrm {L}} \) corresponde ao período espacial \ (\ Lambda =2 \ pi / \ Re k_ { 2} ^ {\ mathrm {L}} \) diminuindo de 9 para 2 nm em ω aumentando de 3 para 4 eV. Neste ω intervalo, o valor absoluto da razão \ (k_ {2} ^ {\ mathrm {L}} / k_ {2} \) diminuiu de 130 para 100 e o parâmetro δ da Eq. (27) diminuiu de 0,01 para 0,005 em θ ₁ = π / 4. Concluímos, portanto, que a excitação das ondas L em uma superfície plana de prata pode ser desprezada. No entanto, o L modos foram considerados importantes em aglomerados de prata de tamanho nanométrico.

Uma substituição do termo \ (- \, \ omega ^ {2} _ {\ mathrm {p}} / (\ omega ^ {2} + i \ Gamma \ omega) \) na Eq. (16) por ε ^T - ε _g de acordo com a Eq. (21) nos permite reescrever a dispersão da Eq. (15) na seguinte forma
$$ 1+ \ frac {3} {5} \, a ^ {2} + \ frac {3} {7} \, a ^ {4} + \ frac {3} {9} \, a ^ {6 } + \ dots =\ frac {1} {1- \ epsilon ^ {\ mathrm {T}} / \ epsilon _ {\ mathrm {g}}}. $$ (35)
No caso mais simples de ε _g =1 e Γ =0, Eq. (35) prevê que o metal é transparente para as ondas transversais e L em ω > ω _p mas ambos k ^L e k ^T são complexos em ω < ω _p .

Se o sólido for transparente, uma onda longitudinal pode ser excitada sob a incidência oblíqua de uma onda p-polarizada em uma superfície plana. Existem várias características distintas desse efeito. Em primeiro lugar, as ondas longitudinais podem ser geradas em uma superfície plana, enquanto esforços especiais devem ser feitos para excitar os polaritons de plasmon de superfície [4, 5]. Em segundo lugar, no padrão de interferência, a intensidade do campo eletromagnético é modulada não ao longo, mas perpendicular à interface. Portanto, vazios podem aparecer em planos paralelos à superfície devido à fragmentação do sólido. De acordo com a definição de ω _p , condição ω > ω _p pode ser encontrado em sólidos (por exemplo, semicondutores) com uma baixa densidade dos portadores de corrente. Não examinamos este caso aqui porque a fórmula de ε ^L foi derivado para gás de elétron degenerado.

Conclusões

A fim de definir uma função dielétrica espacialmente dependente, todos os pesquisadores anteriores consideraram a interação da matéria com uma onda eletromagnética plana. Esta abordagem não é construtiva e rigorosa em nano-óptica quando o campo está localizado em uma cavidade e as condições de contorno devem ser levadas em consideração de alguma forma. Resolvemos esse problema calculando a resposta do meio em um campo elétrico que satisfaz a equação vetorial de Helmholtz. A função dielétrica espacialmente dispersiva derivada depende do quadrado do número de onda, um parâmetro da equação de Helmholtz, mas não do vetor de onda de uma onda plana.

Relatamos os coeficientes de reflexão de Fresnel modificados devido à excitação das ondas longitudinais nos metais. Generalização semelhante foi feita anteriormente para os coeficientes de Mie. Aqui, a teoria foi verificada com simulação de extinção de luz por aglomerados de prata e ouro do tamanho de nanômetros. O deslocamento calculado de 3,5 para 3,65 eV e a largura da ressonância do plasmon de superfície do feixe de partículas de prata estão em excelente acordo com os dados experimentais. Além disso, o modelo não local explica o desaparecimento da ressonância plasmônica de esferas douradas com diâmetros de cerca de 2 nm. É importante que a onda L possa ser excitada em uma superfície plana por uma onda incidente plana. Esta é a principal diferença entre os polaritons do plasmão e os polaritons do plasmão de superfície.

As propriedades das oscilações eletromagnéticas em metais foram examinadas. It has been found that the absolute values of the wavenumbers of the longitudinal waves are much larger than those of the transverse waves. For example, in silver at a photon energy of 3.5 eV, the ratio of the absolute values of the wavenumbers is equal to 130. There, the real part of the wavenumber of the longitudinal wave corresponds to a wavelength of 7 nm. The large difference in the wavenumbers prevents excitation of the L waves at a planar surface. However, the L modes have been shown to be excited in silver and gold nanometer-sized particles.

Biossensor ultrassensível para a detecção de DNA de Vibrio cholerae com nanoesferas de composto de ácido poliestireno-co-acrílico Investigação teórica de nanofios de germânio deformados biaxialmente por tração