Metassuperfície multifuncional de grafeno para gerar e orientar ondas de vórtice

Resumo

O grafeno, um material 2D inovador com espessura atômica, é um candidato muito promissor e tem atraído grande atenção em várias aplicações. A metassuperfície de grafeno permite o controle dinâmico de várias frentes de onda, alcançando funcionalidades diferenciadas. A flexibilidade da metassuperfície de grafeno torna possível implementar dispositivos multifuncionais com facilidade. Neste trabalho, um novo projeto de metassuperfície multifuncional de grafeno, que pode combinar as funcionalidades de geração e direção de ondas de vórtice, foi proposto. A metassuperfície multifuncional de grafeno consiste em uma grande variedade de células unitárias reflexivas de grafeno. Cada célula unitária é controlada independentemente por seu tamanho e tensão de porta estática externa. Ao examinar a propriedade reflexiva da célula de grafeno, a metassuperfície de grafeno é projetada para realizar multifuncionalidades. Os resultados da simulação mostram que a onda de vórtice pode ser gerada e dirigida. Este trabalho pode estabelecer uma metodologia para projetar metassuperfícies multifuncionais de grafeno, e a capacidade de ajuste do grafeno abre as portas para o projeto e fabricação de dispositivos de grafeno reconfiguráveis.

Introdução

O grafeno, um material inovador e inovador em 2D com espessura atômica, está atraindo cada vez mais atenção na biologia, optoeletrônica, comunicação terahertz, etc [1]. Em regime de terahertz, o grafeno tem melhor desempenho do que o metal nobre convencional devido ao suporte de propagação de polaritons de plasmon de superfície (SPPs) [2], o que o torna um candidato muito promissor na tecnologia de terahertz. Portanto, nos últimos anos, surgiu um grande número de dispositivos baseados em grafeno em regimes terahertz e infravermelho médio, como moduladores [3-6], detectores [7], absorvedores [8, 9] e lasers [10, 11].

É de grande importância projetar e fabricar metamateriais reconfiguráveis para controlar o comportamento das ondas eletromagnéticas [12, 13]. Portanto, muitos mecanismos de ajuste foram realizados em várias faixas de frequência diferentes [14], como metamateriais eletricamente reconfiguráveis [15], metamateriais mecanicamente reconfiguráveis [16], materiais não lineares [17], cristais líquidos [18], microfluidos [ 19], estruturas semicondutoras [20] e grafeno [21]. O grafeno, como um material inovador, é um candidato diferenciado entre eles, principalmente devido à sua condutividade elétrica / magnética controlada, que permite o projeto e a fabricação de dispositivos controláveis miniaturizados [14, 22]. Portanto, ele tem grande potencial para projetar metassuperfície reconfigurável, e muitas aplicações baseadas em sua sintonia foram propostas em [23] e [24]. Aplicando a lei de Snell generalizada [25, 26], a reflexão anômala pode ser ajustada e realizada por metassuperfícies de grafeno [27]. Esses trabalhos podem abrir caminho para o design e a fabricação de dispositivos terahertz sintonizáveis.

Em telecomunicações, o momento angular orbital (OAM) é importante para aumentar a capacidade do canal, uma vez que pode fornecer estado infinito [28, 29]. O metamaterial tridimensional pode ser usado para gerar a onda OAM [30]. A metassuperfície, que pode ser considerada um metamaterial bidimensional, pode apresentar excelente desempenho em espessuras de subcomprimentos de onda. No regime de microondas, a metassuperfície tem sido amplamente usada para projetar e fabricar dispositivos de tamanhos de sub-onda para gerar ondas com várias propriedades de polarização e ganho [31-34]. Em regime de terahertz, uma metassuperfície de grafeno reflexiva foi relatada para gerar ondas de vórtice com sintonia [35]. A metassuperfície de grafeno tem flexibilidade para controlar a frente de onda [36]; portanto, um projeto viável, que combina as funcionalidades de geração de onda de vórtice e reflexão anômala, pode ser esperado para ajustar a diretividade de ondas de vórtice com altas precisões.

Neste trabalho, com base em nossa pesquisa anterior sobre metassuperfície em micro-nano óptica [37-41], estudamos o mecanismo para combinar as funcionalidades de duas metassuperfícies. Uma célula de grafeno é analisada para obter a relação entre o coeficiente de reflexão e seu potencial químico junto com seu tamanho de patch. Um 360 ^∘ completo a faixa de fase de reflexão é calibrada como referência para projetar uma metassuperfície de grafeno para combinar as funcionalidades de geração de onda de vórtice e reflexão anômala. A metassuperfície combinada é realizada por uma grande variedade de células reflexivas de grafeno. Os resultados simulados mostram que as ondas de vórtice podem ser geradas e dirigidas por um determinado ângulo de reflexão.

Métodos

A condutividade do grafeno consiste na transição interbanda e intrabanda. A transição intrabanda domina o regime terahertz e infravermelho, enquanto a transição interbanda domina o regime óptico visível. Na região de terahertz e infravermelho, a condutividade pode ser modelada pelo modelo de Drude [24],
$$ \ sigma (\ omega) =\ frac {2e ^ {2}} {\ pi \ hbar ^ {2}} k_ {B} T \ cdot \ ln \ left [2 \ cosh \ left (\ frac {E_ {f}} {2k_ {B} T} \ right) \ right] \ frac {i} {\ omega + i \ tau ^ {- 1}}, $$
onde k _B é constante de Boltzmann, T é a temperatura, τ é o tempo de relaxamento, e E _f é a energia de Fermi.

Neste trabalho, o dispositivo opera em regime de terahertz, onde E _f ≫ k _B T ; portanto, a equação pode ser simplificada como
$$ \ sigma (\ omega) =\ frac {e ^ {2} E_ {f}} {\ pi \ hbar ^ {2}} \ frac {i} {\ omega + i \ tau ^ {- 1}} , $$
assumindo o valor típico da temperatura ambiente T =300 K , e o tempo de relaxamento do grafeno τ =1 ps. Neste trabalho, a energia Fermi E _f é controlado pela tensão da porta estática externa. Na simulação, o grafeno não é modelado como blocos de metamateriais 3D, mas como condições condutoras de superfície 2D devido à espessura atômica.

A metassuperfície de grafeno é composta por uma grande variedade de células de grafeno, o que resulta em comportamento plasmônico coletivo excitado na superfície, realizando propriedades eletromagnéticas extraordinárias. A frequência é 1,3 THz; assim, devido à propagação de onda lenta associada ao modo plasmônico, a ressonância pode ocorrer em tamanhos muito pequenos, i. e., abaixo de λ / 10 [23, 42]. A fim de projetar a metassuperfície das células de grafeno, um gráfico de calibração do comportamento reflexivo de uma célula de grafeno é extraído para estudar a influência detalhada de cada parâmetro em uma única célula de grafeno.

Uma célula de grafeno unitária típica, como mostrado na Fig. 1, é composta de estrutura de múltiplas camadas com remendo de grafeno de espessura atômica montado no topo. O patch de grafeno com tamanho de w _x × w _y é montado no centro em cima de uma pilha de substratos quadrados em camadas com comprimentos laterais p de 14 µm. Um substrato de quartzo ( ε _r =3,75, tan δ =0,0184) de 25 µm de espessura é colocado na parte superior da camada de terra metálica na parte inferior. Uma tensão DC de polarização externa é aplicada entre o patch de grafeno e uma camada de silício policristalino de espessura de 50 nm. Um Al ₂ de 10 nm de espessura O ₃ (Alumina, \ (\ epsilon _ {r} =8,9, \ tan \ delta =0,01 \)) a camada é inserida no meio como espaçador. O potencial químico pode ser ajustado de 0,01 a 1,0 eV, controlando a tensão CC de polarização externa de 0 a 14,7 V [23, 35]. Deve ser mencionado que a camada de silício policristalino e o espaçador de Alumina não são modelados na simulação deste trabalho e os motivos são os seguintes. Em primeiro lugar, uma simulação 2D separada, que é muito menos cara, é realizada para mostrar que, uma vez que a espessura da camada de silício policristalino e do espaçador de Alumina é muito menor do que o substrato de quartzo, sua influência no comportamento reflexivo pode ser desprezada. Por outro lado, nas simulações de elementos finitos, uma quantidade extrema de elementos é necessária ao lidar com objetos adjacentes com grandes diferenças de tamanho. Como resultado, as simulações 3D que modelam essas duas camadas serão extremamente caras.

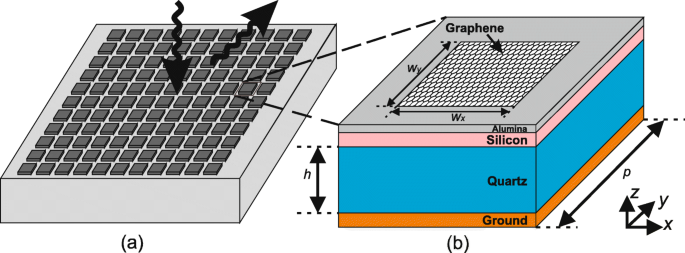
Ilustração da metassuperfície de grafeno e configuração da célula. a Esquemático de uma metassuperfície de grafeno, que pode direcionar as ondas eletromagnéticas de entrada por reflexão anômala. b Configuração de uma célula de grafeno, que consiste em um substrato com várias camadas e um patch de grafeno montado de tamanho w _x × w _y . Uma tensão de porta estática é aplicada entre o patch de grafeno e a camada de silício para controlar o potencial químico

Para estudar as propriedades reflexivas influenciadas por μ _c e w _x , as condições periódicas são atribuídas em x e y instruções. A onda colide normalmente a partir do topo com polarização paralela, ou seja, campo elétrico polarizado em x -direção. Uma vez que o grafeno é equivalente a uma condição de condutância de superfície complexa, apenas w _x pode afetar a condutância em x -direcção significativamente, enquanto w _y tem influência desprezível e é fixada em 4 µm em todas as simulações neste artigo.

Para examinar as influências do tamanho do remendo e do potencial químico, varremos w _x de 0,2 a 13,8 µm por etapa de 0,2 µm e varredura μ _c de 0,01 a 1,00 eV por etapa de 0,01 eV, e a frequência é fixada em 1,3 THz. A fase e magnitude de S ₁₁ são plotados na Fig. 2, que são chamados de gráficos de calibração, uma vez que o valor de w _x e μ _c pode ser calibrado a partir deles. Para garantir a eficiência da metassuperfície, a magnitude do coeficiente de reflexão deve ser maior que 0,7; assim, as regiões não qualificadas são escavadas em branco. No gráfico de calibração, obtém-se uma cobertura total de 360 ^∘ que é suficiente para construir metassuperfícies de grafeno.

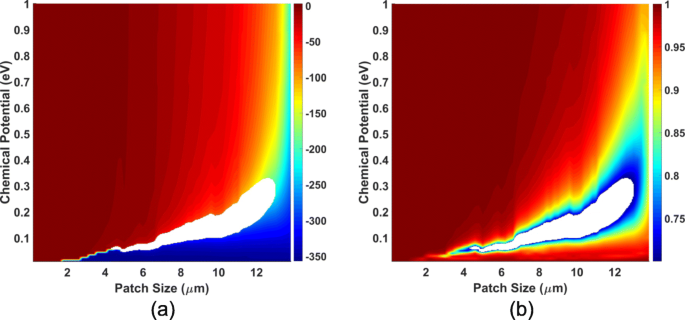
Diagrama de calibração dos coeficientes de reflexão da célula de grafeno. O coeficiente de reflexão da célula de grafeno influenciado pelo tamanho do patch de grafeno w _x e o potencial químico μ _c , onde a região onde a magnitude da reflexão é menor que 0,7 é subtraída. a fase e b diagrama de magnitude

O diagrama de fase deve ser suave o suficiente para controlar a fase com precisão. A fim de projetar os parâmetros das células de grafeno para alcançar a cobertura total da fase de 0 ^∘ para 360 ^∘ , sete combinações de w _x e μ _c são selecionados, como mostrado na Fig. 3.

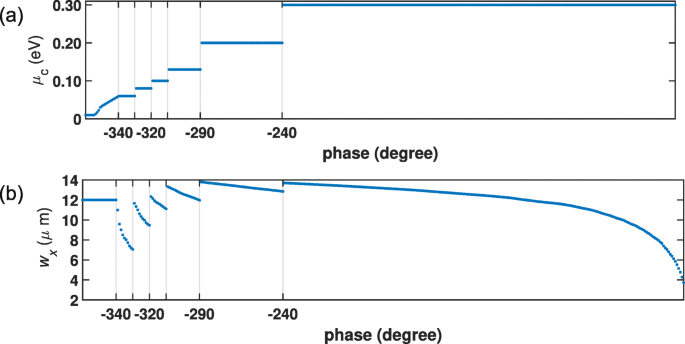
Diagrama do projeto da célula de grafeno. Um 360 ^∘ completo cobertura de fase alcançada por sete grupos de combinações de a potencial químico e b tamanho do remendo

Resultados e discussões

Para realizar várias funções, seria muito útil combinar as funcionalidades de duas metassuperfícies, ou adicionar novas funções em outra. Esta metodologia irá fornecer uma maneira versátil para projetar novas metassuperfícies. Combinamos as funcionalidades de geração de onda de vórtice e deflexão de onda por reflexão anômala neste artigo.

Uma metodologia generalizada é proposta a seguir para combinar duas metassuperfícies MS ₁ e MS ₂ em uma metassuperfície multifuncional MS _t . Para perceber a combinação, começamos com a lei generalizada da reflexão [25]. Conforme ilustrado na Fig. 4, considere uma onda plana com comprimento de onda de espaço livre λ colide com o ângulo de incidência θ _i , a seguinte equação descreve a lei generalizada de reflexão,
$$ \ sin \ theta_ {r} - \ sin \ theta_ {i} =\ frac {\ lambda} {2 \ pi n_ {i}} \ frac {\, \ mathrm {d} \ phi} {\ text { dx}}, $$ (1)

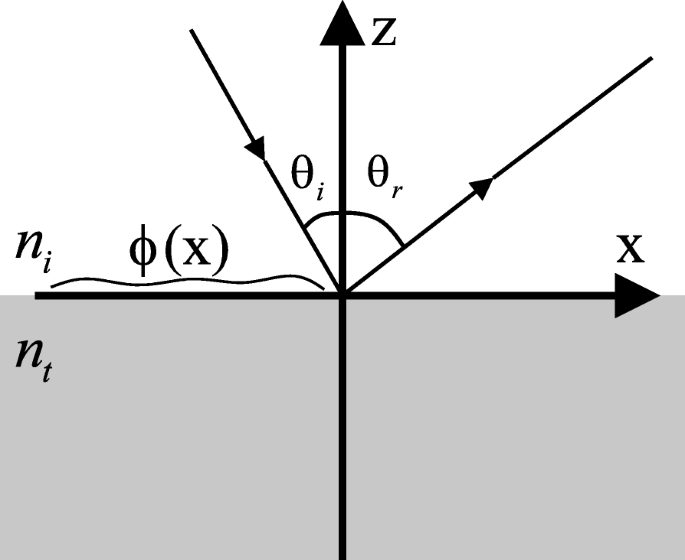
Ilustração da lei generalizada de reflexão. Uma onda eletromagnética incide do topo com o anjo incidente θ _i , enquanto é refletido por θ _r diferente de θ _i , devido à descontinuidade de fase ϕ ( x ) ao longo da interface

onde θ _r é o ângulo de reflexão, n _i é o índice de refração no espaço superior, e ϕ ( x ) descreve a descontinuidade de fase ao longo da interface.

Considere o caso simplificado em que a onda colide normalmente, e o espaço superior é o espaço livre ( n _i =1), como mostrado na Fig. 5, para as duas primeiras metassuperfícies MS ₁ e MS ₂ , Eq. 1 pode ser ainda mais simplificado como
$$ \ frac {\, \ mathrm {d} \ phi_ {m}} {\ text {dx}} =\ frac {2 \ pi} {\ lambda} \ sin \ theta_ {rm} (x) \ quad \ quad m =1,2. $$ (2)

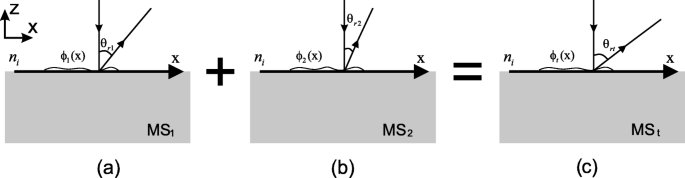
Ilustração da combinação de duas metassuperfícies em uma metassuperfície multifuncional. Na inserção, as ondas eletromagnéticas estão colidindo normalmente do espaço superior com índice de refração n _i . a Metasruface 1 (MS ₁ ) com descontinuidade de fase ϕ ₁ ( x ) e b metasuperfície 2 (MS ₂ ) com descontinuidade de fase ϕ ₂ ( x ) são combinados em c a meta-superfície multifuncional desejada (MS _t ) com descontinuidade de fase ϕ _t ( x ) θ _{r 1} ( x ), θ _{r 2} ( x ) e θ _rt ( x ) são os ângulos de reflexão anômala ao longo das interfaces das metassuperfícies, respectivamente, e a relação θ _rt ( x ) = θ _{r 1} ( x ) + θ _{r 2} ( x ) mantém-se em qualquer lugar em MS _t

Para obter ϕ _t de MS _t , escolhemos um segmento D _x ao longo da interface, e o problema se torna o seguinte:assuma em x ∈ D _x , mantém - π / 2 < θ _{r 1} ( x ) + θ _{r 2} ( x ) < π / 2, encontre ϕ _t , s. t. para ∀ x ∈ D _x , naquela
$$ \ begin {alinhados} \ frac {\, \ mathrm {d} \ phi_ {t}} {\ text {dx}} &=\ frac {2 \ pi} {\ lambda} \ sin \ theta_ {rt} , \ quad \ text {e} \\ \ theta_ {rt} (x) &=\ theta_ {r1} (x) + \ theta_ {r2} (x). \ end {alinhado} $$ (3)
Ele pode ser derivado das Eqs. 2 e 3 que
$$ \ begin {alinhados} \ frac {\, \ mathrm {d} \ phi_ {t}} {\ text {dx}} &=\ frac {2 \ pi} {\ lambda} \ sin \ theta_ {rt} =\ frac {2 \ pi} {\ lambda} \ sin (\ theta_ {r1} + \ theta_ {r2}) \\ &=\ frac {2 \ pi} {\ lambda} \ left (\ cos \ theta_ { r2} \ sin \ theta_ {r1} + \ cos \ theta_ {r1} \ sin \ theta_ {r2} \ right) \\ &=\ cos \ theta_ {r2} \ frac {\, \ mathrm {d} \ phi_ {1}} {\ text {dx}} + \ cos \ theta_ {r1} \ frac {\, \ mathrm {d} \ phi_ {2}} {\ text {dx}} \\ &=\ frac {\ , \ mathrm {d}} {\ text {dx}} \ left (\ cos \ theta_ {r2} \ phi_ {1} + \ cos \ theta_ {r1} \ phi_ {2} \ right) \\ &\ quad - \ left (\ sin \ theta_ {r2} \ frac {\, \ mathrm {d} \ theta_ {r2}} {\ text {dx}} \ phi_ {1} + \ sin \ theta_ {r1} \ frac { \, \ mathrm {d} \ theta_ {r1}} {\ text {dx}} \ phi_ {2} \ right), \ end {alinhado} $$ (4)
o que leva a
$$ \ begin {alinhado} \ phi_ {t} (x) =&\ cos \ theta_ {r2} \ phi_ {1} (x) + \ cos \ theta_ {r1} \ phi_ {2} (x) \\ &- \ int_ {D_ {x}} \ left (\ sin \ theta_ {r2} \ frac {\, \ mathrm {d} \ theta_ {r2}} {\ text {dx}} \ phi_ {1} + \ sen \ theta_ {r1} \ frac {\, \ mathrm {d} \ theta_ {r1}} {\ text {dx}} \ phi_ {2} \ right) \ text {dx}, \ end {alinhado} $$ (5)
onde o termo de integração calcula a contribuição da variância de θ _ri ( x ) e geralmente podem ser calculados numericamente. A Equação 5 desempenha um papel vital para combinar as funcionalidades de duas metassuperfícies.

Além disso, se o ângulo de direção for constante, o termo de integração na Eq. 6 desaparece. A Equação 5 pode ser significativamente simplificada como
$$ \ phi_ {t} (x) =\ cos \ theta_ {r2} \ phi_ {1} (x) + \ cos \ theta_ {r1} \ phi_ {2} (x) + C. $$ (6)
Esta é a equação governante para combinar metassuperfícies, e a distribuição de fase pode ser calculada para combinar geração de onda de vórtice e reflexão anômala.

Neste artigo, MS ₁ é a metassuperfície que gera ondas de vórtice, enquanto MS ₂ é a metassuperfície que orienta as ondas.

Conforme ilustrado em [35], ondas de vórtice com modo l pode ser gerado por uma placa de N setores com sucessivos incrementos de mudança de fase. A mudança de fase do n º setor ϕ _n pode ser calculado como ϕ _n = ϕ ₀ +2 π n l / N , onde ϕ ₀ é a mudança de fase do setor inicial. Além disso, a fim de gerar uma onda de vórtice, deve-se considerar que - N / 2 < l < N / 2. Portanto, N =4 é suficiente para gerar modos l =0, ± 1.

Para gerar uma onda de vórtice com l =1, a placa é subdividida em quatro setores, conforme mostrado na Fig. 6a. A condição de fase ϕ ₁ ( x , y ) é uma função constante fragmentada que diminui em 90 ^∘ através dos setores, no sentido anti-horário.
$$ \ phi_ {1} (x, y) =\ left \ {\ begin {alinhados} &0 ^ {\ circ} &\ quad &x \ geq 0, y \ geq 0 \\ &-90 ^ {\ circ } &\ quad &x <0, y \ geq 0 \\ &-180 ^ {\ circ} &\ quad &x <0, y <0 \\ &-270 ^ {\ circ} &\ quad &x \ geq0, y <0 \ end {alinhado} \ right. $$ (7)

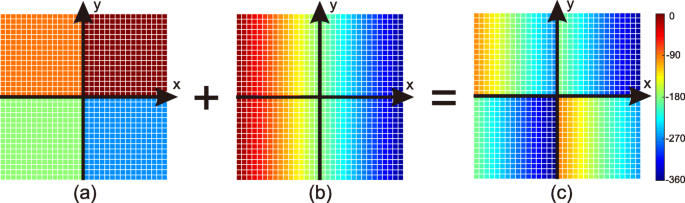
Ilustração da combinação das funções de descontinuidade de fase. a ϕ ₁ , distribuição de descontinuidade de fase de MS ₁ , que gera onda eletromagnética de vórtice com l =1. b ϕ ₂ , distribuição de descontinuidade de fase de MS ₂ , o que resulta em reflexão anômala. c Distribuição de descontinuidade de fase combinada do MS _t calculado pela Eq. 6

Quando x -a onda polarizada está colidindo normalmente de cima, onda de vórtice com l =1 será refletido. Deve-se notar que a onda é refletida verticalmente; portanto, o ângulo de deflexão é 0 ^∘ , ou seja, θ _{r 1} ( x ) =0 ^∘ .

Para gerar reflexão anômala com ângulo de deflexão θ _r , Eq. 1 é aplicado. Conforme ilustrado na Fig. 4, quando a onda está colidindo normalmente no espaço livre, ou seja, θ _i =0 ^∘ e n _i =1, Eq. 1 é reduzido a
$$ \ phi_ {2} (x) =\ frac {2 \ pi \ sin \ theta_ {r}} {\ lambda} x + C. $$
Neste trabalho, o ângulo de deflexão é definido como θ _r =30 ^∘ . A partir da equação acima, sabendo que o período da célula unitária é de 14 µm, a diferença de mudança de fase entre manchas adjacentes é calculada como 10,9 ^∘ . A distribuição de fase é mostrada na Fig. 6b.

Para combinar MS ₁ e MS ₂ , pegamos θ _{r 1} ( x ) =0 ^∘ e θ _{r 2} ( x ) =30 ^∘ na Eq. 6 e obtenha a fórmula de design de MS _t ,
$$ \ phi_ {t} (x) =\ frac {\ sqrt {3}} {2} \ phi_ {1} (x) + \ phi_ {2} (x) + C. $$
A partir dessa fórmula, pode-se calcular a distribuição de fases, que é mostrada na Fig. 6c. De acordo com a Fig. 3, escolhendo os potenciais químicos μ _c e o tamanho do patch w _x de cada célula, uma metassuperfície de grafeno 32 × 32 é configurada. A Figura 1a mostra a vista superior da colocação das células de grafeno na metassuperfície. Pode-se ver que cada setor é um subdomínio 16 × 16, composto por 16 colunas verticalmente. E cada coluna consiste em 16 manchas de grafeno idênticas, onde uma certa combinação de w _x e μ _c é atribuído.

O prato é animado por um x onda polarizada incidindo de cima. O campo elétrico da onda incidente é normalizado, ou seja, \ (\ vec {\ mathrm {E}} _ {\ text {inc}} =\ vec {x} \). A simulação foi realizada usando o solver comercial de elementos finitos COMSOL Multiphysics 5.2. O grafeno tem espessura atômica; entretanto, a espessura dos substratos é da escala de micrômetros. Portanto, o esforço computacional seria enorme se a malha tridimensional fosse aplicada a manchas de grafeno. Portanto, a espessura das manchas de grafeno é ignorada e uma condição de condutividade de superfície bidimensional equivalente é aplicada como condições de contorno de transição no COMSOL Multiphysics. Existem 32 × 32 patches na placa, que é subdividida em quatro setores. Em cada setor, existem 16 × 16 remendos controlados independentemente por seus tamanhos e potenciais químicos. A simulação consumiu 7,1 milhões de graus de liberdade, realizada em um servidor de threads de 40 × 2,1 GHz e 256 GB de memória.

A Figura 7b mostra a magnitude do campo elétrico da onda refletida normalizada pela onda incidente. A metassuperfície de grafeno gera uma onda de vórtice com l =1 e desvia em 30 ^∘ em direção a x -eixo.

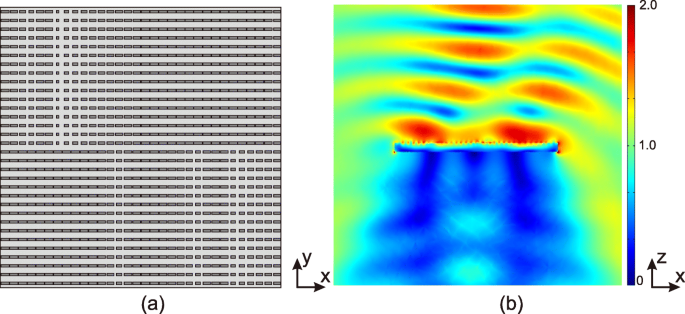
Resultados da metassuperfície multifuncional. a Configuração da placa com reflectarray de grafeno consistindo de 36 × 36 patches de grafeno. As larguras ( w _y ) de todo o patch de grafeno são tomados como 4 µm, e os valores de w _x são selecionados para realizar a condição de descontinuidade de fase, conforme mostrado na Fig. 6. b A magnitude do campo elétrico da onda de vórtice refletida de l =1. A onda incidente é um x - onda eletromagnética polarizada com campo elétrico normalizado, colidindo normalmente a partir do topo. A onda é desviada por 30 ^∘ em direção a x -direção

Conclusões

Em resumo, estudamos o princípio de design de metassuperfícies multifuncionais de grafeno. A metodologia de combinação de duas metassuperfícies é proposta. Como exemplo, uma metassuperfície de grafeno é projetada para combinar a funcionalidade de geração de ondas de vórtice e direcionamento das ondas. O grafeno é um material espesso atômico bidimensional, que pode ajustar dinamicamente a condição de fase aplicando tensões de porta externa. Seus parâmetros são examinados para calibrar o comportamento reflexivo de uma única célula de grafeno e obter cobertura de 360 ^∘ mudança de fase. Uma metassuperfície de grafeno consistindo de células unitárias de 32 × 32 é projetada para realizar reflexão anômala e gerar onda de vórtice THz simultaneamente. Os resultados da simulação mostram que uma onda de vórtice com l =1 é gerado e dirigido. O grafeno exibe muitos comportamentos extraordinários em regime de terahertz, como suporte a SPP, alta eficiência e sintonia; portanto, é um candidato promissor em tecnologia terahertz. Esta pesquisa investiga a abordagem para combinar as funcionalidades de diferentes metassuperfícies implementadas pelo grafeno, que abre a porta de metassuperfícies multifuncionais controladas dinamicamente em regime de terahertz.

Disponibilidade de dados e materiais

Os conjuntos de dados gerados durante e / ou analisados durante o estudo atual estão disponíveis nos autores correspondentes mediante solicitação razoável.

Abreviações

OAM:: Momento angular orbital
SPP:: Plasmon polariton de superfície

Otimização de contatos ôhmicos para nanowires de p-GaAs Matrizes de nanofolha de TiO2 com nanopartículas de SnS2 e CoOx em camadas para divisão fotoeletroquímica eficiente da água

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias