Transmissão unidirecional dependente de pseudospin em cristais plasmônicos topológicos baseados em grafeno

Resumo

Originário da investigação dos estados da matéria condensada, o conceito de efeito Hall quântico e efeito Hall de spin quântico (QSHE) foi recentemente expandido para outro campo da física e engenharia, por exemplo, fotônica e fonônica, dando origem a modos de borda notavelmente não convencionais imunes a espalhamento. Aqui, apresentamos o análogo plasmônico de QSHE em cristal plasmônico de grafeno (GPC) em frequências de infravermelho médio. A inversão de banda ocorre ao deformar os GPCs da rede em favo de mel, o que ainda leva a lacunas de banda topológicas e recursos de pseudoespinha dos estados de borda. Sobrepondo as lacunas de banda com diferentes topologias, simulamos numericamente a propagação unilateral dependente de pseudo-rotação de estados de borda. O GPC projetado pode encontrar aplicações potenciais nas áreas de plasmônica topológica e desencadear a exploração da técnica de multiplexação de pseudospin em circuitos integrados nanofotônicos de alta densidade.

Histórico

Isoladores topológicos fotônicos [1,2,3,4], materiais ópticos de uma fase topológica não trivial que proíbem a transmissão de luz em seus interiores, mas permitem a propagação ao longo de suas bordas, foram estudados intensamente após a descoberta do efeito Hall quântico (QHE) em condensado importam. Uma manifestação chave da física topológica é a presença de estados de borda que são robustos contra defeitos estruturais ou distúrbios locais. Particularmente, utilizando a correspondência bulk-edge [5, 6], pode-se investigar diferentes fases topológicas sondando estados de borda ou invariantes topológicos de borda. Nos últimos anos, estados de borda topológicos foram previstos e observados em muitos sistemas de gap topológico fotônico, como cristais fotônicos giromagnéticos [7,8,9], isoladores topológicos fotônicos de base bi-anisotrópica [10, 11], redes de guias de ondas acopladas [12, 13], e redes fotônicas Floquet [14, 15], onde vários mecanismos físicos são propostos para fornecer proteção topológica. Notavelmente, um cone de Dirac duplo foi aberto para obter uma lacuna de banda topologicamente não trivial em um cristal fotônico de rede em favo de mel bem conhecido que preserva simetria de reversão de tempo pseudo, que dá origem a transmissão unidirecional dependente de pseudo-pino de estados de borda [16, 17]. Além dos sistemas fotônicos, os estados de borda dependentes de pseudospin em sistemas fonônicos têm sido explorados [18,19,20]. No entanto, a analogia nas nanoestruturas plasmônicas ainda não foi relatada, o que se deve à enorme perda ôhmica dos plasmons que se propagam ao longo dos materiais plasmônicos tradicionais como Au e Ag.

Polaritons de plasma de superfície (SPPs) [21], excitações elementares acopladas por fótons e oscilações de elétrons livres em uma interface entre um metal e um dielétrico, são considerados um mecanismo físico promissor para contornar a limitação de difração e para avançar a miniaturização dos dispositivos . Iurov et al. explorou a retroação e hibridização dos modos de plasmon e encontrou a polarização óptica induzida por elétrons de Dirac no grafeno [22]. Memmi et al. relataram o forte acoplamento entre SPPs e vibrações moleculares [23]. Embora metais nobres comumente usados, como ouro e prata, exibam propriedades plasmônicas principalmente na região visível e infravermelho próximo do espectro, o grafeno surgiu recentemente como uma alternativa promissora que é capaz de estender o campo da plasmônica para infravermelho e terahertz (THz). comprimentos de onda. Mais importante, em contraste com os metais nobres, plasmons de grafeno podem ser ajustados dinamicamente via polarização eletrostática [24, 25], o que permite uma nova geração de dispositivos plasmônicos reconfiguráveis. Além disso, os SPPs animados com grafeno de alta qualidade podem atingir tempos de relaxação intrínseca notavelmente longos e fornecer níveis sem precedentes de confinamento de campo [26]. Essas propriedades extraordinárias tornam o grafeno um candidato ideal para os componentes plasmônicos topológicos totalmente integrados. Muito recentemente, Jin et al. perceberam os plasmons de borda unilateral protegidos topologicamente em uma monocamada periodicamente padronizada de grafeno, onde a topologia da banda de plasmons de grafeno sob um campo magnético de quebra de reversão de tempo foi estudada em detalhes [27]. E Pan et al. demonstraram o comportamento não recíproco substancial nas junções da super-rede sob campos magnéticos estáticos moderados, levando ao surgimento de estados de borda protegidos topologicamente e modos de bulk localizados [28].

Neste trabalho, exploramos teoricamente as propriedades topológicas de cristais plasmônicos de grafeno bidimensionais (2D) (GPCs) construídos por nanodiscos de grafeno organizados periodicamente. Os cones de Dirac nos cantos da zona de Brillouin (BZ) são dobrados em um cone de Dirac duplo no centro de BZ, utilizando o mecanismo de dobramento de zona. A fim de obter lacunas de banda topológicas, tomamos mais deformações na rede em favo de mel. Ao encolher ou expandir os nanodiscos de grafeno, o cone de Dirac duplo é aberto e a inversão de banda ocorre entre os modos dipolo e quadrupolo pseudospin, o que ainda leva à transição de fase topológica entre os estados não triviais e triviais. Além disso, a propagação unilateral de estados de borda é numericamente simulada ao longo de uma interface construída pelos GPCs triviais e não triviais, o que demonstra ainda mais as características do pseudospin e a robustez topológica de nossos cristais plasmônicos projetados.

Métodos

Investigamos a topologia de banda de SPPs em um cristal plasmônico 2D de uma matriz de nanodiscos de grafeno dispostos periodicamente cercados pela mesma folha de grafeno com potencial químico diferente, conforme mostrado na Fig. 1a. A constante de rede a =40 nm, μ _c1 , e r são o potencial químico e os raios dos nanodiscos de grafeno; μ _c2 denota o potencial químico do grafeno circundante. Resolvendo as equações de Maxwells com as condições de contorno, obtemos a relação de dispersão para os modos SPP polarizados magnéticos transversais (TM) suportados na camada de grafeno circundada por ar e sílica [29]:
$$ \ frac {\ varepsilon _ {\ mathrm {Ar}}} {\ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _ {Ar}}} + \ frac {\ varepsilon_ {Si {O } _2}} {\ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _ {{\ mathrm {SiO}} _ 2}}} =\ frac {\ sigma_g} {i {\ omega \ varepsilon } _0}. $$ (1)

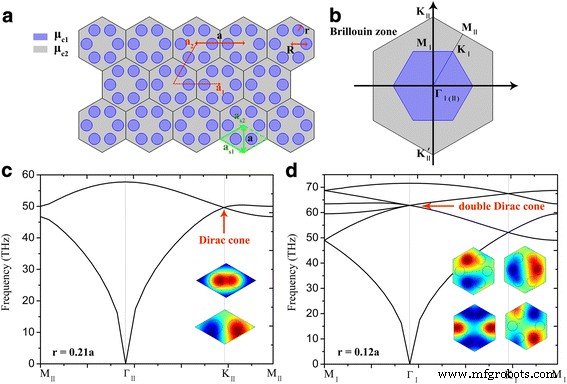
a Esquemas dos GPCs 2D. b As zonas de Brillouin. c Estrutura de banda da rede baseada na célula unitária rômbica primitiva indicada com linhas tracejadas verdes, as inserções representam as distribuições do campo elétrico próprio do ponto de Dirac. d Estrutura de banda da rede baseada na célula unitária hexagonal, os insets representam as distribuições do campo elétrico próprio do ponto de Dirac duplo. Os outros parâmetros são definidos como μ _c1 =0,3 eV, μ _c2 =0,6 eV, τ =1 ps, a constante de rede a =40 nm

Aqui, ε ₀ é a permissividade do vácuo do espaço livre, k ₀ =2π / λ é o número da onda no espaço livre, e λ é o comprimento de onda operacional no vácuo. Na região do infravermelho médio, as constantes dielétricas de ar e sílica correspondentes a super e substratos são assumidas como ε _Ar =1 e ε _SiO2 =3,9 respectivamente [30]. No regime não retardado, onde β » k ₀ , a Eq. (3) pode ser simplificado para [31].
$$ \ beta ={\ varepsilon} _0 \ frac {\ varepsilon _ {\ mathrm {Air}} + {\ varepsilon} _ {{\ mathrm {SiO}} _ 2}} {2} \ frac {2 i \ omega} {\ sigma _ {\ mathrm {g}}}, $$ (2)
onde β é a constante de propagação SPPs na camada de grafeno, e o índice de refração efetivo n _eff do modo SPP pode ser derivado de n _eff = β / k ₀ . σ _g é a condutividade da superfície do grafeno composta pelas contribuições intrabanda e interbanda, ou seja, σ _g = σ _intra + σ _inter [29, 30]. A condutividade intrabanda σ _intra correspondente ao processo de espalhamento elétron-fóton intrabanda é dado por
$$ {\ sigma} _ {\ mathrm {intra}} =\ frac {ie ^ 2 {k} _BT} {\ pi {\ mathrm {\ hslash}} ^ 2 \ left (\ omega + i / \ tau \ direita)} \ left [\ frac {\ mu _ {\ mathrm {c}}} {k_BT} +2 \ ln \ left (1+ \ exp \ left (- \ frac {\ mu _ {\ mathrm {c}}} {k_BT} \ right) \ right) \ right], $$ (3)
onde μ _c é o potencial químico relacionado à densidade do elétron, e é a carga do elétron, ω é a frequência angular do plasmon, ℏ e k _B são a constante de Planck reduzida e a constante de Boltzmann, respectivamente, T é a temperatura, e τ representa o tempo de relaxamento do momento do elétron devido ao espalhamento do portador de carga. Para ℏω » k _B T e | μ _c | » k _B T , a condutividade entre bandas σ _inter correspondentes às transições de elétrons entre bandas podem ser expressas aproximadamente como
$$ {\ sigma} _ {\ mathrm {inter}} =\ frac {ie ^ 2} {4 \ pi \ mathrm {\ hslash}} \ ln \ left [\ frac {2 \ mid {\ mu} _ { \ mathrm {c}} \ mid - \ mathrm {\ hslash} \ left (\ omega + i / \ tau \ right)} {2 \ mid {\ mu} _ {\ mathrm {c}} \ mid + \ mathrm {\ hslash} \ left (\ omega + i / \ tau \ right)} \ right]. $$ (4)

Resultados e discussão

As estruturas de banda de energia dos cristais plasmônicos propostos são obtidas empregando o método dos elementos finitos (FEM) com base no software comercialmente disponível COMSOL Multiphysics. Na Fig. 1a, notamos que ambas as células unitárias rômbicas de dois nanodiscos de grafeno (losango verde tracejada definido pelos vetores a _s1 e a _s2 ) e a célula unitária hexagonal de seis nanodiscos de grafeno (com vetores de rede a ₁ e a ₂ ) podem formar os cristais plasmônicos de estrutura em favo de mel. A Figura 1b apresenta os BZs para as células unitárias rômbicas e hexagonais, com as zonas irredutíveis de M _II - Γ _II - K _II - M _II e M _I - Γ _I - K _I - M _I respectivamente. Observe que a célula unitária hexagonal é três vezes maior do que a primitiva rômbica. Portanto, o primeiro BZ da célula unitária rômbica primitiva é três vezes maior do que o hexagonal (região azul na Fig. 1b). Ao tomar uma célula unitária rômbica primitiva, este cristal plasmônico exibe dispersão de cone de Dirac em K _II e K _II `aponta nos cantos BZ como mostrado na Fig. 1c. As inserções na Fig. 1c mostram as distribuições do campo elétrico próprio dos dois estados degenerados no ponto de Dirac. Semelhante aos pseudo-spins em sistemas fotônicos clássicos e acústicos [17, 19, 20], a fim de imitar o análogo dos pseudo-spins no sistema plasmônico, o grau de liberdade deve ser aumentado para dois estados. Assim, são necessários cones de Dirac duplos degenerados quatro vezes na estrutura de banda plasmónica. Ao empregar o mecanismo de dobramento de zona [18], os cones de Dirac em K _II e K _II `as pontas são dobradas em um cone de Dirac duplo em Γ ponto no centro BZ ao tirar a célula de unidade hexagonal maior (como mostrado na Fig. 1d). As inserções na Fig. 1d mostram os auto-estados quádruplos degenerados com modos dipolo e quadrupolo. Os parâmetros relativos que usamos são μ _c1 =0,3 eV, μ _c2 =0,6 eV e τ =1 ps, que são moderadamente escolhidos de pesquisas anteriores para o grafeno prático [32, 33].

Os cones de Dirac duplos degenerados quádruplos compostos por dois modos dipolares e dois quadrupolares estão associados a duas representações irredutíveis 2D de um C _6v grupo de pontos, a saber, E ₁ modos de paridade espacial ímpar e E ₂ modos de paridade espacial uniforme. Seguindo a notação convencional amplamente adotada na mecânica quântica [34], podemos classificar esses modos como p _x / p _y e d _x2-y2 / d _xy modos de acordo com seus próprios E _z distribuições de campo mostradas na Fig. 2. Em seguida, a fim de abrir um gap topológico não trivial no Γ ponto, fazemos modificações adicionais (ou seja, deformar a estrutura do favo de mel de a / R =3) na célula unitária hexagonal para quebrar a simetria. Ao reduzir os nanodiscos de grafeno para a / R =3,2, o cone de Dirac duplo degenerado quádruplo se divide em dois estados degenerados duas vezes e uma lacuna de banda em massa aberta de 62,1 para 63,5 THz como mostrado na Fig. 2a. O E _z campos das bandas inferiores têm um par de modos dipolo exibindo p _± caracteres, enquanto as bandas superiores têm um par de modos quadrupolo exibindo d _± personagens em torno do Γ ponto, o que é consistente com a teoria fotônica clássica de que os modos dipolo devem exibir frequência mais baixa do que os modos quadrupolo de ordem superior. No entanto, uma inversão de banda ocorre ao expandir os nanodiscos de grafeno para a / R =2,9, isto é, os modos dipolo sobem acima dos modos quadrupolo, o que provoca o gap não trivial topológico de 62,4 a 63,3 THz, como mostrado na Fig. 2c. A Figura 2d, e ilustra o processo de transição topológica entre p _± e d _± estados, e os campos magnéticos no plano associados a p _± e d _± são marcados com setas brancas. Os momentos angulares da função de onda de E _z campos p _± =( p _x ± i p _y ) / \ (\ sqrt {2} \) e d _± =( d _x2-y2 ± i d _xy ) / \ (\ sqrt {2} \) constitui ainda a pseudospin nos cristais plasmônicos presentes [17, 18].

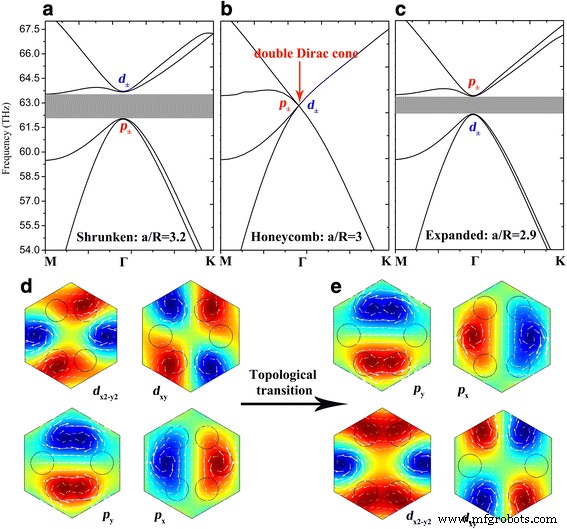
Estruturas de banda dos GPCs com a a / R =3,2, b a / R =3 e c a / R =2,9. d , e O E _z distribuições de campo de modos dipolo e modos quadrupolo do p _± e d _± estados em a e c respectivamente. As setas brancas apresentam o campo magnético no plano associado a E _z campo

Para explorar ainda mais a propriedade topológica das lacunas de banda mostradas na Fig. 2a, c, ela é geralmente relacionada a uma descrição hamiltoniana efetiva e números topológicos. Aplicando a teoria de perturbação \ (\ overset {\ rightharpoonup} {k} \ cdot \ overset {\ rightharpoonup} {p} \), o Hamiltoniano efetivo H _eff ( k ) em torno do Γ apontar com base em [ p ₊ , d ₊ , p _- , d _- ] pode ser expresso como [17, 35].
$$ {H} ^ {\ mathrm {eff}} (k) =\ left [\ begin {array} {cccc} M + {Bk} ^ 2 &{Ak} _ {+} &0 &0 \\ {} {A } ^ {\ ast} {k} _ {-} &-M- {Bk} ^ 2 &0 &0 \\ {} 0 &0 &M + {Bk} ^ 2 &{Ak} _ {-} \\ {} 0 &0 &{ A} ^ {\ ast} {k} _ {+} &-M- {Bk} ^ 2 \ end {array} \ right], $$ (5)
onde k _± = k _x ± i k _y e A vem de elementos fora da diagonal do termo de perturbação de primeira ordem \ ({M} _ {\ alpha \ beta} =\ left \ langle {\ Gamma} _ {\ alpha} \ left | \ overset {\ rightharpoonup} {k } \ cdot \ overset {\ rightharpoonup} {p} \ right | {\ Gamma} _ {\ beta} \ right \ rangle \) com α =1, 2 e β =3, 4. O hamiltoniano efetivo H _eff ( k ) assume uma forma semelhante ao modelo Bernevig-Hughes-Zhang (BHZ) para o sistema de poço quântico CdTe / HgTe / CdTe [36], implicando um gap topológico quando ocorre a inversão de banda. Com base no hamiltoniano expresso na Eq. (5), podemos avaliar os números de spin Chern dos cristais plasmônicos topológicos como [36].
$$ {C} _ {\ pm} =\ pm \ frac {1} {2} \ left [\ operatorname {sgn} (M) + \ operatorname {sgn} \ left (-B \ right) \ right]. $$ (6)
Aqui, M =( E _p - E _d ) / 2 é a diferença de frequência entre E ₂ e E ₁ representações no Γ ponto. B é determinado pelos elementos diagonais do termo de perturbação de segunda ordem e é tipicamente negativo [19]. Assim, C _± =0 é obtido quando há uma ordem de banda normal, conforme exibido na Fig. 2a. E concluímos que o gap aberto é trivial. No entanto, M torna-se positivo quando ocorre inversão de banda. Portanto, C _± =± 1 é obtido simplesmente, e a lacuna na Fig. 2c não é trivial.

Ao sobrepor as lacunas de banda com diferentes topologias (isto é, topológico trivial e topológico não trivial), pode-se criar estados de borda que são espacialmente confinados em torno da interface entre dois cristais plasmônicos. Aqui, consideramos uma fita de cristal plasmônico topologicamente não trivial (com estrutura de banda mostrada na Fig. 2c) com suas duas bordas revestidas por dois cristais plasmônicos topologicamente triviais (com estrutura de banda mostrada na Fig. 2a) na mesma janela de frequência. As duas regiões triviais evitam que possíveis estados de borda vazem para o espaço livre. Na Fig. 3a, apresentamos as estruturas de banda projetadas calculadas ao longo do Γ Direção K para tal fita, onde uma lacuna de banda em massa é abrangida por estados de borda topológica adicionais, conforme indicado pelas curvas vermelhas degeneradas duplas. A Fig. 3b representa as distribuições do campo elétrico confinado ao redor da interface construída por dois cristais distintos, correspondendo aos pontos A (com k _x =- 0,05π / a ) e B (com kx =0,05π / a ) marcado na Fig. 3a. As características de pseudo spin-up e spin-down são evidenciadas por vórtices de fase no sentido anti-horário e horário, conforme ilustrado no painel direito da Fig. 3b.

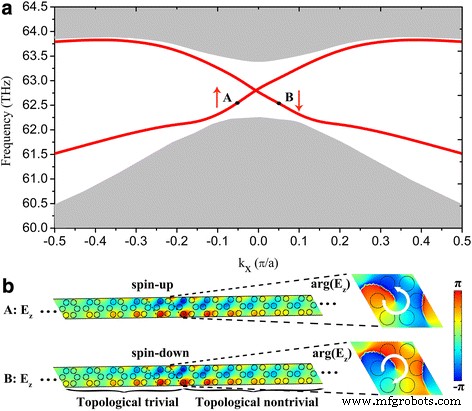
a Estrutura de banda projetada para uma supercélula composta por 16 células unitárias não triviais revestidas por 12 células unitárias triviais em ambos os lados. b Distribuições de campo elétrico em torno da interface entre os cristais plasmônicos triviais e não triviais nos pontos A e B, ou seja, em k _x =- 0,05π / a e 0,05π / a respectivamente

A transmissão unidirecional dependente de pseudospin de estados de borda também é demonstrada em um 20 a finito × 18 a rede construída pelos cristais triviais e não triviais. Como mostrado na Fig. 4a, b, propagação unilateral da onda SPP para a direção esquerda (direita) quando excitada por uma fonte pseudo spin-up (spin-down) S ₊ ( S _- ) de polarização circular no sentido anti-horário (sentido horário) do campo magnético no plano. Uma das características mais distintivas dos estados de borda topológicos é que eles são robustos contra perturbações / imperfeições. Para verificar esta robustez, construímos curvas agudas como mostrado na Fig. 4c, onde a transmissão unidirecional da onda SPP é excitada por uma fonte pseudo spin-down S _- . A onda SPP desapareceu eventualmente após uma longa distância de viagem ao longo das curvas acentuadas devido à perda intrínseca de material de grafeno. Para confirmar ainda mais essa transmissão topológica, também exibimos a distribuição da intensidade do campo elétrico, ignorando a perda intrínseca de grafeno para comparação. Como pode ser visto na Fig. 4d, a onda SPP segue a rota projetada e mantém a propagação unilateral com pouco retroespalhamento.

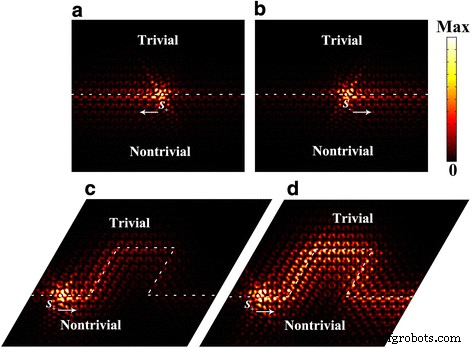
a Esquerda e b estados de borda unilateral à direita excitados pelo campo magnético no plano com uma diferença de fase π / 2:\ ({S} _ {\ pm} ={H} _0 \ left (\ overset {\ rightharpoonup} {x} \ mp i \ overset {\ rightharpoonup} {y} \ right) \). c Estados de borda topológicos viajando ao longo de curvas acentuadas. d A distribuição da intensidade do campo elétrico da transmissão topológica unilateral sem considerar a perda intrínseca de material de grafeno

Conclusões

Em resumo, investigamos sistematicamente as topologias de banda dos GPCs construídos por nanodiscos de grafeno periodicamente padronizados. Ao empregar o mecanismo de dobramento de zona, os cones Dirac no canto BZ são dobrados em um cone Dirac duplo no centro BZ. Além disso, lacunas de banda topológicas são realizadas deformando os GPCs de rede em favo de mel. Com base no hamiltoniano efetivo derivado da teoria de perturbação \ (\ overset {\ rightharpoonup} {k} \ cdot \ overset {\ rightharpoonup} {p} \), os números de spin de Chern são avaliados. As características de pseudospin, evidenciadas por vórtices de fase no sentido anti-horário e horário, são usadas com sucesso para realizar a transmissão unidirecional de estados de borda ao longo de uma interface construída por dois cristais plasmônicos topológicos triviais e não triviais. O GPC projetado fornece um novo caminho para a pesquisa de fenômenos topológicos e pode encontrar aplicações potenciais nos campos da plasmônica topológica. Também pode desencadear a exploração da plasmonics pseudospin e da técnica de multiplexação pseudospin em circuitos integrados nanofotônicos de alta densidade.

Abreviações

BHZ:: Bernevig-Hughes-Zhang
BZ:: Zona de Brillouin
FEM:: Método do elemento finito
GPC:: Cristal plasmônico de grafeno
QHE:: Efeito Quantum Hall
QSHE:: Efeito Hall de rotação quântica
SPPs:: Polaritons de plasmon de superfície

Nanocristal Sb2O3 dopado com S:um catalisador de luz visível eficiente para degradação orgânica Estudo comparativo das propriedades eletroquímicas, biomédicas e térmicas de nanomateriais naturais e sintéticos

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias