Mudança na condutividade da superfície de cristais p-Si deformados elasticamente irradiados por raios-X

Resumo

Alterações na condutividade de monocristais de p-Si irradiados e não irradiados sob a influência de estresse mecânico uniaxial elástico foram investigadas neste trabalho. Uma expressão analítica foi sugerida para descrever a dependência da condutividade superficial em função do estresse mecânico e da dose de irradiação de raios-X. Foi mostrado que nanopartículas angulares na superfície do silício “solar” afetam as mudanças de eletrocondutividade sob estresse mecânico. Foi estabelecido que a irradiação de raios X causa a geração de defeitos pontuais no silício. Esses defeitos suprimem o movimento das luxações. Foi mostrado que a resistividade de amostras previamente irradiadas de silício “eletrônico” é apenas ligeiramente sensível à influência da compressão uniaxial em certa taxa de deformação.

Histórico

O uso generalizado de dispositivos semicondutores no campo das tecnologias eletrônicas modernas requer a investigação de novos materiais semicondutores que possuem alta estabilidade sob a influência externa, como irradiação de raios-X e deformação mecânica. Hoje em dia, o silício é usado ativamente em detectores de alta sensibilidade e outros sensores semicondutores que operam nos campos de radiação [1].

A maioria dos artigos é dedicada ao impacto da deformação plástica na condutividade do n-Si [2, 3]. É por isso que o impacto da deformação elástica nas propriedades dos cristais de p-Si ainda é considerado uma tarefa científica importante. A redistribuição da concentração de carreadores e impurezas em cristais deformados é frequentemente caracterizada pela presença de deslocamentos que são captadores efetivos de defeitos, especialmente na superfície do cristal [4, 5]. Sabe-se [3, 6] que a excitação dos subsistemas eletrônicos de cristal também é acompanhada pelas correspondentes mudanças na mobilidade de deslocamento. A excitação dos subsistemas eletrônicos pode ser resultado de influências externas, como radiação e campo eletrostático. Uma característica dos deslocamentos em cristais de silício é a presença de defeitos pontuais (nuvem de Cottrell) com alta concentração ao redor dos deslocamentos.

A superfície dos cristais é a mais sensível à radiação ionizante. É por isso que a investigação de processos induzidos por radiação nas camadas superficiais dos cristais de silício ainda é considerada relevante. A superfície com os contatos de Al depositados é um getter eficaz para os defeitos estruturais [5,6,7]. Debaixo do filme metálico depositado, as tensões mecânicas aparecem devido a inconsistências nos parâmetros de rede do filme e do semicondutor [5, 7]. Essas tensões estimulam os processos de obtenção de defeitos (átomos de impureza, átomos de silício intersticiais e vazios) na camada de contato.

Métodos

Monocristais de silício de condutividade do tipo p, cultivados pelo método de Czochralski ( ρ =10–20 Ω cm), foram usados no artigo de pesquisa. Esses monocristais são de dois tipos:(1) silício para eletrônicos - os chamados monocristais livres de deslocamento (ou eletrônicos) na superfície (111) dos quais, a concentração de poços de corrosão triangular não excede 10 ² cm ⁻² (Figs. 1a e 2), e (2) monocristais "solares" de silício na superfície (111) dos quais, os defeitos na forma de pirâmides de 4 angulares (Fig. 1b) foram descobertos devido a um grande concentração de carbono de fundo (≈5 × 10 ¹⁶ cm ⁻³ ) e oxigênio (≈1,8 × 10 ¹⁸ cm ⁻³ ) impurezas. As pirâmides de quatro ângulos estão localizadas da mesma maneira. O tamanho da base da pirâmide é de 10 nm a 10 μm.

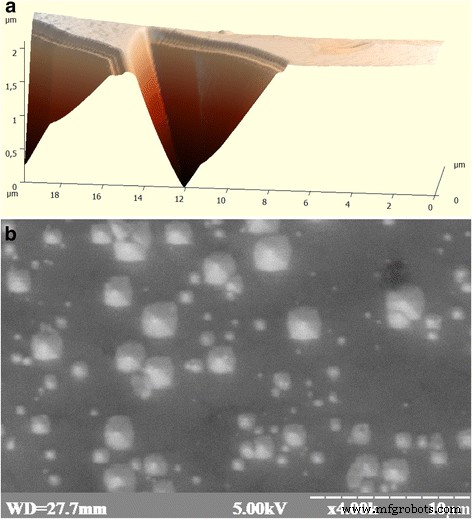
O aspecto da superfície das amostras experimentais: a aparecimento de poços de corrosão por deslocamento na superfície do cristal de p-Si obtido no campo do microscópio de força atômica e b aparecimento de superfície submicroscópica (111) de cristais solares

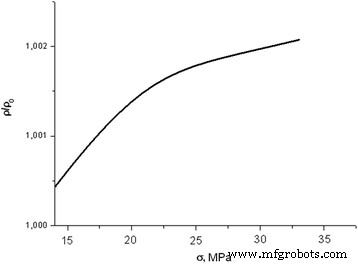
Dependência da resistência longitudinal da amostra livre de deslocamento primário durante a deformação elástica com a taxa de deformação de 8 μm / min

Foi demonstrado [8, 9] que na formação dos aglomerados, aos quais correspondem orifícios piramidais de ataque 4-angulares podem participar camadas de óxido de silício, defeitos pontuais e camadas com diferentes estados estruturais de silício, particularmente silício alfa.

Amostras experimentais obtiveram dimensões de 4 × 3,7 × 7,6 mm após lixamento e polimento químico. Contatos ôhmicos na forma de duas tiras com largura de 1,5 mm nas extremidades das superfícies da amostra (111) foram criados por evaporação térmica de alumínio no vácuo (10 ⁻⁴ Pa) aquecido a amostra de 593 K. A medição da condutividade elétrica foi conduzida em um criostato a vácuo com pressão de gás residual 10 ⁻³ Pa na aplicação de compressão uniaxial às extremidades (em direção a [\ (11 \ overline {2} \)]) com uma potência de 15 a 40 MPa e uma taxa de deformação de 8 ou 32 μm / min. As amostras foram irradiadas com uma gama completa de radiação X ( W -anodo, 50 kV, 10 mA), em ambos os lados, nos quais foram revestidos os contatos de alumínio. A distância entre a fonte de raios X e os cristais era mínima (1–2 mm). Verificou-se que a dose absorvida aumentava 130 Gy a cada 30 min. No trabalho, primeiramente irradiamos as amostras experimentais e, em seguida, medimos a resistência no processo de deformação.

Resultados e discussão

O resultado da pesquisa sobre a mudança da condutividade mecânica induzida ao longo da direção de deformação ( ρ ( σ )) de amostras "livres de deslocamento" de condutividade do tipo p sob a influência de tensão uniaxial ( σ ) é mostrado na Fig. 2. O aumento da carga de 0 para 40 MPa (na taxa de deformação de 8 μm / min) dura 45 min.

No processo de deformação, a resistência das amostras livres de deslocamento aumenta ligeiramente. Deve-se notar que, no caso de cristais não irradiados, a mudança da taxa de deformação praticamente não teve efeito na visão geral das dependências ρ ( σ ) [10, 11]. Dependências semelhantes foram obtidas para amostras irradiadas (Fig. 3). Observou-se aumento da resistência após a ação da irradiação X. No entanto, a natureza da dependência ρ ( σ ) foi observado ser um pouco diferente do que para amostras não irradiadas.

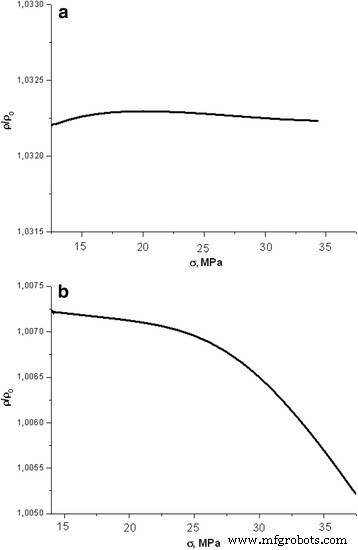
Dependência da resistência longitudinal do irradiado ( D =130 Gy) amostra livre de deslocamento de silício durante a deformação elástica com uma força de compressão crescente a uma velocidade de 8 μm / min ( a ) e 32 μm / min ( b )

Pode-se observar que a resistência permanece virtualmente imutável (Fig. 3a) durante a compressão a uma velocidade de 8 μm / min devido ao efeito da irradiação X. Os gráficos de dependências das amostras expostas a 260 e 480 Gy tiveram aparência semelhante. Foi demonstrado em estudos anteriores [11] que a resistência estava aumentando proporcionalmente à raiz quadrada da dose absorvida durante o processo de irradiação.

Um aumento de quatro vezes na taxa de compressão (de 8 para 32 μm / min) leva às mudanças na natureza da dependência da resistividade na carga (Fig. 3b). Há uma pequena queda (<0,2%) na resistência das amostras irradiadas no processo de compressão. Deve-se notar que todas as medições nas mudanças de condutividade foram realizadas com um alto grau de precisão (± 0,045%) de forma que foi possível analisar corretamente pequenas mudanças na resistividade no experimento.

Deve-se notar que a dependência, mostrada na Fig. 3, foi recebida 7 dias após a medição das mudanças na resistência longitudinal ( D =130 Gy) de amostras livres de deslocamento a uma velocidade de 8 μm / min (Fig. 3a). Durante o período de tempo determinado, a resistência quase voltou ao seu valor original, ou seja, o valor da resistência, que foi observado após a irradiação e aplicação de tensões mecânicas.

Estudos semelhantes sobre a medição da dependência da resistência na ação da compressão elástica e após a exposição à radiação também foram conduzidos (Fig. 4) para amostras experimentais baseadas em “silício solar” de condutividade tipo p, às quais são inerentes pirâmides 4 angulares em a superfície (111).

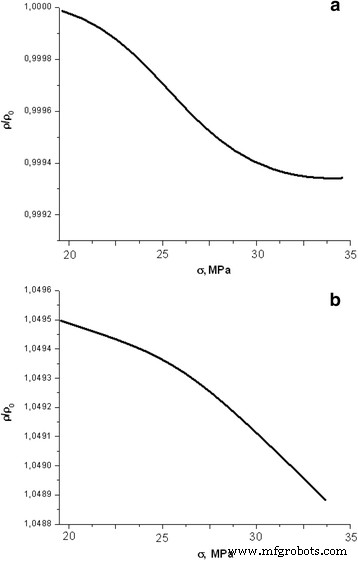
Dependência da resistência longitudinal do silício solar durante a deformação elástica com uma crescente resistência à compressão: a D =0 Gy, velocidade de compressão 32 μm / min; b D =130 Gy, velocidade de compressão de 8 μm / min

Em primeiro lugar, verificou-se que a natureza da variação da resistência do silício “solar” do tipo p-Si no tamanho da tensão mecânica é independente da velocidade de compressão. Uma característica semelhante foi observada em amostras irradiadas e não irradiadas. A dependência da resistência longitudinal na tensão mecânica muda em um valor relativamente pequeno (<0,5%), e diminui ligeiramente com o aumento da carga (Fig. 4a).

A irradiação de amostras experimentais com raios-X (480 Gy) não afeta virtualmente a natureza geral da mudança na resistência longitudinal do silício “solar” durante a deformação elástica (Fig. 4b). Já nas amostras eletrônicas, a resistência é proporcional à raiz quadrada da dose absorvida [11]. Durante o estresse mecânico, a resistividade diminui em um valor muito pequeno (± 0,1%).

Como foi mostrado em nossos estudos anteriores [12, 13], o filme dielétrico SiO ₂ tem uma carga positiva. Portanto, a camada de superfície de carga espacial se esgota em orifícios (com alta resistência) e com uma espessura w (Fig. 5) é criado em silício. Quanto mais próximo o Si-SiO ₂ para a interface, menos furos existem.

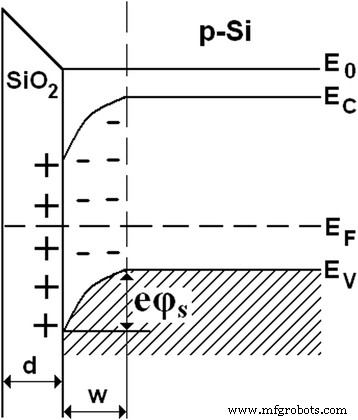
Distorção das bandas de energia no condutor tipo p sob carga positiva fornecida na interface do semicondutor-isolante

A concentração de orifícios na camada superficial de silício e, conseqüentemente, sua condutividade muda no caso de alteração do potencial de superfície ( φ _S ) Vamos considerar uma placa quadrada plana (Fig. 6). Deixe a corrente fluir paralelamente ao plano da placa na direção de uma de suas bordas.

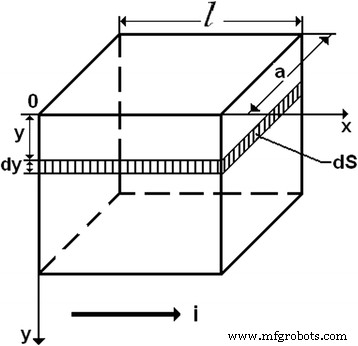
Cálculos de condutividade

Foi retirada uma fina camada paralela com espessura dy e área da seção transversal dS [14] a alguma distância ( y ) da superfície. Esta camada pode ser considerada semicondutora homogênea, cuja resistência pode ser determinada de acordo com a seguinte fórmula:
$$ d R =\ rho \ frac {l} {dS}, $$ (1) $$ d S =a d y. $$ (2)
Como o prato é quadrado ( l = a ), a condutividade da camada é
$$ d \ lambda =\ frac {1} {dR} =\ sigma d y, $$ (3)
onde \ (\ sigma =\ frac {1} {\ rho} \) é a condutividade elétrica da camada com dy espessura em y distância da superfície. Para um semicondutor do tipo p, a condutividade pode ser escrita como \ (\ sigma \ approx e p (y) {\ mu} _p \). Então nós temos
$$ d \ lambda =e p (y) {\ mu} _p dy. $$ (4)
Vamos encontrar a condutividade total da superfície ( λ ) Você precisa integrar a última expressão no intervalo de zero a uma espessura de várias telas Debye sustentáveis ou, por exemplo, restringir a largura da região de carga espacial w :
$$ \ lambda ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} ep (y) {\ mu} _p dy =e {\ mu} _p {\ displaystyle \ underset {0} { \ overset {w} {\ int}} p (y) dy}}. $$ (5)
Em geral, a concentração de orifícios na camada superficial esgotada não depende apenas das coordenadas ( y ), mas também na tensão mecânica aplicada ( σ _meh ) É determinado por dois componentes: p ( y , σ _meh ) = p ₁ ( y ) - p ₂ ( σ _meh ), onde p ₁ ( y ) é um componente que corresponde a uma mudança na concentração do portador com a mudança da distância da superfície do semicondutor e p ₂ ( σ _meh ) é um componente que mostra o quanto a concentração de furos é reduzida devido à sua captura nos deslocamentos durante o estresse mecânico. Além disso, a mobilidade dos orifícios não é um valor constante. Depende do estresse mecânico. Portanto, a expressão para a condutividade total da superfície pode ser escrita da seguinte forma:
$$ \ lambda =e {\ mu} _p \ left ({\ sigma} _ {meh} \ right) {\ displaystyle \ underset {0} {\ overset {w} {\ int}} \ left ({p} _1 (y) - {p} _2 \ left ({\ sigma} _ {meh} \ right) \ right) dy}. $$ (6)
A mudança induzida mecanicamente na condutividade pode ser escrita da seguinte forma:
$$ \ lambda \ left ({\ sigma} _ {meh} \ right) =e {\ mu} _p \ left ({\ sigma} _ {meh} \ right) \ cdot \ Big ({\ displaystyle \ underset { 0} {\ overset {w} {\ int}} {p} _1 (y) dy - {\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _2 \ left ({\ sigma} _ {meh} \ right) dy} \ Big) =e {\ mu} _p \ left ({\ sigma} _ {meh} \ right) \ cdot \ left \ {{\ beta} _1 - {\ beta } _2 \ left ({\ sigma} _ {meh} \ right) \ right \}}, $$ (7)
onde \ ({\ beta} _1 ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 (y) dy; \ kern1em {\ beta} _2 \ left ({\ sigma } _ {meh} \ right) ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _2 \ left ({\ sigma} _ {meh} \ right) dy}} ={p} _2 \ left ({\ sigma} _ {meh} \ right) {\ displaystyle \ underset {0} {\ overset {w} {\ int}} dy =} w \ cdot {p} _2 \ left ( {\ sigma} _ {meh} \ right) \).

Deve-se notar que, uma vez que p ₁ ( y ) e p ₂ ( σ _meh ) também dependem do efeito de irradiação, os fatores β ₁ , β ₂ e μ _p dependem da dose de radiação-X. Portanto, a fórmula para a condutividade da superfície antes de ( λ ( σ _meh , 0 )) e depois ( λ ( σ _meh , D )) a irradiação pode ser escrita da seguinte forma:
$$ \ lambda \ left ({\ sigma} _ {meh}, 0 \ right) =e {\ mu} _p \ left ({\ sigma} _ {meh}, 0 \ right) \ cdot \ Big ({\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 \ left (y, 0 \ right) dy- w \ cdot {p} _2 \ left ({\ sigma} _ {meh} , 0 \ right) \ Big) =e {\ mu} _p \ left ({\ sigma} _ {meh}, 0 \ right) \ cdot \ left \ {{\ beta} _1 (0) - {\ beta} _2 \ left ({\ sigma} _ {meh}, 0 \ right) \ right \}}. $$ (8) $$ \ lambda \ left ({\ sigma} _ {meh}, D \ right) =e {\ mu} _p \ left ({\ sigma} _ {meh}, D \ right) \ cdot \ Big ({\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 \ left (y, D \ right) dy- w \ cdot {p} _2 \ left ({\ sigma } _ {meh}, D \ right) \ Big) =e {\ mu} _p \ left ({\ sigma} _ {meh}, D \ right) \ cdot \ left \ {{\ beta} _1 (D) - {\ beta} _2 \ left ({\ sigma} _ {meh}, D \ right) \ right \}}. $$ (9)
Se a amostra tiver uma forma retangular com um comprimento ( l ) e largura ( a ), podemos escrever a fórmula final para a condutividade total da superfície da seguinte forma:
$$ \ lambda \ left ({\ sigma} _ {meh}, D \ right) =\ frac {a} {l} e {\ mu} _p \ left ({\ sigma} _ {meh}, D \ right ) \ left \ {{\ beta} _1 (D) - {\ beta} _2 \ left ({\ sigma} _ {meh}, D \ right) \ right \}, $$ (10)
Onde
$$ {\ beta} _1 (D) ={\ displaystyle \ underset {0} {\ overset {w} {\ int}} {p} _1 \ left (y, D \ right) dy, \ kern1em} {\ beta} _2 \ left ({\ sigma} _ {meh}, D \ right) =w \ cdot {p} _2 \ left ({\ sigma} _ {meh}, D \ right). $$ (11)
A mudança da condutividade da superfície de cristais de p-Si irradiados sob a influência do estresse mecânico é principalmente determinada pela mudança de três parâmetros: β ₁ , β ₂ e μ _p .

De acordo com nossos estudos anteriores, [10,11,12,13], o efeito da exposição aos raios X ao silício eletrônico é acompanhado por um ligeiro aumento na carga positiva na camada superficial dielétrica de SiO ₂ . Como resultado, o fator β ₁ : β ₁ ( D )> β ₁ ( 0 ) aumenta ligeiramente. Para o silício “solar”, as dependências opostas são observadas: β ₁ ( D ) < β ₁ ( 0 )

Em relação ao fator β ₂ , suas mudanças são principalmente determinadas pela mudança de p ₂ ( σ _meh , D ) sob efeito de radiação. Essas mudanças são muito mais substanciais em comparação com a mudança do parâmetro β ₁ . A irradiação X desencadeia a geração de defeitos pontuais no silício, que atuam como travas para o movimento de deslocamento. Como resultado, após a exposição à radiação, o fator β ₂ para essas amostras diminui drasticamente (reduz o número de furos presos por deslocamento) para ambos os tipos de amostras de experimentos p-Si: β ₂ ( D ) < β ₂ ( 0 )

Em cristais não irradiados de silício “solar”, os defeitos existentes, aos quais correspondem a cavidades piramidais 4 angulares, desempenham o papel de travas para o movimento de deslocamento. Defeitos adicionais gerados por irradiação não desempenharam um papel significativo no contexto de uma forte concentração de defeitos de superfície existentes.

A mobilidade dos orifícios diminui ligeiramente durante a exposição à radiação devido ao aumento do espalhamento nos defeitos de radiação: μ _p ( D ) < μ _p ( 0 ) Por esse mecanismo pode-se explicar a diminuição confirmada experimentalmente na condutividade de amostras de silício irradiadas. Assim, uma análise das fórmulas (8) e (9) confirma o crescimento da resistência sob o aumento do valor da dose absorvida de irradiação X principalmente pela redução da mobilidade ( μ _p ( D ) < μ _p ( 0 )) e a concentração de portadores de carga gratuita - buracos ( β ₂ ( D ) < β ₂ ( 0 )).

Se considerarmos os dados da equação em uma dose fixa, podemos tirar as seguintes conclusões, que confirmam as dependências experimentais dadas acima da resistência ao estresse mecânico:

1.
A resistência de amostras não irradiadas de silício eletrônico aumenta sob compressão (Fig. 2). Isso ocorre devido ao crescimento significativo do fator β ₂ sob a ação de esforços mecânicos. Durante a compressão, a mudança (crescimento) do fator β ₂ excede significativamente a mudança (aumento) na mobilidade dos orifícios sob o aumento do estresse mecânico. Quanto ao parâmetro β ₁ , seu valor não depende de σ _meh .

Assim, no nosso caso, o aumento da resistência (compressão) e diminuição (descompressão) da carga para os cristais não irradiados à base de silício eletrônico pode ser explicado pelo movimento dos deslocamentos, que estão assumindo os principais portadores. Forças que causam movimento de defeitos, a coagulação de cachos e a condensação de cachos em deslocamentos [15] aparecem na rede cristalina elasticamente deformada. Os defeitos estão se tornando centros de captura de portadores principais enquanto coagulam em aglomerados maiores como microporos, aglomerados de silício internodo e impurezas. O acúmulo de defeitos na camada superficial de silício tende a reduzir sua condutividade. É exibido pelo fator de crescimento correspondente β ₂ na fórmula para a condutividade da superfície.
2.
A resistência das amostras irradiadas de silício eletrônico muda ligeiramente sob compressão (Fig. 3a). Isso é causado pela redução da mudança (crescimento) do fator β ₂ , devido ao movimento de deslocamento impedido. Em outras palavras, mudanças de parâmetros que competem entre si β ₂ e μ _p são proporcionais à compressão de amostras irradiadas de silício eletrônico.

A redução da resistência dos cristais eletrônicos de silício em combinação com o aumento da tensão (Fig. 3b) ocorre devido à diminuição da massa longitudinal efetiva de orifícios pesados [16, 17] e um aumento correspondente em sua mobilidade sob compressão. Isso é exibido pelo aumento de mobilidade correspondente μ _p na fórmula para a condutividade da superfície.
3.
A resistência de amostras irradiadas e não irradiadas de silício solar diminui ligeiramente sob compressão (Fig. 4). O processo de movimento de deslocamento é muito difícil para essas amostras experimentais. Além disso, defeitos adicionais que se movem do meio para a superfície do silício fazem a contribuição não essencial para o transporte de corrente no fundo de alta concentração de defeitos superficiais existentes nos cristais de silício solar. A ação da radiação aumenta adicionalmente a concentração de defeitos superficiais nos cristais de silício solar. Assim, mudanças de parâmetros que competem entre si β ₂ e μ _p são proporcionais à compressão de amostras irradiadas e não irradiadas de silício solar.

O efeito da radiação (Fig. 4b) aumenta adicionalmente a concentração de defeitos superficiais nos cristais de silício solar. Portanto, defeitos adicionais, que se movem devido ao gettering, contribuem pouco para o transporte de corrente do que para os cristais não irradiados.

Conclusões

Dois fatores principais que afetam a resistência do cristal de p-Si devem ser considerados durante a carga mecânica. O primeiro fator é um aumento da resistência com o aumento da carga (compressão) e uma diminuição da resistência com a diminuição da carga (desprendimento) devido ao processo de movimento de deslocamentos, que está assumindo os principais portadores. O segundo fator é a diminuição da resistência dos cristais de silício com o aumento da carga devido à diminuição da massa efetiva dos orifícios e um aumento correspondente em sua mobilidade.

A irradiação de raios X provoca a geração de vagas e átomos intersticiais no silício, que atuam como rolhas para o movimento dos deslocamentos. Devido ao aumento na difusão dos defeitos de radiação, a mobilidade dos orifícios diminui ligeiramente durante a irradiação de raios-X. Nos cristais de silício solar não irradiados, os defeitos existentes desempenham o papel de rolhas para o movimento dos deslocamentos.

Cristais de p-Si experimentais pré-irradiados (silício eletrônico e "baseado em energia solar") têm a propriedade de alterar ligeiramente sua resistividade (± 0,2%) sob a influência da compressão uniaxial (velocidade de fornecimento de tensão de 8 μ / min), dentro do deformação elástica ao longo do fluxo [\ (11 \ overline {2} \)].

Nas amostras eletrônicas de p-Si pré-irradiadas, a dependência da resistência ao estresse mecânico uniaxial depende significativamente da taxa de compressão. Em uma baixa velocidade de fornecimento de tensão (8 μm / min), a resistência aumenta com o aumento da tensão mecânica; em altas velocidades (32 μm / min), diminui. Para cristais baseados em silício solar tipo p, a dependência da resistência sob carga mecânica é independente da taxa de compressão.

Abreviações

ρ ( σ ):: A mudança de condutividade mecânica induzida ao longo da direção de deformação

Nanotubos de titanato Nanocompósitos de óxido de grafeno decorado:Preparação, Retardância de Chama e Fotodegradação Membranas compostas contendo nanopartículas de trocadores de íons inorgânicos para dessalinização eletrodialítica de glicerol

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias