Bistabilidade ótica controlável e mistura de quatro ondas em uma molécula fotônica optomecânica

Resumo

Teoricamente, investigamos os fenômenos ópticos não lineares, incluindo o processo de biestabilidade óptica e mistura de quatro ondas (FWM) em um sistema optomecânico de cavidade de molécula fotônica composta. A cavidade da molécula fotônica consistia em duas microcavidades de modo de galeria sussurrante (WGM), onde uma cavidade WGM é uma cavidade optomecânica com alta dissipação de cavidade κ e a outra cavidade WGM é uma cavidade ótica comum auxiliar com fator de alta qualidade (Q). Controlar os parâmetros do sistema, como a força de acoplamento J entre as duas cavidades, a razão da taxa de decaimento δ das duas cavidades, e a potência da bomba P , a biestabilidade óptica pode ser controlada. Além disso, o processo FWM que apresenta a divisão de modo normal também é investigado no espectro FWM sob diferentes regimes de parâmetros. Nosso estudo pode fornecer uma visão mais aprofundada dos fenômenos não lineares nos sistemas optomecânicos de moléculas fotônicas compostas.

Histórico

Os sistemas optomecânicos (OMS) [1], consistindo em cavidades ópticas acopladas a ressonadores mecânicos e explorando interações fóton-fônon coerentes induzidas por pressão de radiação, têm recentemente atraído muita atenção porque oferecem uma plataforma para manipular ressonadores mecânicos e campos eletromagnéticos, e pavimentar o forma de aplicações potenciais de dispositivos optomecânicos, como o laser de fônon [2, 3], detecção [4], compressão de fônon [5], a realização de luz comprimida [6-8], resfriamento do estado fundamental [9-11], e transparência induzida optomecanicamente (OMIT) [12-15] -induzida pela luz armazenada em dispositivos de estado sólido [16, 17]. Embora muita atenção tenha sido dada ao único OMS, para realizar OMS composto integrando mais modos ópticos ou mecânicos, como um modo mecânico acoplado a dois modos ópticos por meio de pressão de radiação [18, 19] e a interação fonônica entre dois ressonadores mecânicos [20 , 21] tornam-se uma tendência para uma investigação mais aprofundada do OMS e suas aplicações potenciais no processamento de informações quânticas. Com base no composto híbrido OMS, a transferência de um estado quântico [22], resfriamento de fônon semelhante a OMIT [23], modo escuro optomecânico [24] e absorção eletromagnética induzida por fônon [25] foi amplamente pesquisada. No numeroso composto OMS, como uma extensão natural do OMS genérico, duas microcavidades de modo de galeria sussurrante diretamente acopladas (WGM) denominadas molécula fotônica [26, 27] com efeito optomecânico em uma microcavidade WGM têm atraído muita atenção. Existem dois tipos de interação no sistema optomecânico da molécula fotônica composta:o primeiro é a interação optomecânica induzida pela pressão de radiação e o outro é o acoplamento cavidade-cavidade via tunelamento de fótons sintonizável. As duas interações juntas dão origem a vários fenômenos interessantes, incluindo o lasing de fônon [2, 3], o caos [28], o resfriamento do estado fundamental [23] e o controle coerente da transmissão de luz [25, 29, 30].

Por outro lado, o OMS também fornece uma plataforma para investigar o efeito não linear da interação luz-matéria. Entre todos os fenômenos não lineares em OMS, biestabilidade óptica e mistura de quatro ondas (FWM) são fenômenos ópticos não lineares típicos com foco no interesse dos pesquisadores. Recentemente, o comportamento biestável do número médio de fótons intracavitários foi extensivamente estudado em vários OMS, como o sistema optomecânico de cavidade condensada de Bose-Einstein [31, 32], OMS com um poço quântico [33], átomos ultracold [34, 35], e outro híbrido OMS [36, 37]. Além disso, FWM pode ser descrito como a cavidade acionada por uma forte bomba de laser com frequência ω _p e uma frequência de laser de sonda fraca ω _s , e então, dois fótons da bomba se misturariam com um fóton sonda através do modo mecânico para produzir um fóton livre na frequência 2 ω _p - ω _s em OMS, e também é investigado em trabalhos anteriores, como a divisão de modo em sistema optomecânico de forte acoplamento [38], OMS de acionamento mecânico coerente [39, 40] e um sistema optomecânico de cavidade bimodal [41]. No entanto, biestabilidade óptica e FWM têm sido raramente estudados em OMS de molécula fotônica composta, onde a força de acoplamento representada por J das duas cavidades desempenham um papel fundamental afetando esses fenômenos ópticos não lineares.

No presente trabalho, consideramos um sistema optomecânico de cavidade de molécula fotônica composta, consistindo de duas microcavidades WGM, onde uma cavidade WGM é uma cavidade optomecânica com alta dissipação de cavidade κ , e a outra cavidade WGM é uma cavidade ótica ordinária auxiliar com fator de alta qualidade (Q) [42]. Como Liu et al. [43] demonstraram, ainda é difícil alcançar fator Q alto e volume de modo pequeno (V) simultaneamente para o mesmo tipo de ressonador. Na optomecânica da molécula fotônica, por meio do acoplamento da cavidade originalmente optomecânica c com dissipação de alta cavidade κ (sem Q alto) para um modo de cavidade auxiliar a com Q alto, mas V grande, o requisito de Q alto e V pequeno para a mesma cavidade pode ser removido. Introduzimos um parâmetro de razão δ = κ _c / κ _a , onde κ _c = ω _c / Q _c e κ _a = ω _a / Q _a são as taxas de decaimento dos modos de cavidade c e a ( ω _c e ω _a são as frequências de cavidade c e a ) para investigar o efeito não linear na optomecânica da molécula fotônica. Aqui, a cavidade optomecânica c é acionado pela bomba de laser enquanto a cavidade auxiliar a é conduzido pelo laser da sonda. A cavidade c está acoplado à cavidade a via campo evanescente, e a força de acoplamento J entre as duas cavidades pode ser controlado variando a separação entre as duas cavidades WGM [26]. Investigamos a biestabilidade óptica e FWM com base na molécula fotônica composta OMS, variando a força de acoplamento J entre os ressonadores de cavidade, e uma biestabilidade óptica ajustável e controlável e FWM podem ser alcançados com a manipulação da força de acoplamento J entre as duas cavidades. Além disso, com o ajuste do parâmetro δ e a potência da bomba P , o processo FWM pode ser controlado.

Modelo e teoria

A optomecânica da molécula fotônica é mostrada na Fig. 1. A primeira cavidade suporta um modo óptico c com a frequência ω _c acionado pela bomba de laser com frequência ω _p e a amplitude \ (\ varepsilon _ {p} =\ sqrt {P / \ hbar \ omega _ {p}} \). A pressão de radiação induz um modo mecânico b com a frequência do ressonador mecânico ω _m , e a taxa de acoplamento optomecânico de fóton único é g = g ₀ x ₀ ( g ₀ = ω _c / R e R é o raio da cavidade c ), e a flutuação do ponto zero da posição do oscilador mecânico é \ (x_ {0} =\ sqrt {\ hbar / 2M \ omega _ {m}} \) [13]. Então, o hamiltoniano da optomecânica c é [13]

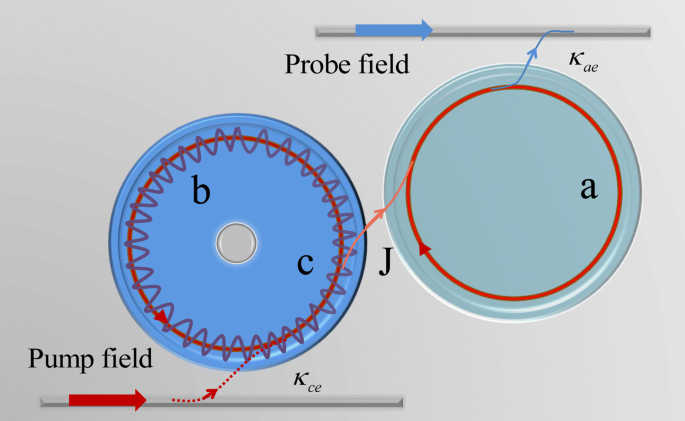
Diagrama esquemático do sistema optomecânico da cavidade da molécula fotônica composta, incluindo duas cavidades WGM. A primeira cavidade WGM com dissipação de alta cavidade κ é a cavidade optomecânica c conduzido por uma bomba de laser, e a força de pressão de radiação induz o modo mecânico b acoplamento à cavidade c com força de acoplamento g . A segunda cavidade WGM a é uma cavidade auxiliar acionada por uma sonda a laser com fator de alta qualidade (Q). A cavidade optomecânica c está acoplado à cavidade a via campo evanescente, e introduzimos um parâmetro J descrever a resistência de acoplamento das duas cavidades, que pode ser controlada variando a separação entre elas [26]
$$ H_ {c} =\ hbar \ Delta_ {c} c ^ {\ dag} c + \ hbar \ omega_ {m} b ^ {\ dag} b- \ hbar ga ^ {\ dag} a \ left (b ^ {\ dag} + b \ right) + i \ hbar \ sqrt {\ kappa_ {ce}} \ varepsilon_ {p} \ left (c ^ {\ dag} -c \ right), $$ (1)
onde Δ _c = ω _c - ω _p é a desafinação do campo da bomba e da cavidade c . c e c ^† representam os operadores de aniquilação e criação bosônica do modo de cavidade c , e b ^† ( b ) é o operador de criação (aniquilação) do modo mecânico. A cavidade auxiliar suporta apenas um modo óptico a conduzido pelo laser da sonda com frequência ω _s , e sua amplitude ε _s é \ (\ varepsilon _ {s} =\ sqrt {P_ {s} / \ hbar \ omega _ {s}} \). Apresentamos os operadores de aniquilação e criação a e a ^† para descrever a cavidade a , e seu hamiltoniano é [13]
$$ H_ {a} =\ hbar \ Delta_ {a} a ^ {\ dag} a + i \ hbar \ sqrt {\ kappa_ {ae}} \ varejpsilon_ {s} \ left (a ^ {\ dag} e ^ {-i \ Omega t} -ae ^ {i \ Omega t} \ right) $$ (2)
onde Δ _a = ω _a - ω _p é a desafinação do campo da bomba e da cavidade a e Ω = ω _s - ω _p é a desafinação da sonda da bomba. Usamos duas fibras cônicas para excitar o modo de cavidade a e modo de cavidade c como o guia de onda óptico com a taxa de acoplamento κ _ae e κ _ce . A cavidade optomecânica c casais com cárie a através de um campo evanescente, e a taxa de acoplamento cavidade-cavidade J pode ser ajustado de forma eficiente mudando a distância entre eles [26]. Quando a força de acoplamento J é fraca entre as duas cavidades, então a energia da cavidade c não pode ser transferido facilmente para a cavidade a . Por outro lado, se a força de acoplamento J aumenta com a diminuição da distância entre as duas cavidades, então a energia pode fluir facilmente das duas cavidades. A interação linearmente acoplada entre as duas cavidades é descrita por [26] \ (\ hbar J \ left (a ^ {\ dag} c + ac ^ {\ dag} \ right) \). Então, o hamiltoniano total no quadro de onda rotativa da frequência da bomba ω _c pode ser escrito [3, 13, 23]
$$ \ begin {alinhados} H =&\ hbar \ Delta_ {a} a ^ {\ dag} a + \ hbar \ Delta_ {c} c ^ {\ dag} c + \ hbar \ omega_ {m} b ^ {\ dag } b + \ hbar J \ left (a ^ {\ dag} c + ac ^ {\ dag} \ right) - \ hbar ga ^ {\ dag} a \ left (b ^ {\ dag} + b \ right) \ \ &+ i \ hbar \ sqrt {\ kappa_ {ce}} \ varepsilon_ {p} \ left (c ^ {\ dag} -c \ right) + i \ hbar \ sqrt {\ kappa_ {ae}} \ varepsilon_ { s} \ left (a ^ {\ dag} e ^ {- i \ Omega t} -ae ^ {i \ Omega t} \ right). \ end {alinhado} $$ (3)
A taxa de decaimento do modo de duas cavidades κ = κ _c = κ _a = κ _ex + κ ₀ com a taxa de perda intrínseca de fótons κ ₀ e κ _ex descreve a taxa na qual a energia deixa a cavidade óptica em campos de propagação [13]. Aqui, para simplificar, consideramos apenas a condição de κ _ex = κ ₀ = κ _ae = κ _ce , e consideramos ω _c = ω _a .

Usamos a equação de movimento de Heisenberg \ (i \ hbar \ partial _ {t} O =[O, H] \) ( O = a , c , X ) e introduzir os operadores de amortecimento e ruído correspondentes, e obtemos as equações quânticas de Langevin como segue [44]:
$$ \ partial_ {t} a =- (i \ Delta_ {a} + \ kappa_ {a}) a-iJc + \ sqrt {\ kappa_ {ae}} \ varejpsilon_ {s} e ^ {- i \ Omega t} + \ sqrt {2 \ kappa_ {a}} a _ {\ text {in}}, $$ (4) $$ \ partial_ {t} c =- (i \ Delta_ {c} + \ kappa_ {c}) c + igcX-iJa + \ sqrt {\ kappa_ {ce}} \ varepsilon_ {p} + \ sqrt {2 \ kappa_ {c}} c _ {\ text {in}}, $$ (5) $$ \ partial_ {t} ^ {2} X + \ gamma_ {m} \ partial_ {t} X + \ omega_ {m} ^ {2} X =2g \ omega_ {m} c ^ {\ dagger} c + \ xi, $$ (6)
onde X = b ^† + b é o operador de posição e γ _m é a taxa de decaimento do ressonador. a _em e c _em descrever os ruídos de Langevin segue as relações [45]
$$ \ begin {array} {@ {} rcl @ {}} \ left \ langle a _ {\ text {in}} (t) a _ {\ text {in}} ^ {\ dagger} \ left (t ^ { ^ {\ prime}} \ right) \ right \ rangle &=&\ left \ langle c _ {\ text {in}} (t) c _ {\ text {in}} ^ {\ dagger} \ left (t ^ { ^ {\ prime}} \ right) \ right \ rangle =\ delta \ left (tt ^ {^ {\ prime}} \ right), \ end {array} $$ (7) $$ \ begin {array} { @ {} rcl @ {}} \ left \ langle a _ {\ text {in}} (t) \ right \ rangle &=&\ left \ langle c _ {\ text {in}} (t) \ right \ rangle =0 \ end {array} $$ (8)
O modo ressonador é influenciado pelo processo de força estocástica com a seguinte função de correlação [46]
$$ \ left \ langle \ xi ^ {\ dagger} (t) \ xi \ left (t ^ {^ {\ prime}} \ right) \ right \ rangle \, =\, \ frac {\ gamma_ {m} } {\ omega_ {m}} \ int \! \ frac {d \ omega} {2 \ pi} \ omega e ^ {- i \ omega \ left (tt ^ {^ {\ prime}} \ right)} \ left [1 \, + \, \ coth \ left (\ frac {\ hbar \ omega} {2 \ kappa_ {B} T} \ direita) \ direita], $$ (9)
onde k _B é constante de Boltzmann e T indica a temperatura do reservatório.

Quando a cavidade optomecânica c é acionado por uma forte bomba de laser, o operador de Heisenberg pode ser dividido em duas partes, ou seja, valor médio de estado estacionário O ₀ , e pequena flutuação δ O com valor médio zero 〈 δ O 〉 =0. Os valores de estado estacionário determinam os números de fótons intracavitários ( n _a =| a _s | ² e n _c =| c _s | ² ) determinado por
$$ n_ {c} =\ frac {\ kappa_ {ce} \ varepsilon_ {p} ^ {2} \ left (\ Delta_ {a} ^ {2} + \ kappa_ {a} ^ {2} \ right)} {\ left (\ Delta ^ {^ {\ prime} 2} + \ kappa_ {c} ^ {2} \ right) \ left (\ Delta_ {a} ^ {2} + \ kappa_ {a} ^ {2} \ right) + 2J ^ {2} \ left (\ kappa_ {a} \ kappa_ {c} - \ Delta ^ {^ {\ prime}} \ Delta_ {a} \ right) + J ^ {4}}, $ $ (10) $$ n_ {a} =\ frac {\ kappa_ {ce} \ varepsilon_ {p} ^ {2} J ^ {2}} {\ left (\ Delta ^ {^ {\ prime} 2} + \ kappa_ {c} ^ {2} \ right) \ left (\ Delta_ {a} ^ {2} + \ kappa_ {a} ^ {2} \ right) + 2J ^ {2} \ left (\ kappa_ {a } \ kappa_ {c} - \ Delta ^ {^ {\ prime}} \ Delta_ {a} \ right) + J ^ {4}}, $$ (11)
onde \ (\ Delta ^ {^ {\ prime}} =\ Delta _ {c} -2g ^ {2} n_ {c} / \ omega _ {m} \). Esta forma de equações acopladas é característica da biestabilidade óptica. Na seção seguinte, discutiremos os parâmetros como a potência da bomba P , a resistência de acoplamento cavidade-cavidade J , e o parâmetro de razão δ que afetam a biestabilidade ótica. Mantendo apenas os termos lineares dos operadores de flutuação e fazendo o ansatz [47] 〈 δ a 〉 = a ₊ e ^{- i Ω t} + a _- e ^{i Ω t} , 〈 δ c 〉 = c ₊ e ^{- i Ω t} + c _- e ^{i Ω t} , 〈 δ X 〉 = X ₊ e ^{- i Ω t} + X _- e ^{i Ω t} , então obtemos
$$ a _ {-} =\ frac {\ Lambda_ {1}} {\ Lambda_ {2} - \ Lambda_ {3}}, $$ (12)
onde \ (\ Lambda _ {1} =igc_ {s} ^ {2} \ eta ^ {\ ast} J ^ {2} \ varepsilon _ {s} \ sqrt {\ kappa _ {ae}} \), Λ ₂ =( i Δ _{a 2} + κ _a ) ( i Δ ₂ + κ _c ) [( i Δ ₁ - κ _c ) ( i Δ _{a 1} - κ _a ) - J ² ], \ (\ Lambda _ {3} =- g ^ {2} \ eta ^ {\ ast 2} n_ {c} ^ {2} (i \ Delta _ {a1} - \ kappa _ {a}) ( i \ Delta _ {a2} + \ kappa _ {a}) \), Δ _{a 1} = Δ _a - Ω , Δ _{a 2} = Δ _a + Ω , \ (\ Delta _ {1} =\ Delta ^ {^ {\ prime}} - \ Omega + g \ eta n_ {c} \), \ (\ Delta _ {2} =\ Delta ^ {^ {\ prime}} + \ Omega + g \ eta ^ {\ ast} n_ {c} \), e \ (\ eta =2g \ omega _ {m} / (\ omega _ {m} ^ {2} -i \ gamma _ {m} \ Omega - \ Omega ^ {2}) \). Usando a relação padrão de entrada-saída [45] \ (a _ {\ text {out}} (t) =a _ {\ text {in}} (t) - \ sqrt {2 \ kappa _ {a}} a (t ) \), onde a _fora ( t ) é o operador de campo de saída e obtém o valor esperado dos campos de saída:
$$ {\ begin {alinhados} a _ {\ text {out}} (t) &=(\ varepsilon_ {p} - \ sqrt {\ kappa_ {ae}} a_ {s}) e ^ {- i \ omega_ { p} t} + (\ varepsilon_ {s} - \ sqrt {\ kappa_ {ae}} a _ {+}) e ^ {- i (\ delta + \ omega_ {p}) t} - \ sqrt {\ kappa_ { ae}} a _ {-} e ^ {- i (\ delta - \ omega_ {p}) t} \\ &=(\ varepsilon_ {p} - \ sqrt {\ kappa_ {ae}} a_ {s}) e ^ {- i \ omega_ {p} t} + (\ varepsilon_ {s} - \ sqrt {\ kappa_ {ae}} a _ {+}) e ^ {- i \ omega_ {s} t} - \ sqrt {\ kappa_ {ae}} a _ {-} e ^ {- i (2 \ omega_ {p} - \ omega_ {s}) t} \ end {alinhado}} $$ (13)
onde a _fora ( t ) é o operador de campo de saída. A equação (13) mostra que o campo de saída consiste em três termos. O primeiro termo corresponde ao campo de saída no campo de direção com amplitude ε _p e frequência ω _p . O segundo termo corresponde ao campo de prova com frequência ω _s relacionado ao campo anti-Stokes resultando em OMIT, que foi investigado em vários sistemas optomecânicos [12-15, 48]. O último corresponde ao campo de saída com frequência 2 ω _p - ω _s relacionado ao campo stoke exibindo o FWM. No processo FWM, os dois fótons do campo de direção interagem com um único fóton do campo de prova, cada um com frequências ω _p e ω _s nasceu um novo fóton de frequência 2 ω _p - ω _s . A intensidade FWM em termos do campo de prova pode ser definida como [49]
$$ \ text {FWM} =\ left \ vert \ frac {\ sqrt {\ kappa_ {ae}} a _ {-}} {\ varejpsilon_ {s}} \ right \ vert ^ {2} \ text {,} $ $ (14)
que é determinado pela força de acoplamento optomecânico g , a potência da bomba P , a resistência de acoplamento cavidade-cavidade J , e a razão da taxa de decaimento δ das duas cavidades.

Resultados numéricos e discussões

Nesta seção, primeiro investigamos o comportamento biestável do número de fótons em estado estacionário n _c e n _a das duas cavidades de acordo com as Eqs. (10) e (11). Por ser muito complicado fornecer a expressão analítica da condição de biestabilidade, apresentaremos aqui os resultados numéricos. Escolhemos os parâmetros semelhantes aos da Ref. [13, 26]:os parâmetros da cavidade c como [13]: g ₀ =12 GHz / nm, γ _m =41 kHz, ω _m =51,8 MHz, κ _c =5 MHz, m =20 ng, λ =750 nm, e Q =1500, e a ordem de magnitude da potência da bomba é miliwatt (1 mW =10 ⁻³ C). Para cavidade a , consideramos ω _a = ω _c e κ _c = κ _a . A força de acoplamento J entre os dois modos de cavidade desempenha um papel fundamental e pode afetar o comportamento biestável e FWM. Foi relatado experimentalmente que a força de acoplamento J depende da distância entre a cavidade c e cavidade a [26] (também a resistência de acoplamento diminui exponencialmente com o aumento da distância das duas cavidades). Aqui, esperamos a força de acoplamento \ (J \ sim \ sqrt {\ kappa _ {c} \ kappa _ {a}} \).

Equações (10) e (11) dando os números de fótons intracavidade da cavidade optomecânica c e cavidade comum a são equações cúbicas acopladas, que exibem comportamento biestável. Primeiro consideramos a condição de J =0, ou seja, apenas uma única cavidade optomecânica c , e a Fig. 2a representa o número médio de fótons intracavitários n _c da cavidade optomecânica c em função da desafinação da bomba de cavidade Δ _c = ω _c - ω _p com três potências de bomba. Quando a potência da bomba é inferior a P =0,4 mW (como P =0,1 mW), a curva é quase Lorentziana. Com o aumento do poder P a um valor crítico, a cavidade optomecânica c exibe comportamento biestável, conforme mostrado nas curvas para P =0,4 mW a P =0,8 mW, onde a curva de ressonância inicialmente Lorentziana torna-se assimétrica. O número médio de fótons intracavitários n _c tem três raízes reais (Eq. (10)), sendo que a maior e a menor são estáveis, e a do meio é instável, representada em forma oval na Fig. 2a. No entanto, quando consideramos a cavidade óptica a , ou seja, J ≠ 0 como J =1.0 κ _a , o comportamento biestável é quebrado de algumas maneiras, conforme mostrado na Fig. 2b. Isso porque quando cavidade optomecânica c acoplado à cavidade óptica a , partes do número do fóton intracavitário n _c da cavidade optomecânica c será acoplado à cavidade óptica a e, portanto, número de fótons intracavitários n _c diminuirá e resultará em um comportamento biestável destruído. A Figura 2c mostra o número médio de fótons intracavitários n _c da cavidade optomecânica c em função da resistência de acoplamento cavidade-cavidade J com três potências de bomba. Obviamente, o número médio de fótons intracavitários n _c depende da potência da bomba P , e o número do fóton intracavitário n _c está sempre diminuindo com o aumento da força de acoplamento J porque as partes do número de fótons são acopladas à cavidade óptica a . Além disso, uma maior desafinação da bomba de cavidade é benéfica para observar o comportamento biestável óptico com o aumento da potência da bomba P . A Figura 2d representa o número médio de fótons intracavitários n _c versus a potência da bomba P com cavidade a nas faixas laterais vermelhas ( Δ _a = ω _m ) e bandas laterais azuis ( Δ _a =- ω _m ), respectivamente, e a biestabilidade apresenta o comportamento da malha de histerese [50]. No entanto, nossos resultados são diferentes do trabalho anterior de sistema optomecânico bimodal sem considerar o acoplamento cavidade-cavidade J . Portanto, a força de acoplamento J desempenha um papel importante na biestabilidade.

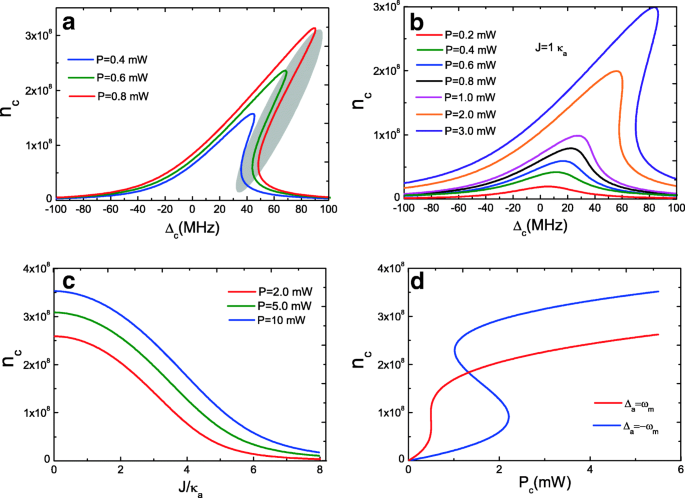
a Número médio de fótons intracavitários da cavidade optomecânica c em função da desafinação da bomba de cavidade Δ _c com três potências de bomba em J =0. b Número médio de fótons intracavitários da cavidade optomecânica c em função da desafinação da bomba de cavidade Δ _c com vários poderes de bomba diferentes em J =1.0 κ _a . c Número médio de fótons intracavitários n _c da cavidade optomecânica c como uma função de J com três potências de bomba. d Número médio de fótons intracavitários n _c como uma função de P para Δ _c = Δ _a = ω _m

Investigamos ainda mais o comportamento biestável da cavidade óptica a com Eq. (11). A Figura 3a fornece o número de fótons intracavitários n _a de cavidade comum a em função da desafinação da bomba de cavidade Δ _a = ω _a - ω _p com potência de bomba P =0,1 mW, P =1,0 mW e P =10 mW em J =1.0 κ _a . É óbvio que a cavidade óptica a não pode se comportar como um comportamento biestável devido ao número de fótons intracavitários n _a de cavidade a da cavidade c não pode manter a biestabilidade em baixa potência da bomba. Na verdade, apenas alta potência da bomba P lata cavidade a apresentam comportamento biestável, porque somente cavidade optomecânica acionada por alta potência de bomba c , muito mais número de fótons pode se acoplar na cavidade óptica a . Também representamos o número médio de fótons intracavitários n _a da cavidade óptica a em função da força de acoplamento J sob três potências de bomba, conforme mostrado na Fig. 3b. É claro que quando J =0, n _a =0, porque não há acoplamento entre as duas cavidades em J =0, e nesta condição, nenhum fóton se acopla à cavidade óptica a . Com o aumento da força de acoplamento J (diminuindo a distância das duas cavidades [26]), os números de fótons intracavitários n _a de cavidade óptica comum a aumentam, mas nem sempre. Existe uma força de acoplamento ideal J para o valor máximo de n _a sob potência de bomba diferente, e então, n _a diminuirá com o aumento de J . É um fato notável que a força de acoplamento J entre as duas cavidades pode ser ajustado [26].

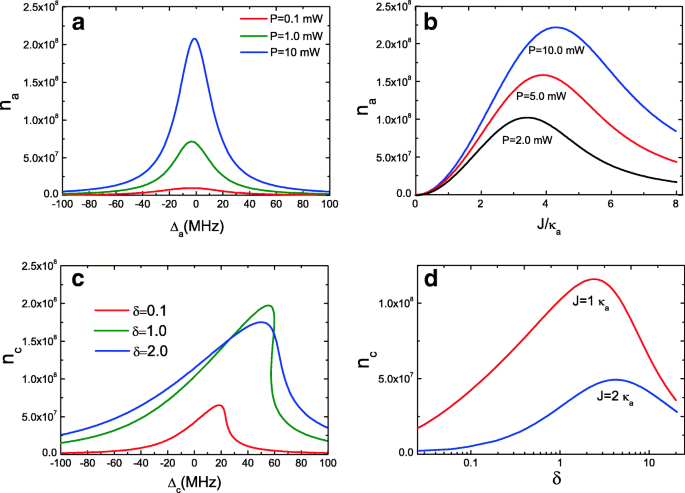
a Número médio de fótons intracavitários da cavidade comum a em função da desafinação da bomba de cavidade Δ _a com três potências de bomba em J =1.0 κ _a . b Número médio de fótons intracavitários n _a como uma função de J com três potências de bomba. c Número médio de fótons intracavitários n _c como uma função de Δ _c com três parâmetros de razão δ . d Número médio de fótons intracavitários n _c como uma função de δ para dois J

Além disso, consideramos um parâmetro de razão δ = κ _c / κ _a ( κ _c = ω _c / Q _c e κ _a = ω _a / Q _a ) para investigar os parâmetros das duas cavidades que influenciam o comportamento biestável. κ é a taxa de decaimento do modo de cavidade, que está relacionado à frequência e ao fator de qualidade da cavidade. Como sabemos, é difícil alcançar Q alto e V pequeno simultaneamente para um modo de cavidade devido ao limite de difração. Para uma cavidade óptica, um V menor correspondendo a uma taxa de decaimento radiativo maior resulta em um Q mais baixo. Embora diferentes tipos de cavidades possuam suas próprias propriedades únicas, o peso entre Q alto e V pequeno ainda existe. No entanto, ao acoplar o OMS original c com dissipação de alta cavidade para um modo de cavidade auxiliar a com Q alto, mas V grande, o comportamento biestável mudará significativamente. A Figura 3c mostra o número médio de fótons intracavitários n _c da cavidade optomecânica c como uma função de Δ _a sob vários δ diferentes = κ _c / κ _a com uma força de acoplamento inalterada J =1.0 κ _a . Podemos descobrir que o comportamento biestável pode aparecer, mas o número de fótons intracavidade n _c é pequeno em δ =0,1 com J =2 κ _a , ou seja, κ _c =0,1 κ _a o que significa Q _c> Q _a . Ao aumentar a proporção δ de δ =1,0 a δ =2.0, o número do fóton intracavitário n _c experimenta a mudança de comportamento biestável para perfil de linha quase Lorentziano. Isso quer dizer quando Q _c < Q _a , o comportamento biestável será interrompido, mas há uma condição ótima, ou seja, Q _c = Q _a . Na Fig. 3d, damos o número do fóton intracavitário n _c como uma função de δ com dois J diferentes , e obviamente, ao aumentar o parâmetro de razão δ , os números dos fótons intracavitários n _c aumentar. Quando atinge um valor ótimo para um determinado J , então n _c diminuir. Portanto, controlando os parâmetros da cavidade, como a taxa de decaimento κ ou o fator de qualidade das cavidades, o comportamento biestável pode ser controlado.

Por outro lado, como um fenômeno óptico não linear típico, também investigamos o processo FWM com a Eq. (14) no sistema optomecânico da molécula fotônica. A Figura 4 representa o espectro FWM em função da cavidade da sonda a desafinação Δ _s = ω _s - ω _a em Δ _a = Δ _c =0 sob diferentes regimes de parâmetros. A Figura 4a-d exibe a evolução dos espectros FWM sob diferentes potências de bomba P em J =1.0 κ _a . É claro que os espectros FWM apresentam três picos, onde um pico Lorentziano próximo a Δ _s =0 e dois picos de divisão de modo localizados em ± ω _m , e a intensidade do FWM diminui com o aumento da potência da bomba. A Figura 4e-h mostra a mudança dos espectros FWM de J =0,5 κ _a para J =2.0 κ _a na potência da bomba P =1,0 mW. Com o aumento da força de acoplamento J de J =0,5 κ _a para J =2.0 κ _a , os espectros FWM mudam significativamente. O fenômeno pode ser explicado com uma imagem do estado vestido que foi demonstrado em sistema optomecânico de cavidade única [51].

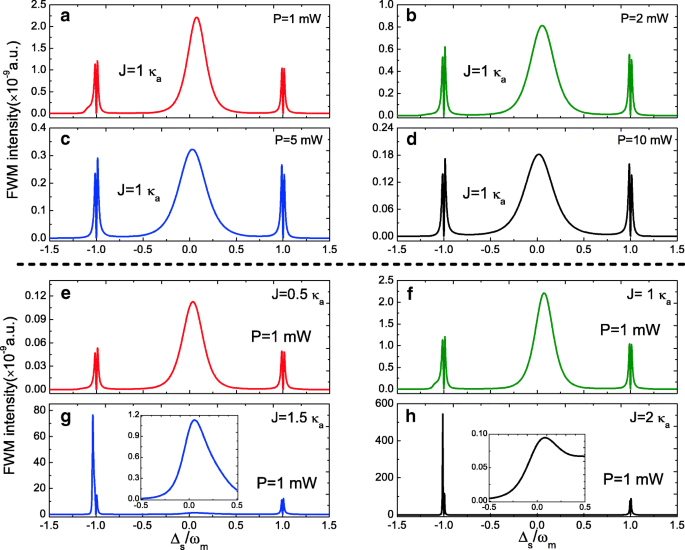
a - d Intensidade FWM em função da sintonia normalizada da bomba de sonda Δ _s para potência de bomba diferente em J =1.0 κ _a . e - h Intensidade FWM em função de Δ _s para diferentes J na potência da bomba P =1,0 mW

Em seguida, investigamos os espectros FWM em Δ _a = Δ _c ≠ 0. A Figura 5a-d fornece os espectros FWM na banda lateral vermelha, ou seja, Δ _a = Δ _c = ω _m sob um J inalterado =1.0 κ _a com o aumento da potência da bomba de P =1,0 a P =10 mW. Dois picos de divisão de modo normal aparecem no espectro FWM localizando em ± ω _m respectivamente, e a intensidade do FWM diminui com o aumento da potência da bomba. A Figura 5e-h mostra os espectros FWM na banda lateral vermelha, ou seja, Δ _a = Δ _c = ω _m sob uma potência de bomba fixa P =2,0 mW com aumento da força de acoplamento J de J =0,5 κ _a para J =2.0 κ _a . Obviamente, a intensidade do FWM aumenta com o aumento da força de acoplamento J , e o maior J significa mais números de fótons acoplados à cavidade óptica a . Ao alterar a dessintonização Δ _a e Δ _c da faixa lateral vermelha para a faixa lateral azul, ou seja, Δ _a = Δ _c =- ω _m , a evolução dos espectros FWM muda proeminentemente. A Figura 5i – l exibe os espectros FWM na banda lateral azul sob quatro diferentes potências da bomba, e a intensidade FWM diminui com o aumento da potência da bomba, mesmo na banda lateral azul. Exceto dois picos de divisão de modo normal localizados em ± ω _m , também há dois picos de banda lateral nítidos que aparecem nos espectros FWM e suas localizações estão relacionadas à potência da bomba. Na Fig. 5m-p, também discutimos a força de acoplamento J que afetam os espectros FWM sob a banda lateral azul. Se outros picos de banda lateral agudos aparecem nos espectros FWM depende da força de acoplamento J .

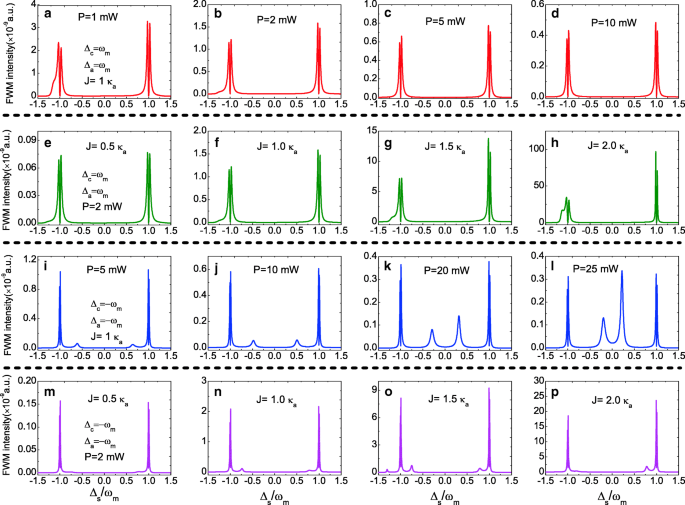
a - d Intensidade FWM em função de Δ _s para potência de bomba diferente P na faixa lateral vermelha ( Δ _c = Δ _a = ω _m ) e J =1.0 κ _a . e - h Intensidade FWM em função de Δ _s para diferentes J sob a faixa lateral vermelha e a potência da bomba P =2,0 mW. eu - l Intensidade FWM em função de Δ _s para potência de bomba diferente P na banda lateral azul ( Δ _c = Δ _a =- ω _m ) e J =1.0 κ _a . m - p Intensidade FWM em função de Δ _s para diferentes J sob a faixa lateral azul e a potência da bomba P =2,0 mW

Além disso, uma vez que o parâmetro de razão δ = κ _c / κ _a pode influenciar o número de fótons intracavitários na molécula fotônica composta OMS, os espectros FWM podem ser manipulados com o controle do parâmetro δ . A Figura 6a-h apresenta os espectros FWM em parâmetros inalterados J =2.0 κ _a e P =10 mW sob a banda lateral vermelha com o aumento da razão δ de δ =0,05 a δ =3,0, e a intensidade do FWM diminui com o aumento da proporção δ . Enquanto na banda lateral azul, outros picos de banda lateral agudos aparecerão nos espectros FWM como mostrado na Fig. 6i – p, e a intensidade FWM também diminui com o aumento da razão δ . Portanto, com o controle dos parâmetros da cavidade, como a taxa de decaimento κ ou o Q das cavidades, o FWM pode atingir diretamente no OMS de molécula fotônica composta.

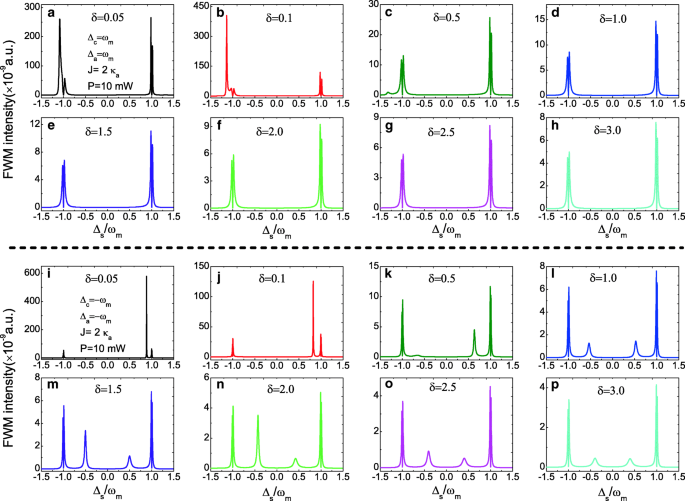
a - h Intensidade FWM em função de Δ _s para vários parâmetros de razão diferentes δ na faixa lateral vermelha ( Δ _c = Δ _a = ω _m ) e J =2.0 κ _a , P =10 mW. eu - p Intensidade FWM em função de Δ _s para vários parâmetros de razão diferentes δ na banda lateral azul ( Δ _c = Δ _a =- ω _m ) e J =2.0 κ _a , P =10 mW

Conclusão

We have investigated the optical bistability and four-wave mixing in a composite WGM cavity photonic-molecule optomechanical system, which includes an optomechanical cavity with high-cavity dissipation coupled to an auxiliary cavity with high-quality factor. We investigate the optical bistability under different parameter regimes such as the coupling strength J between the two cavities and the decay rate ratio δ of the two cavities in the system. The optical bistability can be adjusted by the pump field driving the optomechanical cavity, and the intracavity photon number in the two cavities is determined by the coupling strength J . Further, we have also demonstrated how to control the FWM process in the photonic-molecule optomechanical system under different driving conditions (the red sideband and the blue sideband) and different parameter conditions (the coupling strength J and the ratio δ ) Numerical results show that the FWM process can be controlled with such parameters. These results are beneficial for better understanding the nonlinear phenomena in the composite photonic-molecule optomechanical system.

Abreviações

C-OMS:: Cavity optomechanics systems
FWM:: Four-wave mixing
OMS:: Optomechanics systems
OMIT:: Optomechanically induced transparency
Q:: Quality
V:: Volume
WGM:: Whispering gallery mode

Acoplamento forte entre uma molécula quase única e uma cavidade plasmônica no sistema de captura Autopolarização de filme PVDF desencadeada por tratamento hidrofílico para sensor piroelétrico com ruído piezoelétrico ultrabaixo

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias