Resolvendo Equações Simultâneas:O Método de Substituição e o Método de Adição

O que são equações e sistemas de equações simultâneos?

Os termos equações simultâneas e sistemas de equações referem-se a condições em que duas ou mais variáveis ​​desconhecidas estão relacionadas entre si por meio de um número igual de equações.

Exemplo:

Para este conjunto de equações, há apenas uma única combinação de valores para x e y isso irá satisfazer a ambos.

Qualquer uma das equações, considerada separadamente, tem uma infinidade de (x, y) válidos soluções, mas juntos há apenas um. Traçada em um gráfico, essa condição se torna óbvia:







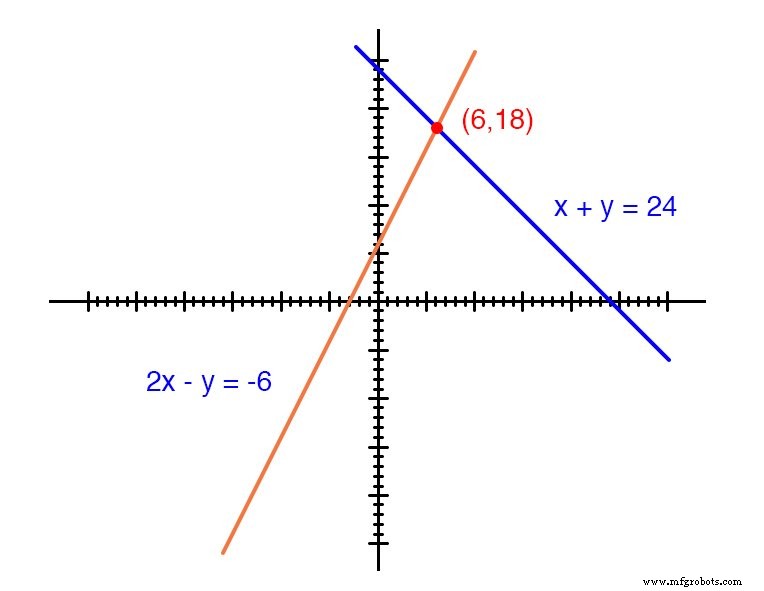
Cada linha é na verdade um continuum de pontos que representam possíveis x e y pares de solução para cada equação.

Cada equação, separadamente, tem um número infinito de pares ordenados ( x , y ) soluções. Existe apenas um ponto onde as duas funções lineares x + y =24 e 2x - y =-6 se cruzam (onde uma de suas muitas soluções independentes funciona para ambas as equações), e é aí que x é igual a um valor de 6 e y é igual a um valor de 18.

Normalmente, porém, a representação gráfica não é uma maneira muito eficiente de determinar o conjunto de soluções simultâneas para duas ou mais equações. É especialmente impraticável para sistemas de três ou mais variáveis.

Em um sistema de três variáveis, por exemplo, a solução seria encontrada pela interseção de pontos de três planos em um espaço de coordenadas tridimensional - o que não é um cenário fácil de visualizar.

Resolvendo equações simultâneas usando o método de substituição

Existem várias técnicas algébricas para resolver equações simultâneas.

Talvez o mais fácil de compreender seja a substituição método.

Tome, por exemplo, nosso exemplo de problema de duas variáveis:







No método de substituição, manipulamos uma das equações de forma que uma variável seja definida em termos da outra:







Então, pegamos esta nova definição de uma variável e substituir para a mesma variável na outra equação.

Neste caso, tomamos a definição de y , que é 24 - x e substitua este por y termo encontrado na outra equação:







Agora que temos uma equação com apenas uma única variável ( x ), podemos resolvê-lo usando técnicas algébricas "normais":







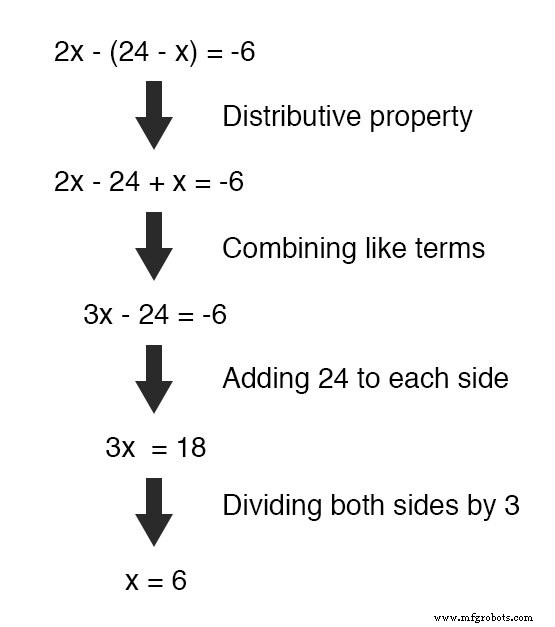
Agora que x é conhecido, podemos inserir esse valor em qualquer uma das equações originais e obter um valor para y.

Ou, para nos poupar trabalho, podemos inserir este valor (6) na equação que acabamos de gerar para definir y em termos de x , sendo que já está em um formulário para resolver para y :







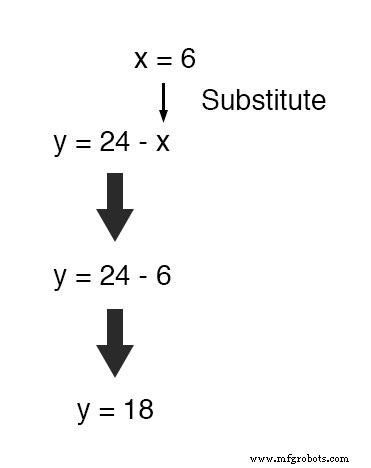
Aplicar o método de substituição a sistemas de três ou mais variáveis ​​envolve um padrão semelhante, apenas com mais trabalho envolvido.

Isso geralmente é verdadeiro para qualquer método de solução:o número de etapas necessárias para obter soluções aumenta rapidamente com cada variável adicional no sistema.

Para resolver três variáveis ​​desconhecidas, precisamos de pelo menos três equações. Considere este exemplo:







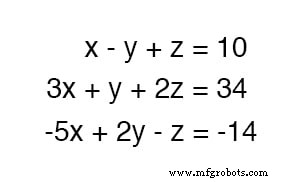
Sendo que a primeira equação possui os coeficientes mais simples (1, -1 e 1, para x , y e z , respectivamente), parece lógico usá-lo para desenvolver uma definição de uma variável em termos das outras duas.

Resolva para x em termos de y e z :







Agora, podemos substituir esta definição de x onde x aparece nas outras duas equações:







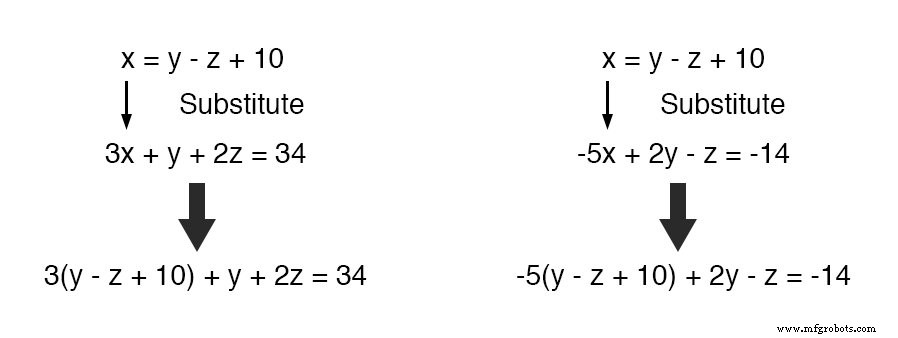
Reduzindo essas duas equações às suas formas mais simples:







Até agora, nossos esforços reduziram o sistema de três variáveis ​​em três equações para duas variáveis ​​em duas equações.

Agora, podemos aplicar a técnica de substituição novamente às duas equações 4y - z =4 e -3y + 4z =36 resolver para y ou z . Primeiro, vou manipular a primeira equação para definir z em termos de y :







A seguir, vamos substituir esta definição de z em termos de y onde vemos z na outra equação:







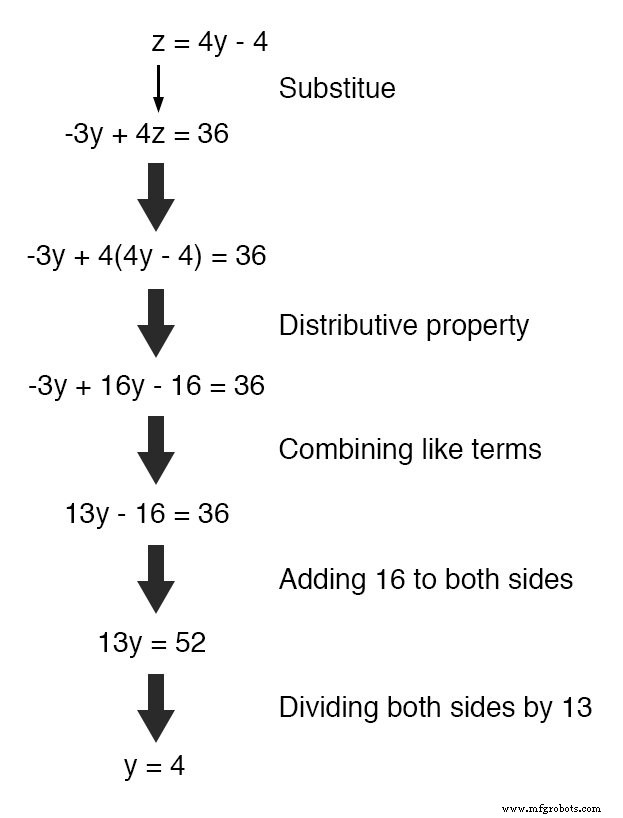
Agora que y é um valor conhecido, podemos inseri-lo na equação definindo z em termos de y e obter uma figura para z :







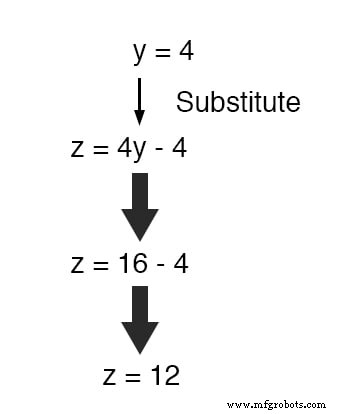
Agora, com valores para y e z conhecido, podemos conectá-los à equação onde definimos x em termos de y e z , para obter um valor para x :







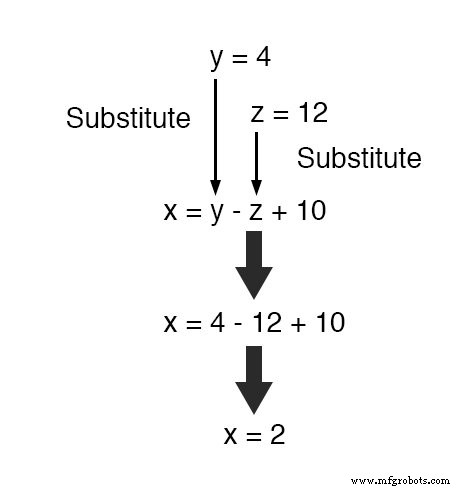
Para encerrar, encontramos valores para x , y e z de 2, 4 e 12, respectivamente, que satisfazem todas as três equações.

Resolvendo equações simultâneas usando o método de adição

Embora o método de substituição possa ser o mais fácil de entender em um nível conceitual, existem outros métodos de solução disponíveis para nós.

Um desses métodos é a chamada adição método, pelo qual as equações são adicionadas umas às outras com o propósito de cancelar os termos variáveis.

Vamos pegar nosso sistema de duas variáveis ​​usado para demonstrar o método de substituição:







Uma das regras de álgebra mais usadas é que você pode realizar qualquer operação aritmética que desejar em uma equação, desde que a faça igualmente para ambos os lados .

Com referência à adição, isso significa que podemos adicionar qualquer quantidade que desejarmos a ambos os lados de uma equação - desde que seja o mesmo quantidade - sem alterar a verdade da equação.

Uma opção que temos, então, é adicionar os lados correspondentes das equações para formar uma nova equação.

Uma vez que cada equação é uma expressão de igualdade (a mesma quantidade em ambos os lados do = sinal), adicionar o lado esquerdo de uma equação ao lado esquerdo da outra equação é válido, desde que adicionemos os lados direitos das duas equações também.

Em nosso conjunto de equações de exemplo, por exemplo, podemos adicionar x + y para 2x - y e adicione 24 e -6 juntos também para formar uma nova equação.

Que benefício isso traz para nós? Examine o que acontece quando fazemos isso com nosso conjunto de equações de exemplo:







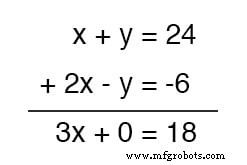
Porque a equação superior continha um y positivo termo enquanto a equação inferior continha um y negativo termo, esses dois termos cancelaram um ao outro no processo de adição, não deixando nenhum y prazo na soma.

O que nos resta é uma nova equação, mas com apenas uma única variável desconhecida, x ! Isso nos permite resolver facilmente o valor de x :







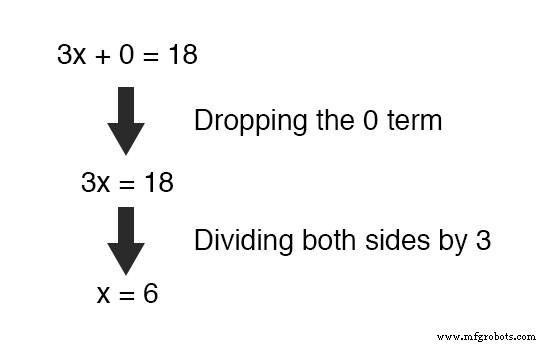
Assim que tivermos um valor conhecido para x , é claro, determinando y 'S valor é simplesmente uma questão de substituição (substituindo x com o número 6 ) em uma das equações originais.

Neste exemplo, a técnica de somar as equações funcionou bem para produzir uma equação com uma única variável desconhecida.

Que tal um exemplo em que as coisas não são tão simples? Considere o seguinte conjunto de equações:







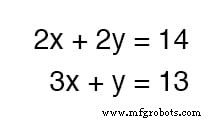
Poderíamos somar essas duas equações - sendo esta uma operação algébrica completamente válida - mas não nos beneficiaria no objetivo de obter valores para x e y :







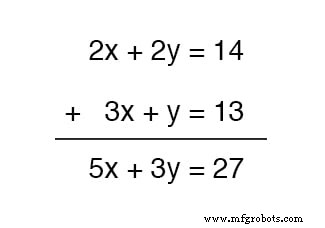
A equação resultante ainda contém duas variáveis ​​desconhecidas, assim como as equações originais, e por isso não estamos mais adiante na obtenção de uma solução.

No entanto, e se pudéssemos manipular uma das equações de modo a ter um termo negativo que seria cancelar o respectivo termo na outra equação quando adicionado?

Então, o sistema se reduziria a uma única equação com uma única variável desconhecida, assim como no último exemplo (fortuito).

Se pudéssemos virar o y termo na equação inferior em - 2y termo, de modo que quando as duas equações foram adicionadas, ambas y termos nas equações seriam cancelados, deixando-nos apenas com um x prazo, isso nos aproximaria de uma solução.

Felizmente, isso não é difícil de fazer. Se multiplicarmos cada termo da equação inferior por um -2 , ele produzirá o resultado que buscamos:







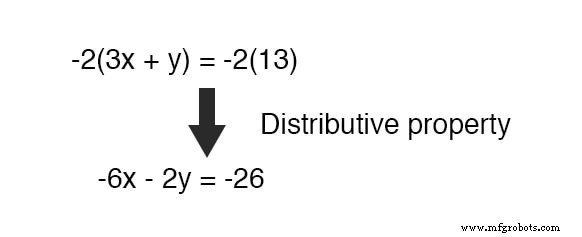
Agora, podemos adicionar esta nova equação à equação superior original:





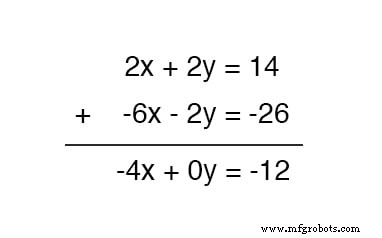
Resolvendo para x , obtemos um valor de 3 :







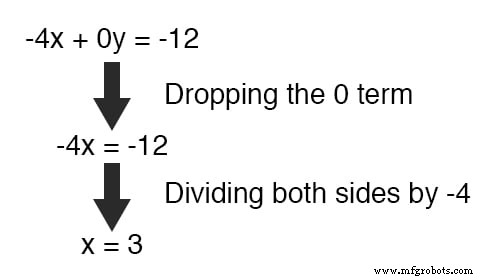
Substituindo este valor recém-encontrado por x em uma das equações originais, o valor de y é facilmente determinado:







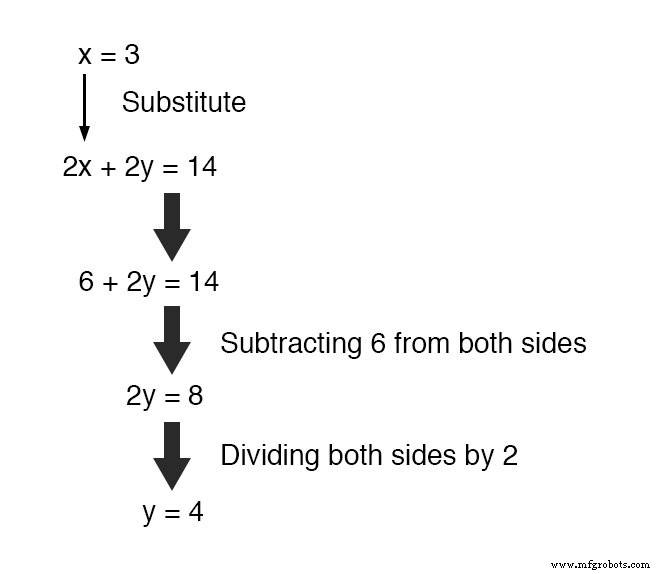
Usar essa técnica de solução em um sistema de três variáveis ​​é um pouco mais complexo.

Tal como acontece com a substituição, você deve usar esta técnica para reduzir o sistema de três equações de três variáveis ​​a duas equações com duas variáveis ​​e, em seguida, aplicá-la novamente para obter uma única equação com uma variável desconhecida.

Para demonstrar, vou usar o sistema de equação de três variáveis ​​da seção de substituição:







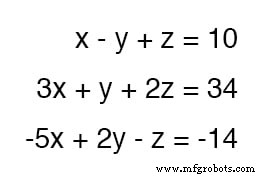
Sendo que a equação superior possui valores de coeficiente de 1 para cada variável, será uma equação fácil de manipular e usar como uma ferramenta de cancelamento.

Por exemplo, se desejarmos cancelar o 3x termo da equação do meio, tudo o que precisamos fazer é pegar a equação do topo e multiplicar cada um de seus termos por -3 , em seguida, adicione-o à equação do meio assim:







Podemos livrar a equação inferior de seu -5x termo da mesma maneira:pegue a equação original do topo, multiplique cada um de seus termos por 5 , em seguida, adicione essa equação modificada à equação inferior, deixando uma nova equação com apenas y e z termos:







Neste ponto, temos duas equações com as mesmas duas variáveis ​​desconhecidas, y e z :







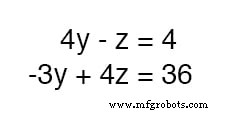
Por inspeção, deve ser evidente que o -z termo da equação superior pode ser aproveitado para cancelar o 4z termo na equação inferior se multiplicarmos cada termo da equação superior por 4 e some as duas equações:







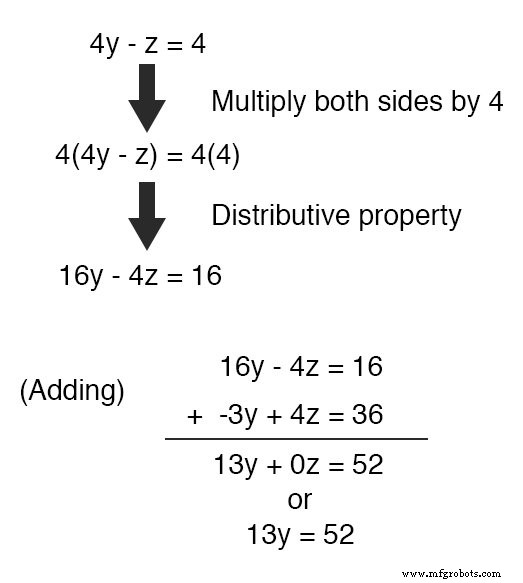
Pegando a nova equação 13y =52 e resolvendo para y (dividindo ambos os lados por 13 ), obtemos um valor de 4 para y .

Substituindo este valor de 4 para y em qualquer uma das equações de duas variáveis ​​nos permite resolver para z .

Substituindo ambos os valores de y e z em qualquer uma das equações originais de três variáveis ​​nos permite resolver para x .

O resultado final (vou poupar você das etapas algébricas, já que você já deve estar familiarizado com elas!) É que x =2 , y =4 e z =12 .



PLANILHAS RELACIONADAS:

• Equações simultâneas para planilha de análise de circuito

Fatoriais Trigonometria do Triângulo Direito