Relacionamentos booleanos nos diagramas de Venn

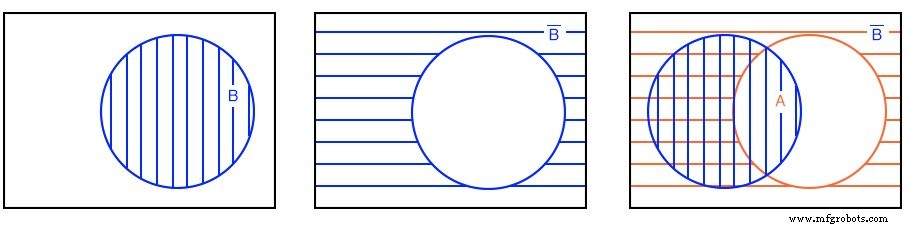
O quarto exemplo tem A parcialmente sobreposto B . Porém, primeiro olharemos para toda a área hachurada abaixo e, posteriormente, apenas a região sobreposta. Vamos atribuir algumas expressões booleanas às regiões acima, conforme mostrado abaixo.

Abaixo à esquerda, há uma área tracejada horizontal vermelha para A . Há uma área sombreada vertical azul para B .

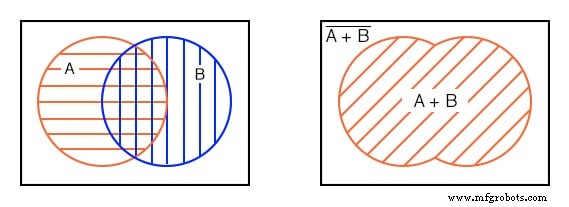
Se olharmos para toda a área de ambos, independentemente do estilo de hachura, a soma total de todas as áreas hachuradas, obtemos a ilustração acima certa, que corresponde ao OR inclusivo função de A, B. A expressão booleana é A + B .

Isso é mostrado pelo 45 ^o área hachurada. Qualquer coisa fora da área hachurada corresponde a (A + B) - não como mostrado acima. Vamos passar para a próxima parte do quarto exemplo.

A outra maneira de olhar para um diagrama de Venn com círculos sobrepostos é olhar apenas a parte comum a ambos A e B , a área hachurada dupla abaixo à esquerda. A expressão booleana para esta área comum correspondendo a AND função é AB conforme mostrado abaixo à direita. Observe que tudo fora de AB hachurado duplo é AB não .



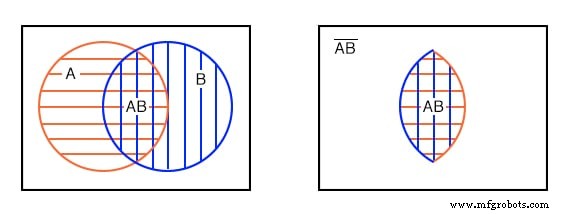
Observe que alguns dos membros de A , acima, são membros de (AB) ’ . Alguns dos membros de B são membros de (AB) ’ . Mas, nenhum dos membros de (AB) ’ estão dentro da área duplamente hachurada AB .



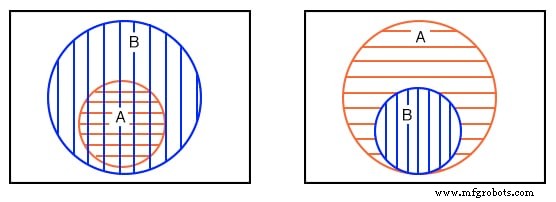
Repetimos o segundo exemplo acima à esquerda. Seu quinto exemplo, que você esboçou anteriormente, é fornecido acima, à direita, para comparação. Mais tarde, encontraremos o elemento ocasional, ou grupo de elementos, totalmente contido em outro grupo em um mapa de Karnaugh.

A seguir, mostramos o desenvolvimento de uma expressão booleana envolvendo uma variável complementada a seguir.



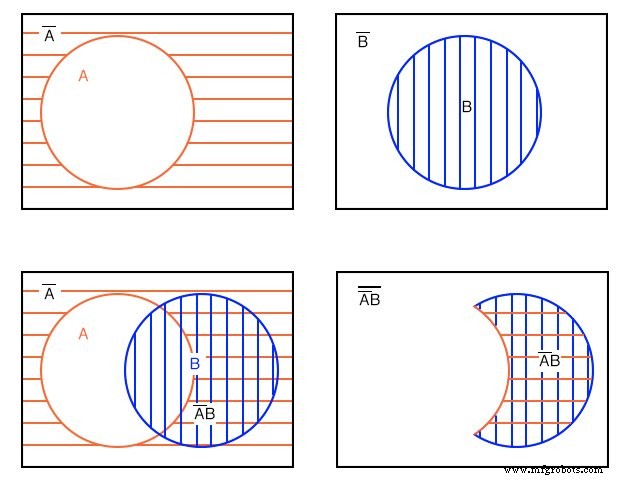
Exemplo: (acima)

Mostrar um diagrama de Venn para A’B (A-não E B).

Solução: Começando acima do canto superior esquerdo, temos o sombreado horizontal vermelho A ’ (A-não), então, canto superior direito, B . Em seguida, no canto inferior esquerdo, formamos a função AND A’B sobrepondo as duas regiões anteriores. A maioria das pessoas usaria isso como resposta ao exemplo apresentado.

No entanto, apenas o duplo hachurado A’B é mostrado à direita para maior clareza. A expressão A’B é a região onde A ’ e B sobreposição. A região limpa fora de A’B é (A’B) ’ , que não fazia parte do exemplo apresentado.

Vamos tentar algo semelhante com o booleano OR função.

Exemplo: Encontre B ’+ A



Solução: Acima à direita, começamos com B que é complementado com B ’ . Finalmente, sobrepomos A em cima de B ’ . Uma vez que estamos interessados ​​em formar o OU , estaremos procurando por todas as áreas hachuradas, independentemente do estilo de hachura. Assim, A + B ’ é toda a área hachurada acima à direita. É mostrado como uma única região hachurada abaixo à esquerda para maior clareza.



Exemplo: Encontre (A + B ’)’

Solução:

O verde 45 ^o A + B ’ a área hachurada foi o resultado do exemplo anterior. Seguindo para a para, (A + B ’)’ , o presente exemplo, acima à esquerda, vamos encontrar o complemento de A + B ’ , que é a área clara branca acima à esquerda correspondendo a (A + B ’)’ .

Observe que repetimos, à direita, o AB ’ resultado hachurado duplo de um exemplo anterior para comparação com o nosso resultado. As regiões correspondentes a (A + B ’)’ e AB ’ acima, à esquerda e à direita, respectivamente, são idênticos. Isso pode ser provado com o teorema de DeMorgan e a dupla negação.

Isso traz um ponto. Os diagramas de Venn na verdade não provam nada. A álgebra booleana é necessária para provas formais. No entanto, os diagramas de Venn podem ser usados ​​para verificação e visualização. Verificamos e visualizamos o teorema de DeMorgan com um diagrama de Venn.

Exemplo:

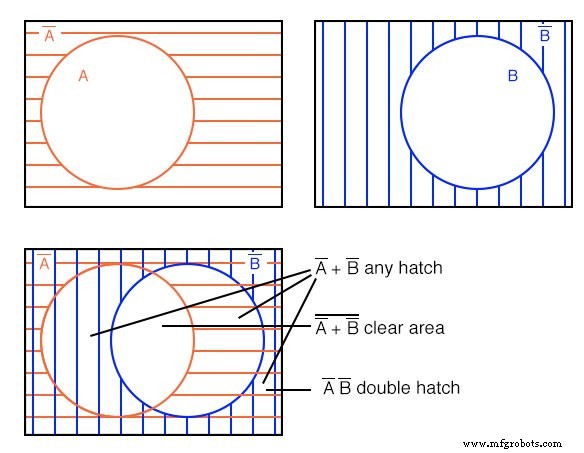
O que significa a expressão booleana A ’+ B’ parece em um diagrama de Venn?



Solução: figura acima

Comece com A ’ tracejado horizontal em vermelho e azul vertical hachurado B ’ acima. Sobreponha os diagramas conforme mostrado. Ainda podemos ver o A ’ hachura horizontal vermelha sobreposta na outra hachura. Também preenche o que costumava fazer parte do B (B-verdadeiro) círculo, mas apenas aquela parte do B círculo aberto não comum ao A círculo aberto.

Se olharmos apenas para o B ’ hachura vertical azul, preenche aquela parte do espaço aberto A círculo não comum a B . Qualquer região com qualquer hachura, independentemente do tipo, corresponde a A ’+ B’ . Ou seja, tudo menos o espaço em branco aberto no centro.

Exemplo:

O que significa a expressão booleana (A ’+ B’) ’ parece em um diagrama de Venn?

Solução: figura acima, esquerda inferior

Olhando para o espaço aberto branco no centro, é tudo NÃO na solução anterior de A ’+ B’ , que é (A ’+ B’) ’ .

Exemplo: Mostre que (A ’+ B’) ’=AB

Solução: figura abaixo, esquerda inferior



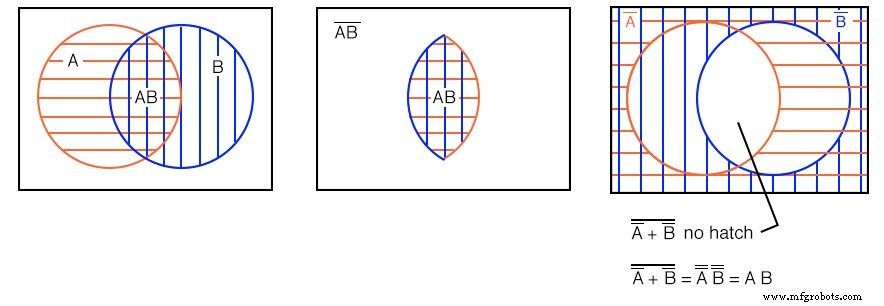
Mostramos anteriormente no diagrama acima à direita que a região branca aberta é (A ’+ B’) ’ . Em um exemplo anterior, mostramos uma região duplamente hachurada na interseção (sobreposição) de AB . Estas são as figuras da esquerda e do meio repetidas aqui.

Comparando os dois diagramas de Venn, vemos que esta região aberta, (A ’+ B’) ’ , é o mesmo que a região duplamente hachurada AB (A AND B). Também podemos provar que (A ’+ B’) ’=AB pelo teorema de DeMorgan e negação dupla como mostrado acima.



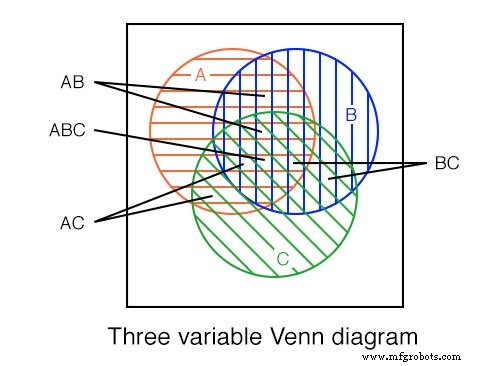
Mostramos um diagrama de Venn de três variáveis ​​acima com as regiões A (vermelho horizontal), B (vertical azul) e, C (verde 45 ^o ) No centro, observe que todas as três regiões se sobrepõem, representando a expressão booleana ABC .

Há também uma região maior em forma de pétala onde A e B sobreposição correspondente à expressão booleana AB . De maneira semelhante A e C sobreposição produzindo expressão booleana AC . E B e C sobreposição produzindo expressão booleana BC .

Olhando para o tamanho das regiões descritas pelas expressões AND acima, vemos que o tamanho da região varia com o número de variáveis ​​na expressão AND associada.

• A , 1 variável é uma grande região circular.
• AB , 2 variáveis ​​é uma região menor em forma de pétala.
• ABC , 3 variáveis ​​é a menor região.
• Quanto mais variáveis ​​no termo AND, menor será a região.