Identidades algébricas booleanas

Em matemática, uma identidade é uma afirmação verdadeira para todos os valores possíveis de sua variável ou variáveis.

A identidade algébrica de x + 0 =x nos diz que qualquer coisa (x) adicionado a zero é igual ao “qualquer coisa” original, não importa o valor que “ qualquer coisa ”(X) pode ser.

Como a álgebra comum, a álgebra booleana tem suas próprias identidades exclusivas com base nos estados bivalentes das variáveis ​​booleanas.

Identidades aditivas

Adicionando Zero

A primeira identidade booleana é que a soma de qualquer coisa e zero é o mesmo que o original “ qualquer coisa . ”

Essa identidade não é diferente de seu equivalente algébrico de número real:







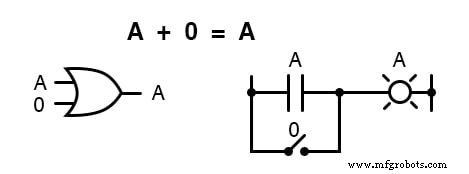
Não importa qual seja o valor de A , a saída será sempre a mesma:quando A =1 , a saída também será 1 ; quando A =0 , a saída também será 0 .

Adicionando um

A próxima identidade é definitivamente diferente de qualquer outra vista na álgebra normal.

Aqui descobrimos que a soma de “ qualquer coisa ”E um é um :







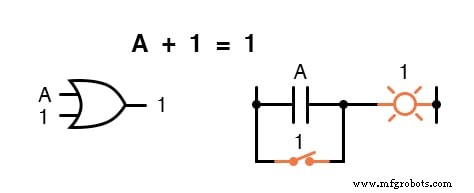
Não importa qual seja o valor de A, a soma de A e 1 sempre será 1.

Em certo sentido, o sinal “1” substitui o efeito de A no circuito lógico, deixando a saída fixa em um nível lógico de 1.

Adicionando uma quantidade a si mesma

A seguir, examinamos o efeito da adição de A e A juntos, o que é o mesmo que conectar as duas entradas de uma porta OU entre si e ativando-os com o mesmo sinal:







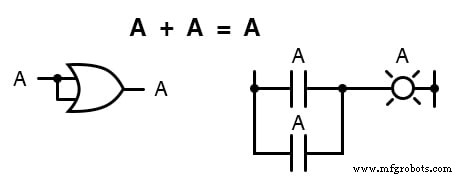
Na álgebra de números reais, a soma de duas variáveis ​​idênticas é duas vezes o valor da variável original (x + x =2 x), mas lembre-se de que não há conceito de “2” no mundo da matemática booleana, apenas 1 e 0, então não podemos dizer que A + A =2A .

Assim, quando adicionamos uma quantidade booleana a si mesma, a soma é igual à quantidade original: 0 + 0 =0 , e 1 + 1 =1 .

Adicionando uma quantidade ao seu complemento

Apresentando o conceito exclusivamente booleano de complementação em uma identidade aditiva, encontramos um efeito interessante.

Uma vez que deve haver um “ 1 ”Valor entre qualquer variável e seu complemento, e como a soma de qualquer quantidade booleana e 1 é 1, a soma de uma variável e seu complemento deve ser 1:

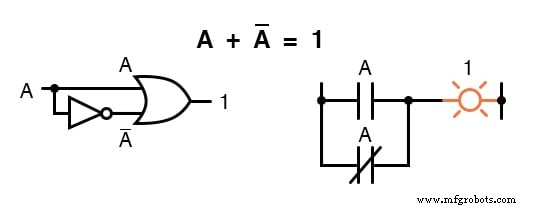
Identidades multiplicativas

Assim como existem quatro identidades aditivas booleanas ( A + 0, A + 1, A + A e A + A ’ ), então também há quatro identidades multiplicativas: Ax0, Ax1, AxA e AxA ’ . Destes, os dois primeiros não são diferentes de suas expressões equivalentes na álgebra regular:

Multiplicando por 0 ou 1

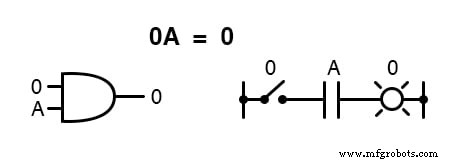
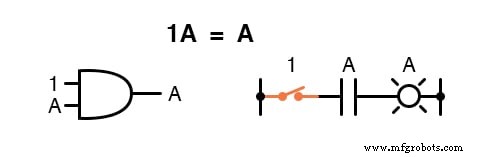
Multiplicando uma quantidade por si mesma

A terceira identidade multiplicativa expressa o resultado de uma quantidade booleana multiplicada por ela mesma.

Na álgebra normal, o produto de uma variável por ele mesmo é o quadrado dessa variável (3 x 3 =3 ² =9).

No entanto, o conceito de quadrado implica em uma quantidade de 2, que não tem significado na álgebra booleana, então não podemos dizer que A x A =A ² .

Em vez disso, descobrimos que o produto de uma quantidade booleana por ele mesmo é a quantidade original, uma vez que 0 x 0 =0 e 1 x 1 =1 :

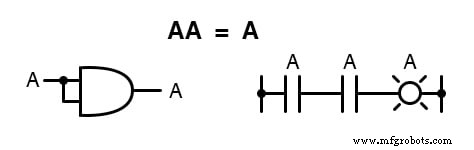
Multiplicando uma quantidade por seu complemento

A quarta identidade multiplicativa não tem equivalente na álgebra regular porque usa o complemento de uma variável, um conceito exclusivo da matemática booleana.

Uma vez que deve haver um “ 0 ”Valor entre qualquer variável e seu complemento, e uma vez que o produto de qualquer quantidade booleana e 0 é 0 , o produto de uma variável e seu complemento deve ser 0 :







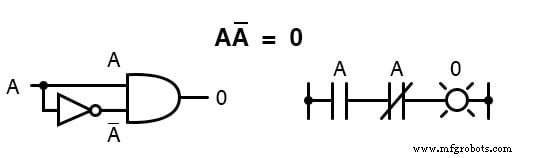
Para resumir, então, temos quatro identidades booleanas básicas para adição e quatro para multiplicação:

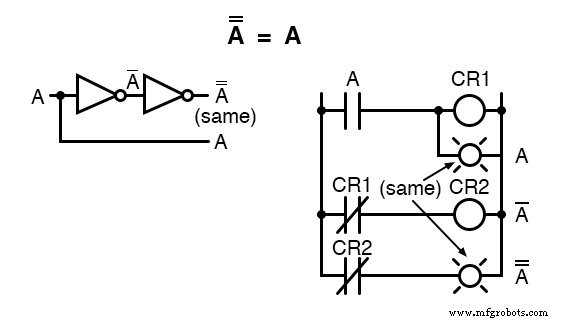
Complemento Duplo

Outra identidade que tem a ver com complementação é a do complemento duplo :uma variável invertida duas vezes.

Complementar uma variável duas vezes (ou qualquer número par de vezes) resulta no valor booleano original.

Isso é análogo a negar (multiplicar por -1) na álgebra de número real:um número par de negações é cancelado para deixar o valor original:







PLANILHAS RELACIONADAS:

• Planilha de álgebra booleana