Efeito da dispersão superficial de elétrons nas proporções de absorção óptica e dispersão para extinção de nanoconcha de ouro

Resumo

A alta dispersão e absorção de luz da nanoconcha de ouro em seu comprimento de onda de ressonância encontraram aplicações em imagens biomédicas e terapia fototérmica. No entanto, em nanoescala, a função dielétrica do material metálico é afetada pelo tamanho das nanopartículas, principalmente por meio de um mecanismo chamado espalhamento de superfície de elétrons de condução. Neste trabalho, o efeito do espalhamento superficial de elétrons nas razões de absorção óptica e espalhamento para extinção (que é a soma da absorção e espalhamento) da nanoconcha de ouro é investigado. Os resultados da simulação para várias espessuras de casca são comparados. Verifica-se que o espalhamento de superfície dos elétrons aumenta a taxa de absorção óptica e quanto mais fina a espessura da casca, maior o aumento na diferença da taxa de absorção entre as situações com e sem o espalhamento de superfície considerado. O aumento da taxa de absorção é então verificado comparando os resultados da simulação com medições experimentais para três nanoconchas. Os parâmetros das simulações para ajuste às medidas experimentais mostram que o amortecimento dos elétrons de condução na geometria da casca metálica é maior do que o previsto pelo modelo de espalhamento de bilhar.

Histórico

A nanoconcha de ouro é composta por um núcleo dielétrico, que pode ser sílica ou Au ₂ S [1, 2] e uma concha concêntrica de ouro. Devido à biocompatibilidade do ouro [3, 4], fácil conjugação de anticorpos e porções de direcionamento à superfície da casca de ouro [5], sintonização de seu comprimento de onda ressonante para a região do infravermelho próximo [2, 6], e uma região chamada janela de água biológica onde a transmissividade do tecido é a mais alta [7], o espalhamento e absorção de luz aprimorados da nanoconcha de ouro encontraram aplicações em imagens biomédicas e terapia fototérmica [8, 9]. A extensão da teoria de Mie para a estrutura núcleo-casca pode ser empregada para calcular a absorção óptica de uma única nanoconcha de ouro e seções transversais de espalhamento [10], e a soma dessas duas fornece sua seção transversal de extinção. Uma vez que a espessura da nanoconcha de ouro é geralmente menor ou comparável ao caminho livre médio do elétron no ouro a granel, que é cerca de 37,7 nm [11], os elétrons na camada de ouro passam por mais colisões por unidade de tempo (colisões extras causadas pelo espalhamento de elétrons de condução da superfície da casca) do que no ouro a granel [12, 13]. O espalhamento de superfície de elétrons de condução foi relatado para causar o alargamento do pico de ressonância, o que foi verificado pelo ajuste de espectros medidos e calculados [6, 14,15,16], e redução nos valores absolutos de ambos espalhamento e absorção de uma única nanoconcha o que foi demonstrado por cálculos teóricos [17,18,19]. No entanto, para aplicações de imagem biomédica com base em espalhamento [9, 20, 21], onde nanopartículas metálicas ou materiais fluorescentes são anexados ao tecido ou células alvo, se for desejado apenas a imagem e não danificar termicamente o tecido ou células sob investigação, É importante que a nanopartícula anexada tenha alta proporção de espalhamento e baixa proporção de absorção no comprimento de onda desejado. A razão pela qual as razões de espalhamento e absorção, mas não seus valores absolutos, são preocupantes é que a diminuição nos valores absolutos de espalhamento e absorção pode ser compensada por ter mais partículas ligadas ao tecido ou células alvo. A aplicação de espalhamento de luz ressonante de nanopartículas metálicas em tela de projeção transparente [22,23,24,25] e em fotovoltaica [26,27,28,29,30], também requer alta dispersão simultânea e taxas de absorção baixas na faixa de comprimento de onda desejada . Além disso, os metamateriais de ouro também exigem que o ouro seja na forma de filme fino, que pode atingir alta absorção óptica como absorvedor de luz [31, 32], ou alta transmitância como filme condutor transparente [33,34,35,36], e, portanto, o efeito de espalhamento de superfície dos elétrons de condução também desempenha um papel. Portanto, pode fornecer alguma orientação sobre o projeto de estrutura relacionada ao ouro em nanoescala para investigar o efeito do espalhamento superficial de elétrons nas razões de absorção óptica e espalhamento para extinção para nanoconchas de ouro.

Neste trabalho, simulações são inicialmente conduzidas para estudar o efeito do espalhamento superficial de elétrons sobre as razões de absorção óptica e espalhamento para extinção de nanoconchas de ouro considerando as situações com e sem o espalhamento superficial. É mostrado que o espalhamento da superfície dos elétrons aumenta a taxa de absorção óptica e, portanto, diminui a taxa de espalhamento de luz e, quanto mais fina a espessura da casca, maior o aumento na taxa de absorção óptica. O aumento da absorção é então verificado experimentalmente para três amostras, comparando sua absorção medida e simulada, bem como espectros de extinção.

A simulação e os resultados experimentais serão mostrados primeiro na seção "Resultados e Discussão" e, em seguida, o método detalhado de medições ópticas de extinção e absorção é fornecido na seção "Métodos / Experimentais", para evitar confusão desnecessária causada pelas descrições de medições ópticas.

Resultados e discussão

Nanoconchas de ouro com quatro espessuras de casca diferentes, mas com o mesmo diâmetro de núcleo, são estudadas por simulação. As nanoconchas de ouro incluem (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 15 nm de espessura), (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 25 nm de espessura), (diâmetro de 80 nm núcleo de sílica) @ (camada de ouro de 35 nm de espessura) e (núcleo de sílica de 80 nm de diâmetro) @ (camada de ouro de 45 nm de espessura).

Após a interação de raios de luz incidentes paralelos com uma única nanopartícula, além daqueles transmitidos diretamente (propagando-se na direção original da luz incidente), a luz é absorvida ou espalhada, e a soma desses dois é referida como extinção [37 ] O espalhamento, absorção e extinção, quantizados em termos de seções transversais, que podem ser intuitivamente percebidos como a quantidade de área de luz removida do caminho da luz incidente devido ao espalhamento, absorção ou extinção, respectivamente, podem ser calculados pela extensão da teoria de Mie. para estrutura core-shell [10]. No entanto, é mais natural normalizar as seções transversais para a seção transversal geométrica da nanopartícula, πR ² , onde R é o raio externo de uma estrutura núcleo-casca, para fins de comparação entre diferentes estruturas, e a proporção de j seção transversal ( j =absorção, espalhamento ou extinção) para a seção transversal geométrica é denominado como j eficiência.

As eficiências de extinção e absorção sem consideração do efeito de espalhamento da superfície são calculadas usando a função dielétrica do ouro em massa [38] como entrada para a teoria de Mie, e são mostradas como linhas vermelhas (sólidas ou tracejadas) na Fig. 1. Para levar em consideração o efeito de espalhamento de superfície, assume-se que a função dielétrica do ouro tem um componente do modelo Drude para descrever o comportamento dos elétrons livres [39], e um termo de amortecimento extra γ _s contribuído pelo espalhamento superficial de elétrons de condução é adicionado ao amortecimento em massa γ _b no termo Drude para dar a função dielétrica corrigida ε _sh para casca de ouro [19]:
$$ {\ varejpsilon} _ {\ mathrm {s} \ mathrm {h}} ={\ varejpsilon} _ {\ mathrm {exp}} + \ frac {\ omega _ {\ mathrm {p}} ^ 2} {\ omega \ left (\ omega + i {\ gamma} _ {\ mathrm {b}} \ right)} - \ frac {\ omega _ {\ mathrm {p}} ^ 2} {\ omega \ left [\ omega + i \ Big ({\ gamma} _ {\ mathrm {b}} + {\ gamma} _ {\ mathrm {s}} \ right]} $$ (1)
onde ε _exp é a função dielétrica em massa do ouro da referência [38], ω _p é a frequência de plasma do ouro, ω é a frequência da luz incidente, e i é o número imaginário. Para as eficiências calculadas com efeito de espalhamento de superfície na Fig. 1 (linhas azuis, sólidas ou tracejadas), ω _p e γ _b são assumidos como sendo 8,55 eV e 18,4 meV, respectivamente [19]. E γ _s é dado por [19]:
$$ {\ gamma} _ {\ mathrm {s}} =\ frac {v _ {\ mathrm {F}}} {L _ {\ mathrm {B}}} $$ (2)
onde v _F é a velocidade de Fermi dos elétrons no ouro e é igual a 1,40 × 10 ⁶ m / s [19] e L _B é o caminho livre médio efetivo dos elétrons na camada, derivado assumindo o modelo de espalhamento de bilhar [13], no qual as reflexões dos elétrons das duas superfícies da camada são especulares, e é dado por
$$ {L} _B =\ frac {4 \ left ({r} _ {\ mathrm {o}} ^ 3- {r} _ {\ mathrm {i}} ^ 3 \ right)} {3 \ left ( {r} _ {\ mathrm {o}} ^ 2+ {r} _ {\ mathrm {i}} ^ 2 \ direita)} $$ (3)
onde r _o e r _i são os raios externo e interno da nanoconcha, respectivamente. Os índices de refração do meio circundante e do núcleo de sílica são considerados 1,5 e 1,45, respectivamente.

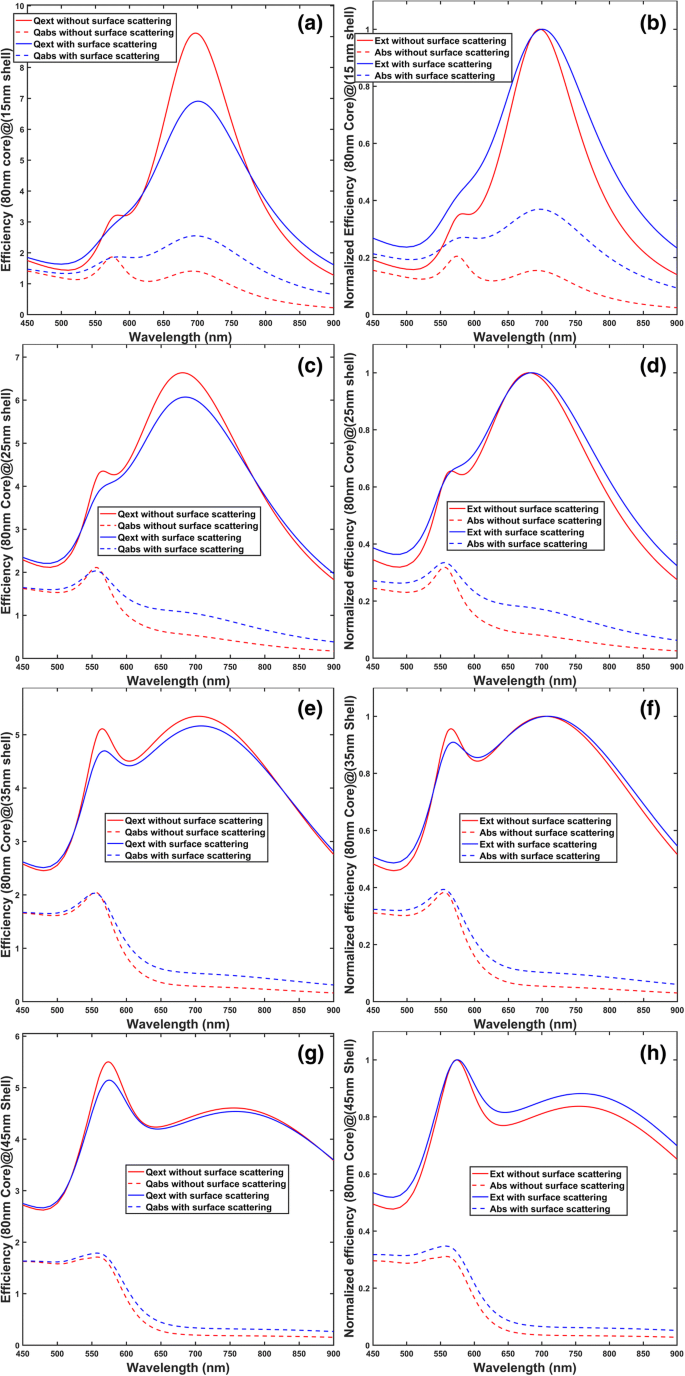
Extinção calculada e eficiências de absorção com e sem consideração de espalhamento superficial de elétrons de condução, onde Q _ext (Ext) significa eficiência de extinção (extinção normalizada) e Q _abs (Abs) significa eficiência de absorção (absorção normalizada). A eficiência de espalhamento (espalhamento normalizado) é a diferença entre o Q _ext (Ext) e Q _abs (Abdômen). Todos os cálculos são realizados pela teoria de Mie, com índices de sílica e meio circundante assumidos como 1,45 e 1,5, respectivamente. As constantes dielétricas de ouro sem espalhamento de superfície são da referência [38], enquanto aquelas com espalhamento de superfície são dadas pelas Eqs. (1) ~ (3) . a e b são para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 15 nm de espessura). c e d são para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 25 nm de espessura). e e f são para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 35 nm de espessura). g e h são para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 45 nm de espessura). A coluna da esquerda, ou seja, a , c , e , e g , são as eficiências correspondentes calculadas pela teoria de Mie. A coluna certa, ou seja, b , d , e f , é a eficiência normalizada para o pico de ressonância dipolar (o pico de ressonância entre 700 e 800 nm), e h as eficiências normalizadas para o pico de ressonância quadrupolar (o pico entre 550 e 600 nm)

Na coluna da esquerda da Fig. 1, para as quatro espessuras de casca, após incluir o efeito de espalhamento de superfície, observa-se que ambos os espectros de extinção e absorção experimentam um alargamento e que, enquanto os espectros de extinção diminuem em magnitude, os espectros de absorção aumentam lote no pico de ressonância dipolar (o pico entre 700 e 800 nm) e parece não mudar no pico de ressonância quadrupolar (o pico entre 550 e 600 nm). A diminuição na magnitude da eficiência de extinção e o aumento na magnitude da eficiência de absorção levam a um aumento na razão de absorção para extinção, após a inclusão do efeito de espalhamento de superfície. Isto é confirmado pela coluna direita da Fig. 1, onde se observa que a absorção aumenta (isto é, as linhas tracejadas azuis estão acima das linhas tracejadas vermelhas) nas posições de pico dipolar e quadrupolar. Intuitivamente, o aumento na taxa de absorção após considerar o efeito de espalhamento da superfície torna-se menos significativo com o aumento da espessura da casca, como pode ser observado em (b), (d), (f) e (h) na Fig. 1. Isso ocorre porque o quanto mais espessa a camada, menor será a frequência das colisões de elétrons com as superfícies da camada, ou seja, o efeito de espalhamento da superfície é reduzido. O fenômeno também é confirmado pela Tabela 1. Para cada espessura de casca, a taxa de absorção com (sem) espalhamento de superfície, calculada pela razão da região sob a curva tracejada azul (vermelha) para a região sob a curva sólida azul (vermelha) , está tabulado na Tabela 1. Para investigar melhor o mecanismo por trás do aumento da razão de absorção, as distribuições espaciais do quadrado da amplitude do campo elétrico próximo | E | ² são plotados na Fig. 2. Na Fig. 2, pode-se observar que | E | ² s calculados sem espalhamento de superfície são maiores do que aqueles com espalhamento de superfície, o que pode ser explicado desta forma:assumindo que o espalhamento de superfície tenha efeito, os elétrons de condução experimentam mais colisões de superfícies de casca em comparação com aqueles em ouro a granel, então a amplitude média de oscilação dos elétrons de condução é diminuiu, levando a redução | E | ² s . E como as colisões de elétrons de condução com as superfícies da camada contribuem para a perda de energia na forma de calor, a taxa de absorção aumenta após incluir o efeito de espalhamento na superfície.

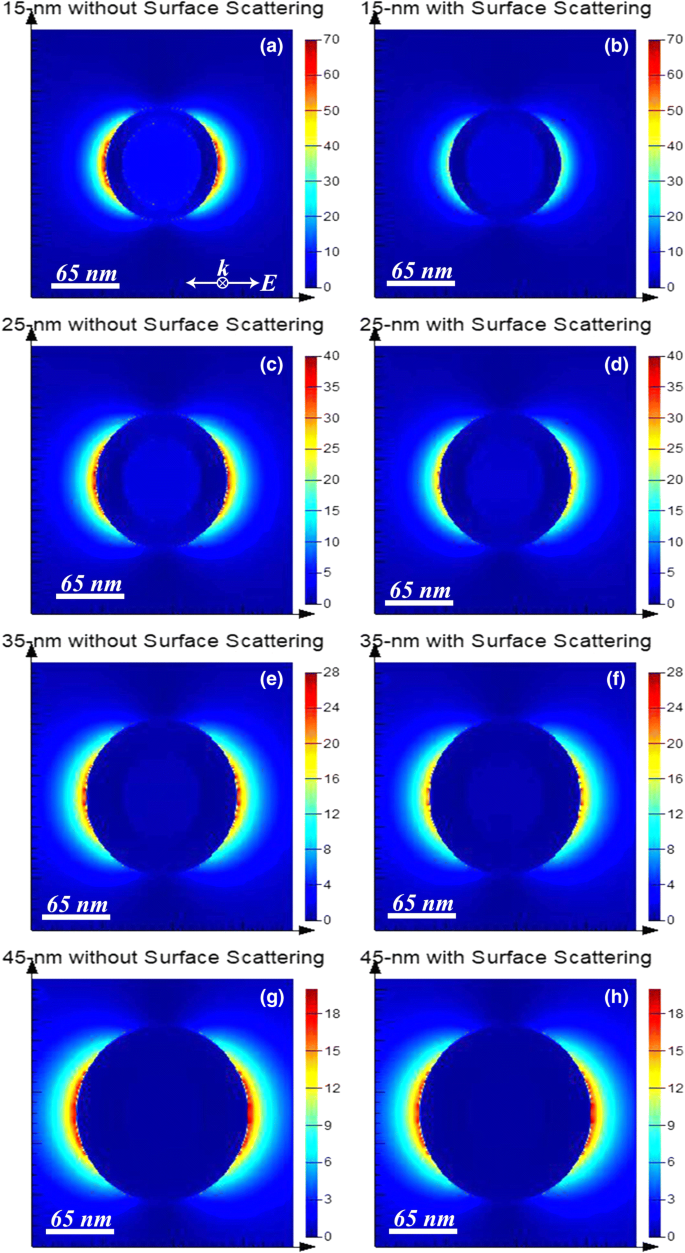
Quadrado da amplitude do campo elétrico próximo | E | ² gráficos das quatro estruturas mostradas na Fig. 1 em seus comprimentos de onda de pico de ressonância dipolar correspondentes. a e b são representados graficamente para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 15 nm de espessura) a 700 nm. c e d são traçados para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 25 nm de espessura) a 684 nm. e e f são traçados para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 35 nm de espessura) a 706 nm. g e h são representados graficamente para (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 45 nm de espessura) a 756 nm. A coluna da esquerda, ou seja, a , c , e , e g , mostra | E | ² calculado com as constantes dielétricas do ouro a granel da referência [38]. A coluna certa, ou seja, b , d , f , e h , mostra | E | ² calculado com constantes dielétricas de ouro modificadas com espalhamento de superfície via Eqs. (1) ~ (3). A polarização e a direção de propagação da luz incidente são as mesmas para todas as figuras e são mostradas em a . A simulação é conduzida pelo software "FDTD Solutions", com o tamanho da grade da região de substituição da malha tridimensional sendo 1 nm

Sujeito à disponibilidade de material, a absorção e extinção são experimentalmente medidas para três nanoconchas de diferentes espessuras de concha, mas diâmetros de núcleo semelhantes:(núcleo de sílica de 80 nm de diâmetro) @ (concha de ouro de 16 nm de espessura), (79 nm de diâmetro núcleo de sílica) @ (casca de ouro de 29 nm de espessura) e (núcleo de sílica de 88 nm de diâmetro) @ (casca de ouro de 36 nm), cujas imagens TEM são mostradas na Fig. 3. A Figura 4 mostra a comparação entre os resultados medidos experimentalmente e simulados teoricamente para as três nanoconchas. Pode-se observar na Fig. 4 que as seções transversais de absorção calculadas com o efeito de espalhamento de superfície levado em consideração concordam bem com os resultados medidos para todas as três nanoconchas, embora haja um grande afastamento entre as absorções medidas e simuladas se a superfície efeito de espalhamento não é considerado.

Imagens TEM das três nanoconchas de ouro usadas em medições experimentais. a Núcleo de sílica de 80 nm de diâmetro, casca de ouro de 16 nm de espessura. b Núcleo de sílica de 79 nm de diâmetro, casca de ouro de 29 nm de espessura. c Núcleo de sílica de 88 nm de diâmetro, casca de ouro de 36 nm de espessura. As informações detalhadas de caracterização são fornecidas em informações de apoio

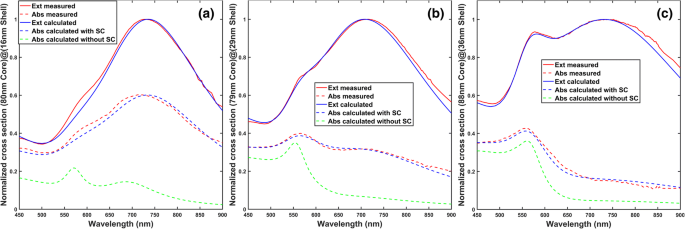
Comparações entre espectros de absorção medidos e calculados com e sem consideração de espalhamento de superfície de elétrons de condução. Todos os cálculos são realizados pela teoria de Mie. O meio circundante é PVA (álcool polivinílico) com um índice de refração de 1,5. Observe que o meio circundante de nanoconchas em nosso experimento (PVA, n =1,5) é diferente daquela na ficha de caracterização fornecida na informação de apoio, que é a água. Os surfactantes que revestem as nanoconchas podem ser desprezados porque os surfactantes são polímeros finos e têm índice de refração semelhante ao meio circundante de PVA. O índice de refração da sílica é considerado 1,45 nos cálculos. As constantes dielétricas de ouro sem espalhamento de superfície são da referência [38], enquanto aquelas com espalhamento de superfície são dadas pelas Eqs. (1) e (4). Em todas as legendas das figuras, “Ext” é a abreviatura de extinção, “Abs” é a abreviatura de absorção e “SC” é a abreviatura de espalhamento de superfície. Em cada figura, "Ext calculado" e "Abs calculado com SC" são os espectros de extinção e absorção calculados com os parâmetros de ajuste mostrados na Tabela 2, enquanto "Abs calculado sem SC" é a seção transversal de absorção calculada sem considerar a distribuição de tamanho e superfície espalhamento. a (Núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 16 nm de espessura). b (Núcleo de sílica de 79 nm de diâmetro) @ (casca de ouro de 29 nm de espessura). c (Núcleo de sílica de 88 nm de diâmetro) @ (casca de ouro de 36 nm de espessura)

Para ajustar as extinções calculadas (as linhas azuis sólidas) às extinções medidas experimentalmente (as linhas vermelhas sólidas), que são mostradas na Fig. 4, a expressão do amortecimento extra γ _s na Eq. (1) devido ao espalhamento da superfície é dado pela Eq. (4) mostrado abaixo [15], em vez da Eq. (2)
$$ {\ gamma} _ {\ mathrm {s}} =\ frac {A {v} _ {\ mathrm {F}}} {d _ {\ mathrm {s}}} $$ (4)
onde A é um parâmetro de ajuste adimensional e um A maior indica um amortecimento maior e d _s é a espessura da casca. O parâmetro de ajuste A é afetado por muitos fatores:densidade de elétrons na superfície, efeito da interface, anisotropia de partícula e computação mecânica quântica, e seu valor foi mostrado na faixa de 0,1 a acima de 2 [40, 41]. Observe que podemos escrever a Eq. (2) na forma da Eq. (4) para comparar o valor teórico de A previsto pelo modelo de espalhamento de bilhar para aqueles ajustados a partir do experimento, calculando primeiro o valor de L _B na Eq. (2) usando a Eq. (3) e, em seguida, escrevendo L _B na Eq. (2) na forma de d _s / A , conforme mostrado na Eq. (5a) a (5d) abaixo:
$$ {\ gamma} _ {\ mathrm {s}} =\ frac {v _ {\ mathrm {F}}} {L _ {\ mathrm {B}}} ={v} _ {\ mathrm {F}} \ bullet \ frac {3 \ left ({r} _ {\ mathrm {o}} ^ 2+ {r} _ {\ mathrm {i}} ^ 2 \ right)} {4 \ left ({r} _ {\ mathrm {o}} ^ 3- {r} _ {\ mathrm {i}} ^ 3 \ right)} $$ (5a)
escrever
$$ \ frac {3 \ left ({r} _ {\ mathrm {o}} ^ 2+ {r} _ {\ mathrm {i}} ^ 2 \ right)} {4 \ left ({r} _ { \ mathrm {o}} ^ 3- {r} _ {\ mathrm {i}} ^ 3 \ right)} =\ frac {A} {d _ {\ mathrm {s}}} $$ (5b)
então
$$ {\ gamma} _ {\ mathrm {s}} =\ frac {A {v} _ {\ mathrm {F}}} {d _ {\ mathrm {s}}} $$ (5c)
Onde
$$ A ={d} _ {\ mathrm {s}} \ bullet \ frac {3 \ left ({r} _ {\ mathrm {o}} ^ 2+ {r} _ {\ mathrm {i}} ^ 2 \ right)} {4 \ left ({r} _ {\ mathrm {o}} ^ 3- {r} _ {\ mathrm {i}} ^ 3 \ right)} $$ (5d)
Observe que quando a espessura da casca é menor que 25% do raio total, a Eq. (5d) dá um A valor de cerca de 0,5 [13]. Os valores dos parâmetros de ajuste para os espectros calculados das três nanoconchas mostradas na Fig. 4 são tabulados na Tabela 2.

Os espectros de extinção e absorção calculados mostrados na Fig. 4, que são normalizados para o pico dipolar, consideraram o espalhamento da superfície e a distribuição de tamanho. Para cada nanoconcha, os desvios padrão do diâmetro do núcleo e da espessura da casca são calculados, respectivamente, multiplicando os valores do diâmetro do núcleo e da espessura da casca mostrados na Tabela 2 com o coeficiente de variação dado nas folhas de caracterização fornecidas nas informações de suporte. Os diâmetros centrais usados na conexão são maiores do que os valores fornecidos nas folhas de caracterização. Isso ocorre porque o tamanho da esfera de sílica diminui sob exame de TEM [42, 43], e as espessuras de casca são obtidas subtraindo os diâmetros do núcleo na Tabela 2 dos diâmetros totais dados nas folhas de caracterização. As larguras de pico dos espectros de extinção calculados são ajustados para coincidir com os medidos e, em seguida, os espectros de absorção correspondentes são calculados com os parâmetros ajustados. Os valores de A previsto pelo modelo de espalhamento de bilhar seria 0,60, 0,52 e 0,53 para as três nanoconchas, respectivamente, se a Eq. (5d) é aplicado, que são obviamente menores do que o A ajustado valores listados na Tabela 2, que são 1,33, 1,67 e 1,33, respectivamente para as três nanoconchas. Já que um valor maior de A na Eq. (4) significa um amortecimento maior de elétrons livres, observa-se que o amortecimento real de elétrons de condução é maior do que o previsto pelo modelo de espalhamento de bilhar, onde o amortecimento extra pode ser devido à interface química entre a casca e o meio circundante bem como o núcleo de sílica [44, 45], densidade de elétrons na superfície, anisotropia de partícula e computação mecânica quântica, como mencionado anteriormente. A possibilidade de casca descontínua pode ser excluída observando a imagem TEM na folha de caracterização nas informações de apoio. Observe que o pico de alargamento devido à distribuição do tamanho da nanoconcha já foi considerado durante o ajuste, ou seja, os valores ajustados de A não leva em conta a distribuição de tamanho. Os detalhes de como medir a extinção e absorção são descritos na seção “Métodos / Experimental”.

Métodos / Experimental

Nesta seção, para as nanoconchas estudadas na Fig. 4, é descrito como dispersá-las em filmes finos de PVA (álcool polivinílico) e como derivar a extinção e absorção dessas nanoconchas de medições ópticas dos filmes finos de PVA dispersos em nanopartículas.

As três nanoconchas estudadas na Fig. 4, ou seja, (núcleo de sílica de 80 nm de diâmetro) @ (casca de ouro de 16 nm de espessura), (núcleo de sílica de 79 nm de diâmetro) @ (casca de ouro de 29 nm de espessura) , e (núcleo de sílica de 88 nm de diâmetro) @ (casca de ouro de 36 nm de espessura), que por conveniência são abreviados como nanoconchas de ouro de 16 nm, 29 nm e 36 nm, respectivamente na discussão a seguir, foram adquiridos diretamente de uma empresa especializada, nanoComposix, e suas fichas de caracterização são apresentadas nas informações de apoio (arquivo adicional 1).

As nanoconchas foram dispersas em água após o recebimento, com a nanoconcha de ouro de 16 nm tendo uma concentração de 0,02 mg / mL e as outras duas tendo uma concentração de 0,05 mg / mL. Para as nanoconchas de ouro de 16 nm, 29 nm e 36 nm, 34, 25 e 34 mL de suas soluções foram usados para fazer o filme de PVA disperso em nanopartículas. Antes de misturar as soluções de nanoconcha conforme recebidas com pó de PVA (80% hidrolisado, Sigma-Aldrich), cada solução de nanoconcha foi concentrada a 9 mL por centrifugação e redispersão. E então 0,9 g de pó de PVA foi adicionado a cada solução de nanoconcha concentrada e as misturas foram agitadas durante 2 h. Depois disso, cada solução agitada foi removida da bolha em uma câmara de vácuo e, em seguida, vertida em um ² de 5 × 5 cm molde de vidro, e o molde foi colocado em uma capela para deixar a solução secar naturalmente. Depois que as soluções foram secas, os filmes de PVA foram arrancados dos moldes de vidro e são mostrados na Fig. 5. Um filme de PVA puro sem nenhuma nanopartícula dispersa foi feito da mesma forma, exceto que 9 mL de água em vez de solução de nanoconcha foram misturados com PVA em pó.

a Filme disperso com a nanoconcha de ouro de 16 nm. b Filme disperso com a nanoconcha de ouro de 29 nm. c Filme disperso com a nanoconcha de ouro de 36 nm. d Filme PVA puro

A seção transversal de extinção σ _ext de uma nanoconcha está ligada à transmitância direta T de uma película fina de nanoconchas através da lei de Beer-Lambert [44]:
$$ T ={e} ^ {- N \ bullet {\ sigma} _ {\ mathrm {ext}}} $$ (6)
onde N é a densidade de área de nanopartículas, ou seja, o número de nanoconchas por unidade de área (observe que esta área é perpendicular à direção de propagação da luz incidente). A transmitância direta T é obtido normalizando a transmitância direta medida de um filme de PVA disperso com nanoconcha para aquele do filme de PVA puro sem qualquer nanopartícula dispersa. Então N ∙ σ _ext é dado pela seguinte equação:
$$ N \ bullet {\ sigma} _ {\ mathrm {ext}} =- \ ln (T) $$ (7)
Observe que em vez de σ _ext , apenas N ∙ σ _ext é derivado de medições experimentais, porque é a forma geral do espectro que importa. Na Fig. 4, N ∙ σ _ext é normalizado de forma que o valor máximo de N ∙ σ _ext do espectro é 1.

A seção transversal de absorção σ _abs de uma única nanoconcha está relacionada à perda de intensidade de um feixe paralelo de luz incidente devido à absorção ∆I _abs após passar por uma fina película de nanopartículas, com base na lei de Beer-Lambert [44]:
$$ \ Delta {I} _ {\ mathrm {abs}} ={I} _0 \ left (1- {e} ^ {- N \ bullet {\ sigma} _ {\ mathrm {abs}}} \ right) $$ (8)
onde eu ₀ é a intensidade da luz incidente.

Portanto, a próxima etapa é encontrar experimentalmente a atenuação da luz incidente apenas devido à absorção das nanopartículas. A equação (8) assume que a partícula é puramente absorvente [44]. Para nanopartículas que absorvem e espalham luz simultaneamente, a Eq. (8) não é válido por causa de absorções múltiplas. Para um conjunto dessas nanopartículas, quando a luz incidente atinge a nanopartícula pela primeira vez, alguns raios de luz são absorvidos e alguns são espalhados. Mas para esses raios de luz dispersos, quando eles atingem mais nanopartículas durante seu caminho para fora do conjunto das nanopartículas, uma parte deles é absorvida novamente, levando a múltiplas absorções. Múltiplas absorções da luz espalhada sugerem que, medindo a quantidade total de luz que não é absorvida pelo filme PVA disperso com nanoconchas, o N ∙ σ _abs derivado de acordo com a Eq. (8) tende a superestimar a absorção. No entanto, uma vez que o filme de PVA em nossos experimentos é fino (cerca de 0,3 mm) e a concentração de nanoconchas não é alta, presume-se que a maior parte da luz sofre espalhamento único (e, portanto, absorção única) [25]. Com esta suposição, a configuração experimental usando uma esfera de integração para medir a quantidade total de luz que não é absorvida pelo filme PVA disperso com nanoconchas é mostrado na Fig. 6. Na Fig. 6 T ₁ , T ₂ , ou R é proporcional à quantidade de luz presa na esfera de integração, ou seja, a quantidade de luz que não sai pela porta aberta no lado direito. Na discussão a seguir, presume-se que T ₁ , T ₂ , e R são proporcionais à intensidade da luz coletada pela esfera integradora com o mesmo coeficiente α .

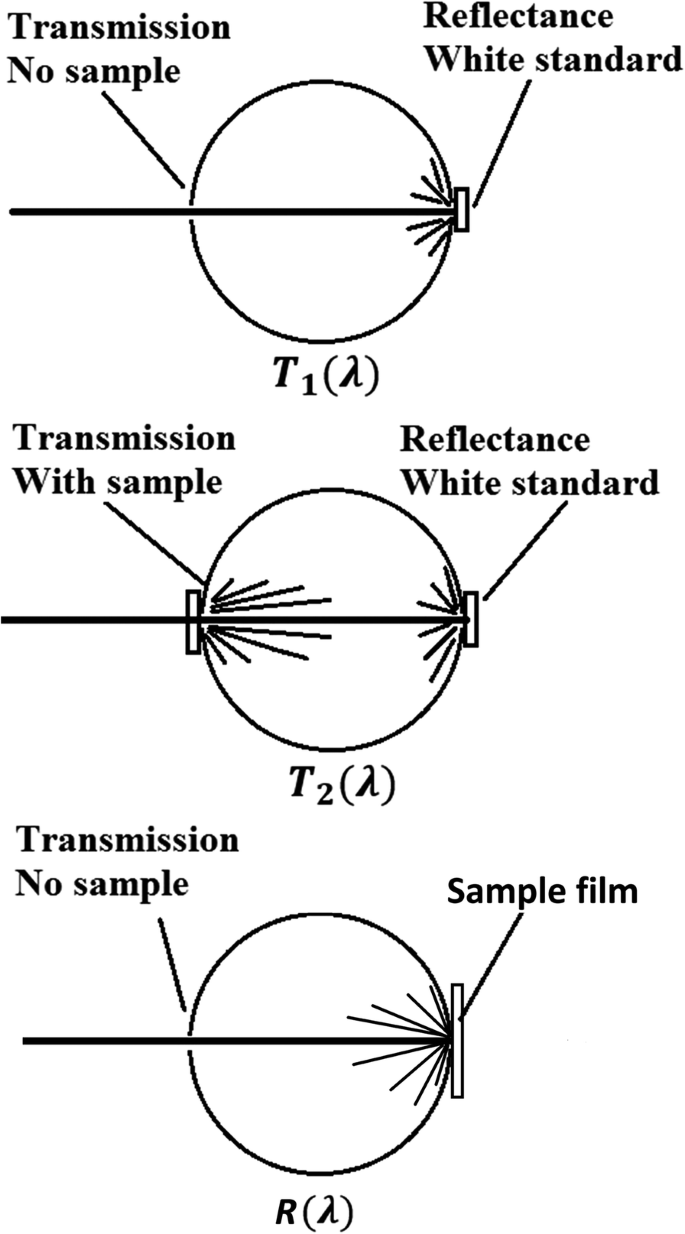
Configuração experimental para medir a absorção. Os valores medidos diretamente são T ₁ ( λ ), T ₂ ( λ ), e R ( λ ) onde T _i ( eu =1, 2) ou R ( λ ) é proporcional à quantidade de luz presa na esfera de integração. A absorção é deduzida desses valores medidos. Esta configuração é uma versão simplificada daquela relatada na referência [22]

A equação (8) pode ser reorganizada em \ (\ left ({I} _0- \ Delta {I} _ {\ mathrm {abs}} \ right) ={I} _0 {e} ^ {- N \ bullet {\ sigma} _ {\ mathrm {abs}}} \), e seu lado esquerdo representa a quantidade total de luz que não é absorvida depois que a luz incidente passa pelo filme de amostra. A partir das medições na Fig. 6, podemos escrever as seguintes equações:
$$ \ left ({I} _0- \ Delta {I} _ {\ mathrm {abs}} \ right) =\ upalpha \ left ({T} _2 \ left (\ lambda \ right) + R \ left (\ lambda \ right) \ right) $$ (9) $$ {I} _0 =\ upalpha {T} _1 \ left (\ lambda \ right) $$ (10)
Substituindo a Eq. (9) e Eq. (10) em \ (\ left ({I} _0- \ Delta {I} _ {\ mathrm {abs}} \ right) ={I} _0 {e} ^ {- N \ bullet {\ sigma} _ { \ mathrm {abs}}} \), e incluindo um termo de ruído além de N ∙ σ _abs , a seguinte equação pode ser obtida:
$$ \ frac {T_2 \ left (\ lambda \ right) + R \ left (\ lambda \ right)} {T_1 \ left (\ lambda \ right)} ={e} ^ {- \ left (N \ bullet { \ sigma} _ {\ mathrm {abs}} + ruído \ right)} $$ (11)
onde Ruído é da matriz PVA. Devido à primeira reflexão da luz incidente na interface ar / PVA, cerca de 4% da luz incidente nunca entra na película fina (de acordo com as equações de Fresnel, na incidência normal em uma interface de dois meios de índices diferentes n ₁ (=1 para ar) e n ₂ (=1,5 para PVA), a refletância da luz R é dado por \ (R ={\ left | \ frac {n_1- {n} _2} {n_1 + {n} _2} \ right |} ^ 2 \)) e, portanto, a Eq. (11) é modificado como
$$ \ frac {T_2 \ left (\ lambda \ right) + R \ left (\ lambda \ right) -0,04 {T} _1 \ left (\ lambda \ right)} {T_1 \ left (\ lambda \ right) - 0,04 {T} _1 \ left (\ lambda \ right)} ={e} ^ {- \ left (N \ bullet {\ sigma} _ {\ mathrm {abs}} + Ruído \ right)} $$ (12)
Assumindo o Ruído no filme de PVA puro sem qualquer nanopartícula dispersa é o mesmo que nos filmes dispersos de nanoconcha, uma expressão semelhante pode ser derivada para o filme de PVA puro:
$$ \ frac {T_2 ^ {\ prime} \ left (\ lambda \ right) + {R} ^ {\ prime} \ left (\ lambda \ right) -0,04 {T} _1 \ left (\ lambda \ right) } {T_1 \ left (\ lambda \ right) -0,04 {T} _1 \ left (\ lambda \ right)} ={e} ^ {- Ruído} $$ (13)
onde \ ({T} _2 ^ {\ prime} \ left (\ lambda \ right) \) e R ^′ ( λ ) são medidos para o filme PVA puro da mesma forma que T ₂ ( λ ) e R ( λ ) para o filme disperso em nanoconcha, respectivamente.

Das Eqs. (12) e (13), N ∙ σ _abs é dado pela seguinte expressão:
$$ N \ bullet {\ sigma} _ {\ mathrm {abs}} =- \ ln \ left (\ frac {T_2 \ left (\ lambda \ right) + R \ left (\ lambda \ right) -0,04 {T } _1 \ left (\ lambda \ right)} {T_2 ^ {\ prime} \ left (\ lambda \ right) + {R} ^ {\ prime} \ left (\ lambda \ right) -0,04 {T} _1 \ esquerda (\ lambda \ direita)} \ direita) $$ (14)
No entanto, durante o ajuste aos resultados experimentais, em que o valor de A na Eq. (4) é ajustado de modo que a largura do pico do espectro de extinção calculado se ajuste ao medido, verifica-se que o N normalizado ∙ σ _abs ainda é um pouco maior do que a absorção calculada, que inclui o efeito de espalhamento de superfície. Isso sugere que a absorção múltipla de luz espalhada ainda pode contribuir para a absorção extra, conforme discutido anteriormente. Portanto, estima-se aqui que uma parcela p (0 < p < 1) of the scattered light when no multiple absorptions happen is absorbed in the actual situation, where p is estimated to be 10% for the 16-nm nanoshell and 5% for both the 29 nm and 36 nm. The following two equations are set to account for the multiple scattering effect:
$$ N\bullet {\sigma_{\mathrm{abs}}}^{\prime }+N\bullet {\sigma_{\mathrm{sca}}}^{\prime }=N\bullet {\sigma}_{\mathrm{ext}} $$ (15) $$ N\bullet {\sigma}_{\mathrm{abs}}+\left(1-p\right)N\bullet {\sigma_{\mathrm{sca}}}^{\prime }=N\bullet {\sigma}_{\mathrm{ext}} $$ (16)
where N ∙ σ _abs ^′ e N ∙ σ _sca ^′ are the light absorption and scattering, respectively, when no multiple absorptions happen, and N ∙ σ _abs e N ∙ σ _ext are the experimentally measured absorption and extinction given by Eq. (14) and Eq. (7) respectively. The extinction in Eqs. (15) and (16) is the same because multiple scattering does not induce error in the measurement of N ∙ σ _ext . From Eqs. (15) and (16), the corrected expression for the measured absorption is given below:
$$ N\bullet {\sigma_{\mathrm{abs}}}^{\prime }=N\bullet {\sigma}_{\mathrm{ext}}-\frac{1}{\left(1-p\right)}\left(N\bullet {\sigma}_{\mathrm{ext}}-N\bullet {\sigma}_{\mathrm{abs}}\right) $$ (17)
In Fig. 4, the corrected absorption N ∙ σ _abs ^′ is also normalized to the maximum value of the N ∙ σ _ext spectrum calculated with Eq. (7).

Conclusões

In this work, surface scattering of conduction electrons in gold nanoshell is shown to not only broaden the extinction peak width, but also increase the ratio of light absorption to extinction and thus decrease the ratio of light scattering to extinction. It is also found that the thinner the shell thickness, the more increase of the absorption ratio. And the increase of light absorption ratio is verified by fitting of calculated absorption spectra to measured ones.

Propriedades eletrônicas ajustáveis por deformação e alinhamentos de banda na heteroestrutura GaTe / C2N:um cálculo dos primeiros princípios Ressonância de plasma na fotoabsorção de nanocristais de ZnO coloidais altamente dopados

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias