Ressonância de plasma na fotoabsorção de nanocristais de ZnO coloidais altamente dopados

Resumo

Um novo tipo de excitações de plasmão dipolo em nanocristais de ZnO coloidais altamente dopados foi estudado por meio da abordagem da mecânica quântica de muitos corpos. Demonstramos que em nanocristais de ZnO fotodopados, os elétrons da banda de condução estão localizados próximos à superfície e as oscilações do plasmon são induzidas por seu movimento angular. A transição desse modo plasmon do regime clássico para o quântico é definida pelo tamanho do nanocristal. A dependência do tamanho da frequência de ressonância que resulta dos efeitos quânticos está em notável acordo com as observações experimentais.

Histórico

Em grande medida, as propriedades ópticas das nanopartículas são determinadas pela presença de ressonâncias plasmônicas de superfície localizadas (LSPR) em seus espectros de excitação [1-8]. Kriegel et al. [2] publicou uma visão geral bastante detalhada de nanocristais coloidais (NCs) emergentes, incluindo NCs de óxido de metal dopado com impureza, NCs de calcogeneto de cobre e NCs de semicondutores dopados degenerativamente, e discutiu extensivamente suas propriedades ópticas, bem como aplicações para detecção de campo próximo aprimoramento da espectroscopia, dispositivos optoeletrônicos sintonizáveis ou aplicações biomédicas. Todos esses novos materiais são uma alternativa aos NCs de metais nobres que foram amplamente estudados nas últimas décadas; para uma revisão abrangente, consulte também a Ref. [9]. Foi demonstrado que é possível ajustar a resposta óptica de nanocristais semicondutores (NCs) fortemente dopados para a faixa de IR [10-15], agindo em vários parâmetros de controle [11, 13, 16-20], abrindo assim novas perspectivas para a nanofotônica. A principal vantagem dos NCs de semicondutores é que a densidade da portadora pode ser ajustada em um amplo intervalo. Considerando que um condutor metálico tem uma densidade fixa de elétrons, um semicondutor pode ser dopado para atingir densidades de portadores arbitrárias em uma faixa de 10 ¹⁶ ÷ 10 ²² cm ⁻³ [10, 13, 21, 22]. O dopagem de portadora permite o acesso ao LSPR sintonizável em uma ampla faixa de frequência de THz a IR e região visível [13]. Tal capacidade de ajuste de densidade de portador é uma propriedade única de nanopartículas semicondutoras e não pode ser alcançada usando gotículas metálicas [23-25]. O doping pode ser feito incorporando vários tipos de impurezas na rede cristalina [7, 10, 18], e a frequência de ressonância do plasmon pode ser ajustada ou trocada pelo controle ativo de portadores [13, 16-18, 21, 22]. Além disso, a frequência do plasmon e sua forma de linha dependem não apenas da densidade do portador do NC, mas do tipo de dopagem, que pode ser "semelhante à massa" ou "semelhante à superfície" [15, 22]. No primeiro caso, a carga de portadores livres é neutralizada pela carga de impurezas de dopagem em todo o volume de NC, enquanto no último caso, os portadores livres são injetados no volume de NC por doadores / aceitadores do meio circundante localizado no Interface NC.

Estudos teóricos da resposta óptica de nanopartículas semicondutoras revelaram diferenças significativas entre a mecânica quântica e as descrições clássicas [5, 22, 24, 26]. Conforme o tamanho das nanopartículas diminui, a ressonância do plasmon muda para energias mais altas com desvio visível das previsões clássicas [5, 21, 22]. Além disso, as propriedades dinâmicas de NCs altamente dopados passam por uma transição do regime de quantização por tamanho para o regime clássico de oscilações de plasmon [22]. Isso pode ser observado variando o número de transportadoras ou o tamanho do NC.

Neste trabalho, apresentamos uma análise teórica da resposta óptica de NCs ZnO fotodopados tal como investigado experimentalmente na Ref. [21, 27]. Nestes estudos experimentais, as seções transversais de fotoabsorção de ZnO NC coloidal de tamanhos fixos e densidades de portadores foram medidas. Os fotoelétrons da banda de condução foram gerados no ZnO NC pelo processo de fotodopagem, enquanto os buracos foram presos pelos centros de eliminação de buracos no tolueno circundante. A concentração média de elétrons condutores n _e em nanocristais fotodopados quase esféricos de raios diferentes (de 1,75 a 6 nm) atingiu um limite superior de (1,4 ± 0,4) × 10 ²⁰ cm ⁻³ [21, 27]. A absorbância intrabanda foi medida na faixa de 0,2 a 1,0 eV, e diferenças significativas com a predição do modelo clássico de Drude foram observadas. Os autores mostraram que uma abordagem mecânica quântica baseada em transições de partícula única rendeu a dependência do tamanho experimental da frequência de ressonância apenas qualitativamente [21].

O objetivo deste artigo é revisitar a abordagem teórica das ressonâncias plasmônicas em ZnO NCs fotodopados, indo além da aproximação de partícula única não-interagente [21, 27]. É baseado no tratamento mecânico quântico autoconsistente de muitos corpos de elétrons de condução dentro da aproximação de fase aleatória (RPA) com troca local [28]. Foi mostrado que portadores de carga livre em nanopartículas semicondutoras formam conchas semelhantes a atômicas [29, 30]. Resolvemos as equações de Kohn-Sham da aproximação de densidade local (LDA) para descrever a estrutura da camada de elétrons. As correlações de elétrons responsáveis pelas excitações coletivas do plasmon são levadas em consideração dentro do RPA. Mostramos que a ressonância de plasmon em ZnO NC difere substancialmente da bem conhecida ressonância de Mie em gotículas metálicas. Em variação com NCs dopados semelhantes a bulk, não há restauração de carga positiva em NCs dopados semelhantes a superfície. Conseqüentemente, a repulsão de Coulomb entre os elétrons livres os empurra para perto da superfície NC. Por sua vez, esta configuração eletrônica específica leva a um modo dipolo, onde apenas os graus de liberdade angulares são excitados, enquanto o movimento radial eletrônico não está envolvido. Ao contrário do plasmon dipolo de superfície Mie comum, onde os elétrons sofrem oscilações translacionais puras, os elétrons em ZnO NCs altamente dopados sofrem vibrações tangenciais dentro da casca eletrônica bastante fina de uma maneira semelhante às oscilações do plasmon nas moléculas de fulereno [31]. Também mostramos que a transição desse modo de plasmon do regime de confinamento clássico para o quântico é governada pela razão entre o tamanho do NC e o raio de Bohr efetivo e não depende do número de elétrons livres. Os efeitos quânticos nas oscilações do plasmon resultam em um desvio para o azul da frequência de ressonância dipolo que concorda perfeitamente com a dependência de tamanho LSPR experimentalmente observada [21].

Métodos

O objetivo do estudo é a análise teórica das propriedades ópticas de nanocristais de ZnO fotodopados. As configurações do estado fundamental dos sistemas com vários números de partículas foram calculadas dentro da aproximação da densidade local. As funções de onda do estado fundamental são energias de partícula única que foram obtidas por resolução numérica autoconsistente do conjunto de equações de Kohn-Sham [32]. A base completa dos estados de uma única partícula foi gerada usando o método B-spline [33], expandindo as funções de base em uma cavidade de grande raio sobre um número finito de B-splines. O raio da cavidade foi escolhido igual ao raio NC. A precisão desejada dos cálculos com o uso da base discreta B-spline foi alcançada pela escolha apropriada do número e da ordem dos B-splines usados no cálculo. Usamos 50 B-splines da ordem 7 para alcançar precisão suficiente (10 ⁻⁵ ) dos resultados. A sub-rotina padrão RG do pacote de sub-rotina do eigensystem (EISPACK) foi usada para a obtenção dos autovalores e dos autovetores da equação da matriz RPA [28], cuja solução nos fornece o conjunto de energias de excitação dipolo e as intensidades do oscilador correspondentes. O espectro de fotoabsorção foi obtido pelo alargamento da distribuição calculada da resistência à oscilação por perfis Lorentzianos com largura de dobragem fixa.

Resultados e discussão

Estrutura do estado fundamental

Consideramos o sistema de N elétrons da banda de condução localizados dentro do ZnO NC do raio R . Seguindo [21], assumimos que o número de elétrons varia com o tamanho do NC como N =4 π n _e R ³ / 3, onde a concentração média fixa de elétrons, n _e =1,4 × 10 ²⁰ cm ⁻³ , é determinado pelo nível mais alto alcançável no processo de fotodopagem. O raio dos NCs considerados varia de 2,4 a 6 nm; consequentemente, o número de elétrons de condução, N , variam de 8 a 128.

Empregamos a aproximação da função de envelope para descrever o movimento do elétron assumindo que R é muito maior do que a constante de rede. Sabe-se que a estrutura de banda eletrônica do bulk ZnO é caracterizada por um espectro de energia não isotrópico e não parabólico [34]. No entanto, para o problema atual de dinâmica coletiva de N elétrons deslocalizados, vamos negligenciar esses pequenos efeitos de espectro de energia e considerar uma dispersão de energia parabólica isotrópica com massa efetiva \ (m_ {e} ^ {*} =0,3 ~ m_ {e} \) [34]. Pelo mesmo motivo, consideramos os ZnO NCs como sistemas esféricos.

Como os elétrons estão fortemente localizados dentro do volume ZnO NC devido ao deslocamento da banda de alta condução na interface NC [6], impomos que todas as funções de onda de elétrons desapareçam na fronteira NC r = R . Assim, consideramos N elétrons em interação localizados dentro de um poço esférico infinito, cuja neutralidade de carga geral é garantida por uma distribuição de superfície de carga positiva que não cria nenhum campo dentro do NC. O hamiltoniano efetivo do sistema considerado é simplesmente:
$$ \ hat {H} =\ sum \ limits_ {a} \ frac {\ hat {\ mathbf {p}} ^ {2} _ {a}} {2 m_ {e} ^ {*}} + \ frac {1} {2} \ sum \ limits_ {a, b} V \ left (\ mathbf {r} _ {a}, \ mathbf {r} _ {b} \ right), $$ (1)
onde V ( r _a , r _b ) representa o par de interação de Coulomb de elétrons. Sua expressão explícita, responsável pela polarização do material ZnO e da mídia circundante, é escrita como uma expansão multipolar [3],
$$ \ begin {alinhados} &V \ left (\ mathbf {r} _ {a}, \ mathbf {r} _ {b} \ right) =\ sum \ limits_ {L, M} \ frac {4 \ pi V_ {L}} {2L + 1} Y_ {LM} (\ mathbf {n} _ {a}) Y ^ {*} _ {LM} (\ mathbf {n} _ {b}), \\ &V_ {L } =\ frac {e ^ {2}} {\ varepsilon_ {i}} \ left (\ frac {r ^ {L} _ <} {r ^ {L + 1} _>} + \ frac {\ left ( \ varepsilon_ {i} - \ varepsilon_ {m} \ right) \ left (L + 1 \ right) \ left (r_ {a} r_ {b} \ right) ^ {L}} {\ left (L \ varepsilon_ { i} + (L + 1) \ varepsilon_ {m} \ right) R ^ {2L + 1}} \ right), \ end {alinhado} $$ (2)
onde r _< e r _> são a menor e a maior das duas posições radiais, respectivamente. As constantes dielétricas de ZnO e tolueno recebem seus valores em massa ε _i =3.7 e ε _m =2,25 [21], respectivamente. Com esses parâmetros, o raio de Bohr efetivo \ (a_ {0} =\ hbar ^ {2} \ varepsilon _ {i} / m_ {e} ^ {*} e ^ {2} =0,65 \) nm é menor que o Raio NC.

As energias do elétron de partícula única, ε _i , e funções de onda de envelope ψ _i satisfazer o conjunto de equações LDA Kohn-Sham,
$$ \ left [\ frac {\ hat {\ mathbf {p}} ^ {2}} {2 m_ {e} ^ {*}} + V_ {mf} (\ mathbf {r}) \ right] ~ \ psi_ {i} (\ mathbf {r}) =\ epsilon_ {i} \ psi_ {i} (\ mathbf {r}), $$ (3)
onde o potencial de campo médio V _mf é dado pela soma de direto, V _D ( r ), e troca, V _x ( r ), peças,
$$ \ begin {alinhados} &V_ {mf} (\ mathbf {r}) =V_ {D} (\ mathbf {r}) + V_ {x} (\ mathbf {r}), \\ &V_ {D} ( \ mathbf {r}) =\ int V (\ mathbf {r}, \ mathbf {r} ^ {\ prime}) \ rho (\ mathbf {r} ^ {\ prime}) d \ mathbf {r} ^ { \ prime}, \ quad V_ {x} (\ mathbf {r}) =- \ frac {e ^ {2}} {\ varepsilon_ {i}} \ left (\ frac {3 \ rho (\ mathbf {r} )} {\ pi} \ right) ^ {1/3}, \ end {alinhado} $$ (4)
com \ (\ rho =\ sum _ {i} | \ psi _ {i} | ^ {2} \) sendo a densidade do elétron. Observe que poderíamos substituir o termo de troca dependente da densidade local em sua forma Dirac por um termo de correlação de troca dependente da densidade local mais realista, como normalmente feito. Não fazemos isso porque a construção teórica de estados excitados que se seguirão automaticamente explica uma grande parte das correlações de estado fundamental de natureza RPA.

Por uma questão de simplicidade, consideramos as configurações de elétrons esfericamente simétricos com camadas eletrônicas fechadas. Nesse caso, as funções de onda de partícula única são dadas como os produtos das componentes radial, angular e de spin [35]. Consequentemente, o índice i =( n , l ), onde n é o número quântico radial e l o momento angular um. A solução numérica da Eq. (3) para o número do elétron N <130 mostrou que a configuração eletrônica do estado fundamental era feita de estados eletrônicos ocupados com os números quânticos radiais mais baixos n =1. Esses estados eletrônicos têm funções de onda radial sem nós e diferem pelos valores dos momentos angulares l . Assim, levando em consideração a degeneração do spin, os números "mágicos" de elétrons para tais configurações simétricas são N =2 ( l _max +1) ² , onde l _max é o momento angular máximo do estado eletrônico mais ocupado. Na Fig. 1, mostramos as distribuições de densidade ρ ( r ) para o NC com N =18, 50, 128 elétrons. Pode-se ver que a distribuição da densidade radial se torna cada vez mais estreita e se desloca em direção à interface NC conforme o tamanho aumenta. O encarte da Fig. 1 mostra a dependência do tamanho do valor eletrônico médio da distribuição radial eletrônica 〈 r 〉 No raio NC R e a proporção δ r / R , de sua dispersão \ (\ delta r =\ sqrt {\ langle r ^ {2} \ rangle - {\ langle r \ rangle} ^ {2}} \) (que pode ser considerada como a largura efetiva do escudo eletrônico) para o raio NC. Esta proporção é de apenas ∼ 0,15 para o menor NC com N =8 elétrons diminui rapidamente para os sistemas maiores. Numericamente, a largura do escudo eletrônico δ r é cerca de dois terços do raio efetivo de Bohr a ₀ enquanto o pico da concha eletrônica é deslocado da interface NC devido à reflexão quântica em aproximadamente R - 〈 r 〉 ≃2 a ₀ . Esta característica do sistema eletrônico decorre da forte repulsão de Coulomb que empurra os elétrons para a fronteira NC formando uma distribuição de carga esférica oca. Se o raio do NC for grande o suficiente, a força de repulsão de Coulomb na fronteira do NC e ² N / ε _i R ² torna-se muito mais forte do que a força centrífuga \ (\ hbar ^ {2} l (l + 1) / m_ {e} ^ {*} {\ langle r \ rangle} ^ {3} \) mesmo para o estado mais ocupado com \ (l =l_ {max} =\ sqrt {N / 2} -1 \). Pode-se ver que sua proporção é de a ₀ / 2 R . É por isso que os movimentos radiais e angulares do elétron se separam se R ≫ a ₀ . Neste caso, o sistema eletrônico é semelhante a um rotador quântico, por exemplo, o espectro de energia de estados de partícula única ocupados ε _i da Eq. (3) é bem aproximado pela fórmula,
$$ \ epsilon_ {1, l} - \ epsilon_ {1,0} =\ frac {\ hbar ^ {2} l (l + 1)} {2m_ {e} ^ {*} {\ langle r \ rangle} ^ {2}}. $$ (5)

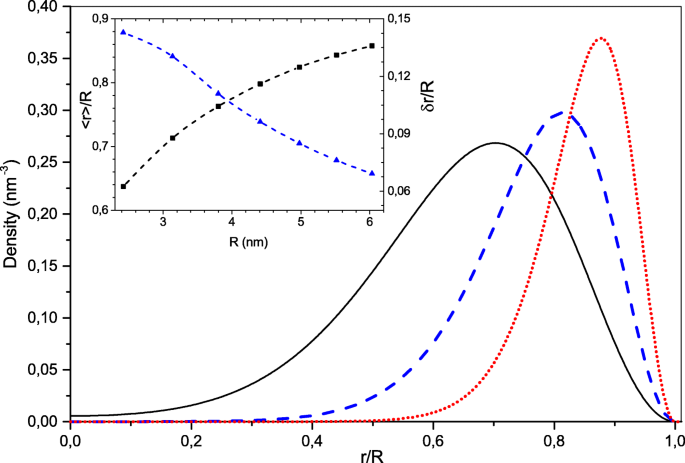
Distribuições de densidade radial para NCs com diferentes números de elétrons deslocalizados, N =18 (preto sólido como), 50 (linha azul tracejada), 128 (linha vermelha pontilhada). Na inserção, o raio médio reduzido (preto) e sua dispersão (azul) são representados como uma função do raio NC

Resposta óptica

Na aproximação de resposta linear, um campo elétrico harmônico externo induz campos autoconsistentes dependentes do tempo de mesma frequência. O conhecimento das vibrações de pequena amplitude correspondentes fornece informações sobre os estados excitados do dipolo, bem como sobre as probabilidades de transição entre o estado fundamental e os estados excitados. Para um sistema cujo estado fundamental é um determinante de Slater | Φ ₀>, os estados excitados dipolo de muitos corpos correlacionados dentro da abordagem RPA são construídos como uma superposição linear de uma excitação partícula-buraco [36]:
$$ | \ Phi _ {\ nu}> =\ sum_ {i> F, j . $$ (6)
Os índices i , m , ( j , n ) referem-se aos estados de partícula única acima (abaixo) do nível F de Fermi; \ (\ hat {a} ^ {+} \) e \ (\ hat {a} \) são os operadores de uma única partícula de criação e destruição, respectivamente.

As amplitudes para frente, \ (X_ {ij} ^ {\ nu} \), e para trás, \ (Y_ {ij} ^ {\ nu} \), podem ser obtidas resolvendo a equação matriz RPA [ 28]:
$$ \ left (\ begin {array} {ll} \ mathbf {A} &\ mathbf {B} \\ \ mathbf {B} ^ {\ star} &\ mathbf {A} ^ {\ star} \ end { array} \ right) \ left (\ begin {array} {l} \ mathbf {X} ^ {\ nu} \\ \ mathbf {Y} ^ {\ nu} \ end {array} \ right) =\ omega_ { \ nu} \ left (\ begin {array} {l} \ mathbf {X} ^ {\ nu} \\ - \ mathbf {Y} ^ {\ nu} \ end {array} \ right), $$ (7 )
onde os valores próprios ω _ν são as energias de excitação. As matrizes A e B são definidos como segue
$$ {\ begin {alinhados} A_ {ij, mn} &\, =\, \ delta_ {im} \ delta_ {jn} \ left (\ varejpsilon_ {i} - \ varejpsilon_ {j} \ right) \, + \, \ left \ langle in \ left | \ hat {v} \ right | jm \ right \ rangle, \ quad B_ {ij, mn} &\, =\, \ left \ langle im \ left | \ hat {v} \ right | jn \ right \ rangle \\ \ hat {v} (\ mathbf {r}, \ mathbf {r} ^ {\ prime}) &=V (\ mathbf {r}, \ mathbf {r} ^ {\ prime} ) + \ delta \ left (\ mathbf {r} - \ mathbf {r} ^ {\ prime} \ right) \ delta V_ {x} / \ delta \ rho. \ end {alinhado}} $$ (8)
Observe de passagem que as amplitudes para trás, \ (Y_ {ij} ^ {\ nu} \), medem a contribuição das correlações do estado fundamental do buraco do elétron \ (\ hat {a} _ {j} ^ {+} \ hat { a} _ {i} | \ Phi _ {0}> \), respectivamente, à excitação do estado excitado | Φ _ν> de frequência ω _ν .

As forças do oscilador dipolo correspondentes f _ν são expressos em termos de amplitudes RPA X ^ν e Y ^ν ,
$$ f _ {\ nu} =\ frac {2 m_ {e} ^ {*} D ^ {2} _ {\ nu} \ omega _ {\ nu}} {\ hbar ^ {2}}, \ quad D_ { \ nu} =\ sum_ {ij} \ left (X ^ {(\ nu)} _ {ij} d_ {ij} + Y ^ {(\ nu)} _ {ij} d_ {ji} \ right), $ $ (9)
onde d _ij =〈 i | z | j 〉 São os elementos da matriz dipolo de partícula única.

As seções transversais de fotoabsorção foram obtidas ampliando a distribuição calculada da resistência do oscilador por perfis Lorentzianos com largura de dobramento de 0,2 ω . Espectros de fotoabsorção juntamente com distribuições de força do oscilador para NCs com N =8 (a), 32 (b), 50 (c) e 128 (d) elétrons são mostrados na Fig. 2. Na Fig. 2d, comparamos a seção transversal de fotoabsorção calculada com os dados experimentais da Ref. [21] para ZnO NC com R ≃ 6 nm. Pode-se observar que em todas as NCs consideradas, os espectros são dominados por uma única linha de ressonância, cuja posição na verdade determina o máximo da seção de choque de fotoabsorção. Na verdade, isso é esperado, uma vez que o espectro eletrônico de partícula única é semelhante a um rotador quântico. As transições mais fortes acontecem para uma função de onda máxima sobreposta, ou seja, com número quântico radial igual n . Em nosso caso, há apenas uma transição óptica do estado mais ocupado j =(1, l _max ) para o estado vago mais baixo i =(1, l _max +1). No entanto, a excitação dipolo correspondente difere fortemente da transição de partícula única sem interação sempre que uma forte repulsão de Coulomb torna as correlações de elétrons importantes e opressivas. Este é o caso quando R ≫ a ₀ . Ou seja, a energia da excitação coletiva, ω _ν , excede a energia de transição de partícula única
$$ \ Delta =\ left (\ epsilon_ {1, l_ {max} +1} - \ epsilon_ {1, l_ {max}} \ right) =\ frac {\ hbar ^ {2} (l_ {max} + 1)} {m_ {e} ^ {*} {\ langle r \ rangle} ^ {2}}. $$ (10)

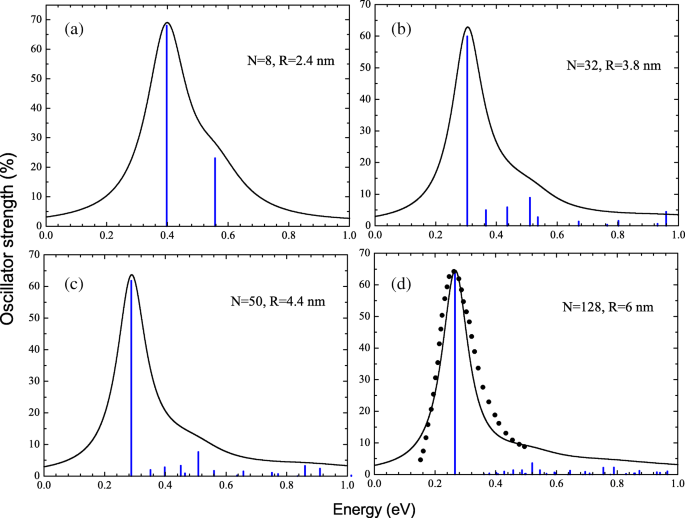
Distribuições de força do oscilador e perfis de pico de fotoabsorção correspondentes calculados dentro da abordagem RPAE para NCs com N =8 ( a ), 32 ( b ), 50 ( c ), e 128 ( d ) elétrons da banda de condução. Comparação de perfis de pico de ressonância experimentais [21] (quadrados pretos) e calculados (linha sólida) para NC com R ≈6 nm ( d )

Na Fig. 3, comparamos as posições dos máximos de fotoabsorção, ω _res , calculado aqui (círculos azuis) com resultados experimentais de [21] (estrelas vermelhas). Observa-se uma notável concordância entre os dados experimentais e nossos resultados teóricos. Para comparação, também plotamos aqui as energias Δ de transição de partícula única (quadrados verdes). As correlações de elétrons aumentam consideravelmente a energia de excitação coletiva comparativamente a Δ . Uma análise simples de RPA Eq. (7) explica esta observação. Se considerarmos apenas a transição óptica principal de j =(1, l _max ) para j =(1, l _max +1) afirma, o RPA Eq. (7) se reduz a uma equação de matriz 2 × 2, cujo autovalor ω e simples:
$$ \ omega ^ {2} =\ Delta ^ {2} + 2V \ Delta, $$ (11)

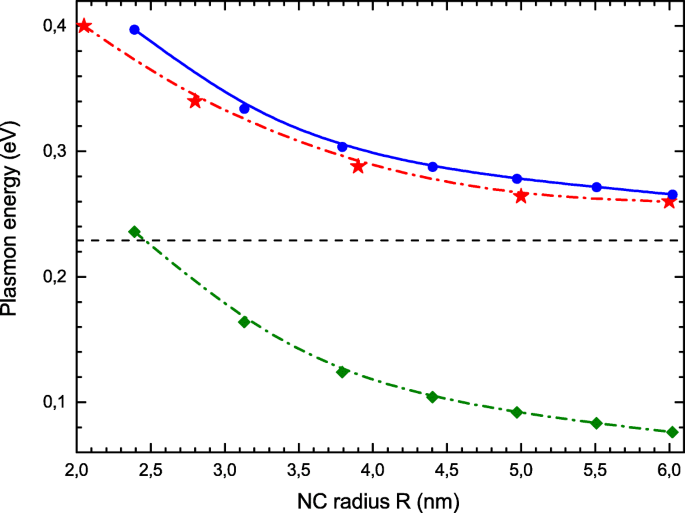
Dependência do tamanho da energia LSPR. Valores experimentais [21] (estrelas vermelhas), RPA com troca local (círculos azuis), energias de transição de partícula única (diamantes verdes na curva inferior). O valor clássico (13) é mostrado pela linha tracejada horizontal

onde \ (V =\ left \ langle ij \ left | \ hat {v} \ right | ij \ right \ rangle \) denota o elemento da matriz RPA Coulomb. O primeiro termo da r.h.s. da Eq. (11) fornece a contribuição de uma única partícula, enquanto o segundo termo resulta das interações partícula-orifício. Sua razão pode ser estimada tomando a coordenada radial do elétron na superfície, r = R no elemento da matriz RPA V , e negligenciando o termo de troca. Esta estimativa produz
$$ \ frac {2V} {\ Delta} \ simeq \ frac {4R \ varepsilon_ {i}} {a_ {0} (\ varepsilon_ {i} +2 \ varepsilon_ {m})} \ simeq \ frac {2R} {a_ {0}}. $$ (12)
Assim, a contribuição das correlações eletrônicas domina se R ≫ a ₀ . No limite de grandes NCs, a distribuição da densidade de elétrons concentra-se na superfície do NC; portanto, de acordo com a Eq. (12), a energia de ressonância na Eq. (11) tende a
$$ \ omega =\ sqrt {\ frac {2 \ hbar ^ {2} e ^ {2} N} {m_ {e} ^ {*} (\ varepsilon_ {i} +2 \ varejpsilon_ {m}) R ^ {3}}}, $$ (13)
que coincide exatamente com a frequência de dipolo plasmon clássico em fina concha esférica [37]. Este modo plasmon corresponde a uma vibração eletrônica tangencial. Desta forma, é semelhante à ressonância de plasmon de superfície em C ₆₀ moléculas, onde a frequência de ressonância é bem descrita pela equação análoga à Eq. (13) [38]. Observe que, como o caso do fulereno [39], este modo de plasmon reúne dois terços da força de oscilação total (ver Fig. 2). Isso ocorre porque essa oscilação envolve apenas os graus de liberdade angulares, mantendo o movimento radial inalterado.

Ao contrário do conhecido modo de plasmon de superfície dipolo em esferas homogêneas, que é puramente translacional, o modo da presente consideração é compressional. A densidade induzida produz um campo elétrico paralelo à superfície que desempenha o papel de restaurar a força para este modo plasmon. Além disso, a variação puramente quântica do nível de Fermi local devido às oscilações de densidade induzidas contribui para a força de restauração. A contribuição da pressão quântica correspondente para a frequência de ressonância é dada pelo Δ termo na Eq. (11). É menor do que a contribuição de Coulomb em todos os NCs considerados devido à pequenez do raio efetivo de Bohr a ₀ em ZnO. Porém, em NCs com maior valor de a ₀ , pode-se observar a transição da ressonância de plasmão dipolo clássico para o regime de confinamento quântico em R ∼ a ₀ . Vale ressaltar que no caso de NCs dopados, o parâmetro a ₀ / R que controla a natureza clássica / quântica da ressonância dipolo depende apenas do tamanho do NC e não depende do número de portadores livres N .

Na Fig. 3, a linha horizontal refere-se à clássica energia de ressonância do plasmão (13). O deslocamento para o azul da frequência de ressonância em relação ao seu valor clássico é causado por dois efeitos quânticos, a contribuição da pressão quântica discutida acima e a diminuição do raio médio do elétron. O último acontece porque os elétrons são empurrados no volume NC devido à reflexão quântica da fronteira, de modo que 〈 r 〉 ≃ R -2 a ₀ . Este efeito aumenta o elemento da matriz V que por sua vez aumenta a frequência de ressonância. Grosso modo, este efeito pode ser reproduzido substituindo o raio NC R no denominador da Eq. (13) por 〈 r 〉. De acordo com as Eqs. (11) - (13), ambos os efeitos fornecem a mudança de frequência do azul proporcional ao raio NC inverso ∝1 / R . Porém, numericamente, a contribuição deste último é a maior.

Conclusões

Para concluir esta carta, elaboramos uma teoria que prevê muito bem a forte ressonância dipolo observada em NCs coloidais de ZnO altamente dopados com n. O novo tipo de excitações de plasmão dipolo de superfície foi teoricamente estudado usando a abordagem quântica de muitos corpos. Demonstramos que a forte repulsão de Coulomb em nanocristais de ZnO fotodopados leva a uma distribuição de elétrons de estado fundamental específico localizada em uma fina camada superficial próxima à superfície interna. Quando o dipolo é excitado, essa distribuição eletrônica sustenta uma oscilação plasmônica coletiva que é essencialmente formada por movimento angular. A transição desse modo de plasma de superfície do regime de confinamento clássico para o quântico é governada por um único parâmetro igual à razão do tamanho do nanocristal para o raio de Bohr efetivo. A reflexão de elétrons da interface NC reduz o raio do invólucro eletrônico. Além disso, a variação do nível de Fermi local dá uma contribuição adicional para a força de restauração do oscilador de plasmon. Esses efeitos quânticos levam à dependência do tamanho da frequência de ressonância do plasmon, o que é uma concordância notável com as observações experimentais. No limite de um grande raio NC, a linha de ressonância tende suavemente para a frequência plasmônica clássica de uma concha carregada de largura infinitesimal.

Abreviações

LDA:: Aproximação de densidade local
LSPR:: Ressonância de plasmon de superfície localizada
NC:: Nanocristal
RPA:: Aproximação de fase aleatória

Efeito da dispersão superficial de elétrons nas proporções de absorção óptica e dispersão para extinção de nanoconcha de ouro Detecção rápida de rongalita por meio de um ensaio de faixa de fluxo lateral sanduíche usando um par de aptâmeros

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias