Modulação aprimorada de ressonância acoplada para um absorvedor de metamaterial carregado com grafeno

Resumo

Um absorvedor de metamaterial carregado com grafeno é investigado na região do infravermelho médio. A interação luz-grafeno é bastante reforçada em virtude da ressonância acoplada através de uma fenda em forma de cruz. Os picos de absorção mostram um blueshift significativo com o aumento do nível de Fermi, permitindo uma ampla gama de sintonia para o absorvedor. Um modelo de circuito simples explica e prevê bem esse comportamento de modulação. Nossa proposta pode encontrar aplicações em uma variedade de áreas, como comutação, detecção, modulação e detecção bioquímica.

Histórico

Os absorvedores de metamaterial plasmático (PM) trabalham com nanoestruturas metálicas em uma escala profunda de comprimento de onda. Absorções perfeitas podem ser alcançadas e ajustadas em comprimentos de onda específicos, levando a uma variedade de aplicações, incluindo emissor / detector de luz, sensor, terapia fototérmica, interação ótico-mecânica e imagem hiperespectral [1,2,3,4,5,6,7 ] Os absorvedores de PM também fornecem uma plataforma promissora para projetar novos dispositivos funcionais com propriedades ajustáveis. Ao introduzir componentes como cristais líquidos, semicondutores ou materiais de mudança de fase, a resposta óptica pode ser modulada eletricamente, opticamente ou termicamente [8,9,10,11,12,13], o que permite novos tipos de moduladores, interruptores e detectores multiespectrais.

Mais recentemente, o grafeno tem recebido atenção considerável por causa de sua capacidade de modulação de alta velocidade e sintonia como um material plasmônico [14,15,16,17,18,19,20]. Especificamente, a condutividade do grafeno depende do nível de Fermi ( E _F ), que pode ser continuamente sintonizado através da tensão de polarização dentro de vários nanossegundos, permitindo uma alta taxa de modulação nas regiões do infravermelho próximo e infravermelho médio [17, 19,20,21,22,23,24]. No entanto, como a única camada de grafeno é apenas atomicamente espessa, a interação entre a luz incidente e a ressonância plasmônica é bastante fraca. E essa interação torna-se ainda mais fraca na área do infravermelho médio devido ao bloqueio de Pauli das transições entre bandas [22]. Como resultado, a faixa de sintonia do comprimento de onda, bem como a profundidade da modulação, são bastante limitadas. O deslocamento do comprimento de onda é geralmente menor que 10% do comprimento de onda de ressonância [21, 22, 25,26,27,28], o que ainda é um desafio para aplicações práticas em comunicações ópticas e detecções espectrais de banda larga. Assim, a fim de alcançar uma modulação eletro-óptica eficiente, a interação grafeno-luz precisa ser muito fortalecida. Alguns avanços foram feitos em estudos anteriores. Com base nos projetos de nanoestruturas complexas, como nanoantenas e ressonadores de anel dividido [19, 21, 22, 25, 27, 28], o aprimoramento da interação grafeno-luz foi demonstrado teórica e experimentalmente. No entanto, esses projetos são geralmente complicados ou dependentes da polarização, a faixa de frequência de trabalho é relativamente pequena e a sintonização ainda é limitada.

Neste trabalho, propusemos um absorvedor carregado de grafeno com faixa de modulação de 9 a 14 μm, que é de grande interesse para aplicações como sensoriamento bioquímico e imagens térmicas [5, 29,30,31]. As ressonâncias acopladas dentro da fenda em forma de cruz oferecem quatro ordens de realce para o campo elétrico, intensificando fortemente a interação grafeno-luz e resultando em um deslocamento de até 25% no comprimento de onda central. Além disso, propomos um modelo de circuito LC simples que explica e prevê bem a modulação induzida pelo grafeno controlada pela tensão e parâmetros geométricos. Uma gama tão grande de sintonia seria promissora em muitas aplicações.

Métodos

Como mostrado na Fig. 1a, remendos metálicos padronizados são arranjados com um período de Λ =8 μm no substrato de metal separados por um espaçador dielétrico. Uma única camada de sanduíches de grafeno entre os remendos e o espaçador. O substrato é muito espesso e atua como um espelho de reflexão. A espessura da camada espaçadora é t _d =520 nm e o dos remendos metálicos é t _m =100 nm. A Figura 1b mostra a vista superior de uma célula unitária. Duas subunidades são organizadas em uma simetria diagonal para apoiar a independência de polarização. Uma fenda em forma de cruz é gravada em cada remendo quadrado, dividindo-o em quatro pequenos idênticos. Os tamanhos dos pequenos idênticos em S ₁ e S ₂ são l ₁ =1,5 μm e l ₂ =1,7 μm, respectivamente. A largura do slot para ambas as subunidades é a =20 nm. Em nosso estudo, o material metálico é escolhido como ouro (Au), cuja propriedade ótica é descrita pelo modelo Drude de \ (\ varejpsilon \ left (\ omega \ right) =1 - {\ omega} _p ^ 2 / \ left (\ omega \ left (\ omega + \ tau \ right) \ right) \) com ω _p =1,369 × 10 ¹⁶ Hz e τ =1,224 × 10 ¹⁴ Hz [32]. O espaçador dielétrico é composto por sulfeto de zinco (ZnS), cujo índice óptico é n =2,2 com perda desprezível na região do infravermelho médio [33].

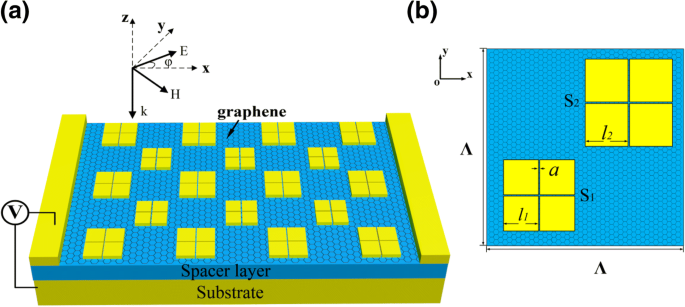
a Diagrama esquemático do metamaterial carregado de grafeno proposto. A fenda em forma de cruz em cada subunidade permite um grande aprimoramento da interação grafeno-luz sem dependência de polarização. b Vista superior da estrutura em um período. Duas subunidades são organizadas diagonalmente com tamanhos de remendo diferentes

O método de domínio de tempo de diferença finita (FDTD; Lumerical FDTD Solutions) é empregado para calcular espectros de refletância e distribuição de campo eletromagnético. As simulações são realizadas com condições de contorno periódicas no x e y direções e condições de camada correspondentes perfeitas no z instruções. A única camada de grafeno é modelada como uma estrutura bidimensional pela abordagem da condutividade de superfície [34]. A condutividade da superfície da camada de grafeno σ _g , incluindo o termo entre bandas σ _inter e o termo intrabanda σ _intra , pode ser calculado pela fórmula de Kubo [35].
$$ {\ displaystyle \ begin {array} {l} {\ sigma} _ {\ mathrm {g}} \ left (\ omega, {E} _ {\ mathrm {F}}, \ Gamma, T \ right) ={\ sigma} _ {\ mathrm {intra}} + {\ sigma} _ {\ mathrm {inter}} \\ {} =\ frac {- {ie} ^ 2} {\ pi {\ mathrm {\ hslash }} ^ 2 \ left (\ omega + i2 \ Gamma \ right)} \ underset {0} {\ overset {\ infty} {\ int}} \ xi \ left (\ frac {\ partial {f} _d \ left (\ xi \ right)} {\ partial \ xi} - \ frac {\ partial {f} _d \ left (- \ xi \ right)} {\ partial \ xi} \ right) d \ xi + \ frac {ie ^ 2 \ left (\ omega + i2 \ Gamma \ right)} {\ pi {\ mathrm {\ hslash}} ^ 2} \ underset {0} {\ overset {\ infty} {\ int}} \ xi \ left (\ frac {f_d \ left (- \ xi \ right) - {f} _d \ left (\ xi \ right)} {{\ left (\ omega + i2 \ Gamma \ right)} ^ 2-4 {\ left (\ xi / \ mathrm {\ hslash} \ right)} ^ 2} \ right) d \ xi \ end {array}} $$ (1)
onde e e ξ são a carga e a energia do elétron, ℏ é a constante da prancha reduzida, ω é a frequência angular, \ ({f} _d \ equiv 1 / \ left ({e} ^ {\ left (\ xi - {E} _F \ right) / {k} _BT} +1 \ right) \) refere-se para a distribuição Fermi-Dirac, T é a temperatura absoluta, Γ é a taxa de dispersão, k _B é a constante de Boltzmann, e E _F é o nível de Fermi. Em nosso cálculo, T =300 K, e Γ =10 meV [28]. O tamanho da malha perto da camada de grafeno é de 0,25 nm e 2,5 nm nas ranhuras. A permissividade efetiva do grafeno pode então ser expressa como
$$ {\ varejpsilon} _ {\ mathrm {g}} =1+ \ mathrm {i} {\ sigma} _ {\ mathrm {g}} / \ left ({\ varejpsilon} _0 \ omega {t} _ { \ mathrm {g}} \ right) $$ (2)
onde ε ₀ é a permissividade do vácuo, e t _g é a espessura da camada de grafeno. As equações (1) e (2) demonstram que as constantes ópticas do grafeno mudam com E _F . Essa mudança leva à sintonia da frequência de absorção, cujo alcance pode ser bastante ampliado pela ressonância acoplada nas nanoestruturas, diminuindo substancialmente a voltagem aplicada nos dispositivos.

Resultados e discussão

A Figura 2a mostra os espectros de absorção para x onda polarizada ( φ =0) na incidência normal. Quando o nível de Fermi é E _F =0eV, dois picos de absorção são observados no comprimento de onda λ =12,4 μm e 13,3 μm, respectivamente. A luz incidente variando de 12,1 a 13,5 μm é quase absorvida pela nanoestrutura. Como E _F aumenta, a ressonância se move em direção a um comprimento de onda mais curto. Em E _F =0,2 eV, os picos de absorção mudam para 11,8 μm e 12,46 μm, indicando respectivamente uma mudança relativa de 4,8% e 6%. Enquanto isso, a absorbância do pico 2 diminui, o que é atribuído à incompatibilidade de impedância entre o metamaterial e o ar em um E superior _F [28]. Aqui, é interessante que o pico 2 muda mais rapidamente do que o pico 1 à medida que o nível de Fermi continua aumentando. Este comportamento observado será explicado posteriormente por um modelo de circuito.

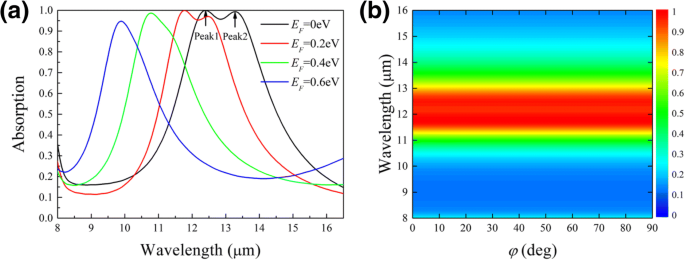
Espectros de absorção na incidência normal com diferentes E _F em φ =0, mostrando um grande blueshift dos picos com o aumento de E _F ( a ), e com diferentes φ em E _F =0,2eV, demonstrando uma independência de polarização ( b ) O ângulo de polarização φ é definido como na Fig. 1a

A modulação pode ser quantificada por um parâmetro M =Δ λ / λ ₀ , onde λ ₀ é o comprimento de onda de ressonância em E _F =0 eV e Δ λ é a mudança do comprimento de onda devido à mudança de E _F . A Figura 2a mostra M ₁ =20,1% e M ₂ =25,5% para o pico 1 e pico 2, respectivamente, quando E _F atinge 0,6 eV. A faixa de modulação das ressonâncias é muito mais ampla em comparação com trabalhos anteriores [19, 21, 22, 25,26,27,28]. Uma modulação tão grande em um E baixo _F é altamente desejável para muitas aplicações. Cálculos separados mostram que os picos de absorção mudam para o azul com a diminuição da espessura do espaçador (arquivo adicional 1). Assim, podemos otimizar a espessura para definir um ponto de início de modulação adequado. Além disso, a resposta óptica do metamaterial proposto é independente da polarização, conforme mostrado na Fig. 2b. O espectro de absorção permanece inalterado quando o ângulo de polarização φ varia de 0 a 90 °, devido à simetria do desenho.

O mecanismo de absorção perfeita é claramente ilustrado pelas distribuições de campo nas ressonâncias. Por causa da conhecida estrutura metal-isolante-metal (MIM) [3, 32, 36,37,38] mostrada na Fig. 1, SPPs localizados são estimulados para formar ressonâncias magnéticas compactas em cada patch. As Figuras 3a eb demonstram o campo magnético normalizado | H | ² na camada de grafeno para E _F =0,2 eV nos comprimentos de onda de ressonância de λ ₁ =11,8 μm e λ ₂ =12,46 μm, respectivamente. Como os SPPs são fortemente localizados, duas subunidades podem funcionar independentemente. No entanto, devido à largura estreita da fenda de divisão dentro de cada subunidade, as ressonâncias dos quatro idênticos são realmente acopladas umas às outras. E este acoplamento aumenta tremendamente o campo elétrico dentro do slot, como mostrado nas Fig. 3c e d. Apenas o E campos no y - os slots de direção são óbvios aqui porque a luz incidente está no x polarização. A intensidade do E campo realçado pelo acoplamento de ressonância é quatro ordens de magnitude maior do que o da luz incidente E _inc . Em contraste, os campos mais intensificados usados para modulação em trabalhos anteriores estão nas bordas do patch. As Figuras 3e e f mostram a comparação nítida dos realces entre as ranhuras e bordas ao longo da linha branca na Fig. 3c e d, respectivamente.

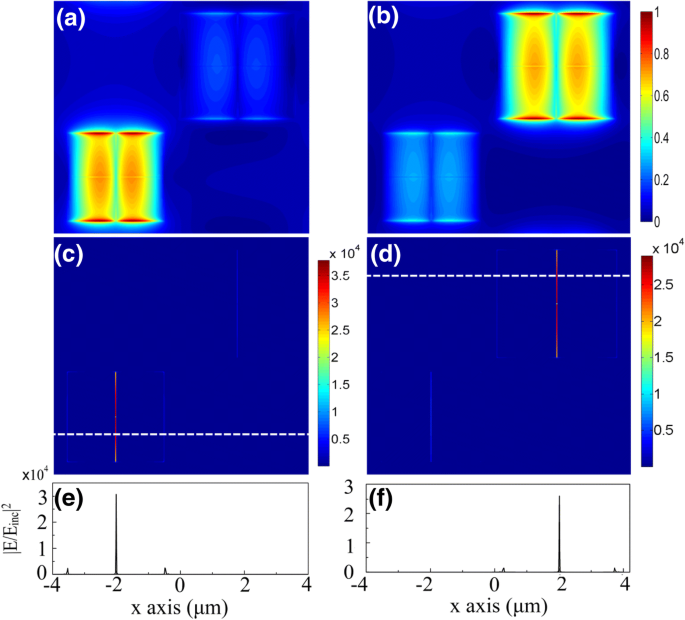
Distribuições de campo na camada de grafeno em E _F =0,2 eV para a luz x-polarizada na incidência normal, mostrando grande realce no slot causado pelas ressonâncias acopladas. a, b Campo magnético normalizado | H | ² em λ ₁ =11,8 μm ( a ) e λ ₂ =12,46 μm ( b ); c , d A distribuição de campo correspondente de | E / E _inc | ² ; e , f | E / E _inc | ² ao longo da linha de traço branca mostrada em c e d , respectivamente. Um contraste nítido é visto entre a intensidade dentro do slot e aquela nas bordas do patch, dando dicas para uma faixa de ajuste muito mais ampla do que em trabalhos anteriores

Tais distribuições de campo explicam bem a razão pela qual a modulação é tão grande em nossa proposta. Com base em uma teoria de perturbação, o deslocamento de ressonância induzido pelo grafeno pode ser avaliado como Δ ω =- iσ _g ∫ _S | E _s | ² dS / W ₀ [22]. Aqui, | E _s | ² é a intensidade do campo elétrico na camada de grafeno, W ₀ é a energia armazenada, e S denota a área coberta pelo grafeno. O deslocamento espectral da ressonância (Re (Δ ω )) é decidido pela parte imaginária de σ _g , que é muito maior do que sua parte real na região do infravermelho médio [22, 28]. Como mostrado claramente na Fig. 3c-f, o aumento do campo elétrico dentro da fenda estreita é mais de 10 vezes maior do que nas bordas. Como resultado, o valor integral é principalmente contribuído pelo altamente aprimorado E campo nos slots de patch, levando a uma mudança muito maior dos picos do que em casos anteriores que possuem apenas o E aprimorado campos nas bordas metálicas [21, 22, 25, 27, 28].

De acordo com as distribuições de campo e as discussões acima, um modelo de circuito LC é proposto para estudar o comportamento de sintonia. Conforme mostrado na Fig. 4a, L _i e C _i ( eu =1, 2) são, respectivamente, a indutância e a capacitância para o patch S _i na Fig. 1b. Quando a largura do slot a é muito grande e não há camada de grafeno, podemos ignorar os efeitos induzidos pelos slots e grafeno. Então, L _i e C _i pode ser decidido por cálculos separados através do ajuste com o comprimento de onda ressonante obtido no espectro de absorção [37, 39, 40]. Os resultados são L ₁ =0,07 pH e C ₁ =350 aF para a subunidade S ₁ , enquanto L ₂ =0,075 pH e C ₂ =380 aF para a subunidade S ₂ . O efeito de acoplamento induzido por slot dentro de cada subunidade pode ser descrito por uma capacitância shunt C _c , que diminui com o aumento da largura do slot a . Em nossos casos, C _c é 290 aF para a =20 nm, e se torna 200 aF, 180 aF e 135 aF com cada aumento de 10 nm de a . O comprimento de onda de ressonância é obtido deixando a impedância do circuito ser zero, ou seja, \ ({\ lambda} _i ^ 0 =2 \ pi {c} _0 \ sqrt {L_i {\ mathrm {C}} _ i ^ 0} \). Aqui, c ₀ é a velocidade da luz no vácuo, “ i ”Refere-se à subunidade S _i , e \ ({C} _i ^ 0 ={C} _i + {C} _c \).

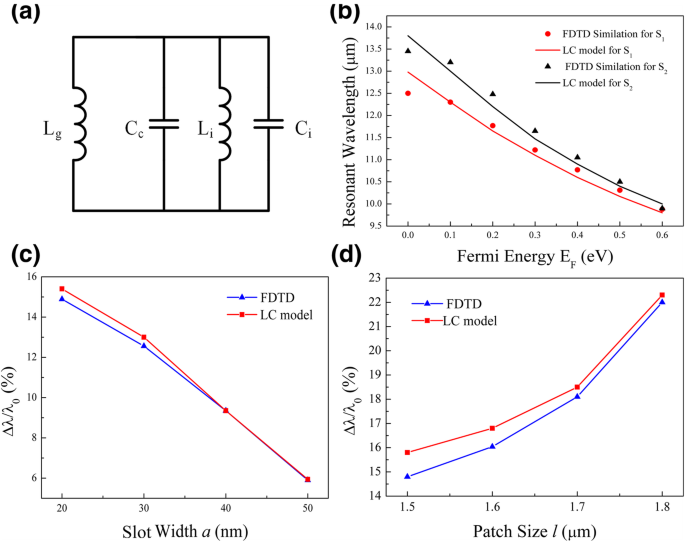
a Um modelo de circuito LC inclui contribuições de patches separados ( L _i e C _i ), slot ( C _c ) e grafeno ( L _g ) b Ressonâncias calculadas pelo modelo LC em comparação com simulações FDTD. c , d Mudança de ressonância para um único patch em E _F =0,4 eV com alteração do parâmetro geométrico de c largura do slot ( l =1,5 μm) e d tamanho do patch ( a =20 nm)

A camada de grafeno bidimensional basicamente atua como um indutor. Conforme mostrado na Fig. 3, a principal contribuição da camada de grafeno vem da posição da fenda onde o campo elétrico é intensificado. Uma vez que a largura da fenda é muito menor do que o comprimento de onda operacional e o comprimento de onda do plasmon grafeno, a aproximação quase estática é válida. A tensão V e o atual eu em todo o slot pode ser avaliado por V = aE e eu =2 l _i t _g ( σ _g - iωε ₀ ) E , onde E é o campo elétrico na camada de grafeno. Portanto, podemos introduzir uma indutância L _g =- 1 / ω Im (V / I) [41], que descreve a contribuição da camada de grafeno e é encontrado para ser
$$ {L} _ {\ mathrm varej {g}} =\ frac {a} {2 {l} _i {\ omega} ^ 2 {\ varepsilon} _0 \ left | \ operatorname {Re} \ left ({\ psilon } _ {\ mathrm {g}} \ right) \ right | {t} _ {\ mathrm {g}}} \ kern0.5em \ left (i =1,2 \ right) $$ (3)
Este indutor serve como um elemento paralelo mostrado na Fig. 4a. Como resultado, a indutância total de um patch é obtida por \ (1 / {L} _i ^ {\ prime} =1 / {L} _i + 1 / {L} _ {\ mathrm {g}} \). O comprimento de onda de ressonância final de cada subunidade, com a camada de grafeno, torna-se
$$ {\ lambda} _i ^ {\ prime} =2 \ pi {c} _0 \ sqrt {L_i ^ {\ prime} {\ mathrm {C}} _ i ^ 0} \ kern0.5em \ left (i =1 , 2 \ direita) $$ (4)
Como cada subunidade funciona de forma independente, a impedância total do metamaterial pode ser obtida a partir da conexão paralela das impedâncias das duas subunidades.

Este modelo LC prevê um blueshift da ressonância com o aumento de E _F . Deduzido das Eqs. (1) e (2), obtemos um valor maior de | Re ( ε _g ) | para o grafeno em um E superior _F , o que dá um menor L _g na Eq. (3). Por causa da conexão paralela dos indutores, o indutor final \ ({L} _i ^ {\ prime} \) torna-se menor, levando a um comprimento de onda de ressonância mais curto na Eq. (4). O resultado calculado está resumido na Fig. 4b, mostrando uma boa concordância com o comprimento de onda ressonante obtido pelas simulações FDTD. Um pequeno desvio é visto porque nosso modelo LC ignora a contribuição de campos fracos nas bordas de cada patch (Fig. 3c – f). O modelo LC também mostra como os parâmetros geométricos influenciam o blueshift da ressonância. Diferenciando a Eq. (4), temos \ (\ partial {\ lambda} _i ^ {\ prime} / \ partial {L} _i ^ {\ prime} \ propto 1 / \ sqrt {L_i ^ {\ prime}} \). É óbvio que um pequeno valor de \ (\ sqrt {L_i ^ {\ prime}} \) é preferido para aumentar a sensibilidade deste blueshift. Porque os indutores estão conectados paralelamente e L _i é fixo, um pequeno valor da indutância total \ ({L} _i ^ {\ prime} \) significa um pequeno valor da indutância de grafeno L _g . A fim de aumentar o intervalo de sintonia, a largura da ranhura a deve ser pequeno e o tamanho do patch l ser grande, de acordo com a Eq. (3). A Figura 4c mostra que o blueshift da ressonância em E _F =0,4 eV aumenta de cerca de 6 a 15%, quando a largura da ranhura dentro de S ₁ diminui de 50 para 20 nm. Por outro lado, se fixarmos a largura do slot em a =20 nm, a ressonância aumenta de 15 a 22% com o tamanho do patch mudando de 1,5 a 1,8 μm, conforme mostrado na Fig. 4d. A boa concordância com as simulações FDTD demonstra que tal modelo de circuito simples é um método eficiente para estudar dispositivos de metamateriais relacionados.

Conclusões

Em conclusão, projetamos um absorvedor de metamaterial de banda larga independente de polarização com uma grande faixa de modulação. Para ambas as ressonâncias, a faixa de sintonia atinge até 20,1% e 25,5% do comprimento de onda central quando E _F aumenta de 0 a 0,6 eV. Essa grande modulação vem da interação grafeno-luz tremendamente aprimorada pelas ressonâncias acopladas dentro da fenda em forma de cruz de cada remendo metálico. Este efeito é bem descrito por um indutor introduzido com grafeno no modelo LC. Esse modelo simples prevê o comportamento da modulação sob diferentes parâmetros geométricos e os resultados concordam bem com as simulações FDTD. Nossa proposta é benéfica para aplicações potenciais, como comunicação óptica, sensoriamento e geração de imagens térmicas.

Abreviações

E _F :: Nível de Fermi
FDTD:: Domínio do tempo finito diferente
MIM:: Metal-isolante-metal
PM:: Metamaterial plasmônico
ZnS:: Sulfeto de zinco

Uma referência de voltagem sem resistor de baixa potência em nanoescala com alto PSRR Medição e avaliação da temperatura da superfície local induzida pela irradiação de feixes de elétrons em escala nanométrica ou microescala

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias